Motor iónico
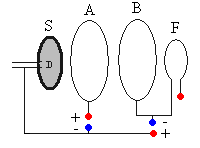
El propulsor se ioniza en la fuente de iones S y se expulsa como haz de iones positivos con una velocidad que depende de la diferencia de potencial V existente entre S y el anillo acelerador B. Para evitar que el cohete se cargue, se inyectan electrones en el haz mediante el filamento F. El haz se enfoca mediante el anillo A.
Sea dm/dt la masa del haz de partículas que salen de la fuente S en la unidad de tiempo, con una velocidad u respecto del cohete.
La fuerza de empuje es
Intensidad
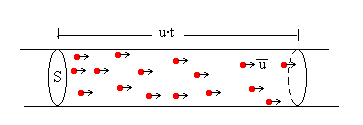
Sea n el número de partículas por unidad de volumen, u la velocidad media de dichas partículas, S la sección del haz y mp la masa de cada partícula.
La masa m de combustible expulsada en un tiempo t, es la contenida en un cilindro de sección S y longitud u·t.
Masa m= (número de partículas por unidad de volumen n)·(masa de cada partícula mp)· (volumen del cilindro Sut)
m=n·mp·S·u·t
por lo que
El flujo de masa, o masa que atraviesa la sección normal S en la unidad de tiempo, es el producto de los siguientes términos:
- Número de partículas por unidad de volumen, n
- La masa de cada partícula, mp.
- El área de la sección normal, S
- La velocidad media de las partículas, u.
De modo análogo, la intensidad I del haz, es el flujo de carga o la carga que atraviesa la sección normal S en la unidad de tiempo, será el producto de los siguientes términos:
- Número de partículas por unidad de volumen, n
- La carga de cada partícula, q.
- El área de la sección normal, S
- La velocidad media de las partículas, u.
I=nqSu
Expresamos la fuerza de empuje F en términos de la intensidad del haz de iones que salen de la fuente.
La velocidad con las que se mueven las partículas del haz depende de la diferencia de potencial acelerador V, entre la fuente S y el electrodo B. Suponiendo que los iones en la fuente parten con velocidad nula, su velocidad u al llegar al anillo B será
La fórmula de la fuerza de empuje es
La potencia eléctrica consumida (energía por unidad de tiempo) es el producto de la intensidad del haz de iones I por el potencial acelerador V.
P=I·V
Expresamos la fuerza de empuje en términos de la potencia P
para una potencia P dada del motor, es preferible utilizar iones pesados que tengan la carga del electrón q=1e y un potencial acelerador V tan bajo como sea posible.
El papel del filamento F que inyecta electrones al haz
Si no se añaden electrones al haz, es decir, se desconecta el filamento F, el cohete va perdiendo carga positiva, llegará un momento en que adquiera un potencial igual al que sirve para acelerar los iones. En estas condiciones, el motor deja de funcionar, ya que los iones no son acelerados y siguen al cohete.
Supongamos que la corriente es I, que el potencial acelerador es V, y que el cohete tiene forma esférica de radio R.
El potencial V de un conductor esférico de radio R cargado con una carga Q, es
La relación entre carga e intensidad es
Q=I·t
Dado V, I y R, calculamos el tiempo que transcurre hasta que deja de funcionar el motor iónico si se desconecta la fuente F de electrones.
Ejemplo:
Sea R=1 m, I=1 A, y V=50000 V, tenemos que t=5.5 microsegundos, es el tiempo que tarda en dejar de funcionar el cohete.
Dinámica del cohete
La segunda ley de Newton se enuncia: la masa por la aceleración del cohete es igual a la fuerza de empuje. La masa M del cohete es prácticamente constante, ya que la masa del combustible expulsado como veremos más adelante, es despreciable frente a la carga útil, por lo que la aceleración a es constante.
Actividades
El applet simula el funcionamiento básico de un cohete provisto de un motor iónico, para que pueda ser comparado con un cohete estándar de combustible sólido o líquido.
Se introduce
- La diferencia de potencial V entre la fuente de iones y el anillo acelerador, en el control titulado Diferencia de potencial.
- La intensidad I del haz de iones, en el control titulado Intensidad
- La masa mp de los iones en unidades de masa atómica (1 uma=1.67·10-27 kg), en el control titulado Masa
- La carga q, en unidades de la carga del electrón (e=1.6·10-19 C) en el control titulado Carga ión
- La masa M del cohete, en el control titulado Masa del cohete
Se pulsa el botón titulado Nuevo
Ejemplo:
- Sea la intensidad del haz I=1 A.
- El potencial acelerador V=50000 V
- El combustible empleado son protones cuya masa es mp=1 uma y cuya carga es q=1 e.
- El cohete tiene una masa de M=1 kg.
La pérdida de masa en cada segundo es
La masa del combustible expulsado es despreciable frente a la carga útil del cohete.
Si el cohete tiene una masa M=1 kg, y su aceleración es de a=0.032 m/s2, en el espacio exterior recorre 1.6 m en 10 s, partiendo del reposo.
Probar el funcionamiento del cohete en las siguientes situaciones:
Con la misma potencia P=I·V, es decir, que el producto de intensidad por diferencia de potencial sea constante, comparar los siguientes casos:
- V=5000, I=10 A
- V=50000, I=1 A
- Comprobar el efecto de la masa de los iones: ligeros mp=1 uma y iones pesados mp=50 uma;
- Comprobar el efecto de la carga q= 1e, q=3e.
Ejemplo
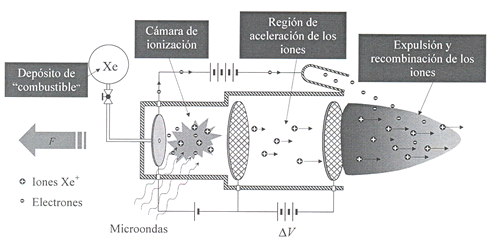
Los átomos neutros de gas Xenón entran en una primera cámara donde son ionizados mediante un haz de microondas, que arrancan un electrón a cada átomo. Los iones Xe+ son conducidos mediante un campo eléctrico débil a otra cámara, donde un intenso campo eléctrico los acelera hasta alta velocidad y los expulsa hacia el espacio exterior. La nave debe permanecer eléctricamente neutra, por lo que un circuito capta los electrones producidos en la ionización y los expulsa también al espacio donde se recombinan con los iones Xe+ formando de nuevo gas neutro. Los electrones son mucho más ligeros que los iones, por lo que su efecto de propulsión es despreciable.
El SMART-1 inició su viaje con una carga de 80 kg de gas Xenón. El motor iónico tiene un consumo de 0.10 kg/día de Xe , lo que da una autonomía superior a dos años. La diferencia de potencial entre las rejillas aceleradoras es de 1300 V. Datos
- Masa de un átomo de Xe, 130 uma, 2.180·10-25 kg
- Energía necesaria para que un átomo Xe se convierta en ión Xe+, 12.13 eV
- Carga del electrón, 1.6·10-19 C
Los iones son expulsados con una velocidad de
La fuerza de empuje es
Carga expulsada por segundo es igual al número de iones expulsados por segundo por la carga de cada ión. El número de iones expulsados por segundo es
La potencia eléctrica empleada en la aceleración de los iones es
Energía por unidad de tiempo necesaria para ionizar los átomos de Xe
El número de átomos expulsados por segundo, coincide con el número de átomos ionizados por segundo. por la energía necesaria para
La potencia total es
P=Pi+Pa=1104+10.3=1114.6 W
Referencias
Lorrain P., Corson D. Campos y Ondas Electromagnéticas. Selecciones Científicas (1972), problema 4.28, págs. 203-204
XVI Olimpiada Española de Física. Propulsión iónica (prueba teórica) Universidad de Almería (2005)

