Obstáculo en forma de disco

Estudiamos ahora, el comportamiento de un conjunto de partículas que incide sobre un obstáculo fijo en forma de disco de radio R. Supondremos el choque entre la partícula y el obstáculo es perfectamente elástico.

El parámetro de impacto b es la distancia entre la dirección de la velocidad de la partícula y el centro del disco. Como vemos en la figura, la relación entre el parámetro de impacto b y el ángulo de dispersión Φ es

${\displaystyle \Phi =\pi -2\phi =\pi -2\arcsin \left(\frac{b}{R}\right)}$

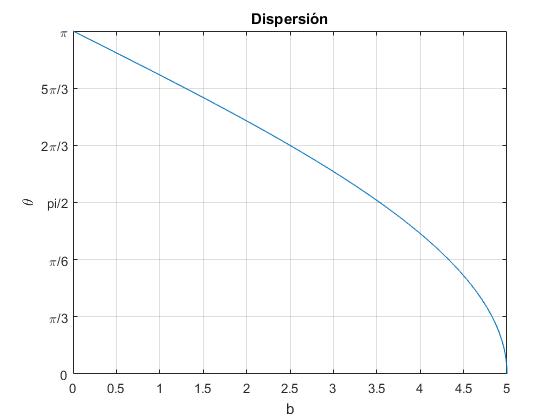
Representamos el ángulo de dispersión Φ en función del parámetro de impacto b. Cuanto mayor es el parámetro de impacto menor es el ángulo de dispersión.

R=5; %radio
f=@(x) pi-2*asin(x/R);
fplot(f,[0,5])
grid on
set(gca,'YTick',0:pi/6:pi)
set(gca,'YTickLabel',{'0','\pi/3','\pi/6','pi/2','2\pi/3', '5\pi/3','\pi'})
xlabel('b')
ylabel('\theta')
title('Dispersión')

Actividades

• El radio del disco se ha fijado en R=5

Se pulsa el botón titulado Nuevo y a continuación, ►

Observamos el movimiento de las partículas cuya velocidad es paralela al eje X, y el choque con el obstáculo en forma de disco que cambia la dirección de su velocidad formando un ángulo con la dirección incidente denominado ángulo de dispersión Φ.

Obstáculo en forma de parábola

Estudiamos ahora, el comportamiento de un conjunto de partículas que incide sobre un obstáculo fijo en forma de parábola

${\displaystyle y^2=c^{2}x}$

donde c es una constante

Supondremos el choque entre la partícula y el obstáculo es perfectamente elástico.

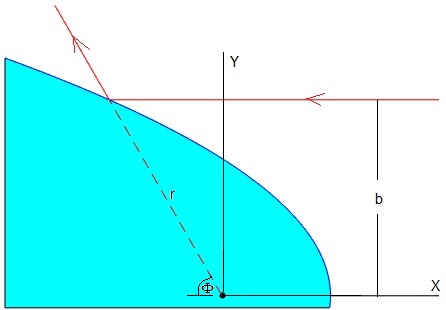
El movimiento de las partículas es paralelo al eje X. Como vemos en la figura, en la posición de impacto b=y

${\displaystyle \Phi =2\phi \tan \phi =\frac{dy}{dx}=\frac{c}{2\sqrt{x}}=\frac{c^2}{2b}}$

φ es el ángulo que forma la tangente a la curva en el punto de abscisa x, con el eje X.

La relación entre le parámetro de impacto b y el ángulo de dispersión Φ es

${\displaystyle \tan \left(\frac{\Phi }{2}\right)=\frac{c^2}{2b}}$

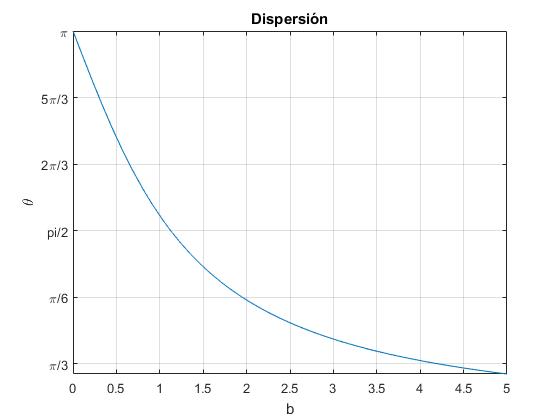
Representamos el ángulo de dispersión Φ en función del parámetro de impacto b. Cuanto mayor es el parámetro de impacto menor es el ángulo de dispersión.

c=1.5; %parámetro
f=@(x) 2*atan(c^2./(2*x));
fplot(f,[0,5])
grid on
set(gca,'YTick',0:pi/6:pi)
set(gca,'YTickLabel',{'0','\pi/3','\pi/6','pi/2','2\pi/3', '5\pi/3','\pi'})
xlabel('b')
ylabel('\theta')
title('Dispersión')

Otra forma de obtener el ángulo de dispersión

El espejo parabólico tiene la propiedad de que un rayo paralelo al eje pasa por el foco

La ecuación de una parábola en coordenadas polares es

${\displaystyle r=\frac{d}{1+\cos \theta }}$

Para dibujar parte de la figura (más abajo), se ha utilizado el siguiente código

ang=(-10:120)*pi/180;
d=2; 
r=d./(1+cos(ang));
x=[r.*cos(ang), r(end)*cos(ang(end)), r(1)*cos(ang(1))];
y=[r.*sin(ang), r(1)*sin(ang(1)), r(1)*sin(ang(1))];
hold on
fill(x,y,'c') %obstáculo
plot(r.*cos(ang),r.*sin(ang),'b')
plot(0,0,'o','markersize',4,'markeredgecolor','k','markerfacecolor','k')
line([f,2],[0,0],'color','k')
angulo=70*pi/180;
r1=2*f/(1+cos(angulo));
line([0,r1*cos(angulo)],[0,r1*sin(angulo)],'color','r','lineStyle','--')
line([r1*cos(angulo),2],[r1*sin(angulo),r1*sin(angulo)],'color','r')
line([r1*cos(angulo),r1*cos(angulo)+1],[r1*sin(angulo),
r1*sin(angulo)+1*tan(angulo)],'color','r')
hold off
axis off

El origen está en el foco y el vértice en la posición θ=0, x=d/2, y=0

La relación entre parámetro de impacto b y ángulo de dispersión Φ es ahora, más evidente

${\displaystyle b=r\sin \Phi =\frac{d}{1-\cos \Phi }\sin \Phi }$

Elevando al cuadrado, despejamos cosΦ

${\displaystyle \Phi =\arccos \left(\frac{b^2-d^2}{b^2+d^2}\right)}$

Anteriormente, hemos deducido la relación

${\displaystyle \tan \left(\frac{\Phi }{2}\right)=\frac{c^2}{2b}}$

Por otra parte,

${\displaystyle \tan \Phi =\frac{2\tan \left(\Phi /2\right)}{1-{\tan }^2\left(\Phi /2\right)}=\frac{4b{c}^2}{4b^2-c^4}}$

Finalmente,

${\displaystyle \begin{array}{l}\frac{1}{{\cos }^2\Phi }=1+{\tan }^2\Phi \\ \cos \Phi =\frac{4b^2-c^4}{4b^2+c^4}=\frac{b^2-{\left(c^2/2\right)}^2}{4b^2+{\left(c^2/2\right)}^2}\end{array}}$

Tomando d=c²/2, obtenemos la misma expresión para el ángulo de dispersión Φ en función del parámetro de impacto b

d=1.5^2/2; %la misma curva de dispersión; 
f=@(x) acos((-d^2+x.^2)./(d^2+x.^2));
fplot(f,[0,5])
grid on
set(gca,'YTick',0:pi/6:pi)
set(gca,'YTickLabel',{'0','\pi/3','\pi/6','pi/2','2\pi/3', '5\pi/3','\pi'})
xlabel('b')
ylabel('\theta')
title('Dispersión')

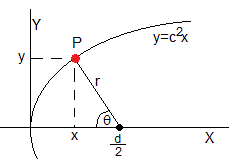
Como vemos en la figura

Las coordenadas del punto P son x=d/2-rcosθ, y=rsinθ

Por otra parte, la ecuación de la parábola en coordenadas polares es r=d/(1+cosθ)

${\displaystyle \begin{array}{l}d=r+r\cos \theta \\ d=\sqrt{{\left(d/2-x\right)}^2+y^2}+\left(d/2-x\right)\end{array}}$

Elevando al cuadrado, obtenemos

y=2dx. Que es una parábola con c²=2d

Actividades

El valor de la constante se ha fijado en c=1.5

Se pulsa el botón titulado Nuevo y a continuación, ►

Observamos el movimiento de las partículas cuya velocidad es paralela al eje X y el choque con el obstáculo en forma de parábola que cambia la dirección de su velocidad formando un ángulo con la dirección incidente denominado ángulo de dispersión Φ. Las prolongaciones (líneas a trazos de color azul) de las trayectorias después del choque con la superficie, pasan por el foco de la parábola

Referencias

Brun J. L., Pacheco A. F. Differential cross-sections with hard targets. Eur. J. Phys. 26 (2005) pp. 747-755