La dispersión en el Sistema de Referencia del c.m. y del Laboratorio

Como el problema de dos cuerpos es reducible a otro de un solo cuerpo, cabe imaginar que sería suficiente sustituir la masa m por la masa reducida μ. Sin embargo, el ángulo de dispersión que se mide en el laboratorio resulta algo más complicado de calcular.

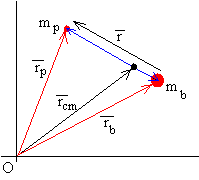
Si $\vec{r} = \vec{r_{p}} - \vec{r_{b}}$ es la posición del proyectil respecto del blanco, la posición de cada una de las partículas respecto del c.m. es

$\begin{array}{l} \vec{r_{p c m}} = \vec{r_{p}} - \vec{r_{c m}} = \frac{m_{b} \vec{r}}{m_{p} + m_{b}} \\ \vec{r_{b c m}} = \vec{r_{b}} - \vec{r_{cm}} = - \frac{m_{p} \vec{r}}{m_{p} + m_{b}} \end{array}$

Las velocidades de las partículas respecto del S.R. del c.m. están relacionadas de forma análoga.

$\begin{array}{l} \vec{v_{p c m}} = \vec{v_{p}} - \vec{v_{c m}} = \frac{m_{b} \vec{v}}{m_{p} + m_{b}} \\ \vec{v_{b c m}} = \vec{v_{b}} - \vec{v_{c m}} = - \frac{m_{p} \vec{v}}{m_{p} + m_{b}} \end{array}$

La energía cinética es la suma de la energía cinética de las partículas en el S.R. del c.m. y la energía cinética del c.m. donde suponemos concentrada toda la masa del sistema.

$\begin{array}{l} E_{k} = \frac{1}{2} m_{p} v_{p c m}^{2} + \frac{1}{2} m_{b} v_{b c m}^{2} + \frac{1}{2} (m_{p} + m_{b}) v_{c m}^{2} \\ = \frac{1}{2} \frac{m_{p} m_{b}}{m_{p} + m_{b}} v^{2} + \frac{1}{2} (m_{p} + m_{b}) v_{c m}^{2} = \frac{1}{2} μ v^{2} + \frac{1}{2} (m_{p} + m_{b}) v_{c m}^{2} \end{array}$

El momento angular, se puede expresar como la suma de dos contribuciones, el momento angular de las partículas respecto del c.m. y el momento angular del c.m.

$\begin{array}{l} \vec{L} = \vec{L_{c m}} + (m_{p} + m_{b}) \cdot \vec{r_{c m}} \times \vec{v_{c m}} \\ \vec{L_{c m}} = (\vec{r_{p c m}} \times m_{p} \vec{v_{p c m}}) + (\vec{r_{b c m}} \times m_{b} \vec{v_{b c m}}) = \frac{m_{p} m_{b}}{m_{p} + m_{b}} (\vec{r} \times \vec{v}) = μ (\vec{r} \times \vec{v}) \end{array}$

Las ecuaciones del movimiento del proyectil respecto del blanco se escriben de forma análoga a las de una partícula bajo la acción de un centro fijo de fuerzas, basta sustituir la masa m por la masa reducida μ , la energía E y el momento angular $\vec{L}$ , por sus valores análogos E_cm y $\vec{L_{c m}}$ medidos en el S.R. del c.m.

$\begin{array}{l} E_{c m} = \frac{1}{2} μ v^{2} + \frac{1}{4 π ε_{0}} \frac{Q q}{r} \\ L_{c m} = μ r^{2} \frac{d θ}{d t} \end{array}$

A partir de estas dos ecuaciones, obtenemos la ecuación de la trayectoria r=r(θ) en coordenadas polares. La trayectoria del proyectil respecto del blanco es una hipérbola

$r = \frac{d}{ε \cos (θ - θ_{0}) - 1} ε = \sqrt{1 + \frac{2 E_{c m} L_{c m}^{2}}{μ k^{2}}} d = \frac{L_{c m}^{2}}{μ k} k = \frac{q Q}{4 π ε_{0}}$

Trayectorias

En el sistema de referencia del centro de masas, las posiciones de los cuerpos de masas m_p y m_b son

$\begin{array}{l} \vec{r_{p c m}} = \frac{m_{b}}{m_{p} + m_{b}} \frac{d}{ε \cos θ - 1} \hat{r} \\ \vec{r_{b c m}} = - \frac{m_{p}}{m_{p} + m_{b}} \frac{d}{ε \cos θ - 1} \hat{r} \end{array}$

Donde θ es la posición angular, el vector unitario indica la dirección de la línea que une ambos cuerpos

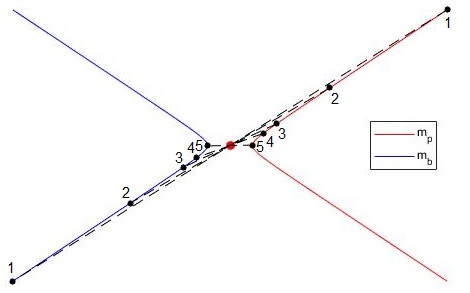
Dibujamos las trayectorias relativas al CM de dos partículas de masas m_p y m_b, de excentricidad ε, asignamos al parámetro d=1

m_p=m_b, ε=1.2

mp=1; %masas
mb=mp;
e=1.2; %excentricidad

%trayectorias en el sistema CM
th=1:acosd(1/e)-1;
radio=1./(e*cos(th*pi/180)-1);
x1=radio.*cos(th*pi/180)*mb/(mp+mb);
y1=radio.*sin(th*pi/180)*mb/(mp+mb);
x2=-radio.*cos(th*pi/180)*mp/(mp+mb);
y2=-radio.*sin(th*pi/180)*mp/(mp+mb);
hold on
plot(x1,y1,'r')
plot(x2,y2,'b')
plot(x1,-y1,'r')
plot(x2,-y2,'b')
plot(0,0,'o','markersize',6,'markeredgecolor','r','markerfacecolor','r') 

%posiciones
for pos=[1, 20, 25, 30, 32]
    line([x1(pos),x2(pos)],[y1(pos),y2(pos)],'lineStyle','--', 'color','k')
    plot(x1(pos),y1(pos),'o','markersize',4,'markeredgecolor',
'k','markerfacecolor','k')
    plot(x2(pos),y2(pos),'o','markersize',4,'markeredgecolor',
'k','markerfacecolor','k')
end
legend('m_p','m_b', 'location','best')

hold off
axis off
axis equal

m_b=2m_p, ε=1.2

Cambiamos la segunda línea de código

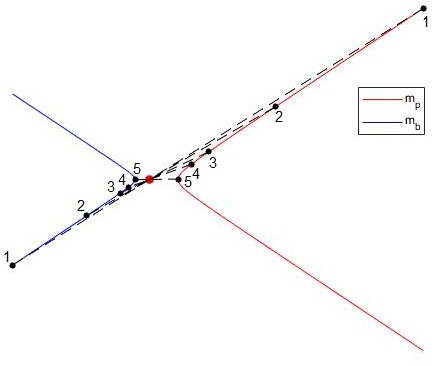
El centro de masas está en el origen y se trazan las trayectorias hiperbólicas de los dos cuerpos y se señalan sus posiciones para un ángulo dado θ. La línea que une ambas posiciones pasa por el c.m. y se cumplirá que m_pr_p=m_br_b. Como m_b es el doble que m_p, la distancia del centro de masas al primer cuerpo r_b, será la mitad que r_p

Dispersión

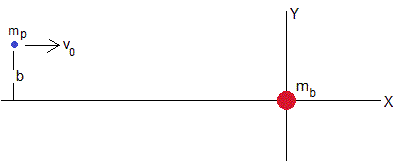
Calculemos los valores de E_cm y L_cm para una partícula proyectil con velocidad v₀ y parámetro de impacto b, que se lanza contra un blanco inicialmente en reposo.

Los valores de E y L respecto del sistema de referencia fijo en el laboratorio son

$L = m_{p} v_{0} b E = \frac{1}{2} m_{p} v_{0}^{2}$

La posición y la velocidad del centro de masas es

$y_{c m} = \frac{m_{p} b}{m_{p} + m_{b}} v_{c m} = \frac{m_{p} v_{0}}{m_{p} + m_{b}}$

La energía y el momento angular en el S.R. del c.m. son

$\begin{array}{l} E_{c m} = \frac{1}{2} μ v_{0}^{2} \\ L_{c m} = μ v_{0} b \end{array}$

En la figura, representamos r=r(θ), se señala el ángulo entre la dirección inicial y final de la velocidad v₀ que es π-2arccos(1/ε)

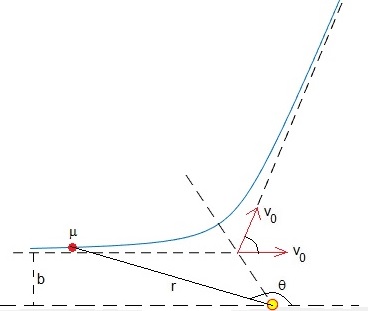
Movimiento del proyectil y del blanco en el S.R. del c.m.

Conocido r(θ) determinamos la trayectoria del proyectil y del blanco en el SR del c.m. Para ello, basta relacionar la posición relativa $\vec{r}$ (posición del proyectil respecto del blanco) con $\vec{r_{p c m}}$ (posición del proyectil respecto del c.m.) y con $\vec{r_{b c m}}$ (posición del blanco respecto del c.m.) tal como hemos hecho al principio de esta página.

$\begin{array}{l} \vec{r_{p c m}} = \vec{r_{p}} - \vec{r_{c m}} = \frac{m_{b} \vec{r}}{m_{p} + m_{b}} \\ \vec{r_{b c m}} = \vec{r_{b}} - \vec{r_{c m}} = - \frac{m_{p} \vec{r}}{m_{p} + m_{b}} \end{array}$

El ángulo de dispersión, es decir, el ángulo que forma la dirección del proyectil antes y después del proceso de dispersión, se calcula con la fórmula ya deducida en la que se ha sustituido la masa m por la masa reducida μ.

$\tan \frac{Φ}{2} = \frac{k}{2 E_{c m} b}$

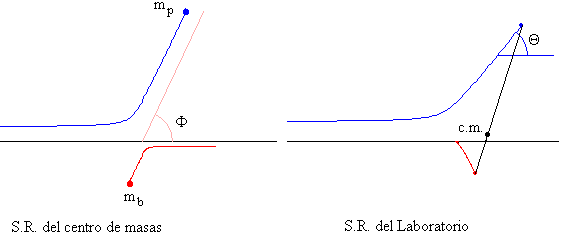
En la figura de la izquierda, vemos como aparecería el proceso de dispersión para un observador situado en el sistema de referencia del c.m, (la trayectoria del proyectil se muestra en color azul, y la del blanco en color rojo). Las partículas se mueven con momentos lineales iguales y opuestos. Se señala el ángulo de dispersión, es decir, el ángulo que forma la dirección inicial y la final del proyectil.

Las partículas antes y después de la dispersión (cuando se encuentran suficientemente alejadas para considerar que la interacción es despreciable) tienen el mismo módulo de la velocidad,

$v_{p c m} = \frac{m_{b}}{m_{p} + m_{b}} v_{0}$

su dirección ha cambiado de dirección un ángulo Φ, que es el denominado ángulo de dispersión.

Movimiento del proyectil y del blanco en el S.R. del Laboratorio

En la parte derecha de la figura anterior, vemos la trayectoria seguida por el proyectil (en azul) y por el blanco (en rojo) en el S.R. del Laboratorio, también se señala la posición del c.m mediante un punto de color negro.

Como estamos estudiando un sistema aislado de dos partículas interactuantes, el centro de masas se mueve con velocidad constante.

$\begin{array}{l} x_{c m} = x_{0 c m} + \frac{m_{p}}{m_{p} + m_{b}} v_{0} \cdot t \\ y_{c m} = \frac{m_{p} b}{m_{p} + m_{b}} \end{array}$

donde x_0cm, es la posición inicial del c.m.

Conocidas la posición del proyectil $\vec{r_{p c m}}$ y del blanco $\vec{r_{b c m}}$ respecto del c.m. y la posición $\vec{r_{c m}}$ del centro de masas, determinamos la posición del proyectil $\vec{r_{p}}$ y del blanco $\vec{r_{b}}$ en el S. R. del Laboratorio.

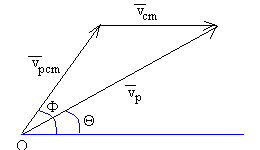
$\begin{array}{l} \vec{r_{p}} = \vec{r_{p c m}} + \vec{r_{c m}} \\ \vec{r_{b}} = \vec{r_{b c m}} + \vec{r_{c m}} \end{array}$

Velocidades

$\begin{array}{l} \vec{v_{p}} = \vec{v_{p c m}} + \vec{v_{c m}} \\ \tan Θ = \frac{v_{p c m} \sin Φ}{v_{p c m} \cos Φ + v_{c m}} \end{array}$

En la figura anterior y en ésta, vemos la relación entre el ángulo de dispersión Φ medido en el SR del c.m. con el ángulo de dispersión Θ medido en el S.R. del Laboratorio, para ello, basta establecer la relación entre las velocidades finales del proyectil $\vec{v_{p c m}}$ en el SR del c.m., la velocidad final del proyectil $\vec{v_{p}}$ en el S.R. del Laboratorio y la velocidad constante del centro de masa $\vec{v_{c m}}$ .

Como ya hemos mencionado, el proyectil antes y después de la dispersión tiene el mismo módulo de la velocidad en el S.R. del c.m, las direcciones de la velocidad inicial y final han cambiado solamente de dirección un ángulo Φ.

Sustituyendo en la última fórmula la velocidad del centro de masa v_cm y la velocidad final v_pcm del proyectil medida en el S.R. del c.m, obtenemos la relación entre los ángulos de dispersión medidos en el S.R. del Laboratorio y en el S.R. del c.m.

$\tan Θ = \frac{\sin Φ}{\cos Φ + \frac{m_{p}}{m_{b}}}$

Como el proyectil y el blanco forman un sistema aislado, la energía cinética total antes y después del proceso de dispersión se conserva.

El blanco se encuentra inicialmente en reposo y como resultado de la dispersión, retrocede. Para que se conserve la energía, el proyectil habrá de experimentar una disminución de su velocidad y energía cinética. Por tanto, como consecuencia del proceso de dispersión hay una transferencia de energía del proyectil al blanco.

En la figura anterior, tenemos que $\vec{v_{p c m}} = \vec{v_{p}} - \vec{v_{c m}}$ . Los módulos de estos vectores están relacionados

$\begin{array}{l} v_{p c m}^{2} = v_{p}^{2} + v_{c m}^{2} - 2 v_{p} v_{c m} \cos Θ \\ v_{p c m} = \frac{m_{b} v_{0}}{m_{p} + m_{b}} v_{c m} = \frac{m_{p} v_{0}}{m_{p} + m_{b}} \end{array}$

La velocidad final del proyectil es la raíz positiva de ecuación de segundo grado en v_p/v₀.

${(\frac{v_{p}}{v_{0}})}^{2} - \frac{2 μ}{m_{b}} (\frac{v_{p}}{v_{0}}) \cos Θ - \frac{m_{b} - m_{p}}{m_{b} + m_{p}} = 0$

En el caso especial de que m_p=m_b tenemos que v_p/v₀=cos Θ.

Así para un ángulo de dispersión de Θ=90º en el S.R. del Laboratorio lo que corresponde una dispersión de Φ=180º en el S.R. del c.m., se produce una transferencia máxima de energía y la partícula que retrocede (el blanco) adquiere toda la energía cinética inicial.

Esta transferencia de energía cinética mediante dispersión constituye el principio de los moderadores en las pilas de neutrones lentos. Los neutrones rápidos producidos en la fisión experimentan sucesivos procesos de dispersión hasta que su energía cinética se reduce. Los mejores moderadores son los elementos ligeros, idealmente el hidrógeno, aunque en la práctica se utilizan el deuterio (masa 2) y el carbono (masa 12).

Actividades

Se introduce

La energía cinética E de la partícula incidente, en el control titulado Energía.
El parámetro de impacto b, en el control titulado P. impacto
Se ha fijado la masa de la partícula incidente m_p=1
La masa del blanco m_b, en el control titulado Masa blanco.

Se elige entre dos posible opciones:

El observador situado en el centro de masa (S.R. del c.m.)
El observador fijo en el laboratorio (S.R. del Laboratorio)

Finalmente, se pulsa en el botón titulado Nuevo.

El programa, traza las trayectorias del proyectil y del blanco y calcula los ángulos de dispersión. El programa interactivo compara la velocidad inicial de la partícula con la velocidad final. En ambos casos se supone que las partículas están suficientemente alejadas para considerar que su interacción mutua es despreciable.

Observamos que en el S.R. de c.m. el proceso de dispersión no cambia el módulo de la velocidad, aunque si cambia su dirección.

En el S.R. del laboratorio, la velocidad final del proyectil es menor que la inicial y el blanco incrementa su velocidad debido a la interacción. Por tanto, en este S.R. hay un cambio tanto en el módulo como en la dirección de la velocidad de la partícula incidente.

Ejemplo 1:

Introduzcamos los siguientes datos

Energía cinética del proyectil E=0.75
Parámetro de impacto b=0.5
Masa del proyectil m_p=1
Masa del blanco m_b=1

Establecemos un Sistema de Unidades en el que k=1

La velocidad del proyectil en el S.R. del Laboratorio es

$E = \frac{1}{2} m_{p} v_{0}^{2} v_{0} = 1.22$

La masa reducida μ es

$\frac{1}{μ} = \frac{1}{m_{p}} + \frac{1}{m_{b}} μ = 0.5$

La energía cinética del proyectil en el S.R. del c.m. vale

$E_{c m} = \frac{1}{2} μ v_{0}^{2} E_{c m} = 0.375$

El ángulo de dispersión Φ en el S.R. del c.m. vale

$\tan \frac{Φ}{2} = \frac{k}{2 E_{c m} b} Φ = 138.9 º$

El ángulo de dispersión medido en el Laboratorio vale

$\tan Θ = \frac{\sin Φ}{\cos Φ + \frac{m_{p}}{m_{b}}} Θ = 69.4 º$

Calculamos la velocidad del proyectil después de la dispersión, resolviendo la ecuación de segundo grado

v_p=0.43 m/s.

Ejemplo 2:

Introduzcamos los siguientes datos

Energía cinética del proyectil E=0.75
Parámetro de impacto b=0.5
Masa del proyectil m_p=1
Masa del blanco m_b=50

La masa del blanco es mucho mayor que la masa del proyectil. Los resultados son

La velocidad del proyectil en el S.R. del Laboratorio es v₀=1.22

La masa reducida es μ =0.98

La energía cinética del proyectil en el S.R. del c.m. vale E_cm=0.735

El ángulo de dispersión Φ en el S.R. del c.m. vale Φ =107.3º

El ángulo de dispersión medido en el Laboratorio vale Θ=106.2º

Calculamos la velocidad del proyectil después de la dispersión, resolviendo la ecuación de segundo grado

v_p=1.19 m/s.

Las trayectorias que sigue el proyectil en el S.R. de c.m. y en el S.R. de laboratorio son parecidas. El ángulo de dispersión es aproximadamente el mismo. Estamos aproximadamente, en el caso de dispersión de una partícula por un centro fijo de fuerzas.

Energía: P. impacto:
Masa blanco: