Eje horizontal, partícula con carga negativa

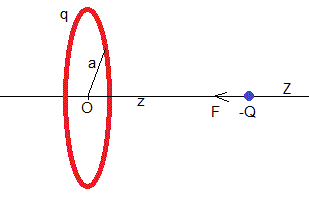
Sea un anillo de radio a cargado con carga positiva +q. Situamos una partícula de masa m y carga -Q en la posición z₀ y la soltamos. Vamos a determinar el movimiento de la carga

La fuerza sobre la carga -Q es el producto del campo E_z por dicha carga. La segunda ley de Newton se escribe

${\displaystyle m\frac{d^{2}z}{d{t}^2}=-Q\left(\frac{1}{4\pi {\epsilon }_0}\frac{qz}{{\left(a^2+z^2\right)}^{3/2}}\right)}$

La ecuación diferencial del movimiento es

${\displaystyle \frac{d^{2}z}{d{t}^2}+\frac{1}{4\pi {\epsilon }_0}\frac{Qq}{m{a}^3}\left(\frac{z}{{\left(1+{\left(\frac{z}{a}\right)}^2\right)}^{3/2}}\right)=0}$

Cuando la posición inicial z₀ de la carga -Q es próxima al origen y el radio a del anillo es grande, se cumple que z<<a o z/a<<1, la ecuación se puede aproximar a

${\displaystyle \frac{d^{2}z}{d{t}^2}+\frac{1}{4\pi {\epsilon }_0}\frac{Qq}{m{a}^3}z=0}$

Se trata de la ecuación de un Movimiento Armónico Simple de frecuencia angular

${\displaystyle \omega =\sqrt{\frac{1}{4\pi {\epsilon }_0}\frac{Qq}{m{a}^3}}}$

La posición de la carga -Q, en función del tiempo t es z=z₀cos(ωt), sabiendo que parte del reposo desde la pisción inicial z₀

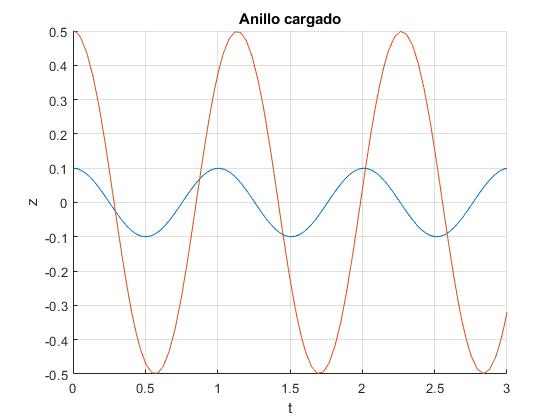
En el caso general, resolvemos la ecuación diferencial empleando el procedimiento numérico ode45 de MATLAB, con las siguientes condiciones iniciales: en el instante t=0, z=z₀ y (dz/dt)₀=0 (parte del reposo). Representamos la posición z en función del tiempo t para dos valores iniciales de z₀, 0.5·a y 0.1·a. Vemos que el primero describe una oscilación cuyo periodo es mayor que 2π/ω. Para realizar este cálculo, se ha tomado un valor de ω=2π o periodo P=2π/ω=1 s, el radio del anillo a=1

w=2*pi; %frecuencia nagular
a=1; %radio del anillo
hold on
for z0=[0.1,0.5]*a
    fg=@(t,x) [x(2);-w^2*x(1)/(1+(x(1)/a)^2)^(3/2)];
    [t,x]=ode45(fg,[0,3*2*pi/w],[z0,0]);
    plot(t,x(:,1))
end
hold off
grid on
xlabel('t')
ylabel('z');
title('Anillo cargado')

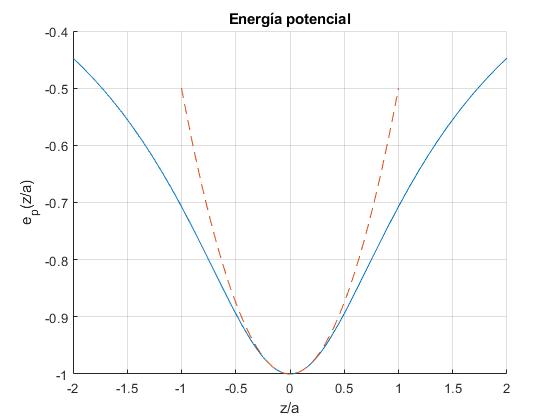
La energía potencial es

${\displaystyle E_p(z)=-\frac{1}{4\pi {\epsilon }_0}\frac{qQ}{\sqrt{a^2+z^2}}=-\frac{qQ}{4\pi {\epsilon }_{0}a}\frac{1}{\sqrt{1+{\left(\frac{z}{a}\right)}^2}}}$

Representamos la energía potencial E_p(z/a) y su aproximación para z/a<<1 (línea a trazos)

>> syms x;
>> taylor(-1/sqrt(1+x^2),x)
 ans =- (3*x^4)/8 + x^2/2 - 1

${\displaystyle E_p(z)\approx -\frac{qQ}{4\pi {\epsilon }_{0}a}\left(-1+\frac{1}{2}{\left(\frac{z}{a}\right)}^2+\mathrm{...}\right)}$

f=@(z) -1./sqrt(1+z.^2);
hold on
fplot(f,[-2,2])
fplot(@(x) -1+x.^2/2,[-1,1],'lineStyle','--')
hold off
xlabel('z/a')
ylabel('e_p(z/a)')
grid on
title('Energía potencial')

Sabiendo que la energía potencial de un oscilador armónico es

${\displaystyle E_p(x)=\frac{1}{2}m{\omega }^2{x}^2,x=\frac{z}{a}}$

obtenemos la frecuencia angular ω del oscilador

Eje vertical, partícula con carga positiva

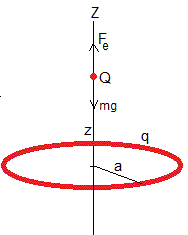
Una partícula de masa m y carga Q se puede mover a la largo del eje vertical Z de un anillo cargado con carga q del mismo signo y de radio a. Las fuerzas sobre la partícula cargada son:

• El peso, mg

• La fuerza de resulsión, F_e

${\displaystyle F_e=QE=\frac{qQ}{4\pi {\epsilon }_0}\frac{z}{{\left(a^2+z^2\right)}^{3/2}}}$

La fuerza de repulsión eléctrica alcanza su valor máximo para z_m tal que, la derivada es nula

${\displaystyle \begin{array}{l}\frac{d{F}_e}{dz}=\frac{qQ}{4\pi {\epsilon }_0}\frac{{\left(a^2+z^2\right)}^{3/2}-\frac{3}{2}2z^2{\left(a^2+z^2\right)}^{1/2}}{{\left(a^2+z^2\right)}^3}=0\\ a^2-2z^2=\mathrm{0,}{z}_m=\pm \frac{a}{\sqrt{2}}\end{array}}$

Para esta posición z_m la fuerza de repulsión F_evale

${\displaystyle F_e=\frac{qQ}{4\pi {\epsilon }_0}\frac{\frac{a}{\sqrt{2}}}{{\left(a^2+{\frac{a}{2}}^2\right)}^{3/2}}=\frac{2}{\sqrt{27}}\frac{qQ}{4\pi {\epsilon }_0{a}^2}}$

Para que se equilibren, la fuerza de repulsión y el peso, la masa de la partícula cargada deberá ser inferior a la máxima posible M tal que

${\displaystyle Mg=\frac{2}{\sqrt{27}}\frac{qQ}{4\pi {\epsilon }_0{a}^2}}$

La energía potencial de una partícula de masa m<M y carga Q es

${\displaystyle E_p(z)=\frac{qQ}{4\pi {\epsilon }_0}\frac{1}{\sqrt{a^2+z^2}}+mgz}$

Dividiendo entre Mga

${\displaystyle e_p(z)=\frac{E_p(z)}{Mga}=\frac{\sqrt{27}}{2}\frac{1}{\sqrt{1+{\left(\frac{z}{a}\right)}^2}}+k\frac{z}{a},k=\frac{m}{M}}$

Representamos e_p(z/a) en función de x=z/a para k=0.3

k=0.3;
f=@(z) (sqrt(27)/2)./sqrt(1+z.^2)+k*z;
fplot(f,[-2,5])
raiz=raices_3([1,3,3*(1-9/(4*k^2)),1]);
r1=sqrt(raiz(2));
line([r1,r1],[0,f(r1)],'lineStyle','--')
r2=sqrt(raiz(3));
line([r2,r2],[0,f(r2)],'lineStyle','--')
xlabel('z/a')
ylabel('e_p(z/a)')
grid on
title('Energía potencial')

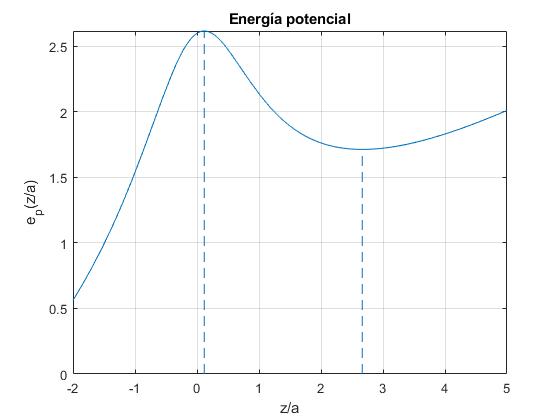
Vemos que para k<1 tiene un máximo y un mínimo.

${\displaystyle \begin{array}{l}{e}_p(x)=\frac{\sqrt{27}}{2}\frac{1}{\sqrt{1+x^2}}+kx\\ \frac{d{e}_p(x)}{dx}=-\frac{\sqrt{27}}{2}\frac{x}{{\left(1+x^2\right)}^{3/2}}+k=0\\ \frac{x^2}{{\left(1+x^2\right)}^3}=\frac{4}{27}{k}^2\\ {\left(x^2\right)}^3+3{\left(x^2\right)}^2+3\left(1-\frac{9}{4k^2}\right)\left(x^2\right)+1=0\end{array}}$

Obtenemos las raíces de la ecuación cúbica en x² mediante la función raices_3, alternativamente, mediante roots de MATLAB

La ecuación cúbica tiene tres raíces reales, una de las cuales es negativa, la raíz cuadrada de las otras dos, señalan las posiciones de máximo y del mínimo de energía potencial tal como se aprecia en la figura

Como en el apartado anterior, la partícula puede oscilar alrededor de la posición de equilibrio estable

Referencias

Physics Challenge for Teachers and Students. A ring on a string. The Physics Teacher. Vol. 54, May 2016. pp. 188