Consideremos el siguiente circuito formado por dos condensadores de capacidades C₁ y C₂, una resistencia R y una autoinducción L.

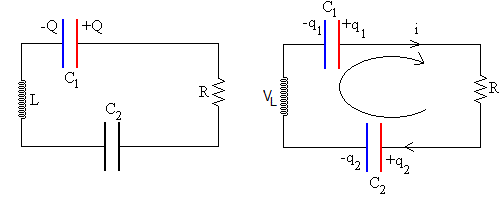
El condensador de capacidad C₁ está cargado con una carga Q y el condensador de capacidad C₂ está inicialmente descargado. En el instante t=0, se cierra el circuito. El condensador de capacidad C₁ se descarga y carga al condensador de capacidad C₂.

En un instante dado t, tendremos que

• El condensador C₁ tiene una carga q₁
• El condensador C₂ tiene una carga q₂
• Por la resistencia R circula una corriente de intensidad i.
• Por la autoinducción L circula una corriente de intensidad i.

La ecuación del circuito es

${\displaystyle \begin{array}{l}{V}_L-\frac{q_2}{C_2}+\frac{q_1}{C_1}=iR\\ \left(-L\frac{di}{dt}\right)-\frac{q_2}{C_2}+\frac{q_1}{C_1}=iR,i=\frac{d{q}_2}{dt},i=-\frac{d{q}_1}{dt}\\ q_1+q_2=Q\end{array}}$

La corriente i extrae carga de la placa positiva del condensador C₁, por lo que i=-dq₁/dt y añade carga a la placa positiva del condensador C₂, por lo que i=dq₂/dt. La conservación de la carga implica q₁+q₂=Q

La ecuación del circuito se escribe en términos de q₂

${\displaystyle \frac{d^2{q}_2}{d{t}^2}+\frac{R}{L}\frac{d{q}_2}{dt}+\left(\frac{1}{C_1}+\frac{1}{C_2}\right)\frac{q_2}{L}=\frac{Q}{L{C}_1}}$

o bien,

${\displaystyle \frac{d^2{q}_2}{d{t}^2}+2\gamma \frac{d{q}_2}{dt}+{\omega }_0^2{q}_2=\frac{Q}{L{C}_1}{\omega }_0^2=\frac{1}{L}\frac{C_1+C_2}{C_1{C}_2}\gamma =\frac{R}{2L}}$

La solución de esta ecuación diferencial es de la forma

${\displaystyle q_2=y_1+\exp (-\gamma t)(A·\text{sin}\omega t+B·\cos \omega t){\omega }^2={\omega }_0^2-{\gamma }^2}$

La constante y₁ es la solución particular. El segundo término, es la solución de la ecuación diferencial homogénea que ya encontramos en el estudio de las oscilaciones amortiguadas.

Introduciendo la solución particular y₁ en la ecuación diferencial tenemos que y₁=QC₂/(C₁+C₂)

Las condiciones iniciales q₂=0, y dq₂/dt=0 determinan los valores de A y B.

${\displaystyle \begin{array}{l}{q}_2=\frac{Q{C}_2}{C_1+C_2}\left(1-\exp (-\gamma t)\left(\frac{\gamma }{\omega }\text{sin}\omega t+\cos \omega t\right)\right)\\ i=\frac{d{q}_2}{dt}=\frac{Q}{L{C}_1}\exp (-\gamma t)\frac{\text{sin}\omega t}{\omega }\end{array}}$

Comprobamos que en el instante t=0, q₂=0 e i=0. Después de un tiempo muy grande, t→∞, i→0 y

${\displaystyle q_2\to \frac{Q{C}_2}{C_1+C_2}}$

Deducción alternativa

Derivamos la ecuación del circuito respecto del tiempo

${\displaystyle -\frac{1}{C_1}\frac{d{q}_1}{dt}+R\frac{di}{dt}+\frac{1}{C_2}\frac{d{q}_2}{dt}+L\frac{d^{2}i}{d{t}^2}=0}$

Quedando la ecuación diferencial de las oscilaciones amortiguadas

${\displaystyle \frac{d^{2}i}{d{t}^2}+2\gamma \frac{di}{dt}+{\omega }_0^{2}i=0\gamma =\frac{R}{2L}{\omega }_0^2=\frac{1}{L}\frac{C_1+C_2}{C_1{C}_2}}$

Para integrar la ecuación diferencial necesitamos conocer la intensidad i en el instante t=0, y el valor de la derivada primera di/dt de la intensidad en dicho instante.

Las condiciones iniciales son por tanto, en el instante t=0, la intensidad i=0. El condensador de capacidad C₂ se encuentra descargado q₂=0, el condensador de capacidad C₁ tiene una carga inicial q₁=Q. La ecuación del circuito se escribe para t=0

${\displaystyle -\frac{Q}{C_1}+L\frac{di}{dt}=0}$

Soluciones de la ecuación diferencial

La solución de la ecuación diferencial es la siguiente:

Oscilaciones amortiguadas(γ<ω₀)

${\displaystyle \begin{array}{l}i=A\exp (-\gamma t)·\text{sin}(\omega t+\phi ){\omega }^2={\omega }_0^2-{\gamma }^2\\ \frac{di}{dt}=A\exp (-\gamma t)\left(-\gamma ·\text{sin}(\omega t+\phi )+\omega ·\cos (\omega t+\phi )\right)\end{array}}$

Las condiciones iniciales determinan la amplitud A y la fase inicial φ.

${\displaystyle \begin{array}{l}0=A\text{sin}\phi \\ \frac{Q}{L{C}_1}=A(-\gamma \text{sin}\phi +\omega \cos \phi )\end{array}}$

La ecuación de la oscilación amortiguada es

${\displaystyle i=\frac{Q}{L{C}_1}\exp (-\gamma t)\frac{\text{sin}(\omega t)}{\omega }}$  

Oscilación crítica (γ=ω₀)

La solución de la ecuación diferencial es

${\displaystyle \begin{array}{l}i=(At+B)·\exp (-\gamma t)\\ \frac{di}{dt}=A\exp (-\gamma t)-\gamma (At+B)·\exp (-\gamma t)\end{array}}$

Las condiciones iniciales determinan las constantes A y B

${\displaystyle \begin{array}{l}0=B\\ \frac{Q}{L{C}_1}=A-\gamma B\end{array}}$

La variación de la intensidad i en función del tiempo t es

${\displaystyle i=\frac{Q}{L{C}_1}\exp (-\gamma t)·t}$

Oscilación sobreamortiguada (γ>ω₀)

La solución de la ecuación diferencial es

$$\begin{gathered} {\displaystyle \begin{array}{l}i=\left(A\exp (-\beta t)+B·\exp (\beta t)\right)\exp (-\gamma t)\\ \frac{di}{dt}=\beta \left(-A\exp (-\beta t)+B·\exp (\beta t)\right)\exp (-\gamma t)-\gamma \left(A\exp (-\beta t)+ \\ B·\exp (\beta t)\right)\exp (-\gamma t)\end{array}} \end{gathered}$$

Las condiciones iniciales determinan las constantes A y B

${\displaystyle \begin{array}{l}0=A+B\\ \frac{Q}{L{C}_1}=\beta (-A+B)-\gamma (A+B)\end{array}}$

La variación de la intensidad i en función del tiempo t es

${\displaystyle i=\frac{Q}{L{C}_1}\exp (-\gamma t)\frac{\text{sinh}(\beta t)}{\beta }}$

Carga final de los condensadores

Calculamos las cargas de cada condensador en función del tiempo con las siguientes condiciones iniciales: en el instante t=0, la carga del condensador C₁ es q₁=Q y la carga del condensador C₂ es q₂=0.

${\displaystyle \begin{array}{l}i=\frac{d{q}_2}{dt}{q}_2={\displaystyle \underset{0}{\overset{t}{\int }}i·dt}\\ i=-\frac{d{q}_1}{dt}{q}_1=Q-q_2\end{array}}$

Después de un tiempo teóricamente infinito, se establece una situación de equilibrio. Para obtener la carga final de los condensadores no es necesario proceder a la integración en cada uno de los tres casos, ya que después de un tiempo teóricamente infinito la intensidad i tiende cero y la derivada di/dt tiende también a cero. La ecuación del circuito queda

${\displaystyle -\frac{q_1}{C_1}+\frac{q_2}{C_2}=0}$

Por la conservación de la carga

${\displaystyle \begin{array}{l}{q}_1+q_2=Q\\ q_1=\frac{Q{C}_1}{C_1+C_2}{q}_2=\frac{Q{C}_2}{C_1+C_2}\end{array}}$

Estudio energético

La energía inicial almacenada en el condensador de capacidad C₁ es

${\displaystyle U_i=\frac{1}{2}\frac{Q^2}{C_1}}$

La energía almacenada en los condensadores después de un tiempo teóricamente infinito es

${\displaystyle U_f=\frac{1}{2}\frac{q_1^2}{C_1}+\frac{1}{2}\frac{q_2^2}{C_1}=\frac{1}{2}\frac{Q^2}{C_1+C_2}}$

La diferencia de energías U_f-U_i es la que se disipa en la resistencia R hasta que se establece la situación de equilibrio es

${\displaystyle \Delta U=U_f-U_i=-\frac{1}{2}\frac{Q^2}{C_1}\frac{C_2}{C_1+C_2}}$

El lector puede ejercitarse en el cálculo de integrales para demostrar que la energía disipada en la resistencia en los tres casos es

${\displaystyle U_R={\displaystyle \underset{0}{\overset{\infty }{\int }}{i}^{2}R·dt}=\frac{1}{2}\frac{Q^2}{C_1}\frac{C_2}{C_1+C_2}}$

• Oscilaciones amortiguadas

${\displaystyle U_R=\frac{Q^2}{L^2{C}_1^2}\frac{R}{{\omega }^2}{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-2\gamma t){\text{sin}}^{\text{2}}(\omega t)dt}}$

Se integra por partes. Para llegar a la expresión final se tiene en cuenta que ${\omega }^2={\omega }_0^2-{\gamma }^2$

• Oscilaciones sobreamortiguadas

${\displaystyle U_R=\frac{Q^2}{L^2{C}_1^2}\frac{R}{{\beta }^2}{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-2\gamma t){\text{sinh}}^{\text{2}}(\beta t)dt}}$

Se eleva sinh(βt)=(exp(βt)-exp(-βt))/2 al cuadrado y se multiplica por exp(-2γt), la integral es inmediata. Se ha de tener en cuenta que ${\beta }^2={\gamma }^2-{\omega }_0^2$ para llegar a la expresión final.

• Oscilaciones críticas

${\displaystyle U_R=\frac{Q^2}{L^2{C}_1^2}R{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-2\gamma t)t^{2}dt}}$

Se hace el cambio de variable x=2γt, la integral resultante es la denominada función gamma cuyo resultado se encuentra en las tablas de integrales.

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-x}{x}^{2}dx}=\Gamma (3)=2!=2}$

Para llegar al resultado final se ha de tener en cuenta que γ=ω₀

Comportamiento de un circuito real

El comportamiento de la intensidad por tanto depende de los valores de R, L y C.

Supongamos un hipotético circuito de 5 cm de radio, cuyos elementos están conectados mediante cables de cobre de 0.5 mm de radio.

La resistencia de los cables es

${\displaystyle R=\rho \frac{l}{A}=2·{10}^{-8}\frac{2\pi 0.05}{\pi {(0.0005)}^2}=0.008\Omega }$

La autoinducción se calcula mediante la siguiente fórmula

${\displaystyle L={\mu }_0\frac{D}{2}\left(\ln \frac{8D}{d}-\frac{7}{4}\right)=4\pi ·{10}^{-7}\frac{2·0.05}{2}\left(\ln \frac{8·2·0.05}{0.0005}-\frac{7}{4}\right)=3.5·{10}^{-7}\text{H}}$

D es diámetro del circuito y d es el diámetro del cable.

Si los dos condensadores son iguales y su capacidad es del orden C₁=C₂=100μF, Tendremos que la frecuencia angular propia o natural es

${\displaystyle {\omega }_0=\frac{2}{CL}=\frac{2}{100·{10}^{-6}·3.5·{10}^{-7}}=2.4·{10}^5\text{rad/s}}$

El factor de amortiguamiento es

${\displaystyle \gamma =\frac{R}{2L}=\frac{0.008}{2·3.5·{10}^{-7}}=1.1·{10}^4{\text{s}}^{\text{-1}}}$

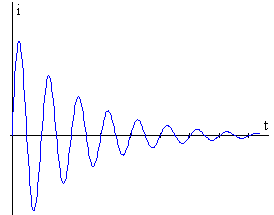
Tenemos claramente que γ/ω₀<<1. Estamos en una situación de oscilaciones amortiguadas, tal como fue nuestra suposición en base a la analogía de los vasos comunicantes.

Para dos condensadores iguales C₁=C₂=C, teniendo en cuenta que, γ<<ω₀ y por tanto, la frecuencia de la oscilación amortiguada es igual a frecuencia propia ω≈ω₀

${\displaystyle i=\frac{Q{\omega }_0}{2}\exp (-\frac{R}{2L}t)\text{sin}({\omega }_{0}t){\omega }_{\text{0}}^{\text{2}}=\frac{1}{LC}}$

Para obtener esta imagen, en la página de las oscilaciones amortiguadas, se introduce en los controles:

• Cte. de amortiguamiento, 7.0
• Posición, 0.0
• Velocidad, 500

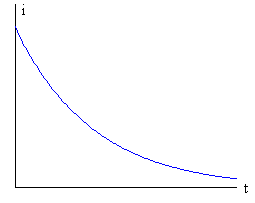
Esta solución, se puede comparar con la que se obtiene sin tener en cuenta la autoinducción del circuito

${\displaystyle i=\frac{Q}{RC}\exp \left(-\frac{t}{RC}\right)}$

que afirma que la intensidad i disminuye exponencialmente con el tiempo.

Actividades

Se introduce

• La capacidad C₁ del primer condensador en μF, inicialmente cargado, en el control titulado Capacidad 1.

• La capacidad C₂ del segundo condensador en μF, inicialmente descargado, en el control titulado Capacidad 2.

• La resistencia R, en mΩ, en el control titulado Resistencia

• La autoinducción L de la bobina, en μH, en el control titulado Autoinducción

Se pulsa el botón titulado Nuevo.

Se observa como la carga fluye de un condensador al otro, de forma análoga a como la carga fluye entre los vasos comunicantes. El flujo de cargas (la intensidad de la corriente) está representado por el movimiento de puntos de color rojo.

Si la resistencia R no es nula, la carga en cada uno de los condensadores tiende hacia un valor límite.

En la gráfica se representa, en el eje vertical la carga q₁/Q y q₂/Q y en el eje horizontal el tiempo t, medido en μs.

Ejemplo:

Se introduce

• Capacidades, C₁=3·10^-6 F, C₂=2·10^-6 F
• Resistencia, R=50·10^-3 Ω
• Autoinducción, L=2·10^-6 H

Calculamos

• La constante de amortiguamiento, γ=12500 s^-1
• La frecuencia angular natural, ω₀=645497 rad/s
• La frecuencia de la oscilación amortiguada, ω=645377 rad/s

Ambas frecuencias son prácticamente iguales

En el instante t=100·10^-6 s calculamos la carga

${\displaystyle q_2=\frac{Q{C}_2}{C_1+C_2}\left(1-\exp (-\gamma t)\left(\frac{\gamma }{\omega }\text{sin}\omega t+\cos \omega t\right)\right)}$

• en el condensador de capacidad C₂, obtenemos q₂/Q=0.41
• en el condensador de capacidad C₁, q₁/Q=1-q₂/Q=0.59

Siendo Q, la carga inicial en el instante t=0.

Después de un tiempo muy grande las cargas en cada uno de los condensadores tiende hacia

• q₂/Q=0.4
• q₁/Q=0.6

Referencias

Powell R. A.Two-capacitor problem: A more realistic view. Am. J. Phys. 47 (5) May 1979, pp. 460-462