Elementos de un circuito de corriente alterna

Una fem alterna se produce mediante la rotación de una bobina con velocidad angular constante dentro de un campo magnético uniforme producido entre los polos de un imán.

v=V ₀sin(ωt)

Para analizar los circuitos de corriente alterna, se emplean dos procedimientos, uno geométrico mediante vectores rotatorios y otro, que utiliza los números complejos.

Un ejemplo del primer procedimiento, es la interpretación geométrica del Movimiento Armónico Simple como proyección sobre el eje X de un vector rotatorio de longitud igual a la amplitud y que gira con una velocidad angular igual a la frecuencia angular.

Mediante las representaciones vectoriales, la longitud del vector representa la amplitud y su proyección sobre el eje vertical representa el valor instantáneo de dicha cantidad. Los vectores se hacen girar en sentido contrario al las agujas del reloj.

Elementos de un circuito de corriente alterna

Los elementos que se conectan a una fem alterna son: la resistencia, capacidad y autoinducción

Resistencia

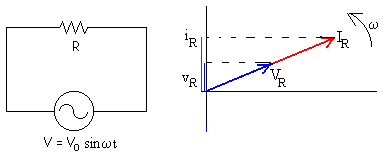
La ecuación de este circuito es (intensidad por resistencia igual a la fem)

iR=V₀sin(ωt)

$i_{R} = \frac{V_{0}}{R} \sin (ω t)$

La diferencia de potencial en los extremos de la resistencia es

v_R= V₀sin(ω t)

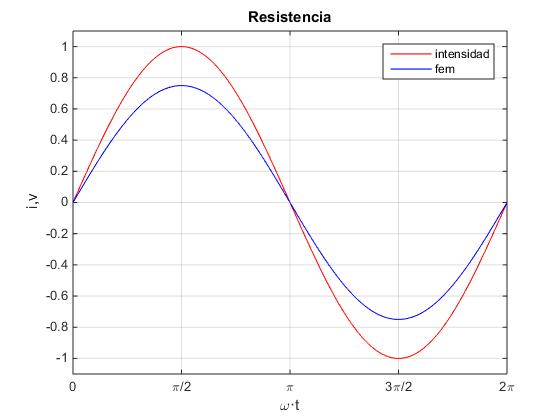
En una resistencia, la intensidad i_R y la diferencia de potencial v_R están en fase. La relación entre sus amplitudes es

$I_{R} = \frac{V_{R}}{R}$

con V_R=V₀, la amplitud de la fem alterna

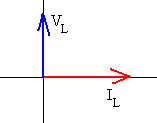
Como vemos en la representación vectorial de la figura, al cabo de un cierto tiempo t, los vectores rotatorios que representan a la intensidad en la resistencia y a la diferencia de potencial entre sus extremos, ha girado un ángulo ωt. Sus proyecciones sobre el eje vertical marcados por los segmentos de color azul y rojo son respectivamente, los valores en el instante t de la intensidad que circula por la resistencia y de la diferencia de potencial entre sus extremos.

Como V_R=R·I_R, definimos la impedancia Z_R de la resistencia

$Z_{R} = \frac{V_{R}}{I_{R}} = R$

Condensador

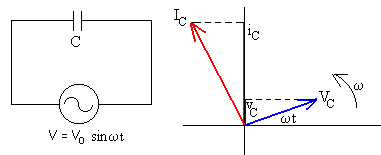
En un condensador la carga q, la capacidad C y diferencia de potencial v entre sus placas están relacionadas entre sí

q=C·v

Si se conecta las placas del condensador a un generador de corriente alterna

q=C·V₀·sin(ω t)

La intensidad se obtiene derivando la carga respecto del tiempo, i=dq/dt

$i_{C} = C ω V_{0} \cos (ω t) = C ω V_{0} \sin (ω t + \frac{π}{2})$

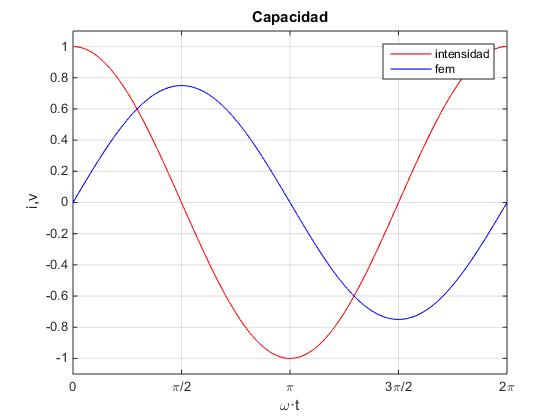
Para un condensador, la intensidad i_C está adelantada 90º respecto a la diferencia de potencial v_C. La relación ente sus amplitudes es

$I_{C} = C ω V_{C}$

con V_C=V₀, la amplitud de la fem alterna

Como V_C=-i·I_C/(ωC), definimos la impedancia Z_C de la capacidad

$Z_{C} = \frac{V_{C}}{I_{C}} = - i \frac{1}{ω C}$

Autoinducción

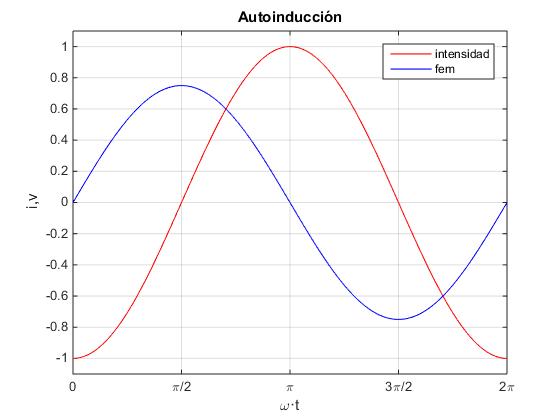
El script que ha servido para dibujar las tres gráficas es el siguiente. Basta modificar la fase de la intensidad (segunda línea) y el título de la gráfica.

wt=linspace(0,2*pi,200);
i=sin(wt-pi/2);
v=0.75*sin(wt);
plot(wt,i,'r',wt,v,'b');
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
axis([0,2*pi,-1.1,1.1])
legend('intensidad','fem')
xlabel('\omega·t')
ylabel('i,v')
title('Autoinducción')
grid on

Ya hemos estudiado la autoinducción y las corrientes autoinducidas que se producen en una bobina cuando circula por ella una corriente i variable con el tiempo.

La ecuación del circuito es (suma de fem igual a intensidad por resistencia), como que la resistencia es nula

$- L \frac{d i}{d t} + V_{0} \sin (ω t) = 0$

Integrando esta ecuación obtenemos i en función del tiempo

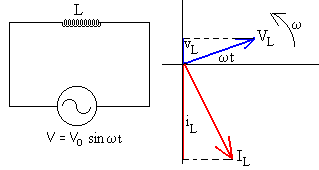
$i_{L} = - \frac{V_{0}}{ω L} \cos (ω t) = \frac{V_{0}}{ω L} \sin (ω t - \frac{π}{2})$

La intensidad i_L de la en la bobina está retrasada 90º respecto de la diferencia de potencial entre sus extremos v_L. La relación entre sus amplitudes es

$I_{L} = \frac{V_{L}}{ω L}$

con V_L=V₀, la amplitud de la fem alterna

Como V_L=iωL·I_L, definimos la impedancia Z_L de la autoinducción

$Z_{L} = \frac{V_{L}}{I_{L}} = i ω L$

Circuito LCR

El circuito LCR conectado a una fem alterna es análogo a las oscilaciones forzadas de un oscilador formado por una partícula unida a un muelle elástico, situado en un medio en el que la partícula experimenta una fuerza de rozamiento proporcional a la velocidad

En el apartado anterior, se ha estudiado el comportamiento de una bobina, un condensador y una resistencia cuando se conectan por separado a un generador de corriente alterna.

Estudiaremos el comportamiento de un sistema formado por los tres elementos dispuestos en serie y conectados a un generador de corriente alterna de amplitud V₀ y frecuencia angular ω .

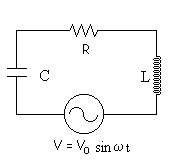
v=V₀ sin(ωt)

Dibujamos el diagrama de vectores teniendo en cuenta:

que la intensidad que pasa por todos los elementos es la misma,
que la suma (vectorial) de las diferencias de potencial entre los extremos de los tres elementos nos da la diferencia de potencial en el generador de corriente alterna.

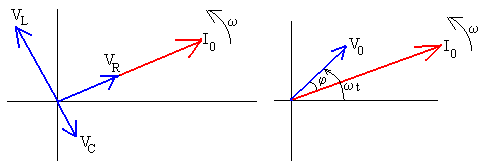
El vector resultante de la suma de los tres vectores es

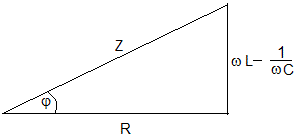
$V_{0} = \sqrt{V_{R}^{2} + {(V_{L} - V_{C})}^{2}} = I_{0} \sqrt{R^{2} + {(ω L - \frac{1}{ω C})}^{2}}$

Se denomina impedancia del circuito al término

$Z = \sqrt{R^{2} + {(ω L - \frac{1}{ω C})}^{2}}$

de modo que se cumpla una relación análoga a la de los circuitos de corriente continua

Intensidad

V₀=I₀·Z.

Representamos la amplitud de la intensidad I₀/(V₀/R) en función del cociente r=ω/ω₀, donde $ω_{0} = 1 / \sqrt{L C}$

$I_{0} = \frac{V_{0}}{\sqrt{R^{2} + {(ω L - \frac{1}{ω C})}^{2}}} = \frac{V_{0}}{R \sqrt{1 + {(\frac{ω L}{R} - \frac{1}{ω R C})}^{2}}} = \frac{V_{0}}{R} \frac{1}{\sqrt{1 + \frac{1}{R^{2}} \frac{L}{C} {(r - \frac{1}{r})}^{2}}}$

Denominamos k=L/(CR²)

k=25;
fplot(@(x) 1./sqrt(1+k*(x-1./x).^2),[0,2])
grid on
xlabel('\omega/\omega_0')
ylabel('I_0/(V_0/R)')
title('Amplitud de la intensidad')

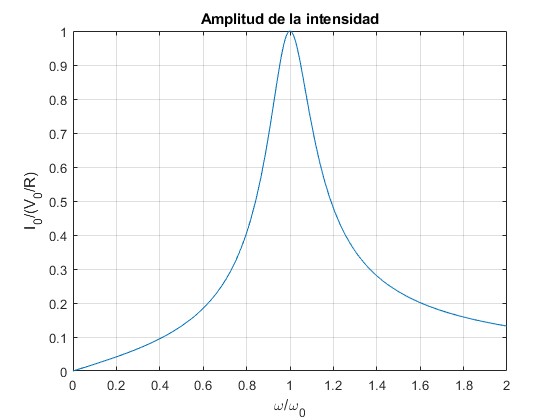
El máximo de la amplitud de la intensidad se produce para la frecuencia ω₀, para esta frecuencia la impedancia Z=R, la de un circuito con una única resistencia

Desfase

El ángulo que forma el vector resultante de longitud V₀ con el vector que representa la intensidad I₀ es

$\tan φ = \frac{V_{L} - V_{C}}{V_{R}} = \frac{ω L - \frac{1}{ω C}}{R}$

Representamos el desfase φ en función del cociente r=ω/ω₀

$\tan φ = \frac{1}{R} \sqrt{\frac{L}{C}} (r - \frac{1}{r})$

k=25;
fplot(@(x) atan(sqrt(k)*(x-1./x)),[0,2])
grid on
xlabel('\omega/\omega_0')
ylabel('\phi')
title('Desfase')

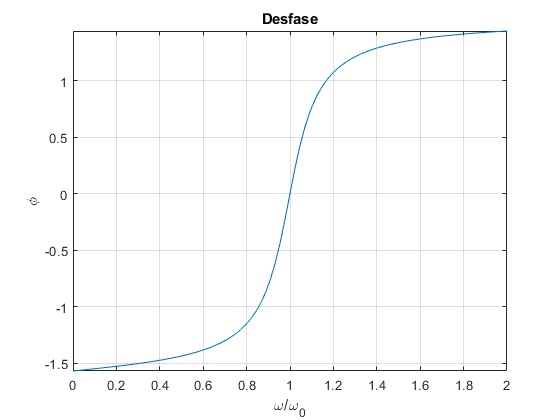
Para la frecuencia ω₀ el desfase φ=0, los efectos del condensador y de la autoinducción se compensan, por lo que la fem alterna se aplica de forma efectiva a la resistencia.

Las expresiones de la fem y de la intensidad del circuito son

$\begin{array}{l} v = V_{0} \sin (ω t) \\ i = I_{0} \sin (ω t - φ) \end{array}$

La intensidad de la corriente en el circuito está desfasada un ángulo φ respecto de la fem que suministra el generador.

Ejemplo:

R=1.5 Ω
L=5·10^-3 H
C=4·10^-6 F
ω=1.01·ω₀

La frecuencia propia del circuito es

$ω_{0} = \frac{1}{\sqrt{5 \cdot 10^{- 3} \cdot 4 \cdot 10^{- 6}}} = 7071 rad/s$

La frecuencia del generador es ω=1.01·ω₀=7142 rad/s

La impedancia vale

$Z = \sqrt{{1.5}^{2} + {(7142 \cdot 5 \cdot 10^{- 3} - \frac{1}{7142 \cdot 4 \cdot 10^{- 6}})}^{2}} = 1.65 Ω$

El desfase es

$\tan φ = \frac{7142 \cdot 5 \cdot 10^{- 3} - \frac{1}{7142 \cdot 4 \cdot 10^{- 6}}}{1.5} φ = 0.44 rad = 25.2 º$

Resonancia en un circuito LCR en serie

Estudiamos la condición de resonancia en las oscilaciones forzadas de una masa unida a un muelle elástico.

La potencia suministrada por el generador de corriente alterna es

P=i·v=V₀·I₀sin(ωt)·sin(ωt-φ)

P=V₀·I₀sin(ωt)·(sin(ωt)·cos φ-cos(ωt)·sinφ)=V₀·I₀(sin²(ωt)·cos φ-sin(ωt)·cos(ωt)·sinφ)

Esta magnitud es una función complicada del tiempo que no es útil desde el punto de vista práctico. Lo que tiene interés es el promedio de la potencia en un periodo 2π/ω.

=V₀·I₀(<sin²(ωt)>·cos φ-<sin(ωt)·cos(ωt)>·sinφ)

Se define como valor medio <f(t)> de una función periódica f(t) de periodo T a la integral

$< f (t) > = \frac{1}{T} \int_{0}^{T} f (t) \cdot d t$

El periodo de la función f(t)=sin²(ωt) es T=π/ω, su valor medio es

<sin²(ωt)>=1/2

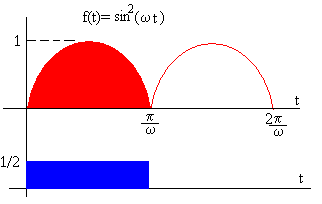
El área de color rojo es igual al área de color azul.

El periodo de la función f(t)=sin(ωt)·cos(ωt)=sin(2ωt)/2 es T=π/ω, su valor medio es

<sin(ωt)·cos(ωt)>=0

>> syms t T;
>> int('sin(2*pi*t/T)^2',0,T)/T
ans =1/2
>> int('sin(2*pi*t/T)*cos(2*pi*t/T)',0,T)/T
ans =0

Teniendo en cuenta estos resultados, el valor medio de la energía por unidad de tiempo, o potencia suministrada por el generador es

$ = \frac{1}{2} I_{0} V_{0} \cos φ$

El último término, cosφ se denomina factor de potencia.

El valor de es máximo cuando el ángulo de desfase φ es cero, para ello se tiene que cumplir que

$ω L = \frac{1}{ω C}$

es decir, la frecuencia ω del generador de corriente alterna debe coincidir con la frecuencia natural o propia ω₀ del circuito oscilante.

Cuando ω =ω₀ se cumple que

La intensidad de la corriente I₀ alcanza su valor máximo
La intensidad de la corriente en el circuito i y la fem v están en fase
La energía por unidad de tiempo  suministrada por el generador es máxima

Representamos la potencia media $\frac{}{(V_{0}^{2} / 2 R)}$ sumistrada por el generador, en función del cociente r=ω/ω₀

$\begin{array}{l} = \frac{1}{2} I_{0} V_{0} \cos φ = \frac{1}{2} \frac{V_{0}^{2}}{\sqrt{R^{2} + {(ω L - \frac{1}{ω C})}^{2}}} \frac{R}{\sqrt{R^{2} + {(ω L - \frac{1}{ω C})}^{2}}} = \\ \frac{1}{2} \frac{V_{0}^{2}}{R (1 + {(\frac{ω L}{R} - \frac{1}{ω C R})}^{2})} = \frac{V_{0}^{2}}{2 R} \frac{1}{1 + \frac{1}{R^{2}} \frac{L}{C} {(r - \frac{1}{r})}^{2}} \end{array}$

k=25;
f=@(x) 1./(1+k*(x-1./x).^2);
fplot(f,[0,2])
r1=(1/sqrt(k)+sqrt(1/k+4))/2;
r2=(-1/sqrt(k)+sqrt(1/k+4))/2;
line([r1,r1],[0,f(r1)],'lineStyle','--')
line([r2,r2],[0,f(r2)],'lineStyle','--')
line([0,2],[0.5,0.5])
grid on
xlabel('\omega/\omega_0')
ylabel('<P>/(V_0^2/2R)')
title('Potencia media')

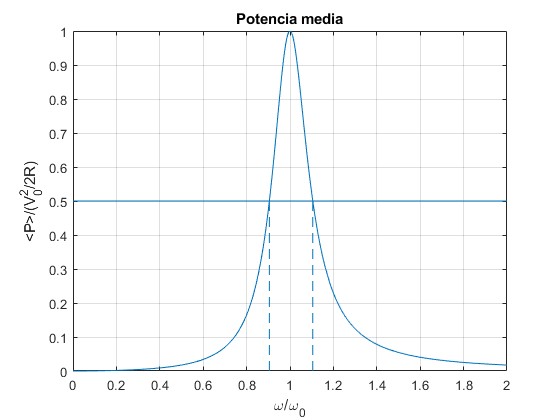
En la gráfica hemos señalado las frecuencias ω₁/ω₀ y ω₂/ω₀ para las cuales la potencia es la mitad de la máxima

$\begin{array}{l} \frac{1}{1 + k {(r - \frac{1}{r})}^{2}} = \frac{1}{2} \\ r - \frac{1}{r} = \pm \frac{1}{\sqrt{k}} \\ r_{1} = \frac{1}{2} (\frac{1}{\sqrt{k}} + \sqrt{\frac{1}{k} + 4}) \\ r_{2} = \frac{1}{2} (- \frac{1}{\sqrt{k}} + \sqrt{\frac{1}{k} + 4}) \end{array}$

son las raíces positivas de las dos ecuaciones de segundo grado

La anchura Δω=ω₂-ω₁ es

$\begin{array}{l} Δ r = r_{2} - r_{1} = \frac{1}{\sqrt{k}} = R \sqrt{\frac{C}{L}} \\ Δ ω = ω_{0} Δ r = \frac{1}{\sqrt{L C}} R \sqrt{\frac{C}{L}} = \frac{R}{L} \end{array}$

Los dos parámetros que caracterizan a esta curva son:

la frecuencia del máximo, $ω_{0} = \frac{1}{\sqrt{L C}}$ que es la frecuencia de resonancia y frecuencia natural del oscilador LC
La anchura, Δω=R/L

Referencias

Carl E. Mungan. An Elementary Introduction to Driven Damped Oscilltors . Resonance – Journal of Science Education, Volume 27, Issue 6