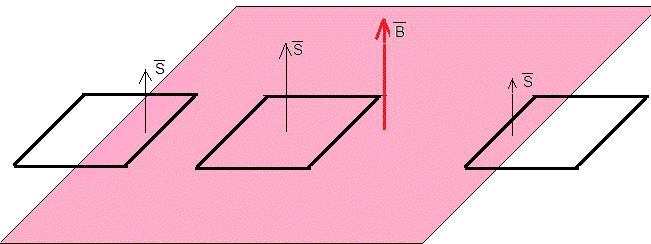
Una espira cuadrada de lado a, se mueve hacia una región rectangular de lado 2a en la que existe un campo magnético constante perpendicular al plano de la espira. Determinar la fem y el sentido de la corriente inducida en las siguientes situaciones

• Cuando la espira está entrando en dicha región (izquierda)
• Cuando está completamente introducida en la región en la que hay campo (centro)
• Cuando empieza a salir de dicha región (derecha)

Primera etapa

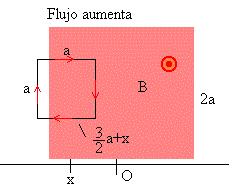
Supongamos que el campo magnético $\overrightarrow{B}$ es constante y es perpendicular al plano determinado por la espira. El flujo del campo magnético a través de la parte de la espira que se ha introducido en la región en la que existe el campo magnético es

${\displaystyle \Phi =\overrightarrow{B}·\overrightarrow{S}=Ba\left(\frac{3}{2}a+x\right),x<0}$

De acuerdo a la ley de Faraday, la fem inducida es

${\displaystyle V_E=-\frac{d\Phi }{dt}=-Ba\frac{dx}{dt}=-Bav}$

La derivada de x respecto del tiempo es la velocidad constante v>0 de la espira.

• Sentido de la corriente inducida

El flujo aumenta, al aumentar el área de la parte de la espira introducida en el campo magnético, el sentido de la corriente inducida es el de las agujas del reloj.

Si la resistencia de la espira es R, la intensidad de la corriente inducida es i=V_ε/R=vBa/R.

Segunda etapa

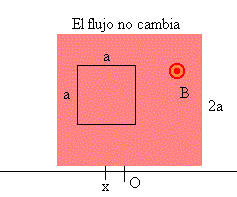
La espira se encuentra completamente introducida en la región en la que existe campo magnético uniforme.

${\displaystyle \Phi =\overrightarrow{B}·\overrightarrow{S}=B{a}^2}$

El flujo es constante, la fem es nula

V_ε=0

Tercera etapa

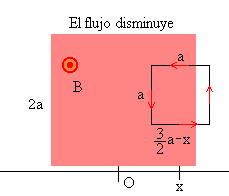
La espira empieza a salir del la región en la que existe campo magnético

El flujo del campo magnético a través de la parte de la espira que está introducida en dicho campo es

${\displaystyle \Phi =\overrightarrow{B}·\overrightarrow{S}=Ba\left(\frac{3}{2}a-x\right),x>0}$

De acuerdo a la ley de Faraday, la fem inducida es

${\displaystyle V_E=-\frac{d\Phi }{dt}=-Ba\frac{dx}{dt}=Bav}$

La derivada de x respecto del tiempo es la velocidad constante v>0 de la espira.

• Sentido de la corriente inducida

El flujo disminuye, al disminuir el área de la parte de la espira introducida en el campo magnético, el sentido de la corriente inducida es el contrario al de las agujas del reloj.

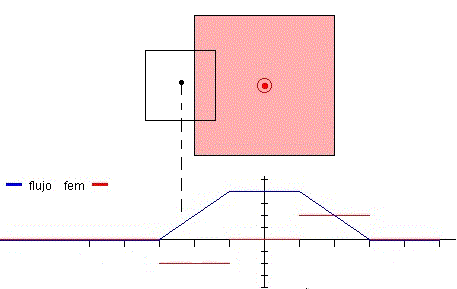
Representamos el flujo (azul) y la fem (rojo) en función de la posición del centro de la espira medida desde un origen situado en el centro de la región en la que existe campo magnético. Observaremos que:

• Cuando el flujo es constante la fem es nula
• Cuando el flujo aumenta (pendiente positiva) la fem es negativa
• Cuando el flujo disminuye (pendiente negativa) la fem es positiva

Actividades

Se introduce

• El campo magnético (en gauss), que es un número positivo o negativo.
• La velocidad de la varilla (en cm/s), un número positivo menor que 10.

Se pulsa el botón titulado Nuevo

El sentido de la corriente inducida, es decir, el movimiento de los portadores de carga positiva se representa por pequeños círculos de color rojo.

Observaremos que solamente hay flujo a través de la porción del área de la espira sombreada de color gris claro, en cuyo centro hemos situado el vector campo magnético (flecha de color azul).

Ejemplo

• Sea el valor del campo magnético B, 40 gauss= 40·10^-4 T
• La velocidad, v=5 cm/s=0.05 m/s
• La dimensión de la espira, a=10 cm =0.1 m está fijada en el programa

El valor de la fem inducida es V_ε=2·10^-5 voltios

Movimiento de la espira

Como en el caso de una varilla que se mueve en un campo magnético uniforme. Es necesario ejercer una fuerza F_a sobre la varilla para que se mueva con velocidad constante. Esta fuerza es igual y de sentido contrario a la fuerza que ejerce el campo magnético sobre la porción de corriente rectilínea de longitud L por la que circula una corriente i.

${\displaystyle \overrightarrow{F_m}=i({\widehat{u}}_t\times \overrightarrow{B})L}$

El vector unitario ${\widehat{u}}_t$ que señala el sentido de la corriente y el campo $\overrightarrow{B}$ son mutuamente perpendiculares, la longitud del conductor es a, por lo que el módulo de la fuerza magnética es F_m=iBa, donde la intensidad de la corriente inducida es i=vBa/R

${\displaystyle F_m=\frac{B^2{a}^2}{R}v}$

Movimiento uniforme

• Primera etapa



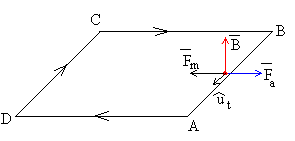
Cuando la espira penetra en el campo magnético, sobre el lado AB el campo magnético ejerce una fuerza F_m=iBa, dirigida hacia la izquierda (de sentido contrario al movimiento).

Para mantener la velocidad constante tendremos que aplicar una fuerza igual y de sentido contrario F_a dirigida hacia la derecha.

• Segunda etapa

Como no hay corriente inducida, la fuerza magnética sobre la espira es cero y en ausencia de rozamiento, no es necesario aplicar ninguna fuerza.

• Tercera etapa



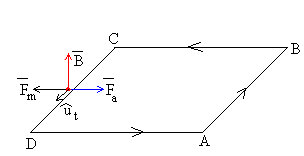
El lado CD está en el interior del campo magnético uniforme. La fuerza que ejerce el campo magnético sobre esta porción de conductor es F_m=iBa y está dirigida hacia la izquierda (en sentido contrario al del movimiento).

Para mantener la velocidad constante tendremos que aplicar una fuerza igual y de sentido contrario F_a dirigida hacia la derecha.

Como en el caso de la varilla que se desplaza en un campo magnético uniforme, se puede demostrar de forma análoga, que la energía por unidad de tiempo suministrada por la fuerza mecánica F_a, se disipa en la resistencia de la espira por efecto Joule.

Movimiento no uniforme

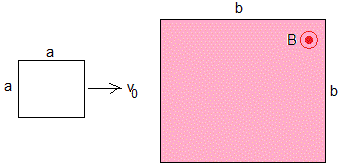
En una región cuadrada de lado b, existe un campo magnético uniforme perpendicular al plano del dibujo. Una espira cuadrada de lado a<b y resistencia R se dirige hacia esta región con velocidad v₀. Vamos a determinar el movimiento de la espira.

En la figura, se muestra la fuerza sobre la espira cuando entra y cuando sale de la región donde existe campo magnético. Son de sentido contrario a la velocidad de la espira

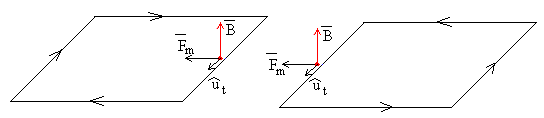
La ecuación del movimiento es

${\displaystyle m\frac{dv}{dt}=-\frac{B^2{a}^2}{R}v}$

Expresamos la velocidad de la espira v en función de la posición x

${\displaystyle \begin{array}{l}\frac{dv}{dx}\frac{dx}{dt}=-kv,k=\frac{B^2{a}^2}{mR}\\ \frac{dv}{dx}=-k\\ v-v_0=-k(x-x_0)\end{array}}$

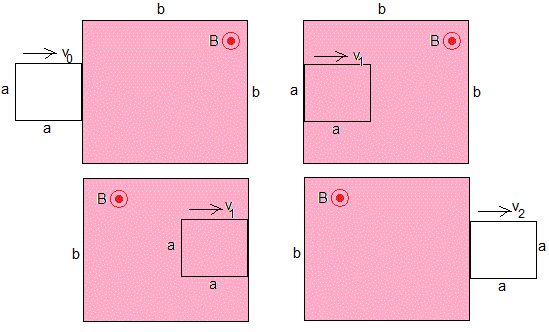
• la espira entra

${\displaystyle v_1-v_0=-ka}$

• la espira sale

${\displaystyle v_2-v_1=-ka}$

En la figura, se muestra la velocidad v de la espira en función de la posición x

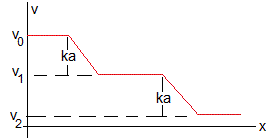
Para que atraviese la región donde existe campo magnético, la velocidad inicial v₀ mínima se obtiene poniendo v₂=0

${\displaystyle \begin{array}{l}{v}_0=2ka=2\frac{B^2{a}^3}{mR}\\ v_1=ka=\frac{B^2{a}^3}{mR}\end{array}}$

El tiempo que tarda la espira en entrar en la región donde existe campo magnético, se calcula expresando la velocidad de la espira en función del tiempo

${\displaystyle \begin{array}{l}\frac{dv}{dt}=-kv\\ {\displaystyle \underset{v_0}{\overset{v}{\int }}\frac{dv}{v}}=-k{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ \ln \frac{v}{v_0}=-kt\\ t_1=-\frac{1}{k}\ln \frac{v_1}{v_0}=-\frac{1}{k}\ln \frac{1}{2}=\frac{mR}{B^2{a}^2}\ln 2\end{array}}$

Referencias

Physics Challenge for Teachers and Students. Solution to May 2016 Challenge. The mystery of May B. The Physics Teacher. Vol. 54, 2016, pp. 277