Consideremos un bucle de radio R, la velocidad inicial de la partícula es v₀ en la posición inicial θ=0. Vamos a calcular la velocidad v de la partícula en la posición θ.

La energía inicial de la partícula es

${\displaystyle E_0=\frac{1}{2}m{v}_0^2}$

La energía de la partícula en la posición θ es

${\displaystyle E=\frac{1}{2}m{v}^2+mgR(1-\cos \theta )}$

El trabajo de la fuerza de rozamiento a lo largo del camino de longitud R·θ es

${\displaystyle W=-{\displaystyle \underset{0}{\overset{R\theta }{\int }}\mu N·ds}=-{\displaystyle \underset{0}{\overset{\theta }{\int }}\mu N·R}·d\theta }$

El trabajo W de la fuerza de rozamiento disminuye la energía E de la partícula. W=E-E₀

La ecuación del movimiento en la dirección radial nos proporciona el valor de la reacción N de la pista circular

${\displaystyle m\frac{v^2}{R}=N-mg\cos \theta }$

Se sustituye N en la expresión del trabajo de la fuerza de rozamiento

${\displaystyle W=-{\displaystyle \underset{0}{\overset{\theta }{\int }}\mu m\left(v^2+gR\cos \theta \right)}d\theta =-\mu m\left({\displaystyle \underset{0}{\overset{\theta }{\int }}{v}^2}d\theta +gR\sin \theta \right)}$

La velocidad v de la partícula en función de la posición θ

${\displaystyle \begin{array}{l}-\mu m\left({\displaystyle \underset{0}{\overset{\theta }{\int }}{v}^2}d\theta +gR\sin \theta \right)=\frac{1}{2}m{v}^2+mgR(1-\cos \theta )-\frac{1}{2}m{v}_0^2\\ \frac{v^2}{gR}=\frac{v_0^2}{gR}+2(\cos \theta -\mu \sin \theta -1)-2\mu {\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{v^2}{gR}d\theta }\end{array}}$

o bien, en términos de la velocidad adimensional V

${\displaystyle V^2=V_0^2+2(\cos \theta -\mu \sin \theta -1)-2\mu {\displaystyle \underset{0}{\overset{\theta }{\int }}{V}^{2}d\theta }}$

De acuerdo con el artículo citado en las referencias esta ecuación tiene solución analítica por ser de la forma

${\displaystyle V^2(\theta )=f(\theta )+{\displaystyle \underset{0}{\overset{\theta }{\int }}h(t)·V^2(t)·dt}}$

denominada integral de Volterra. La solución se obtiene en dos pasos

${\displaystyle \begin{array}{l}R(\theta ,t)=h(t)\exp \left({\displaystyle \underset{t}{\overset{\theta }{\int }}h(s)·ds}\right)\\ V^2(\theta )=f(\theta )+{\displaystyle \underset{0}{\overset{\theta }{\int }}R(\theta ,t)}·f(t)·dt\end{array}}$

Donde h(t)=-2μ

$$\begin{gathered} {\displaystyle \begin{array}{l}R(\theta ,t)=-2\mu \exp \left({\displaystyle \underset{t}{\overset{\theta }{\int }}-2\mu ·ds}\right)=-2\mu \exp \left(-2\mu \theta \right)·\exp \left(2\mu t\right)\\ f(t)=V_0^2+2\left(\cos t-\mu \sin t-1\right)\\ V^2(\theta )=V_0^2+2\left(\cos \theta -\mu \sin \theta -1\right)- \\ 2\mu \exp \left(-2\mu \theta \right){\displaystyle \underset{0}{\overset{\theta }{\int }}\exp \left(2\mu t\right)\left(V_0^2+2\left(\cos t-\mu \sin t-1\right)\right)}dt\end{array}} \end{gathered}$$

Posición final de la partícula en la pista circular

Integrando por partes y simplificando, despejamos la velocidad adimensional V en función de la la posición θ

${\displaystyle V^2=\left(V_0^2+\frac{2\left(2{\mu }^2-1\right)}{1+4{\mu }^2}\right)\exp \left(-2\mu \theta \right)-\frac{2}{1+4{\mu }^2}\left(\left(2{\mu }^2-1\right)\cos \theta +3\mu \sin \theta \right)}$

Esta junto con la ecuación del movimiento en la dirección radial

${\displaystyle \frac{N}{mg}=V^2+\cos \theta }$

determinan la posición final de la partícula en la pista circular. La reacción de la pista deberá ser N>0 para que la partícula permanezca en contacto con la pista y no caiga

• Para 0<θ<π/2 y para 3π/2<θ<2pi, cosθ>0, por lo que siempre se cumple que N>0

Si no hubiera rozamiento, μ=0, la velocidad mínima V₀ para que llegue a θ=π/2 sería

${\displaystyle V_0^2=2}$

• para π/2<θ<3π/2, cosθ<0, la partícula tiene una velocidad no nula en el momento en el que empieza a perder el contacto con la pista, N=0

Si no hubiera rozamiento μ=0, el ángulo θ para el cual N=0 sería

${\displaystyle \begin{array}{l}0=V^2+\cos \theta \\ 0=V_0^2-2+2\cos \theta +\cos \theta \\ \cos \theta =-\frac{1}{3}\left(V_0^2-2\right)\end{array}}$

La velocidad inicial V₀ mínima para que la partícula describa el bucle se obtiene con θ=π

${\displaystyle V_0^2=5}$

Ejemplos

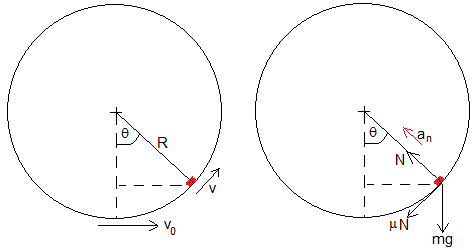
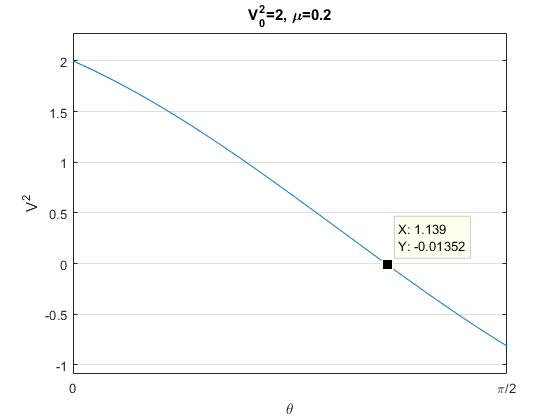
1. En el script, la variable V2 guarda la expresión de la velocidad adimensional V² en términos de V₀, μ y θ en el código V0, mu y x . La variable VV2 guarda dicha expresión para el caso particular de μ=0.2 y V₀²=2. Representamos gráficamente VV2 función de x y vemos que velocidad V² se hace cero para el ángulo θ=1.132=64.8º, resultado que obtenemos con mejor aproximación mediante la función solve.

syms V0 mu x t;
V2=V0^2+2*(cos(x)-mu*sin(x)-1)-2*mu*exp(-2*mu*x)*
int('(V0^2+2*(cos(t)-mu*sin(t)-1))*exp(2*mu*t)',t,0,x);
V2=simplify(V2);
VV2=subs(V2,{V0,mu},{sqrt(2),0.2});
double(solve(VV2,x)*180/pi)
ezplot(VV2,[0,pi/2])
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
grid on
title('V_0^2=2, \mu=0.2')
xlabel('\theta')
ylabel('V^2')

ans =   64.8741



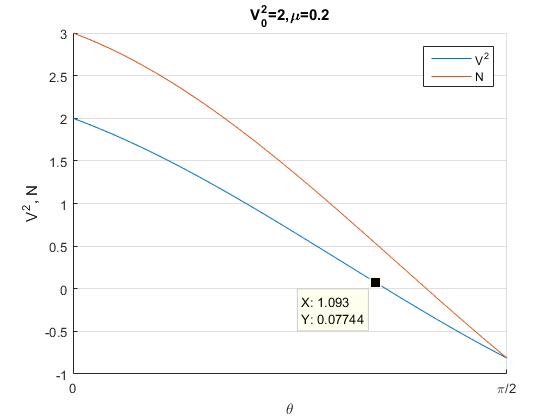
2. Comprobamos que la larga integración y simplificación realizada a mano, coincide con la obtenida con MATLAB Symbolic Toolbox en el ejemplo 1. Representamos V² en función de θ para μ=0.2 y V₀²=2 y también se representa la reacción N. Vemos que la velocidad V² se hace cero antes de que lo haga N. Con fzero calculamos el angulo θ=64.87 para el cual la velocidad se anula, V²=0.

mu=0.2;
V0=sqrt(2);
V2=@(mu,x) (V0^2+2*(2*mu^2-1)/(1+4*mu^2))*exp(-2*mu*x)
-2*((2*mu^2-1)*cos(x)+3*mu*sin(x))/(1+4*mu^2);
hold on
f=@(x) V2(0.2,x);
fzero(f,pi/2)*180/pi
fplot(f,[0,pi/2])
f=@(x) V2(0,x);
fplot(f,[0,pi/2])
hold off
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
legend('\mu=0.2','\mu=0');
grid on
title('V_0^2=2')
xlabel('\theta')
ylabel('V^2') 

ans =   64.8741



3. Cambiamos el valor de la velocidad inicial V₀²=5, con el mismo rozamiento, μ=0.2. En este caso la normal N se hace cero antes de que lo haga la velocidad V²

mu=0.2;
V0=sqrt(5);
V2=@(mu,x) (V0^2+2*(2*mu^2-1)/(1+4*mu^2))*exp(-2*mu*x)
-2*((2*mu^2-1)*cos(x)+3*mu*sin(x))/(1+4*mu^2);
hold on
f=@(x) V2(0.2,x)+cos(x);
fzero(f,[pi/2,pi])*180/pi
fplot(f,[0,pi])
f=@(x) V2(0.2,x);
fplot(f,[0,pi])
hold off
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
legend('N','V^2');
grid on
title('V_0^2=2, \mu=0.2')
xlabel('\theta')
ylabel('N, V^2') 

ans =   104.4372



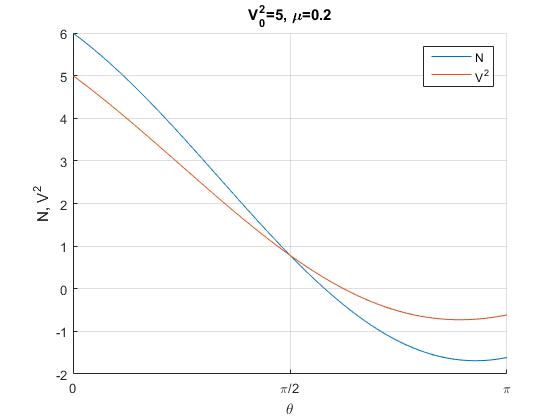
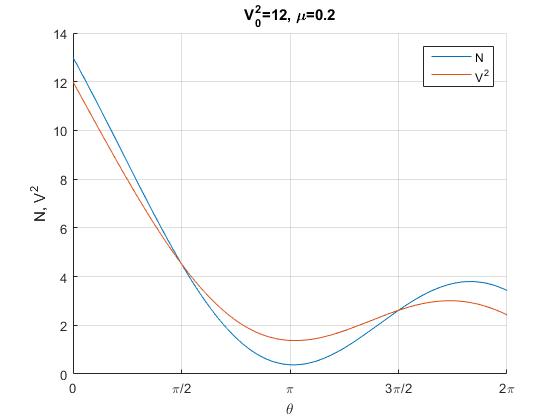
4. Vamos cambiando el valor de la velocidad inicial V₀² con el mismo rozamiento, μ=0.2 y vamos observando si se hace cero antes V² o N. Por ejemplo, para V₀²=12, no se hace cero ni V² ni N en el intervalo [0,2π]. Cambiando los valores de V₀ y μ y observando la representación gráfica de V² y N nos permite conocer con detalle la complejidad del movimiento de la partícula en el bucle

mu=0.2;
V0=sqrt(12);
V2=@(mu,x) (V0^2+2*(2*mu^2-1)/(1+4*mu^2))*exp(-2*mu*x)-
2*((2*mu^2-1)*cos(x)+3*mu*sin(x))/(1+4*mu^2);
hold on
f=@(x) V2(0.2,x)+cos(x);
fplot(f,[0,2*pi])
f=@(x) V2(0.2,x);
fplot(f,[0,2*pi])
hold off
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
legend('N','V^2');
grid on
title('V_0^2=12, \mu=0.2')
xlabel('\theta')
ylabel('N, V^2') 

Ecuación diferencial del movimiento

A partir de la figura al principio de esta página, en la que se han dibujado las fuerzas sobre la partícula, formulamos las ecuaciones del movimiento en la dirección radial y tangencial

${\displaystyle \begin{array}{l}mR{\left(\frac{d\theta }{dt}\right)}^2=N-mg\cos \theta \\ mR\frac{d^2\theta }{d{t}^2}=-mg\sin \theta -\mu N\end{array}}$

Eliminando la reacción N

${\displaystyle \frac{d^2\theta }{d{t}^2}=-\frac{g}{R}\sin \theta -\mu \frac{g}{R}\cos \theta -\mu {\left(\frac{d\theta }{dt}\right)}^2}$

Se resuelve esta ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, θ=0, dθ/dt=v₀/R

mu=0.2;  %coeficiente de rozamiento
R=1; %radio
x0=[0, sqrt(5*9.8)];
f=@(t,x) [x(2);-(9.8/R)*sin(x(1))-(mu*9.8/R)*cos(x(1))-mu*x(2)^2];
tspan=[0 2.2];
opts=odeset('events',@stop_bucle);
[t,x]=ode45(f,tspan,x0,opts);
 
subplot(2,1,1)
plot(t,x(:,1))
set(gca,'YTick',0:pi/2:2*pi)
set(gca,'YTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
grid on
xlabel('t')
ylabel('\theta');
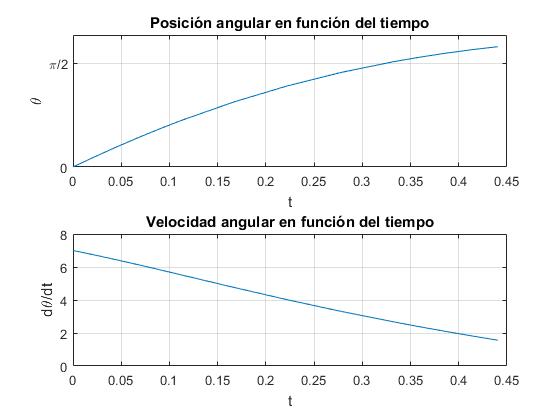
title('Posición angular en función del tiempo')
subplot(2,1,2)
plot(t,x(:,2))
grid on
xlabel('t')
ylabel('d\theta/dt');
title('Velocidad angular en función del tiempo')

Se crea una función que detiene el proceso de integración cuando la velocidad dθ/dt=0 o cuando la reacción N sea cero, en los cuadrantes apropiados

function [detect,stopin,direction]=stop_bucle(~,x)
   ang=mod(x(1),2*pi); 
    if (ang>0 && ang<pi/2) ||(ang>pi && ang<2*pi)  
        detect=x(2);
    else
        detect=x(2)^2/9.8+cos(x(1));
    end
    stopin=1; 
    direction=-1; 
end

En la figura, repetimos el ejemplo 3, vemos que el proceso de integración se detiene en el segundo cuadrante, cuando N=0, anque dθ/dt sea mayor que cero. En ese instante, la partícula deja de tener contacto con la pista circular y describe una trayectoria parabólica de caída.

Actividades

Se introduce

• El coeficiente cinético de rozamiento, μ_k en el control titulado Coeficiente cinético
• La velocidad inicial v₀, multiplicada por $\sqrt{9.8}$ en el control titulado Velocidad inicial
• Se ha fijado el radio de la pista circular R=1

Se pulsa el botón titulado Nuevo y se observa el movimiento del bloque

En la parte izquierda, se proporcionanlos datos del tiempo t, la posición angular θ, en grados, la velocidad angular ω=dθ/dt, y la reacción N

• Cuando la velocidad ω es cero, el cuerpo se detiene, luego, iniciaría el movimiento de vuelta. Este movimiento se describe con detalle en la página titulada Movimiento sobre una superficie semicircular cóncava
• Cuando la reacción N es nula, el cuerpo describe una trayectoria parabólica.

En la parte derecha, se representa el balance energético: la energía cinética (en color rojo), la energía potencial (en color azul) y el trabajo de la fuerza de rozamiento (en color negro)

Referencias

Waldemar Klobus. Motion on a vertical loop with friction. Am. J. Phys. 79 (9), September 2011, pp. 913-918