Transformada inversa de Laplace
Las transformadas de Laplace de las funciones que hemos estudiado en esta página se resumen en la tabla siguiente:
| f(t) | |
|---|---|
| c1f1(t)+c2f2(t) | c1F1(s)+c2F2(s) |
| exp(a·t) | |
| cos(ωt) | |
| sin(ωt) | |
| tn | |
exp(at)·f(t) exp(at)·cos(ωt) |
F(s-a)
|
| u(t-a) | exp(-as)/s |
| u(t-a)·f(t-a) | exp(-as)·F(s) |
| δ(t-a) | exp(-as) |
| f'(t) (derivada primera) | s·F(s)-f(0) |
| f''(t) (derivada segunda) | s2·F(s)-s·f(0)-s·f'(0) |
| (integral) | F(s)/s |
| f(t)=f(t+p), (función periódica) | |
| f(at) | |
| tnf(t) |
Como vimos en la página Fracciones polinómicas, la función
1.-Raíces reales distintas
Expresamos la primera fracción en términos de la variable s en vez de x, y sustituímos los decimales periódicos por las fracciones equivalentes.
Como vemos en la tabla, la transformada inversa de Laplace se escribe
f(t)=exp(3t)/15-2·exp(-2t)/5+1/3
Obtenemos una expresión similar empleando la función MATLAB
>> syms s; >> fs=(s-2)/(s^3-s^2-6*s); >> ft=ilaplace(f) ft =exp(3*t)/15 - 2/(5*exp(2*t)) + 1/3
2.-Raíces complejas distintas
Como vemos en la tabla, la transformada inversa de Laplace se escribe
f(t)=-3·exp(-t)·cos(t)-4·exp(-t)sin(t)+4·exp(-t)=(4-3·cos(t)-4·sin(t))·exp(-t)
No es necesario sumar las dos fracciones con las raíces conjugadas para convertirla en una única fracción racional
si creamos una nueva entrada en la tabla de las transformadas inversas de Laplace. Sea
Como vemos en la tabla, la transformada inversa de Laplace se escribe
Con c=-1.5, d=2, a=-1, b=1, obtenemos
f(t)=(2·exp(-t))(-1.5·cos(t)-2·sin(t))+4·exp(-t))=(4-3·cos(t)-4·sin(t))·exp(-t)
>> syms s; >> fs=(s^2-2*s+1)/(s^3+3*s^2+4*s+2); >> ft=ilaplace(fs) ft =4/exp(t) - (3*(cos(t) + (4*sin(t))/3))/exp(t) >> simplify(ft) ans =-(3*cos(t) + 4*sin(t) - 4)/exp(t)
3.-Raíces repetidas
Como vemos en la tabla, la transformada inversa de Laplace se escribe
f(t)=exp(2t)-exp(-t)+2t·exp(-t)
>> syms s; >> fs=(5*s-1)/(s^3-3*s-2); >> ft=ilaplace(fs) ft =exp(2*t) - 1/exp(t) + (2*t)/exp(t)
4.-Fracciones impropias
Como vemos en la tabla, la transformada inversa de Laplace se escribe
f(t)=δ(t)+-6·exp(-3t)/5+11·exp(2t)/5
>> syms s; >> fs=(s^2+2*s+3)/(s^2+s-6); >> ft=ilaplace(fs) ft =(11*exp(2*t))/5 - 6/(5*exp(3*t)) + dirac(t)
Ejercicios
Descomponer una fracción en suma de fracciones más simples mediante
Ecuaciones diferenciales lineales
1.-Vamos a utilizar la transformada de Laplace para calcular la solución de la ecuación diferencial con las condiciones iniciales especificadas.
Transformamos la fracción racional F(s) en suma de fracciones más simples, factorizando el denominador y aplicamos la transformada inversa de Laplace
>> syms s;
>> Fs=(3*s+13)/(s^2+4*s+3);
>> x=ilaplace(Fs)
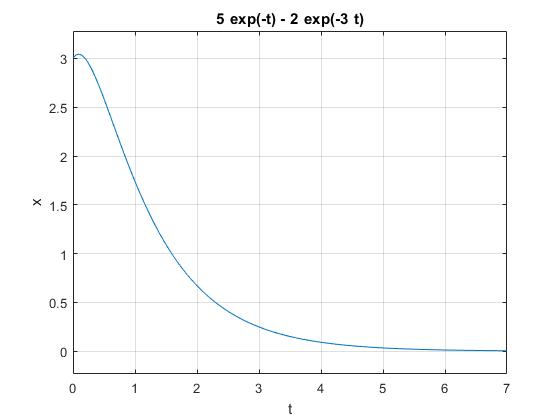
x =5/exp(t) - 2/exp(3*t)
>> ezplot(x,[0,7])
>> grid on
>> xlabel('t')
>> ylabel('x')
2.-Resolver la ecuación diferencial con las condiciones iniciales especificadas
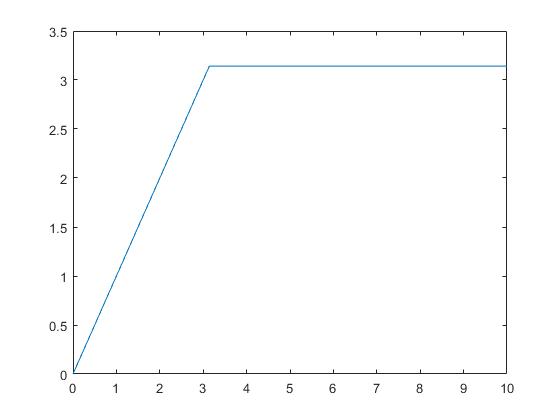
g(t)=(u(t-0)-u(t-π))·t+u(t-π)·π=t-(t-π)·u(t-π)
>> g=@(t) t+(pi-t).*heaviside(t-pi); >> fplot(g,[0,10])
La transformada de Laplace es
Expresamos la fracción en suma de fracciones más simples y calculamos la transformada inversa de Laplace
>> syms s;
>> Fs=(1-exp(-sym('pi')*s))/(s^2*(s^2+4));
>> x=ilaplace(Fs)
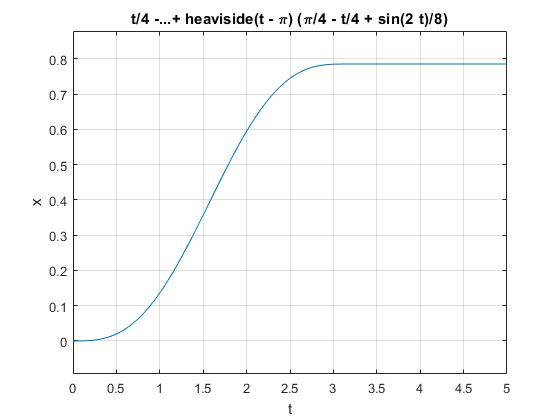
x =t/4 - sin(2*t)/8 + heaviside(t - pi)*(pi/4 - t/4 + sin(2*t)/8)
>> ezplot(x,[0,5])
>> grid on
>> xlabel('t')
>> ylabel('x')
3.-Resolvemos la ecuación diferencial, con las condiciones iniciales especificadas
Representa una masa unida a un muelle elástico que está en reposo, sin deformar. La función delta describe un impulso unidad en el instante t=2. La transformada de Laplace de la ecuación diferencial con las condiciones iniciales especificadas es
Teniendo en cuenta que la transformada de sin(2πt) es
y la propiedad de la función u(t-a). Escribimos F(s)
La solución es
>> syms s;
>> Fs=exp(-2*s)*2*sym('pi')/(2*sym('pi')*(s^2+4*sym('pi')^2));
>> x=ilaplace(Fs)
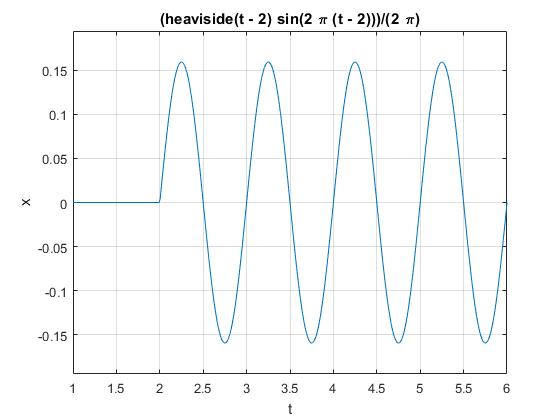
x =(heaviside(t - 2)*sin(2*pi*(t - 2)))/(2*pi)
>> ezplot(x,[1,6])
>> grid on
>> xlabel('t')
>> ylabel('x')
4.-Resolvemos la ecuación diferencial, con las condiciones iniciales especificadas
Se le aplica a un oscilador en reposo una fuerza oscilante durante 2 unidades de tiempo
Escribimos la función f(t) de la forma apropiada
La trasnformada de la ecuación diferencial con las condiciones iniciales especificadas es
Teniendo en cuanta la propiedad de u(t-a), la solución será de la forma x(t)=u(t-0)·g(t-0)-u(t-2)·g(t-2)=g(t)-u(t-2)·g(t-2). Calculamos g(t). La fracción
La función g(t) es
La solución de la ecuación diferencial x(t)
>> syms s;
>> Fs=(1-exp(-2*s))*s/((s^2+1)*(s^2+sym('pi')^2));
>> x=ilaplace(Fs);
>> pretty(x)
/ cos(pi (t - 2)) cos(t - 2) \
heaviside(t - 2) | ----------------- - ----------------- |
\ (pi - 1) (pi + 1) (pi - 1) (pi + 1) /
cos(pi t) cos(t)
- ----------------- + -----------------
(pi - 1) (pi + 1) (pi - 1) (pi + 1)
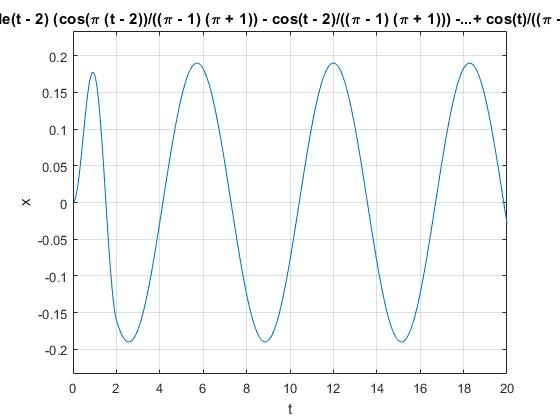
>> ezplot(x,[0,20])
>> grid on
>> xlabel('t')
>> ylabel('x')
Sistema de dos ecuaciones diferenciales
Sea el sistema de dos ecuaciones diferenciales lineales de primer orden con coeficientes constantes que estudiamos en la página Sistema no homogéneo de ecuaciones diferenciales.
Aplicamos la transformada de Laplace a cada una de las ecuaciones y tenemos en cuenta las condiciones iniciales, es decir, el valor inicial x(0) e y(0) en el instante t=0
Resolvemos el sistema de dos ecuaciones con dos incógnitas, despejando X(s) e Y(s) mediante el operador división por la izquierda. Calculamos la transformada inversa de Laplace mediante la función
>> syms s; >> A=[(s+2),4;1,(s-1)]; >> b=[1/s+4/s^2;1+3/s^3]; >> X=A\b X = -(3*s^3 - 3*s^2 + 4*s + 12)/(s^3*(s^2 + s - 6)) (s^4 + 2*s^3 - s^2 - s + 6)/(s^3*(s^2 + s - 6)) >> ilaplace(X) ans = t - (4*exp(2*t))/5 + 4/(5*exp(3*t)) + t^2 (4*exp(2*t))/5 + 1/(5*exp(3*t)) - t^2/2
Obtenemos el mismo resultado que con la función