Funciones armónicas

En primer lugar, vamos a distinguir entre las magnitudes: amplitud A, frecuencia f y fase φ en la función armónica

x=Asin(2πf·t+φ).

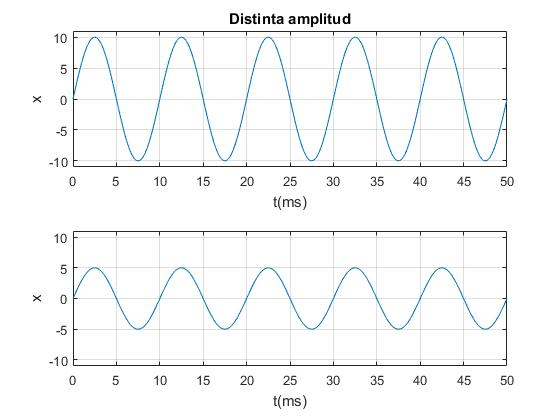
• Dos amplitudes distintas, A=10 y A=5 y la misma frecuencia f=100 Hz, (el tiempo se mide en milisegundos, ms)

subplot(2,1,1)
x=@(t) 10*sin(2*pi*0.1*t); %amplitud 10
fplot(x,[0,50])
xlabel('t(ms)')
ylabel('x')
title('Distinta amplitud')
ylim([-11,11])
grid on

subplot(2,1,2)
x=@(t) 5*sin(2*pi*0.1*t); %amplitud 5
fplot(x,[0,50])
ylim([-10,10])
xlabel('t(ms)')
ylabel('x')
ylim([-11,11])
grid on

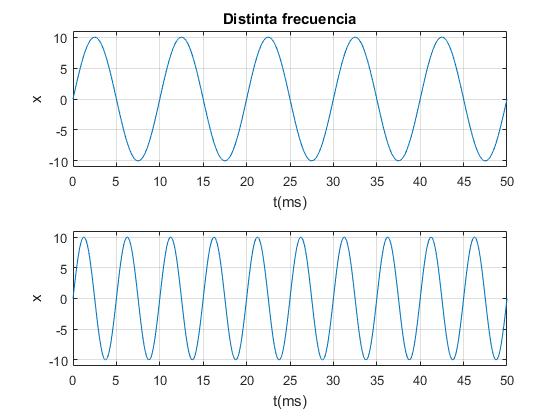
• La misma amplitud A=10, dos frecuencias distintas f=100 y f=200 Hz

subplot(2,1,1)
x=@(t) 10*sin(2*pi*0.1*t); %frecuencia, 100 Hz
fplot(x,[0,50])
xlabel('t(ms)')
ylabel('x')
title('Distinta frecuencia')
ylim([-11,11])
grid on

subplot(2,1,2)
x=@(t) 10*sin(2*pi*0.2*t);  %frecuencia, 200 Hz
fplot(x,[0,50])
xlabel('t(ms)')
ylabel('x')
ylim([-11,11])
grid on

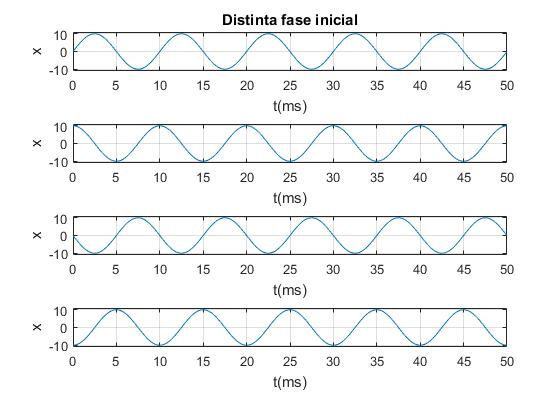
• Fases iniciales distintas: 0, π/2, π,3π/2, misma frecuencia f=100 Hz y misma amplitud A=10

subplot(4,1,1)
x=@(t) 10*sin(2*pi*0.1*t);
fplot(x,[0,50])
xlabel('t(ms)')
ylabel('x')
title('Distinta fase inicial')
ylim([-11,11])
grid on

subplot(4,1,2)
x=@(t) 10*sin(2*pi*0.1*t+pi/2);
fplot(x,[0,50])
xlabel('t(ms)')
ylabel('x')
ylim([-11,11])
grid on

subplot(4,1,3)
x=@(t) 10*sin(2*pi*0.1*t+pi);
fplot(x,[0,50])
xlabel('t(ms)')
ylabel('x')
ylim([-11,11])
grid on

subplot(4,1,4)
x=@(t) 10*sin(2*pi*0.1*t+3*pi/2);
fplot(x,[0,50])
xlabel('t(ms)')
ylabel('x')
ylim([-11,11])
grid on

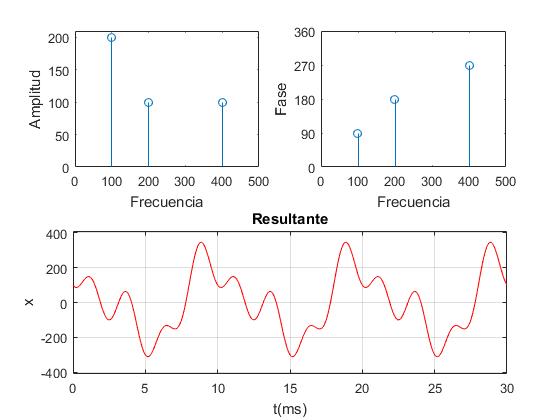
• Una función periódica resultado de la superposición de tres funciones armónicas con distintas frecuencias, amplitudes y fases iniciales

x=200sin(2πf·100+π/2)+100sin(2πf·200+π)+100sin(2πf·400+3π/2)

f=[100,200,400]; %frecuencias
A=[200,100,100]; %amplitudes
phi=[90,180,270]; %fases

subplot(2,2,1)
stem(f,A)
axis([0,500,0,210])
xlabel('Frecuencia')
ylabel('Amplitud')

subplot(2,2,2)
stem(f,phi)
axis([0,500,0,360])
xlabel('Frecuencia')
set(gca,'YTick',0:90:360)
set(gca,'YTickLabel',{'0',90','180','270','360'})
ylabel('Fase')

subplot(2,2,3:4) %resultante
t=(0:0.1:30)/1000; %milisegundos
x=zeros(1,length(t));
for i=1:length(f)
    x=x+A(i)*sin(2*pi*f(i)*t+phi(i)*pi/180);
end
plot(t,x,'r')
xlabel('t(ms)')
ylabel('x')
title('Resultante')
ylim([-410,410])
set(gca,'XTick',(0:5:30)/1000)
set(gca,'XTickLabel',{'0','5','10','15','20','25','30'})
grid on

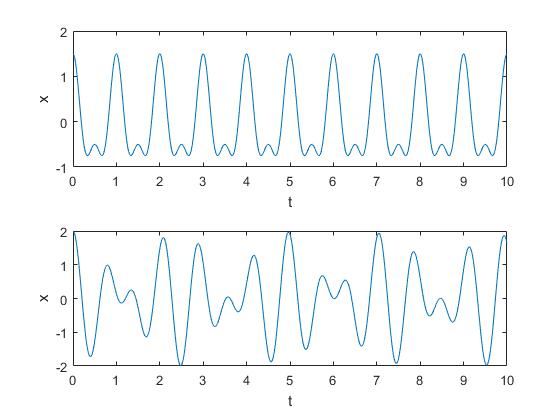
Función periódica

Una función es periódica de periodo P si hay un número P>0 tal que f(t+P)=f(t). Cualquier múltiplo n entero de P es también periodo f(t+nP)=f(t)

La función f(t)=cos(2πt)+cos(4πt)/2, es la suma de dos funciones periódicas de periodos 1 y 0.5, respectivamente. Como vemos en la gráfica f(t) es periódica con periodo P=1.

Las funciones cos(t) y $\cos \left(\sqrt{2}t\right)$ son periódicas de periodo 2π y $2\pi /\sqrt{2}$ respectivamente, pero la suma

${\displaystyle f(t)=\cos \left(t\right)+\cos \left(\sqrt{2}t\right)}$

no es periódica.

x=@(t) cos(2*pi*t)+cos(4*pi*t)/2;
subplot(2,1,1)
fplot(x,[0,10]);
xlabel('t')
ylabel('x')

subplot(2,1,2)
x=@(t) cos(2*pi*t)+cos(2*pi*sqrt(2)*t);
fplot(x,[0,10]);
xlabel('t')
ylabel('x')

Serie de Fourier

A primera vista, parece que el problema de analizar formas de ondas complejas representa una tarea formidable. Sin embargo, si la forma de la onda es periódica, se puede representar con una precisión arbitraria, mediante la superposición de un número suficientemente grande de ondas senoidales que forman una serie armónica.

Toda función f(t) periódica de periodo 2P, se puede representar en forma de una suma infinita de funciones armónicas, es decir,

${\displaystyle f(t)=\frac{a_0}{2}+{\displaystyle \sum _{k=1}^{\infty }\left(a_k\cos \frac{k\pi t}{P}+b_k\sin \frac{k\pi t}{P}\right)}}$

donde a₀ a₁ ...a_k ... y b₁ b₂ .... b_k .... son los denominados coeficientes de Fourier.

Teniendo en cuenta los resultados de las integrales

${\displaystyle {\displaystyle \underset{-P}{\overset{P}{\int }}\cos \frac{m\pi t}{P}}\sin \frac{n\pi t}{P}dt=\frac{P}{\pi }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\cos (mz)}\sin (nz)dz=0}$

>> syms t m n;
>> assume(n,'integer');
>> assume(m,'integer');
>> int('sin(m*t)*cos(n*t)',t,-pi,pi)
ans =0

${\displaystyle \begin{array}{l}{\displaystyle \underset{-P}{\overset{P}{\int }}\cos \frac{m\pi t}{P}}\cos \frac{n\pi t}{P}dt=\frac{P}{\pi }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\cos (mz)}\cos (nz)dt\\ \frac{P}{2\pi }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\left(\cos \left((m+n)z\right)+\cos \left((m-n)z\right)\right)}·dz=\{\begin{array}{l}0m\ne n\\ Pm=n\end{array}\end{array}}$

>> y=int('cos(m*t)*cos(n*t)',t,-pi,pi)
y=(2*(m*cos(pi*n)*sin(pi*m) - n*cos(pi*m)*sin(pi*n)))/(m^2 - n^2)
>> limit(y,m,n)
ans =pi*cos(pi*n)^2

Como n es entero, la respuesta es pi (π)

${\displaystyle \begin{array}{l}{\displaystyle \underset{-P}{\overset{P}{\int }}\sin \frac{m\pi t}{P}}\sin \frac{n\pi t}{P}dt=\frac{P}{\pi }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\sin (mz)}\sin (nz)dz\\ \frac{P}{2\pi }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\left(-\cos \left((m+n)z\right)+\cos \left((m-n)z\right)\right)}·dz=\{\begin{array}{l}0m\ne n\\ Pm=n\end{array}\end{array}}$

>> y=int('sin(m*t)*sin(n*t)',t,-pi,pi)
y =-(2*(m*cos(pi*m)*sin(pi*n) - n*cos(pi*n)*sin(pi*m)))/(m^2 - n^2)
>> limit(y,m,n)
ans =pi*cos(pi*n)^2

Los coeficientes del desarrollo en serie valen

${\displaystyle \begin{array}{l}{a}_k=\frac{1}{P}{\displaystyle \underset{-P}{\overset{P}{\int }}f(t)}\cos \frac{k\pi t}{P}dt\\ b_k=\frac{1}{P}{\displaystyle \underset{-P}{\overset{P}{\int }}f(t)}\sin \frac{k\pi t}{P}dt\end{array}}$

La suma parcial de las series de Fourier es

${\displaystyle s_n(t)=\frac{a_0}{2}+{\displaystyle \sum _{k=1}^n\left(a_k\cos \frac{k\pi t}{P}+b_k\sin \frac{k\pi t}{P}\right)}}$

Si la función f(t) tiene simetría, algunos de los coeficientes resultan nulos.

• Si f(t) es una función par, f(t)=f(-t), los términos b_k son nulos
• Si f(t) es impar f(t)=-f(-t), los coeficientes a_k son nulos

Función par

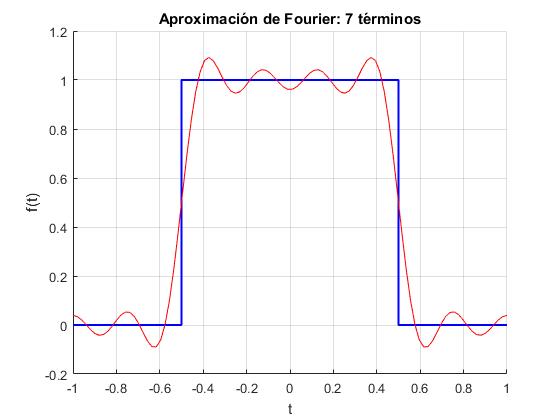
Por ejemplo, para el pulso rectangular simétrico de anchura 1, y periodo 2 se obtienen los siguientes coeficientes.

${\displaystyle \begin{array}{l}{a}_0=\frac{1}{1}{\displaystyle \underset{-0.5}{\overset{0.5}{\int }}dt}=1\\ a_k=\frac{1}{1}{\displaystyle \underset{-0.5}{\overset{0.5}{\int }}\cos \left(k\pi t\right)dt=}\frac{2}{k\pi }\left(\sin \left(\frac{k\pi }{2}\right)\right)\{\begin{array}{l}0k\text{par}\\ \frac{2}{k\pi }{\left(-1\right)}^{(k-1)/2}k\text{impar}\end{array}\end{array}}$

Vamos a reconstruir la función f(t) a partir del desarrollo en serie de Fourier.

${\displaystyle s_n(t)=\frac{1}{2}+\frac{2\cos (\pi t)}{\pi }-\frac{2\cos (3\pi t)}{3\pi }+\frac{2\cos (5\pi t)}{5\pi }-\frac{2\cos (7\pi t)}{7\pi }+\mathrm{...}}$

Elaboramos un script en el que

• Se establece el número n de términos del desarrollo en serie, sin contar el primero a₀/2.
• Se dibuja la función f(t) entre -1 y +1 en color azul y con ancho de línea 2.
• Se dibuja la aproximación a la función sumando n términos del desarrollo en serie en color rojo de anchura de línea 1.

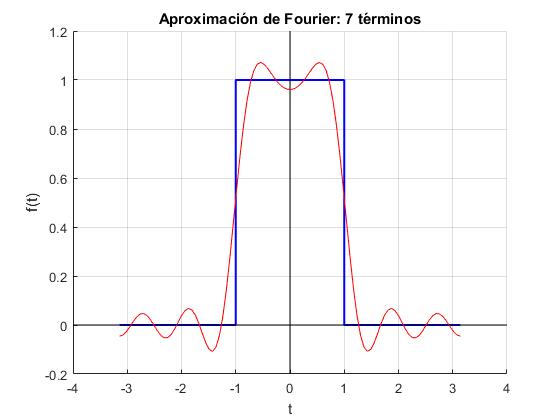
n=7;
hold on
x=[-1 -0.5 -0.5 0.5 0.5 1];
y=[0 0 1 1 0 0];
plot(x,y,'b','linewidth',1.5)
x=linspace(-1,1,100);
y=zeros(length(x),1);
for i=1:length(x)
    y(i)=1/2;
    for k=1:2:n
        y(i)=y(i)+(-1)^((k-1)/2)*2*cos(k*pi*x(i))/(k*pi);
     end
end
plot(x,y, 'r');
title(sprintf('Aproximación de Fourier: %i términos',n))
xlabel('t'); 
ylabel('f(t)')
grid on
hold off

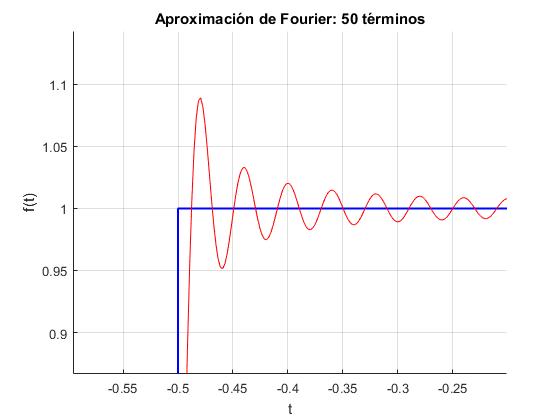
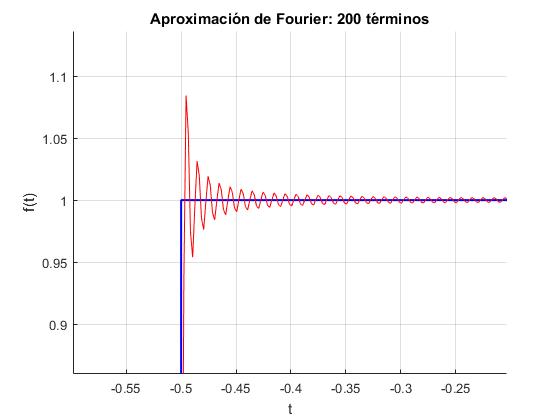
Aproximamos el pulso rectangular con 50 términos y con 200 términos. Cabría esperar que la serie convergiese a la función cuando se incrementa el número de términos, esto ocurre en casi todos los puntos excepto en las discontinuidades, cuando la función pasa de 0 a 1 en x=-0.5 y de 1 a 0 en x=0.5.

Se ha utilizado, las herramientas Zoom y Pan de la ventana gráfica para mostrar un trozo de la función próximo a x=-0.5

Función impar

Sea ahora la función

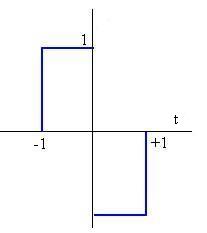
Es una función impar, los coeficientes a_k son nulos

${\displaystyle b_k={\displaystyle \underset{-1}{\overset{0}{\int }}\sin \left(k\pi t\right)dt}-{\displaystyle \underset{0}{\overset{1}{\int }}\sin \left(k\pi t\right)dt}=\frac{1}{k\pi }\left(-2+2\cos (k\pi )\right)=\{\begin{array}{l}0k\text{par}\\ \frac{-4}{k\pi }k\text{impar}\end{array}}$

El desarrollo en serie es

${\displaystyle s_n(t)=-\frac{4\sin (\pi t)}{\pi }-\frac{4\sin (3\pi t)}{3\pi }-\frac{4\sin (5\pi t)}{5\pi }-\frac{4\sin (7\pi t)}{7\pi }+\mathrm{...}}$

Escribimos un script en el que

• Se establece el número n de términos del desarrollo en serie.
• Se dibuja la función f(t) entre -1 y +1 en color azul y con ancho de línea 2.
• Se dibuja la aproximación a la función sumando n términos del desarrollo en serie en color rojo de anchura de línea 1.

n=7;
hold on
x=[-1 -1 0 0 1 1];
y=[0 1 1 -1 -1 0];
plot(x,y,'b','linewidth',1.5)
x=linspace(-1,1,100);
y=zeros(length(x),1);
for i=1:length(x)
    y(i)=0;
    for k=1:2:n
        y(i)=y(i)-4*sin(k*pi*x(i))/(k*pi);
     end
end
plot(x,y, 'r');
title(sprintf('Aproximación de Fourier: %i términos',n))
xlabel('t'); 
ylabel('f(t)')
grid on
hold off

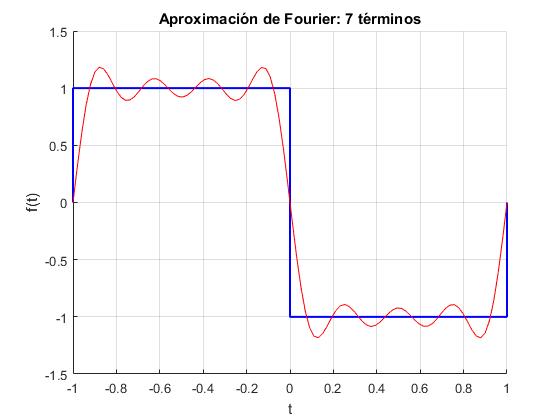
Desarrollo en serie de Fourier con MATLAB

La función heaviside de MATLAB

En MATLAB la función heaviside(t) se define del siguiente modo:

${\displaystyle u(t)=\{\begin{array}{l}0t<0\\ 0.5t=0\\ 1t>0\end{array}}$

Vamos a elaborar un script que nos permita obtener el desarrollo en serie de Fourier de una función f(t) periódica de periodo 2P.

Definimos primero, la función escalón

${\displaystyle f(t)=\{\begin{array}{l}0t<a\\ 1t\ge a\end{array}}$

Describimos la función escalón mediante la llamada a la función heaviside(t-a)

La función pulso rectangular del primer ejemplo,

${\displaystyle f(t)=\{\begin{array}{l}0t<-a\\ 1-a\le t\le a\\ 0t>a\end{array}}$

la definimos en MATLAB como heaviside(t+a)-heaviside(t-a), tal como vemos en la figura

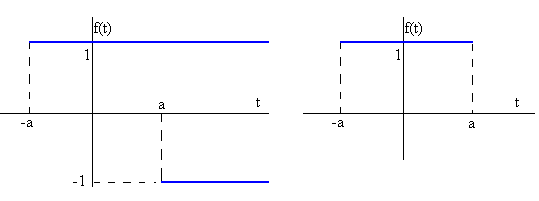
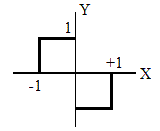
La función f(t).

${\displaystyle f(t)=\{\begin{array}{l}0t<-1\\ 1-1\le t<0\\ -10\le t<1\\ 0t\ge 1\end{array}}$

Se escribe en MATLAB como, (heaviside(t+1)-heaviside(t))+(-1)*(heaviside(t)-heaviside(t-1))= heaviside(t+1)-2*heaviside(t)+heaviside(t-1)

>> syms t;
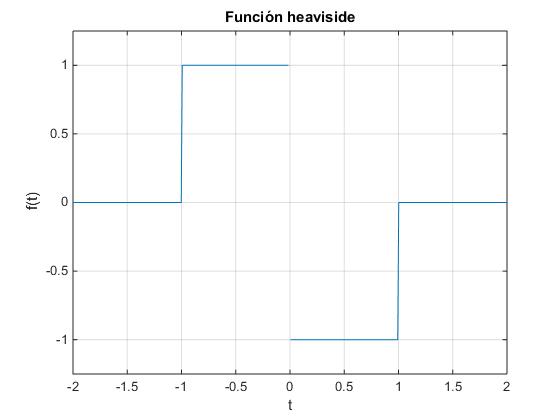
>> x=heaviside(t+1)-2*heaviside(t)+heaviside(t-1);
>> ezplot(x,[-2,2]);
>> xlabel('t'),
>> ylabel('f(t)')
>> title('Función heaviside')
>> grid on

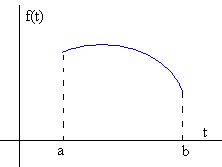
La función f(t) cualesquiera que toma valores distintos de cero en el intervalo [a,b] se escribe

${\displaystyle \left(u(t-a)-u(t-b)\right)f(t)=\{\begin{array}{l}0t<a\\ f(t)a\le t\le b\\ 0t>b\end{array}}$

Función par

Desarrollo en serie de Fourier de la primera función, el pulso rectangular

syms t;
P=1; %semiperiodo
f=heaviside(t+0.5)-heaviside(t-0.5);
a=@(k) int(f*cos(k*pi*t/P),t,-P,P)/P;
b=@(k) int(f*sin(k*pi*t/P),t,-P,P)/P;
fs=a(0)/2;
for k=1:10 %número de términos
    fs=fs+a(k)*cos(k*pi*t/P)+b(k)*sin(k*pi*t/P);
end
pretty(fs)

Otra forma alternativa, utilizando la función symsum de MATLAB

syms t k P n;
assume(k,'Integer')
a=@(f,t,k,P) int(f*cos(k*pi*t/P),x,-P,P)/P;
b=@(f,t,k,P) int(f*sin(k*pi*t/P),x,-P,P)/P;
fs=@(f,t,n,P) a(f,t,0,P)/2+symsum(a(f,t,k,P)*cos(k*pi*t/P)
+b(f,t,k,P)*sin(k*pi*t/P),k,1,n);
f=heaviside(t+0.5)-heaviside(t-0.5);
P=1; %semiperiodo
pretty(fs(f,t,10,P))

En la ventana de comandos vemos el desarrollo en serie de Fourier de esta función periódica para n=10 términos

2cos(pi t)   2cos(3pi t)   2cos(5pi t)   2cos(7pi t)   2cos(9pi t) 
--------- - ---------- + ------------- - ---------- + --------- + 1/2 
    pi        3pi           5pi            7pi            9pi

Función impar

Desarrollo en serie de Fourier de la segunda función

....
f=heaviside(t+1)-2*heaviside(t)+heaviside(t-1);
P=1; %semiperiodo
pretty(fs(f,x,10,P))

En la ventana de comandos vemos el desarrollo en serie de Fourier de esta función periódica para n=10 términos

4sin(pi t)   4sin(3pi t)   4sin(5pi t)   4sin(7pi t)   4 sin(9pi t) 
- -------- - ---------- - ------------- - ----------- - ------------- 
    pi            3 pi         5 pi        7 pi            9 pi

Ejemplo 1

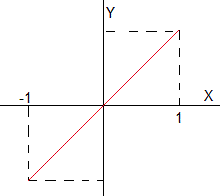
Sea la función periódica f(t)=t entre -1 y 1

Para estudiar otra función periódica basta cambiar la definición de la función f y el valor de su semiperiodo P. Cambiando el valor de N se muestran más o menos términos del desarrollo en serie.

syms t k P n;
assume(k,'Integer')
a = @(f,t,k,P) int(f*cos(k*pi*t/P),t,-P,P)/P;
b = @(f,t,k,P) int(f*sin(k*pi*t/P),t,-P,P)/P;
fs=@(f,t,n,P) a(f,t,0,P)/2+symsum(a(f,t,k,P)*cos(k*pi*t/P)
+b(f,t,k,P)*sin(k*pi*t/P),k,1,n);

%definición de la fuerza y su semiperiodo P
f=t;
P=1;

N=6; %términos del desarrollo en serie
pretty(fs(f,t,N,P))

hold on
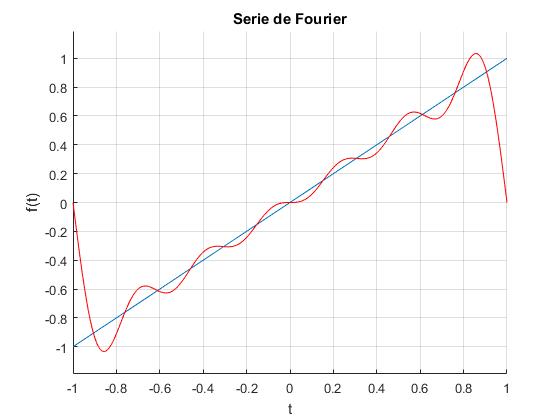
ezplot(f,[-P P])
hg=ezplot(fs(f,t,N,P),[-P P]);
set(hg,'color','r')
hold off
xlabel('t')
ylabel('f(t)')
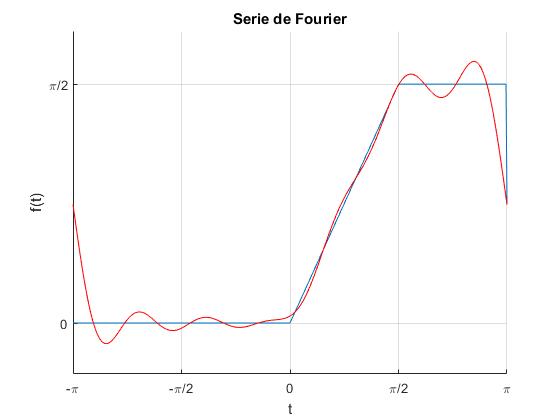
title('Serie de Fourier')

%armónicos
figure
k=1:N;
ak=a(f,t,k,P);
bk=b(f,t,k,P);
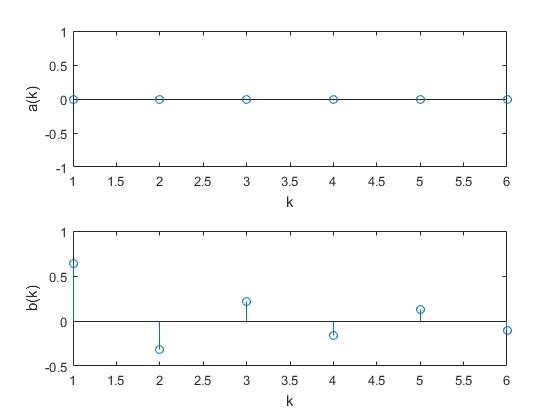
subplot(2,1,1)
stem(ak)
xlabel('k');
ylabel('a(k)')

subplot(2,1,2)
stem(bk)
xlabel('k');
ylabel('b(k)')

2sin(pi t)   sin(2pi t)   2 sin(3pi t)   sin(4pi t)  2sin(5pi t) sin(6pi t) 
----------- - ----------- + ---------- - -------- + ---------- - ----------- 
    pi           pi            3 pi         2 pi        5 pi        3 pi

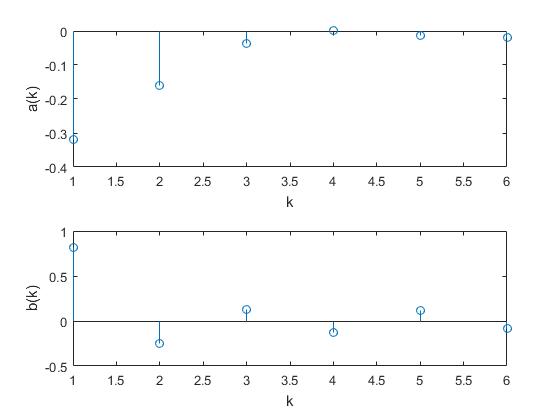
En la gráfica se representa la contribución de los N=6 primeros armónicos cada uno de los armónicos, en la parte superior los coeficientes a_k, y en la parte inferior los coeficientes b_k. Por ser f(t)=t una función impar, a_k=0,

Ejemplo 2

Sea la función

${\displaystyle f(t)=\{\begin{array}{l}0-\pi <t<0\\ t0\le t<\frac{\pi }{2}\\ \frac{\pi }{2}\frac{\pi }{2}\le t\le \pi \end{array}}$

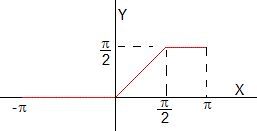
syms t k P n;
assume(k,'Integer')
a = @(f,t,k,P) int(f*cos(k*pi*t/P),t,-P,P)/P;
b = @(f,t,k,P) int(f*sin(k*pi*t/P),t,-P,P)/P;
fs=@(f,t,n,P) a(f,t,0,P)/2+symsum(a(f,t,k,P)*
cos(k*pi*t/P)+b(f,t,k,P)*sin(k*pi*t/P),k,1,n);

%definición de la fuerza y su semiperiodo P
f=t*(heaviside(t)-heaviside(t-pi/2))+
(heaviside(t-pi/2)-heaviside(t-pi))*pi/2;
P=pi;

N=6; %términos del desarrollo en serie
latex(fs(f,t,N,P))
hold on
ezplot(f,[-P P])
hg=ezplot(fs(f,t,N,P),[-P P]);
set(hg,'color','r')
set(gca,'XTick',-pi:pi/2:pi)
set(gca,'XTickLabel',{'-\pi','-\pi/2','0','\pi/2','\pi'})
set(gca,'YTick',0:pi/2:pi)
set(gca,'YTickLabel',{'0','\pi/2','\pi'})
hold off
grid on
xlabel('t')
ylabel('f(t)')
title('Serie de Fourier')

%armónicos
figure
k=1:N;
ak=a(f,t,k,P);
bk=b(f,t,k,P);
subplot(2,1,1)
stem(ak)
xlabel('k');
ylabel('a(k)')

subplot(2,1,2)
stem(bk)
xlabel('k');
ylabel('b(k)')

Utilizamos la función latex en combinación con el programa MathType para presentar los resultados del desarrollo en serie de Fourier

${\displaystyle \begin{array}{l}\frac{3\pi }{16}-\frac{\sin \text{}\left(2t\right)}{4}-\frac{\sin \text{}\left(4t\right)}{8}-\frac{\sin \text{}\left(6t\right)}{12}-\frac{\cos \text{}\left(2t\right)}{2\pi }-\frac{\cos \text{}\left(3t\right)}{9\pi }-\frac{\cos \text{}\left(5t\right)}{25\pi }\\ -\frac{\cos \text{}\left(6t\right)}{18\pi }-\frac{\cos \text{}\left(t\right)}{\pi }+\frac{\sin \text{}\left(t\right)\left(\frac{\pi }{2}+1\right)}{\pi }+\frac{\sin \text{}\left(3t\right)\left(\frac{3\pi }{2}-1\right)}{9\pi }+\frac{\sin \text{}\left(5t\right)\left(\frac{5\pi }{2}+1\right)}{25\pi }\end{array}}$

Ejemplo 3

Sea la función f(t)

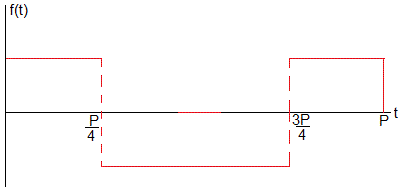
Expresamos la función f(t) en términos de la función heaviside de MATLAB

P=1;
f=@(t) heaviside(t)-2*heaviside(t-P/4)+2*heaviside(t-3*P/4)-heaviside(t-P);
fplot(f,[0,P])
grid on
ylim([-1.1,1.1])
xlabel('t')
ylabel('f(t)')
title('Función signo')

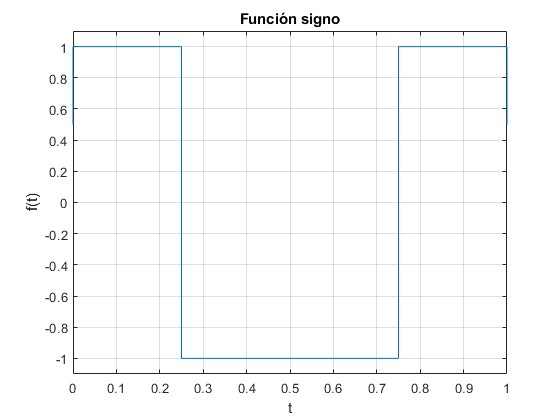
Se trata de una función simétrica, por lo que los términos b_k del desarrollo en serie son nulos

${\displaystyle \begin{array}{l}{a}_0=\frac{1}{P/2}{\displaystyle \underset{0}{\overset{P}{\int }}f(t)dt}=\frac{2}{P}\left\{\frac{P}{4}-\frac{P}{2}+\frac{P}{4}\right\}=0\\ a_k=\frac{1}{P/2}{\displaystyle \underset{0}{\overset{P}{\int }}f(t)\cos \frac{k\pi t}{P}dt}=\\ \frac{2}{P}\left\{{\displaystyle \underset{0}{\overset{P/4}{\int }}\cos \frac{k\pi t}{P}dt-{\displaystyle \underset{P/4}{\overset{3P/4}{\int }}\cos \frac{k\pi t}{P}dt+{\displaystyle \underset{3P/4}{\overset{P}{\int }}\cos \frac{k\pi t}{P}dt}}}\right\}=\frac{4}{k\pi }\left\{\sin \frac{k\pi }{4}-\sin \frac{3k\pi }{4}\right\}\end{array}}$

>> k=1:10;
>> sin(k*pi/4)-sin(3*k*pi/4)
ans =
   -0.0000    2.0000    0.0000   -0.0000    0.0000   -2.0000 
    0    0.0000   -0.0000    2.0000

Los coeficientes valen

${\displaystyle \begin{array}{l}{a}_1=\mathrm{0,}{a}_2=\frac{4}{\pi },a_3=\mathrm{0,}{a}_4=\mathrm{0,}{a}_5=\mathrm{0,}{a}_6=-\frac{4}{3\pi },a_7=\mathrm{0,}{a}_8=0\\ a_9=\mathrm{0,}{a}_{10}=\frac{4}{5\pi }\mathrm{,...}\end{array}}$

Aproximamos la función f(t) por el desarrollo en serie

${\displaystyle \begin{array}{l}f(t)=a_2\cos \left(\frac{2\pi t}{P}\right)+a_6\cos \left(\frac{6\pi t}{P}\right)+a_{10}\cos \left(\frac{10\pi t}{P}\right)+\mathrm{...}=\\ \frac{4}{\pi }\left\{\cos \left(\omega t\right)-\frac{1}{3}\cos \left(3\omega t\right)+\frac{1}{5}\cos \left(5\omega t\right)+\mathrm{...}\right\}\end{array}}$

con ω=2π/P. Comprobamos con Math Symbolic de MATLAB, tomando P=1

syms t;
P=1; %periodo
f=@(t) heaviside(t)-2*heaviside(t-P/4)+2*heaviside(t-3*P/4)-heaviside(t-P);
a=@(k) 2*int(f*cos(k*pi*t/P),t,0,P)/P;
fs=a(0)/2;
for k=1:20 %número de términos
    fs=fs+a(k)*cos(k*pi*t/P);
end
pretty(fs)
hold on
fplot(f,[0,P])
fplot(fs,[0,P])
hold off
grid on
xlabel('t')
ylabel('f(t)')
title('Aproximación')

cos(2 pi t) 4   cos(6 pi t) 4   cos(10 pi t) 4   cos(14 pi t) 4   cos(18 pi t) 4
------------- - ------------- + -------------- - -------------- + --------------
      pi             3 pi            5 pi             7 pi             9 pi

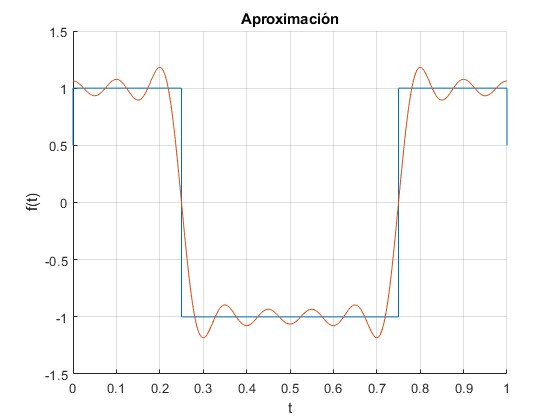
En la figura, hemos aproximado la función sgn(x) con los cinco primeros términos del desarrollo en serie de Fourier

${\displaystyle f(t)=\frac{4}{\pi }{\displaystyle \sum _{k,\text{impar}}^{\infty }\frac{{\left(-1\right)}^{(k-1)/2}}{k}\cos \left(k\omega t\right)}}$

Otra forma de aproximar la función f(t), conocidos los coeficientes a_k

function oscilador
    P=1; %semiperiodo
    f=@(t) heaviside(t)-2*heaviside(t-P/4)+2*heaviside(t-3*P/4)-heaviside(t-P);
    hold on
    fplot(f,[0,P])
    fplot(@(t) serie(t),[0,P])
    hold off
    grid on
    xlabel('t')
    ylabel('f(t)')
    title('Aproximación')

    function z=serie(t)
        z=0;
        for n=1:2:21
           z=z+(-1)^((n-1)/2)*cos(n*2*pi*t/P)/n;
        end
        z=z*4/pi;
    end
end

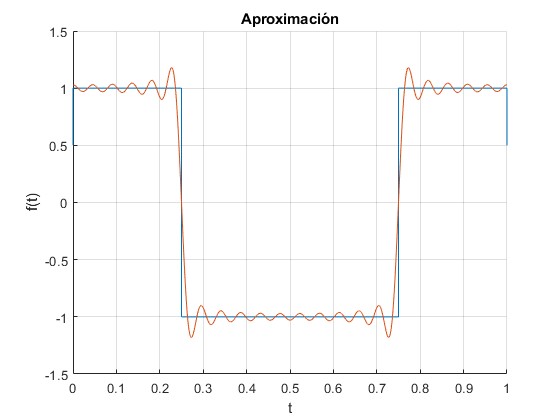
La forma compleja de las series de Fourier

Teniendo en cuenta las relaciones

${\displaystyle \begin{array}{l}{e}^{-i\omega t}=\cos \omega t-i\sin \omega t\\ e^{i\omega t}=\cos \omega t+i\sin \omega t\end{array}}$

El desarrollo en serie de Fourier

${\displaystyle f(t)=\frac{a_0}{2}+{\displaystyle \sum _{k=1}^{\infty }\left(a_k\cos \left(\frac{k\pi t}{P}\right)+b_k\sin \left(\frac{k\pi t}{P}\right)\right)}}$

se expresa de la siguiente forma alternativa

${\displaystyle \begin{array}{l}f(t)=\frac{a_0}{2}+{\displaystyle \sum _{k=1}^{\infty }\left(\frac{a_k}{2}\left(e^{ik\pi t/P}+e^{-ik\pi t/P}\right)+\frac{b_k}{2i}\left(e^{ik\pi t/P}-e^{-ik\pi t/P}\right)\right)}\\ c_0=\frac{a_0}{2}{c}_k=\frac{a_k-i{b}_k}{2}{c}_{-k}=\frac{a_k+i{b}_k}{2}\\ f(t)=c_0+{\displaystyle \sum _{k=1}^{\infty }\left(c_k{e}^{ik\pi t/P}+c_{-k}{e}^{-ik\pi t/P}\right)}\\ f(t)={\displaystyle \sum _{-\infty }^{\infty }{c}_k\exp \left(ik\pi \frac{t}{P}\right)}{c}_k=\frac{1}{2P}{\displaystyle \underset{-P}{\overset{P}{\int }}f(t)\exp \left(-ik\pi \frac{t}{P}\right)dt}\end{array}}$

donde P es el semiperiodo de la función periódica de periodo 2P

Pulso rectangular

${\displaystyle \begin{array}{l}P=\pi \\ c_k=\frac{1}{2\pi }{\displaystyle {\int }_{-a}^{a}A{e}^{-ikt}dt=}\frac{A}{k\pi }\sin \left(ka\right)=\{\begin{array}{l}k=0c_0=\frac{A}{\pi }a\\ k\ne 0c_k=\frac{A}{k\pi }\sin \left(ka\right)\end{array}\end{array}}$

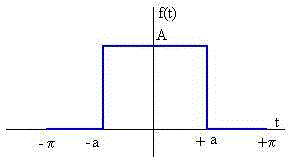
Escribimos un script en el que

• Se establece

• el número n de términos del desarrollo en serie.

• La semianchura a del pulso rectangular (menor que π)

• Se dibuja la función f(t) entre -π y +π en color azul y con ancho de línea 2.

• Se dibuja la aproximación a la función sumando n términos del desarrollo en serie (positivos y negativos) en color rojo de anchura de línea 1.

• Tomar A=1

a=1; %Semianchura del pulso rectangular a<pi
n=7; %número de terminos
hold on
x=[-pi -a -a a a pi];
y=[0 0 1 1 0 0];
plot(x,y,'b','linewidth',1.5)
x=linspace(-pi,pi,100);
y=zeros(length(x),1);

for j=1:length(x)
    y(j)=0;
    for k=-n:n
        if k==0 
            y(j)=y(j)+a/pi;
        else
            y(j)=y(j)+sin(k*a)*exp(1i*k*x(j))/(k*pi);
        end
     end
end
%ejes
plot([-4 4],[0 0],'k')
plot([0 0],[-0.2 1.2],'k')
%serie de Fourier
plot(x,real(y),'r');
title(sprintf('Aproximación de Fourier: %i términos',n))
xlabel('t'); 
ylabel('f(t)')
grid on
hold off

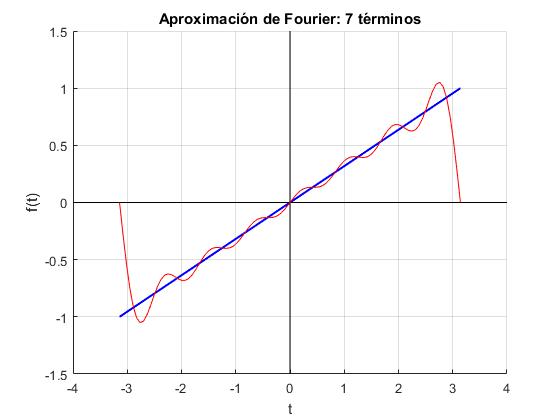
Pulso diente de sierra

${\displaystyle \begin{array}{l}P=\pi \\ c_k=\frac{1}{2\pi }{\displaystyle {\int }_{-\pi }^{\pi }\frac{A}{\pi }t{e}^{-ikt}dt=}\frac{A}{k\pi }i\cos \left(k\pi \right)=\frac{A}{k\pi }{\left(-1\right)}^{k}i\end{array}}$

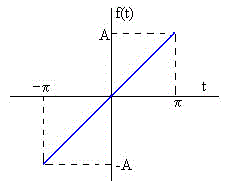
Escribir un script en el que

• Se establece

• el número n de términos del desarrollo en serie.

• Se dibuja la función f(t) entre -π y +π en color azul y con ancho de línea 2.

• Se dibuja la aproximación a la función sumando n términos del desarrollo en serie (positivos y negativos) en color rojo de anchura de línea 1.

• Tomar A=1

n=7; %Número de términos
hold on
plot([-pi,pi],[-1 1],'b','linewidth',1.5)
x=linspace(-pi,pi,100);
y=zeros(length(x),1);
for j=1:length(x)
    y(j)=0;
    for k=-n:n
        y(j)=y(j)+(-1)^k*1i*exp(1i*k*x(j))/(k*pi);
    end
end
%ejes
plot([-4 4],[0 0],'k')
plot([0 0],[-1.5 1.5],'k')
%serie de Fourier
plot(x,real(y), 'r');
title(sprintf('Aproximación de Fourier: %i términos',n))
grid on
xlabel('t'); 
ylabel('f(t)')
hold off