Hemos estudiado el oscilador más simple: un cuerpo de masa m unido a un muelle elástico de constante k. La frecuencia de las oscilaciones es

${\displaystyle {\omega }_0=\sqrt{\frac{k}{m}}}$

Vamos estudiar el comportamiento de un oscilador cuya masa m va disminuyendo con el tiempo t, a medida que sale agua del depósito. Observaremos como la frecuencia aumenta con el tiempo hasta que se vacía el depósito. A partir de ese momento, la frecuencia se mantiene constante e igual a

${\displaystyle {\omega }_0=\sqrt{\frac{k}{M}}}$

siendo M la masa del depósito vacío

Vaciado del depósito

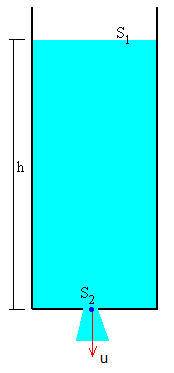
En la página "Vaciado de un depósito abierto", hemos aplicado la ecuación de continuidad y la ecuación de Bernoulli, para obtener la variación de la altura h del depósito con el tiempo t.

La velocidad u de salida del agua vale

${\displaystyle u=S_1\sqrt{\frac{2gh}{S_1^2-S_2^2}}=f\sqrt{\frac{2gh}{f^2-1}}f=\frac{S_1}{S_2}}$

El volumen de fluido que sale del depósito en la unidad de tiempo es S₂u y en el tiempo dt será S₂u·dt. Como consecuencia disminuirá la altura h de agua en el depósito

${\displaystyle \begin{array}{l}-S_{1}dh=S_{2}u·dt\\ \frac{dh}{dt}=-\frac{u}{f}\\ dh=-\sqrt{\frac{2gh}{f^2-1}}dt\end{array}}$

Sabiendo que en el instante t=0, la altura inicial de agua en el depósito es H. Integramos para obtener la altura h de agua en el depósito en el instante t.

${\displaystyle \begin{array}{l}{\displaystyle \underset{H}{\overset{h}{\int }}\frac{dh}{\sqrt{h}}}=\sqrt{\frac{2g}{f^2-1}}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ \sqrt{H}-\sqrt{h}=\left(\sqrt{\frac{g}{2\left(f^2-1\right)}}\right)t\end{array}}$

El depósito se vacía, h=0 en el instante t_max

${\displaystyle t_{\max }=\sqrt{\frac{2H\left(f^2-1\right)}{g}}}$

Centro de masa del sistema formado por el depósito y el agua.

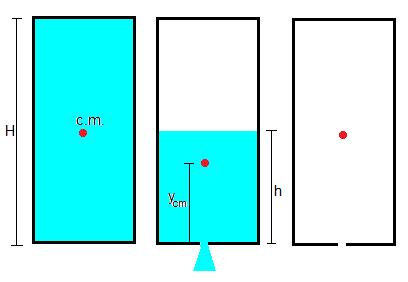
Sea un recipiente vacío de forma cilíndrica de masa M, sección S₁=A y altura H, abierto por la parte superior para que entre aire a medida que se sale agua por el orificio situado en su base. Supongamos que su centro de masas está situado a una altura H/2 de la base. Cuando se llena de agua, el centro de masas no cambia, tal como se aprecia en la figura de la izquierda.

Cuando el agua en el depósito tiene una altura h, la posición del centro de masas habrá cambiado. La masa de agua que hay en el depósito es m=ρAH. Donde ρ=1000 kg/m³ es la densidad del agua. Cuando el depósito se ha vaciado completamente, el centro de masas volverá al valor inicial H/2, tal como se ve en las figuras.

La altura del centro de masas, medido desde la base, en función de h es

${\displaystyle y_{cm}=\frac{M\left(H/2\right)+\rho Ah\left(h/2\right)}{M+\rho Ah}}$

La altura y_cm del centro de masa cambia con el tiempo t a medida que sale agua por el orificio.

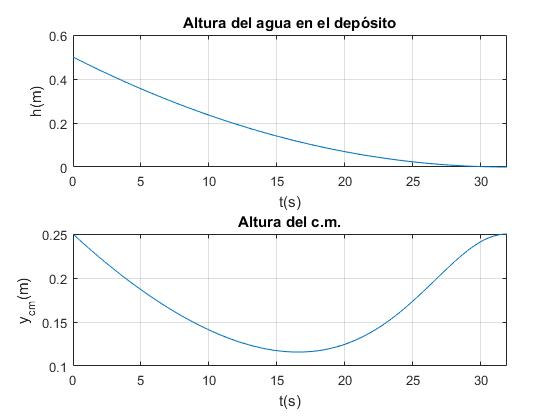
H=0.5;   %altura del depósito
M=1.0; %masa del cubo vacío
rho=1000; %densidad del agua
A=0.02; % 10 litros en un cilindro de 0.05 m de altura
f=1/0.01; %cociente S1/S2 (sección cilindro/área orificio)
tMax=sqrt(2*H*(f^2-1)/9.8);
h= @(t) (sqrt(H)-sqrt(4.9/(f^2-1))*t)^2;

subplot(2,1,1)
fplot(h,[0,tMax])
grid on
xlabel('t(s)')
ylabel('h(m)')
title('Altura del agua en el depósito')

subplot(2,1,2)
y_cm=@(t) (M*(H/2)+rho*A*h(t)^2/2)/(M+rho*A*h(t));
fplot(y_cm,[0,tMax])
grid on
xlabel('t(s)')
ylabel('y_c_m(m)')
title('Altura del c.m.')

Ecuación del movimiento

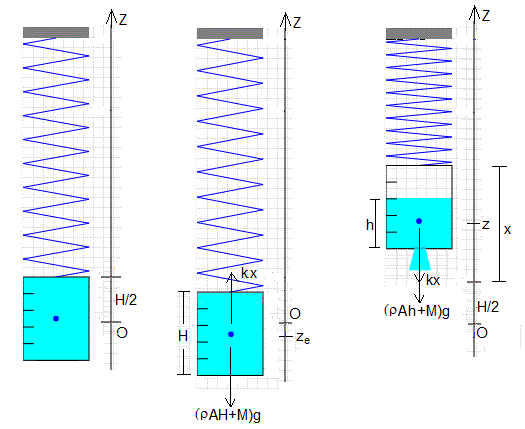
Posición inicial de equilibrio

Situamos el origen en el centro de masas del depósito lleno cuando lo atamos a un muelle inicialmente no deformado. Denominaremos z a la posición del centro de masas que ya no coincidirá con el centro del depósito cuando empiece a vaciarse. El eje Z apunta hacia arriba

En la situación de equilibrio, la posición del c.m es z_e por debajo del origen. El muelle se deforma x=-z_e. Las fuerzas que actúan sobre el c.m. del depósito son:

• el peso (ρAh+M)g, la masa de agua más la masa M del depósito vacío
• la fuerza que ejerce el muelle kx

En el equilibrio

${\displaystyle \begin{array}{l}x=\frac{(M+\rho AH)g}{k}\\ z_e=-x\end{array}}$

El depósito lleno de agua se desvía de la posición de equilibrio, se suelta a la vez que el agua empieza a salir por el orificio situado en su base inferior. Vamos a estudiar el movimiento del centro de masas del sistema formado por el depósito y el agua que permenece en su interior.

Hemos formulado las ecuaciones de un sistema de masa variable en varias páginas, una de ellas, es el movimiento vertical de un cohete,

${\displaystyle m\frac{dv}{dt}+u\frac{dm}{dt}=F_{ext}}$

Donde m es la masa total del cohete, u es la velocidad de escape de los gases relativa al cohete y dm/dt la variación de su masa con el tiempo, F_ext es la resultante de las fuerzas (el peso) que se aplican en el centro de masas.

En el sistema que se estudia en esta página, las fuerzas que se ejercen sobre el centro del masas del depósito lleno de agua hasta una altura h son: el peso (M+ρAh)g y la fuerza que ejerce el muelle elástico deformado kx.

Sea z la posición del c.m. La ecuación del movimiento del centro de masas es

${\displaystyle \left(\rho Ah+M\right)\frac{d^{2}z}{d{t}^2}+u\frac{d\left(\rho Ah\right)}{dt}=-kx-\left(\rho Ah+M\right)g}$

siendo x la deformación del muelle, que relacionamos con la posición z del centro de masas del depósito lleno de agua hasta una altura h.

${\displaystyle \begin{array}{l}x+\frac{H}{2}=z-y_{cm}+H\\ x=z-y_{cm}+\frac{H}{2}\end{array}}$

Hemos calculado en apartados anteriores, la variación de la altura h de agua en el depósito en función del tiempo t, la velocidad u de salida de agua por el orificio practicado en el fondo del recipiente y la altura y_cm del centro de masas.

${\displaystyle \begin{array}{l}\left(\rho Ah+M\right)\frac{d^{2}z}{d{t}^2}=f\rho A\frac{2gh}{f^2-1}-k\left(z-y_{cm}+\frac{H}{2}\right)-\left(\rho Ah+M\right)g\\ \sqrt{h}=\sqrt{H}-\left(\sqrt{\frac{g}{2\left(f^2-1\right)}}\right)t\\ y_{cm}=\frac{M\left(H/2\right)+\rho Ah\left(h/2\right)}{M+\rho Ah}\end{array}}$

Se resuelve la ecuación diferencial, con las condiciones iniciales siguientes: en el instante t=0, z=z₀, dz/dt=0.

Una vez calculada la posición z del c.m. del sistema formado por el depósito y el agua que permanece en el depósito, determinamos la posición del centro del depósito mediante la transformación z-y_cm+H/2 tal como puede verse en las figuras (más arriba)

H=0.5;   %altura del depósito
M=1.0; %masa del cubo vacío
rho=1000; %densidad del agua
A=0.02; % 10 litros en un cilindro de 0.05 m de altura
f=1/0.01; %cociente S1/S2 (sección cilindro/área orificio)
ks=100;
tMax=sqrt(2*H*(f^2-1)/9.8);
 
%condiciones iniciales
x0=[-(M+rho*A*H)*9.8/ks,0];
%x0=[0,0];

tspan=[0 tMax];
p=[f, A, H, M, ks, rho, tMax];
[t,x]=ode45(@muelle_cubo_ode,tspan,x0,[],p);
h= @(t) (sqrt(H)-sqrt(4.9/(f^2-1))*t).^2;
xDeposito=x(:,1)-(M*H/2+rho*A*h(t).^2/2)./(M+rho*A*h(t))+H/2; %centro del depósito
plot(t,xDeposito)
grid on
xlabel('t(s)')
ylabel('x')
title('Oscilador de masa variable')

function ret =muelle_cubo_ode(t,x,p)
    f=p(1);
    A=p(2);
    H=p(3);
    M=p(4);
    ks=p(5);
    rho=p(6);
    tMax=p(7);
    
    h=0;
    if t<tMax  %mientras el depósito tenga agua
        h=(sqrt(H)-sqrt(4.9/(f*f-1))*t)^2;
    end
    deforma=x(1)-(M*H/2+rho*A*h*h/2)/(M+rho*A*h)+H/2;
    ret=[x(2);(f*rho*A*2*9.8*h/(f*f-1)-ks*deforma)/(M+rho*A*h)-9.8];
end

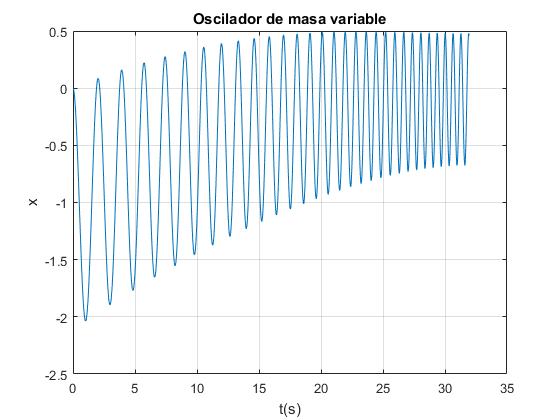
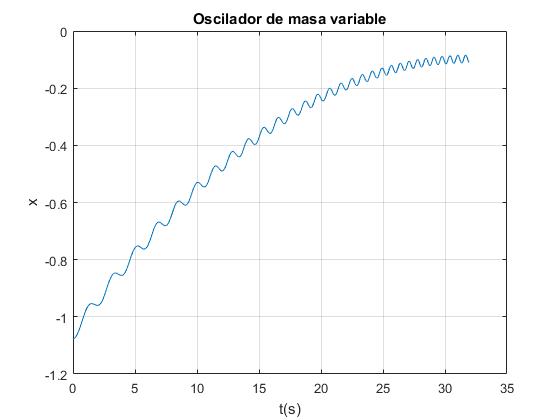
Un caso especialmente importante es aquél en el que la posición inicial del c.m. es la posición de equilibrio y se abre la llave que permite la salida de agua del depósito, vemos que el centro del depósito parte de la posición de equilibrio con el depósito lleno

${\displaystyle z_e=-\frac{(M+\rho AH)g}{k}}$

y llega a la posición final de equilibrio con el depósito vacío, realizando pequeñas oscilaciones en torno a las sucesivas posiciones de equilibrio

${\displaystyle z_e=-\frac{Mg}{k}}$

Actividades

Se introduce

• La constante elástica del muelle k en el control de edición titulado Constante
• El parámetro f, cociente entre las áreas de las secciones del depósito y del orificio que determina el tiempo de vaciado del agua del depósito, en el control titulado sección/orificio
• La posición inicial del centro del depósito en el momento en el que se abre el orificio inferior y se empieza a contar el tiempo, en el control titulado Posición

El programa interactivo ha fijado los siguientes valores de los parámetros

• Masa del depósito, M=1 kg
• La masa de agua en el depósito de 10 litros es 10 kg, ya que la densidad del agua es ρ=1000 kg/m³
• Altura de agua en el depósito, H=0.5 m, por lo que la la sección del depósito es, A=0.02 m²

Se pulsa el botón titulado Nuevo

Ejemplo

Sea la constante del muelle k=100 N/m y el parámetro f=100

La posición de equilibrio del depósito lleno cuando se cuelga del muelle es

${\displaystyle z_e=-\frac{(M+\rho AH)g}{k}=-\frac{(1+1000·0.02·0.5)9.8}{100}=-1.078}$

Cuando el depósito se vacía completamente, la posición de equilibrio es

${\displaystyle z_e=-\frac{Mg}{k}=-\frac{1·9.8}{100}=-0.098}$

Referencias

Hilário Rodrigues, Nelson Panza, Dirceu Portes, Alexandre Soares. The motion of a leaking oscillator: a study for the physics class. Physics Education, 49 (5) September 2014, pp. 557-563