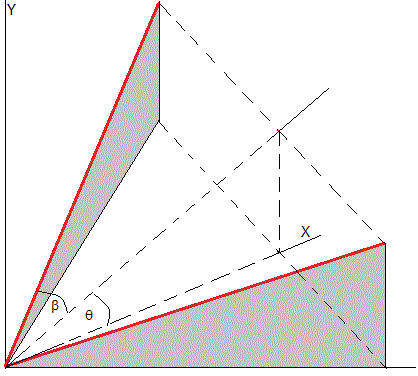
Los dos raíles están situados en un plano que forma un ángulo θ con el plano horiozontal. No son paralelos sino que se cortan en el origen formando un ángulo 2β

Para determinar la posición del centro de masas del doble cono, se estable en sistema de referencia XY en el plano vertical, bisetriz de las dos raíles.

El doble cono, está formado por dos conos iguales unidos por sus bases. Tiene un radio R en la base y forma un ángulo α con el eje. Cuando se apoya en los dos raíles, la distancia entre el eje y el punto de contacto es r tal como se muestra en la figura más abajo.

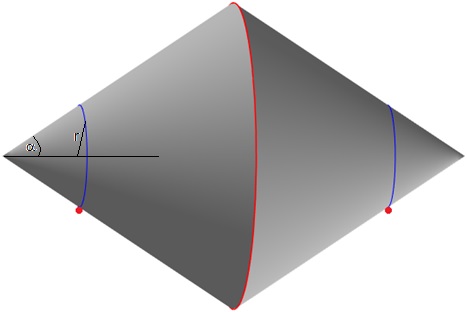
El código para representar el doble cono es

theta=pi/3;
r=linspace(0,1,30);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi)*sin(theta);
y=r.*sin(phi)*sin(theta);
z=r*cos(theta);
hold on
surfl(x,y,z);
surfl(x,y,cos(theta)+fliplr(z));
fplot3(@(t) sin(theta)*cos(t), @(t) sin(theta)*sin(t), @(t) cos(theta),
[0,2*pi], 'lineWidth', 1.2, 'color','r')
fplot3(@(t) sin(theta)*cos(t)/3, @(t) sin(theta)*sin(t)/3, @(t) cos(theta)/3,
[0,2*pi], 'color','b')
fplot3(@(t) sin(theta)*cos(t)/3, @(t) sin(theta)*sin(t)/3, @(t) 5*cos(theta)/3,
[0,2*pi], 'color','b')
hold off
shading interp
colormap(gray);
axis off
view (0,17)

Posición del centro de masas

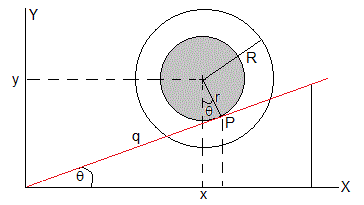
La proyección del doble cono sobre el plano bisetriz XY se muestra en la figura

Sabiendo que q es la distancia del punto P al origen. La posición del centro de masas del doble cono es

${\displaystyle \{\begin{array}{l}x=q\cos \theta -r\sin \theta \\ y=q\sin \theta +r\cos \theta \end{array}}$

La relación entre q y r se establece en la siguiente figura

${\displaystyle \begin{array}{l}\{\begin{array}{l}R-r=z\tan \alpha \\ z=q\tan \beta \end{array}\\ R-r=q\tan \beta ·\tan \alpha \end{array}}$

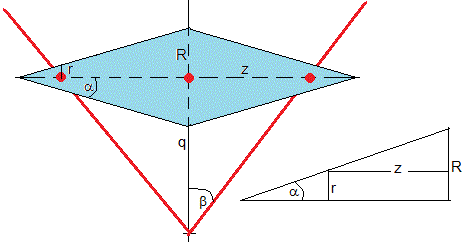
La relación entre las coordenadas x e y del centro de masas es la siguiente

${\displaystyle \begin{array}{l}\{\begin{array}{l}x=q\cos \theta -\left(R-q\tan \beta ·\tan \alpha \right)\sin \theta \\ y=q\sin \theta +\left(R-q\tan \beta ·\tan \alpha \right)\cos \theta \end{array}\\ \{\begin{array}{l}x+R\sin \theta =q\left(\cos \theta +\tan \beta ·\tan \alpha \sin \theta \right)\\ y-R\cos \theta =q\left(\sin \theta -\tan \beta ·\tan \alpha \cos \theta \right)\end{array}\\ \frac{y-R\cos \theta }{x+R\sin \theta }=\frac{\sin \theta -\tan \beta ·\tan \alpha \cos \theta }{\cos \theta +\tan \beta ·\tan \alpha \sin \theta }\\ \frac{y-R\cos \theta }{x+R\sin \theta }=\frac{\tan \theta -\tan \beta ·\tan \alpha }{1+\tan \beta ·\tan \alpha \tan \theta }\\ y=\frac{\tan \theta -\tan \beta ·\tan \alpha }{1+\tan \beta ·\tan \alpha \tan \theta }x+R\cos \theta +\frac{\tan \theta -\tan \beta ·\tan \alpha }{1+\tan \beta ·\tan \alpha \tan \theta }R\sin \theta \\ y=\frac{\tan \theta -\tan \beta ·\tan \alpha }{1+\tan \beta ·\tan \alpha \tan \theta }x+\frac{R}{\cos \theta \left(1+\tan \beta ·\tan \alpha \tan \theta \right)}\end{array}}$

Se trata de la ecuación de una recta de pendiente

${\displaystyle m=\frac{\tan \theta -\tan \beta ·\tan \alpha }{1+\tan \beta ·\tan \alpha \tan \theta }}$

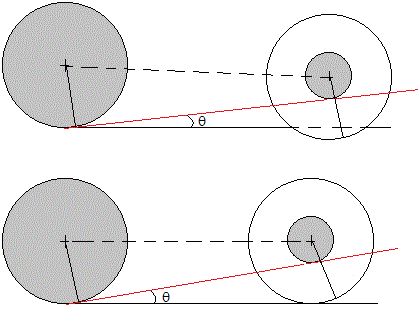
Consideraremos dos casos

• La pendiente es negativa m<0, cuando $\tan \theta <\tan \beta ·\tan \alpha$

• La pendiente es nula m=0, cuando $\tan \theta =\tan \beta ·\tan \alpha$

Denominaremos

${\displaystyle k=\tan \alpha ·\tan \beta }$

La relación entre q y r se escribe

${\displaystyle r=R-kq}$

Si el doble cono rueda sin deslizar, existe una relación entre el desplazamiento lineal, dq y el angulo girado, dφ

${\displaystyle \begin{array}{l}dq=rd\phi \\ dq=\left(R-kq\right)d\phi \\ \frac{dq}{R-kq}=d\phi \end{array}}$

Integramos con las siguientes condiciones q=0, para φ=0

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{q}{\int }}\frac{dq}{R-kq}}={\displaystyle \underset{0}{\overset{\phi }{\int }}d\phi }\\ -\frac{1}{k}\left\{\ln \left(R-kq\right)-\ln R\right\}=\phi \\ q=\frac{R}{k}\left(1-e^{-k\phi }\right)\\ r=R-kq=R{e}^{-k\phi }\end{array}}$

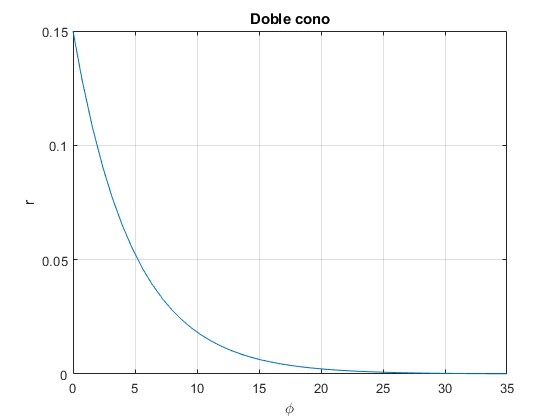
Cuando el ángulo girado φ se hace grande q→R/k, r→0

Representamos q en función del ángulo girado φ para

• Angulo del doble cono, α=30°
• Radio de la base del cono, R=0.15 m
• Angulo mitad entre los raíles, β=20°

alfa=pi/6;
beta=20*pi/180;
R=0.15;
k=tan(alfa)*tan(beta);
fplot(@(x) R*(1-exp(-k*x))/k,[0,35])
line([0,35],[R/k,R/k],'lineStyle','--')
grid on
ylim([0,0.8])
xlabel('\phi')
ylabel('q');
title('Doble cono')

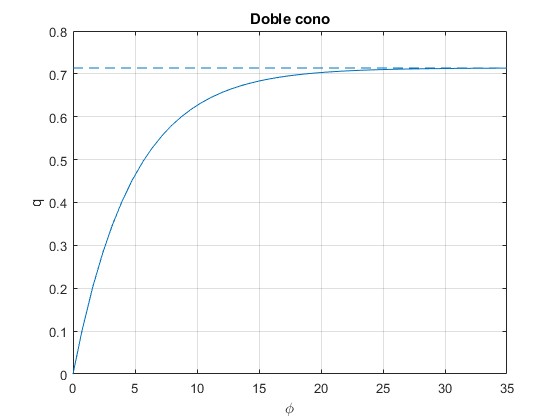
Representamos r en función del ángulo girado φ para los mismos datos

alfa=pi/6;
beta=20*pi/180;
R=0.15;
k=tan(alfa)*tan(beta);
fplot(@(x) R*exp(-k*x),[0,35])
grid on
xlabel('\phi')
ylabel('r');
title('Doble cono')

Expresamos la posición del centro de masas del cono (x,y) en términos del ángulo girado φ

${\displaystyle \begin{array}{l}\{\begin{array}{l}x=\frac{R\cos \theta }{k}\left(1-e^{-k\phi }\right)-R\sin \theta ·e^{-k\phi }\\ y=\frac{R\sin \theta }{k}\left(1-e^{-k\phi }\right)+R\cos \theta ·e^{-k\phi }\end{array}\\ \{\begin{array}{l}x=\frac{R\cos \theta }{k}-R\left(\frac{\cos \theta }{k}+\sin \theta \right)e^{-k\phi }\\ y=\frac{R\sin \theta }{k}+R\left(\cos \theta -\frac{\sin \theta }{k}\right)e^{-k\phi }\end{array}\end{array}}$

Conservación de la energía

La energía cinética del doble cono es la suma de la energía cinética de traslación del centro de masas y la de rotación alrededor del eje que pasa por el centro de masas. El momento de inercia del doble cono respecto del eje que pasa por los vértices es I=3MR²/10

${\displaystyle E_k=\frac{1}{2}M\left({\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2\right)+\frac{1}{2}\left(\frac{3}{10}M{R}^2\right){\left(\frac{d\phi }{dt}\right)}^2}$

Las componentes de la velocidad del centro de masas son

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{dx}{dt}=R\left(\cos \theta +k\sin \theta \right)e^{-k\phi }\frac{d\phi }{dt}\\ \frac{dy}{dt}=-R\left(k\cos \theta -\sin \theta \right)e^{-k\phi }\frac{d\phi }{dt}\end{array}\\ {\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2=R^2\left(1+k^2\right)e^{-2k\phi }{\left(\frac{d\phi }{dt}\right)}^2\end{array}}$

La energía cinética es

${\displaystyle E_k=\frac{1}{2}M{R}^2\left\{\left(1+k^2\right)e^{-2k\phi }+\frac{3}{10}\right\}{\left(\frac{d\phi }{dt}\right)}^2}$

La energía potencial

${\displaystyle E_p=Mgy=MgR\left(\frac{\sin \theta }{k}+\left(\cos \theta -\frac{\sin \theta }{k}\right)e^{-k\phi }\right)}$

La energía es constante e igual a la inicial E₀

${\displaystyle E=\frac{1}{2}M{R}^2\left\{\left(1+k^2\right)e^{-2k\phi }+\frac{3}{10}\right\}{\left(\frac{d\phi }{dt}\right)}^2+MgR\left(\frac{\sin \theta }{k}+\left(\cos \theta -\frac{\sin \theta }{k}\right)e^{-k\phi }\right)}$

Ecuación del movimiento

La Lagrangiana es

${\displaystyle L=\frac{1}{2}M{R}^2\left\{\left(1+k^2\right)e^{-2k\phi }+\frac{3}{10}\right\}{\left(\frac{d\phi }{dt}\right)}^2-MgR\left(\cos \theta -\frac{\sin \theta }{k}\right)e^{-k\phi }-MgR\frac{\sin \theta }{k}}$

La ecuación del movimiento

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\phi }}\right)-\frac{\partial L}{\partial \phi }=0\\ \frac{d}{dt}\left(M{R}^2\left\{\left(1+k^2\right)e^{-2k\phi }+\frac{3}{10}\right\}\frac{d\phi }{dt}\right)-\frac{1}{2}M{R}^2\left(1+k^2\right)\left(-2k\right)e^{-2k\phi }{\left(\frac{d\phi }{dt}\right)}^2+MgR\left(\cos \theta -\frac{\sin \theta }{k}\right)\left(-k\right)e^{-k\phi }=0\\ M{R}^2\left(1+k^2\right)\left(-2k\right)e^{-2k\phi }{\left(\frac{d\phi }{dt}\right)}^2+M{R}^2\left\{\left(1+k^2\right)e^{-2k\phi }+\frac{3}{10}\right\}\frac{d^2\phi }{d{t}^2}+M{R}^2\left(1+k^2\right)k{e}^{-2k\phi }{\left(\frac{d\phi }{dt}\right)}^2-MgR\left(\cos \theta -\frac{\sin \theta }{k}\right)k{e}^{-k\phi }=0\\ R\left\{\left(1+k^2\right)e^{-2k\phi }+\frac{3}{10}\right\}\frac{d^2\phi }{d{t}^2}-R\left(1+k^2\right)k{e}^{-2k\phi }{\left(\frac{d\phi }{dt}\right)}^2-g\left(k\cos \theta -\sin \theta \right)k{e}^{-k\phi }=0\end{array}}$

Pendiente nula, m=0

La pendiente es nula m=0, cuando $\tan \theta =\tan \beta ·\tan \alpha$, o bien, tanθ=k

Representamos la distancia q al origen en función del tiempo, con las condiciones iniciales siguientes, para t=0, q=0 y dq/dt=0.3 m/s. Se lanza desde el origen con una velocidad inicial

Teniendo en cuenta la relación entre la distancia q y el ángulo girado φ

${\displaystyle \begin{array}{l}q=\frac{R}{k}\left(1-e^{-k\phi }\right)\\ \frac{dq}{dt}=R{e}^{-k\phi }\frac{d\phi }{dt}\end{array}}$

Para q₀=0, φ₀=0. Para (dq/dt)₀=0.3, (dφ/dt)₀=0.3/R. Los datos son

• Angulo del doble cono, α=30°
• Radio de la base del cono, R=0.15 m
• Angulo mitad entre los raíles, β=20°
• Inclinación, θ=arctank

 alfa=pi/6;
beta=20*pi/180;
R=0.15; %radio
k=tan(beta)*tan(alfa);
theta=atan(k);
f=@(t,x) [x(2); ((9.8/R)*(k*cos(theta)-sin(theta))*exp(-k*x(1))+
(1+k^2)*k*exp(-2*k*x(1))*x(2)^2)/((1+k^2)*exp(-2*k*x(1))+3/10)];
[t,x]=ode45(f,[0,8],[0,0.3/R]);
q=R*(1-exp(-k*x(:,1)))/k;
plot(t,q)
grid on
xlabel('t')
ylabel('q');
title('Doble cono')
E0=R^2*(13/10+k^2)*(0.3/R)^2/2+9.8*R*cos(theta);
E=R^2*((1+k^2)*exp(-2*k*x(:,1))+3/10).*x(:,2).^2/2+9.8*R*(sin(theta)/k+
(cos(theta)-sin(theta)/k)*exp(-k*x(:,1)));
disp(E0)
disp(E)

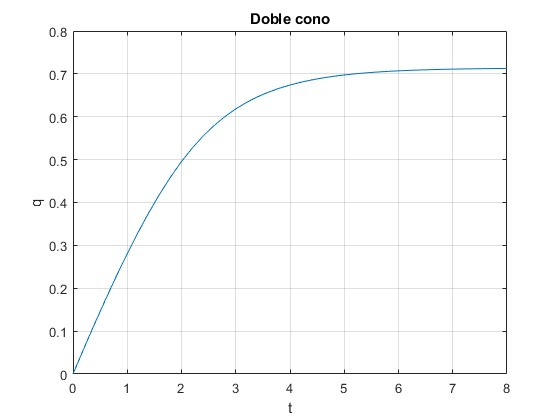
Comprobamos que la energía E se mantiene constante e igual a la inicial E₀

    1.4991

    1.4991
    1.4991
    ....
    1.4991

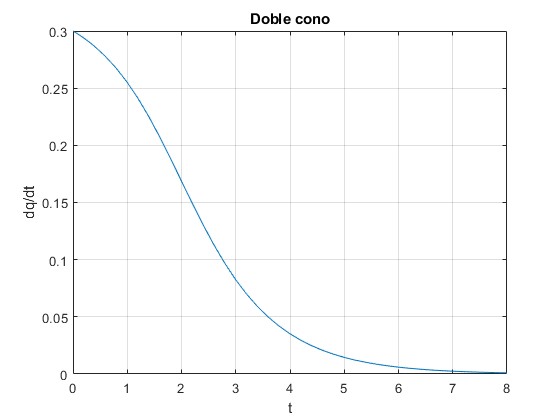
Representamos la velocidad dq/dt en función del tiempo t

alfa=pi/6;
beta=20*pi/180;
R=0.15; %radio
k=tan(beta)*tan(alfa);
theta=atan(k);
f=@(t,x) [x(2); ((9.8/R)*(k*cos(theta)-sin(theta))*exp(-k*x(1))+
(1+k^2)*k*exp(-2*k*x(1))*x(2)^2)/((1+k^2)*exp(-2*k*x(1))+3/10)];
[t,x]=ode45(f,[0,8],[0,0.3/R]);
dq=R*exp(-k*x(:,1)).*x(:,2);
plot(t,dq)
grid on
xlabel('t')
ylabel('dq/dt');
title('Doble cono')

Representamos en color rojo, la sucesión de puntos de contacto de un cono con el raíl

La distancia r del punto de contacto al eje del cono es

${\displaystyle r=R{e}^{-k\phi }}$

La distancia z a lo largo del eje del cono (desde la base) es

${\displaystyle z=q\tan \beta =\frac{R}{k}\left(1-e^{-k\phi }\right)\tan \beta }$

alfa=pi/6;
beta=20*pi/180;
R=0.15; %radio
k=tan(beta)*tan(alfa);
theta=atan(k);
f=@(t,x) [x(2); ((9.8/R)*(k*cos(theta)-sin(theta))*exp(-k*x(1))+
(1+k^2)*k*exp(-2*k*x(1))*x(2)^2)/((1+k^2)*exp(-2*k*x(1))+3/10)];
[t,x]=ode45(f,[0,8],[0,0.3/R]);
r=R*exp(-k*x(:,1));
q=R*(1-exp(-k*x(:,1)))/k;
z=q*tan(beta);
%cono
rr=linspace(0,R/sin(alfa),30);
xi=linspace(0,2*pi,30);
[rr,xi]=meshgrid(rr,xi);
X=rr.*cos(xi)*sin(alfa);
Y=rr.*sin(xi)*sin(alfa);
Z=rr*cos(alfa);
hold on
surfl(X,Z,Y);
plot3(r.*cos(x(:,1)), R/tan(alfa)-z, r.*sin(x(:,1)), 'lineWidth',1.2,'color','r')
hold off
shading interp
colormap(gray);
axis off
view (-123,1)

Pendiente negativa, m<0

La pendiente es negativa m<0, cuando $\tan \theta <\tan \beta ·\tan \alpha$, o bien, tanθ<k

Representamos la distancia q al origen en función del tiempo, con las condiciones iniciales siguientes, para t=0, q=0.99R/k y dq/dt=-0.022 m/s. Se lanza desde lejos hacia el origen y luego, regresa

Teniendo en cuenta la relación entre la distancia q y el ángulo girado φ

${\displaystyle \begin{array}{l}q=\frac{R}{k}\left(1-e^{-k\phi }\right)\\ \frac{dq}{dt}=R{e}^{-k\phi }\frac{d\phi }{dt}\end{array}}$

Para q₀=0.99R/k, φ₀=-ln(0.01)/k. Para (dq/dt)₀=-0.022, (dφ/dt)₀=-0.022/(R·exp(-kφ₀)). Los datos son

• Angulo del doble cono, α=30°
• Radio de la base del cono, R=0.15 m
• Angulo mitad entre los raíles, β=20°
• Inclinación, θ=arctan(k)/2

alfa=pi/6;
beta=20*pi/180;
R=0.15; %radio
k=tan(beta)*tan(alfa);
theta=atan(k)/2;
f=@(t,x) [x(2); ((9.8/R)*(k*cos(theta)-sin(theta))*exp(-k*x(1))+
(1+k^2)*k*exp(-2*k*x(1))*x(2)^2)/((1+k^2)*exp(-2*k*x(1))+3/10)];
phi_0=-log(0.01)/k;
dphi_0=-0.022/(R*exp(-k*phi_0));
[t,x]=ode45(f,[0,6],[phi_0, dphi_0]);
q=R*(1-exp(-k*x(:,1)))/k;
plot(t,q)
grid on
xlabel('t')
ylabel('q');
title('Cono doble')

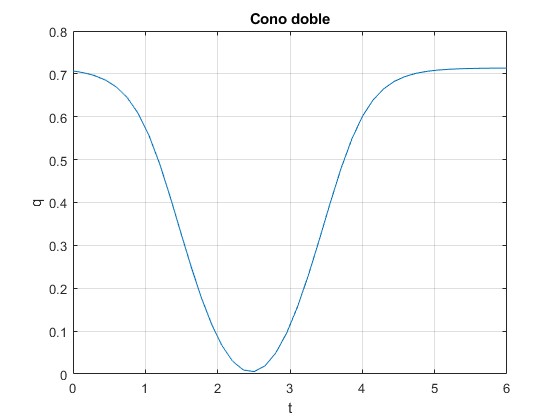
El doble cono se dirige hacia el origen, disminuyendo su velocidad, llega a la posición donde su velocidad nula y regresa, incrementando su velocidad.

Representamos la velocidad dq/dt en función del tiempo t

alfa=pi/6;
beta=20*pi/180;
R=0.15; %radio
k=tan(beta)*tan(alfa);
theta=atan(k)/2;
f=@(t,x) [x(2); ((9.8/R)*(k*cos(theta)-sin(theta))*exp(-k*x(1))+
(1+k^2)*k*exp(-2*k*x(1))*x(2)^2)/((1+k^2)*exp(-2*k*x(1))+3/10)];
phi_0=-log(0.01)/k;
dphi_0=-0.022/(R*exp(-k*phi_0));
[t,x]=ode45(f,[0,6],[phi_0, dphi_0]);
% q=R*(1-exp(-k*x(:,1)))/k;
dq=R*exp(-k*x(:,1)).*x(:,2);
plot(t,dq)
grid on
xlabel('t')
ylabel('dq/dt');
title('Cono doble')

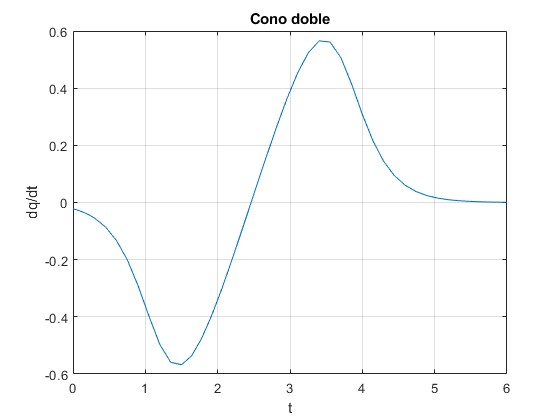
La velocidad se anula, en el instante t en el que q es mínimo

Referencias

Emilio Cortés, D Cortés-Poza. Mechanical paradox: the uphill roller. Eur. J. Phys. 32 (2011) pp. 1559–1576