Movimiento de rodar en el plano horizontal
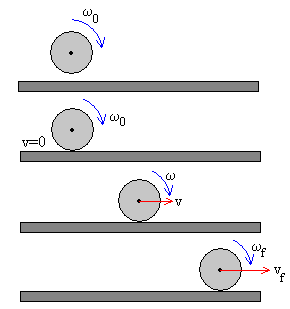
Como se muestra en la figura, una rueda está girando con velocidad angular ω0 alrededor de su eje. Cae sobre un plano horizontal, desliza durante algún tiempo y luego, rueda sin deslizar. Determinaremos la velocidad final vf de su centro de masas y si depende o no del coeficiente de fricción μk entre el plano y la rueda.
Planteamos el problema de modo general. Un disco perfectamente rígido de masa m y de radio R que rueda sobre una superficie horizontal perfectamente rígida. Su velocidad inicial de traslación de su centro de masa v0 y la velocidad angular inicial de rotación alrededor de un eje que pasa por su centro de masa ω0. Determinar la velocidad angular ω, y la velocidad de su centro de masas v, cuando el disco rueda sin deslizar v=ω·R.
Ecuaciones de la dinámica
La única fuerza que actúa sobre el disco es la fuerza de rozamiento Fr en el punto P de contacto con el plano horizontal
Fr=μ·N=μkmg
La velocidad del punto P en un instante cualquiera es
vP=vc-ω ·R
Hay dos posibles casos:
- v0>ω0·R, la fuerza de rozamiento apunta hacia la izquierda
- v0<ω0·R, la fuerza de rozamiento apunta hacia la derecha.
Primer caso, v0>ω0·R
La fuerza de rozamiento apunta hacia la izquierda. La ecuaciones del movimiento serán
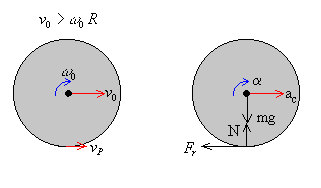
Movimiento de traslación del c.m.
Movimiento de rotación alrededor de un eje que pasa por el c.m.
m·ac=-Fr
Icα =Fr·R
El momento de inercia del disco Ic respecto de un eje perpendicular al disco y que pasa por su centro es
Resolviendo estas dos ecuaciones
La velocidad de traslación del c.m. vc disminuye, aumenta la de rotación ω .
La velocidad del punto P del disco en contacto con el plano horizontal es
vP=vc-ωR=(v0-ω0R)-3μkgt
El movimiento de rodar (sin deslizar) se establece cuando vP=0, es decir en el instante
El desplazamiento s del c.m. y el desplazamiento angular θ, ángulo girado por el disco en el tiempo t son respectivamente
Segundo caso, v0<ω0·R
La fuerza de rozamiento apunta hacia la derecha. Las ecuaciones del movimiento serán
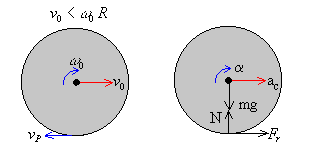
Movimiento de traslación del c.m.
Movimiento de rotación alrededor de un eje que pasa por el c.m.
M·ac=Fr
Icα =-Fr·R
Resolviendo estas dos ecuaciones
La velocidad de traslación del c.m. vc aumenta, la velocidad de rotación ω disminuye
La velocidad del punto P del disco en contacto con el plano horizontal es
vP=vc-ωR=(v0-ω0·R)+3μkgt
El movimiento de rodar (sin deslizar) se establece cuando vP=0, es decir en el instante
El desplazamiento s del c.m. y el desplazamiento angular θ, ángulo girado por el disco en el tiempo t son respectivamente
Condición de rodar (sin deslizar)
Las velocidades finales en el momento en el que se alcanza el estado de movimiento de rodar (sin deslizar) son independientes del coeficiente μk de la fuerza de rozamiento.
En el momento en el que se cumple la condición vc=ω ·R, la fuerza de rozamiento desaparece y el disco comienza una segunda etapa en su movimiento caracterizada por la constancia de la velocidad de traslación del c.m, vc y de la velocidad de rotación ω .
La velocidad final es independiente de la fuerza Fr. En general, las velocidades (de traslación y rotación) en el instante t en el que se establece la condición de rodar sin deslizar son
Cumplen que vc=ω·R. Eliminando la integral (impulso)
La velocidad final de traslación del centro de masas de la rueda (Ic=mR2/2) es
Balance energético
La energía inicial del disco es
La energía final del disco es
Calculamos la diferencia entre la energía final y la inicial, e introducimos en la segunda expresión el valor hallado de vc en el instante t en el que el disco rueda (sin deslizar).
Calculamos ahora el trabajo realizado por la fuerza de rozamiento
- Primer caso, v0>ω0·R
- Segundo caso, v0<ω0·R
La fuerza de rozamiento se opone al movimiento de traslación y favorece el movimiento de rotación
W=-Fr·s+Mr·θ =-mμkg(s-Rθ)
Calculamos los valores de s y θ en el instante t en el que el disco rueda (sin deslizar) y comprobamos, después de hacer algunas operaciones, que
W=Ef-Ei
La fuerza de rozamiento favorece el movimiento de traslación y se opone al movimiento de rotación
W=Fr·s-Mr·θ =-mμkg(-s+Rθ)
Calculamos los valores de s y θ en el instante t en el que el disco rueda (sin deslizar) y comprobamos, después de hacer algunas operaciones, que
W=Ef-Ei
Actividades
Se introduce:
- Velocidad inicial de traslación del c.m. v0 (un número positivo), en el control titulado V. traslación
- Velocidad inicial de rotación alrededor de un eje que pasa por el c.m. ω0 (un número positivo o negativo), en el control titulado V. rotación
- El coeficiente μk de la fuerza de rozamiento por deslizamiento, en el control titulado Coef. rozamiento
- El radio R del disco está fijado por el programa interactivo en R=1
Se pulsa el botón titulado Nuevo.
Observamos el movimiento del disco. Con flechas de color rojo se representan, la velocidad del cm. vc en cada instante y la velocidad del punto P de contacto entre el disco y el plano horizontal vP.
La velocidad vP puede ser inicialmente positiva o negativa dependiendo de que v0>ω0·R ó v0<ω0·R. Al cabo de un cierto tiempo t la velocidad vP se hace cero y el disco rueda (sin deslizar), se cumple entonces vc=ω·R.
En la parte superior derecha, se muestran los siguientes datos:
- Tiempo t
- Velocidad angular de rotación ω
- Velocidad de traslación del c.m. vc
- Velocidad del punto P de contacto del disco con el plano horizontal vP
En la parte superior, se representa en la misma gráfica en función del tiempo t
- En color azul, la velocidad ω·R de rotación
- En color rojo, la velocidad vc de traslación
Observaremos, que dependiendo de que v0>ω0·R ó v0<ω0·R, una de las velocidades se incrementa y la otra disminuye hasta que adquieren un valor común después de un tiempo t.
En la parte superior izquierda, se representa el diagrama de energías.
- La energía inicial dividida en dos sectores angulares
- El sector azul, es la energía cinética de rotación
- El sector rojo, es la energía cinética de traslación
- La energía en cada instante dividida en dos sectores
- El sector azul claro, es la energía cinética de rotación
- El sector rosa, es la energía cinética de traslación
Después de un cierto tiempo t en el que el disco rueda (sin deslizar), la energía cinética de rotación es la tercera parte de la energía total, tal como hemos demostrado en el apartado balance energético. La energía cinética de rotación final está representada por un sector de 120º, mientras que la de traslación está representada por un sector de 240º.
Observamos también, que la energía inicial es mayor que la final, la diferencia se pierde como trabajo de la fuerza de rozamiento.
- Comprobamos que la velocidad final de traslación del c.m. del disco viene dada por
- Comprobamos que el tiempo t que tarda en alcanzarse esta velocidad es
- Que a partir de dicho instante se cumple la condición de rodar (sin deslizar)
vc=ω·R.
Ejemplos
En este apartado, se resuelven cuatro problemas interesantes
Problema 1
Una esfera (Ic=2mr2/5) rueda sin deslizar v0=ω0r, sobre un plano horizontal rugoso (con rozamiento) con velocidad v0=7 m/s hacia un plano vertical liso. Si el coeficiente de restitución entre el plano vertical y la esfera es ε=0.7, calcular la velocidad final de la esfera después de que se restablezca la condición de rodar sin deslizar.
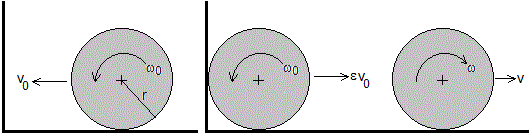
Movimiento de rodar deslizando
Inmediatamente después del choque, la velocidad de traslación del c.m. es εv0, la velocidad angular de rotación ω0=v0/r no ha cambiado. Deja de cumplirse la condición de rodar sin deslizar. Aparece una fuerza de rozamiento Fr=μkN=μkmg que va a restablecer dicha condición
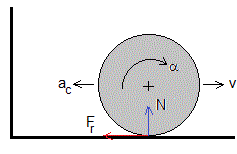
Ecuaciones del movimiento
La velocidad v del centro de masa y la velocidad angular de rotación ω en el instante t son
La condición de rodar sin deslizar v=ωr, se restablece en el instante t
La velocidad final v del centro de masas es
A partir de este instante t, la esfera rueda sin deslizar con velocidad constante
Problema 2
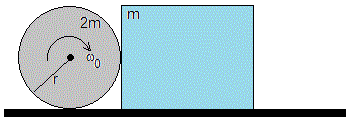
Un bloque de masa m que tiene una altura 2r, está en reposo sobre un plano horizontal. Un cilindro de masa 2r y radio r, está girando alrededor de su eje con velocidad angular ω0. En el instante inicial, t=0, se sitúa sobre el plano horizontal poniéndose en contacto con el bloque.
Supondremos que el sistema formado por el bloque y cilindro están en contacto durante el movimiento posterior.
El coeficiente de rozamiento (estático y cinético) es μ entre los dos cuerpos y plano horizontal, pero no hay rozamiento entre el cilindro y el bloque.
Calcularemos el tiempo T que tarda el cilindro en establecer el movimiento de rodar sin deslizar y el tiempo T' que tarda en detenerse.
Movimiento de rodar deslizando
Representamos las fuerzas sobre el cilindro y sobre el bloque
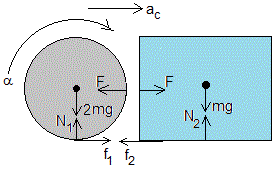
Cilindro
- Peso del cilindro, 2mg
- Fuerza que ejerce el plano horizontal, N1
- Fuerza de rozamiento f1, opuesta al movimiento inicial de rotación
- Fuerza F que ejerce el bloque en el punto de contacto
Bloque
- Peso, mg
- Fuerza que ejerce el plano horizontal, N2
- Fuerza de rozamiento por deslizamiento f2=μN2, opuesta al movimiento del bloque
- Fuerza F que ejerce el cilindro en el punto de contacto
Ecuaciones del movimiento
Cilindro
Bloque
Eliminamos la fuerza F desconocida y despejamos la aceleración ac de traslación del centro del cilindro y del bloque
De la ecuación del movimiento de rotación del cilindro despejamos la aceleración angular α
La velocidad del bloque y cilindro y la velocidad angular del cilindro en el instante t son
La velocidad de traslación del c.m. del cilindro aumenta, la velocidad angular de rotación alrededor de su eje disminuye, hasta el instante T en el que se restablece la condición de rodar sin deslizar vc=ωr
En este instante T, las velocidad del sistema y la angular de rotación del cilindro son
Movimiento de rodar sin deslizar
A partir de este instante, la velocidad del sistema disminuye, mientras se mantiene la condición de rodar sin deslizar del cilindro (ac=αr). En este caso, f'1 es una fuerza de rozamiento desconocida, menor que la máxima μ(2mg). Las ecuaciones del movimiento son
Cilindro
Bloque
Eliminamos la fuerza desconocida F'
De la ecuación del movimiento de rotación del cilindro y la condición de rodar sin deslizar, obtenemos
En el sistema de ecuaciones, eliminamos la fuerza desconocida y despejamos la aceleración del bloque y del centro del cilindro
La velocidad de traslación del centro del cilindro y del bloque en el instante t' es
Se anula (sistema en reposo) en el instante T'
La velocidad angular de rotación del cilindro en el instante t' es
Se anula (el cilindro en reposo) en el instante T'
Ambos tiempos coinciden, como cabría esperar
El tiempo total es
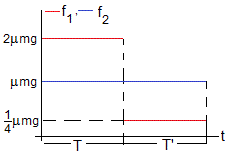
Representamos las fuerzas de rozamiento que ejerce el plano horizontal sobre el clindro, f1 y sobre el bloque f2 en función del tiempo
f2 permenece constante de las dos etapas del movimiento, en ambas, el bloque desliza sobre el plano horizontal
Sin embargo, f1 cambia notablemente. En la primera etapa, el cilindro desliza, en la segunda etapa, el cilindro rueda
Problema 3
Sea un cilindro macizo (I=mr2/2) de masa m y radio r y una plataforma de masa 2m y longitud 12 m que puede deslizar sobre el plano horizontal sin rozamiento. El coeficiente de rozamiento cinético entre el cilindro y la plataforma es μ=0.1
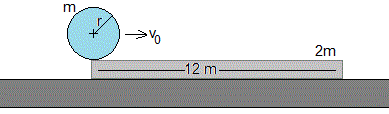
La velocidad del c.m. del cilindro cuando entra en la plataforma es v0=7 m/s, la velocidad angular de rotación es nula, ω0=0.
Calcular el tiempo que tarda el cilindro en recorrer la plataforma (tómese g=10 m/s2)
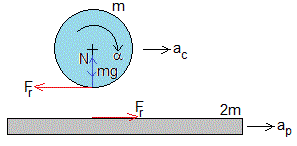
Cuando el cilindro se pone sobre la plataforma, no se cumple la condición de rodar sin deslizar, aparece una fuerza de rozamiento Fr=μN=μmg que restaura dicha condición.
Calculamos la aceleración del c. m. cilindro y la aceleración angular respecto del eje del cilindro
La aceleración de la plataforma es
La aceleración del c.m. del cilindro respecto de la plataforma es
es una aceleración que disminuye la velocidad de traslación del centro de masas. La velocidad de la cilindro respecto de la plataforma es
Por otra parte, la velocidad angular de rotación se incrementa
Se establece la condición de rodar sin deslizar, en el instante t en el que v=ωr
En este tiempo, el c.m. del cilindro se ha desplazado sobre la plataforma
La velocidad del c.m. del cilindro en ese instante t es
Con los datos del problema, v0=7 m/s, μ=0.1, los resultados son: t=2 s, v=4 m/s y x=11 m
Rueda sin deslizar
En el instante t=2 s y en la posición x=11 m sobre la plataforma, se establece la condición de que el cilindro rueda sin deslizar. A partir de ese instante, el cilindro rueda con velocidad constante v=4 m/s tardando un tiempo t=1/4 s en llegar al final de la plataforma.
El tiempo total que el cilindro está sobre la plataforma es t=2+1/4=2.25 s
Problema 4
Sea un esfera maciza (Ic=2mr2/5) de masa m y radio r y una plataforma de masa m, suficientemente larga. La plataforma puede deslizar sobre el plano horizontal sin rozamiento. El coeficiente de rozamiento cinético entre el cilindro y la plataforma es μ
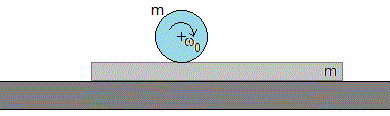
La velocidad angular de la esfera cuando se pone sobre la plataforma es ω0, la velocidad de traslación del c.m. de la esfera es nula, v0=0.
Calcular el desplazamiento de la plataforma hasta el instante en el que se establece la condición de rodar sin deslizar
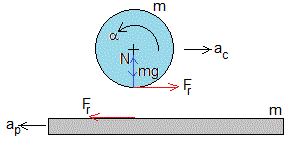
Cuando la esfera se pone sobre la plataforma, no se cumple la condición de rodar sin deslizar, aparece una fuerza de rozamiento Fr=μN=μmg que restaura dicha condición.
Calculamos la aceleración del c. m. de la esfera y su aceleración angular alrededor del eje que pasa por el c.m.
La aceleración de la plataforma es
La aceleración del c.m. de la esfera respecto de la plataforma es
es una aceleración que aumenta la velocidad de traslación del centro de masas. La velocidad de la esfera respecto de la plataforma es
Por otra parte, la velocidad angular de rotación disminuye
Se establece la condición de rodar sin deslizar, en el instante t en el que v=ωr
En este tiempo, la plataforma se ha desplazado hacia la izquierda
Referencias
Indian National Physics Olympiad. Homi Bhabha Centre for Science Eduaction. Solved papers NSEP & INPhO, 2016-2018,
- Ejemplo 19, enunciado, 165, solución, 178
- Ejemplo 13, enunciado, 164, solución, 176-177
- Ejemplo 18, enunciado, 165, solución, 178
Vijay A. Singh, Praveen Pathak. Indian National Physics Olympiad Theory Problems and Solutions (2006 - 2009). pp. 9-10 (enunciado), 53-54 (solución)

