En la página titulada, un cuerpo desliza sobre un plano inclinado móvil, estudiamos un sistema aislado formado por una bloque que desliza sobre una cuña que a su vez, desliza sobre un plano horizontal sin rozamiento.

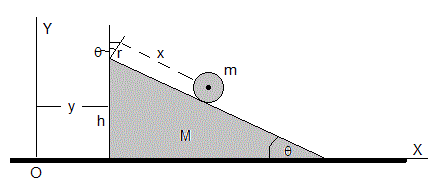
El plano inclinado es una cuña de masa M, que forma un ángulo θ con la horizontal sobre el que desliza sin rozamiento. Un disco de radio r y masa m rueda sin deslizar sobre el plano inclinado.

En un instante dado t, la cuña está en la posición y, y el centro del disco se ha desplazado x a lo largo del plano inclinado. La posición del centro del disco respecto de los ejes X, Y es

x_b=y+rsinθ+xcosθ
y_b=h+rcosθ-xsinθ

Derivando respecto del tiempo t, obtenemos las componentes de la velocidad del centro del disco

${\displaystyle \{\begin{array}{l}\frac{d{x}_b}{dt}=\frac{dy}{dt}+\frac{dx}{dt}\cos \theta \\ \frac{d{y}_b}{dt}=-\frac{dx}{dt}\sin \theta \end{array}}$

La velocidad de la cuña es dy/dt

Sistema aislado

Aplicamos el principio de conservación del momento lineal al sistema aislado formado por el disco y la cuña. El momento lineal se conserva a lo largo del eje X.

Supondremos que en el instante t=0, la cuña y el disco están en reposo en sus posiciones iniciales x=0, e y=0.

${\displaystyle \begin{array}{l}m\left(\frac{dy}{dt}+\frac{dx}{dt}\cos \theta \right)+M\frac{dy}{dt}=0\\ (m+M)\frac{dy}{dt}=-m\frac{dx}{dt}\cos \theta \end{array}}$

Integramos con respecto a t

${\displaystyle y=-\frac{m}{m+M}x\cos \theta }$

Cuando el cilindro llega al vértice de la cuña, x=h/sinθ, ésta se ha desplazado a la izquierda del origen

${\displaystyle y=-\frac{m}{m+M}\frac{h}{\tan \theta }}$

Supongamos que el disco rueda sin deslizar, aplicamos el principio de conservación de la energía. La energía potencial del cilindro se convierte en energía cinética de la cuña y en energía cinética del disco, (suma de la energía cinética de traslación de su centro de masas y de rotación alrededor de un eje que pasa por el centro de masas).

${\displaystyle \begin{array}{l}mgx\sin \theta =\frac{1}{2}M{\left(\frac{dy}{dt}\right)}^2+\frac{1}{2}m\left\{{\left(\frac{d{x}_b}{dt}\right)}^2+{\left(\frac{d{y}_b}{dt}\right)}^2\right\}+\frac{1}{2}I{\omega }^2\\ mgx\sin \theta =\frac{1}{2}M{\left(\frac{dy}{dt}\right)}^2+\frac{1}{2}m\left\{{\left(\frac{dy}{dt}\right)}^2+{\left(\frac{dx}{dt}\right)}^2+2\left(\frac{dy}{dt}\right)\left(\frac{dx}{dt}\right)\cos \theta \right\}+\\ \frac{1}{2}\left(\frac{1}{2}m{r}^2\right){\left(\frac{dx}{dt}\right)}^2\frac{1}{r^2}\\ mgx\sin \theta =\frac{1}{2}(M+m){\left(\frac{dy}{dt}\right)}^2+\frac{3}{4}m{\left(\frac{dx}{dt}\right)}^2+m\left(\frac{dy}{dt}\right)\left(\frac{dx}{dt}\right)\cos \theta \end{array}}$

Introduciendo la relación entre dx/dt y dy/dt resultado de la aplicación del principio de conservación del momento lineal

${\displaystyle \begin{array}{l}mgx\sin \theta =\frac{1}{2}(M+m)\frac{m^2}{{\left(M+m\right)}^2}{\left(\frac{dx}{dt}\right)}^2{\cos }^2\theta +\frac{3}{4}m{\left(\frac{dx}{dt}\right)}^2-m\frac{m}{M+m}\left(\frac{dx}{dt}\right)\cos \theta \left(\frac{dx}{dt}\right)\cos \theta \hfill \\ \begin{array}{l}mgx\sin \theta =\frac{m}{4(M+m)}\left(3M+m(1+2{\sin }^2\theta )\right){\left(\frac{dx}{dt}\right)}^2\\ \frac{dx}{dt}=\sqrt{\frac{4(M+m)g\sin \theta }{3M+m(1+2{\sin }^2\theta )}x}\end{array}\hfill \end{array}}$

Integramos esta ecuación diferencial con las condiciones iniciales, t=0, x=0

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{x}{\int }}\frac{dx}{\sqrt{x}}}=\sqrt{\frac{4(M+m)g\sin \theta }{3M+m(1+2{\sin }^2\theta )}}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ x=\frac{(M+m)g\sin \theta }{3M+m(1+2{\sin }^2\theta )}{t}^2\end{array}}$

Actividades

Se introduce

• El ángulo θ, del plano inclinado, en el control titulado Angulo.
• El cociente m/M, masa del disco m, masa de la cuña, M en el control titulado Masa disco/cuña

Se pulsa el botón titulado Nuevo

Se observa, el movimiento de la cuña y el movimiento del disco a lo largo del plano inclinado. La posición del c.m. del disco, de la cuña y la posición del c.m. del sistema formado por ambos cuerpos. Comprobamos que el c.m. del sistema se encuentra en reposo horizontalmente.

En la parte superior, se nos proporciona los datos del tiempo, aceleración, velocidad, posición del disco respecto de la cuña y de la cuña respecto del sistema de ejes X, Y. Cuando el disco termina su movimiento sobre la cuña se mueve sobre plano horizontal, las posiciones y velocidades del disco se refieren sistema de ejes X, Y.

Ecuaciones de Lagrange

Las ecuaciones de Lagrange nos proporcionan una solución rápida del problema.

Energía cinética

La energía cinética del sistema formado por la esfera y la cuña, que ya hemos obtenido anteriormente, es

${\displaystyle \begin{array}{l}\begin{array}{l}T=\frac{1}{2}M{\left(\frac{dy}{dt}\right)}^2+\frac{1}{2}m\left\{{\left(\frac{d{x}_b}{dt}\right)}^2+{\left(\frac{d{y}_b}{dt}\right)}^2\right\}+\frac{1}{2}I{\omega }^2=\\ \frac{1}{2}m\left\{{\left(\frac{dy}{dt}\right)}^2+{\left(\frac{dx}{dt}\right)}^2+2\left(\frac{dy}{dt}\right)\left(\frac{dx}{dt}\right)\cos \theta \right\}+\frac{1}{2}\left(\frac{1}{2}m{r}^2\right){\left(\frac{dx}{dt}\right)}^2\frac{1}{r^2}=\end{array}\hfill \\ T=\frac{1}{2}(M+m){\left(\frac{dy}{dt}\right)}^2+\frac{3}{4}m{\left(\frac{dx}{dt}\right)}^2+m\left(\frac{dy}{dt}\right)\left(\frac{dx}{dt}\right)\cos \theta \hfill \end{array}}$

Energía potencial

La altura del centro de masas de la cuña no cambia, no se modifica su energía potencial. Si establecemos el origen de la energía en la posición inicial del centro del disco. Cuando se ha desplazado x a lo largo del plano inclinado su energía potencial es V=-mgxsinθ. La lagrangiana L=T-V es

${\displaystyle L=\frac{1}{2}(M+m){\left(\frac{dy}{dt}\right)}^2+\frac{3}{4}m{\left(\frac{dx}{dt}\right)}^2+m\left(\frac{dy}{dt}\right)\left(\frac{dx}{dt}\right)\cos \theta +mgx\sin \theta }$

Ecuaciones del movimiento

Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right)-\frac{\partial L}{\partial x}=0\\ \frac{3}{2}m\frac{d^{2}x}{d{t}^2}+m\frac{d^{2}y}{d{t}^2}\cos \theta -mg\sin \theta =0\\ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{y}}\right)-\frac{\partial L}{\partial y}=0\\ (M+m)\frac{d^{2}y}{d{t}^2}+m\frac{d^{2}x}{d{t}^2}\cos \theta =0\end{array}}$

Despejamos d²x/dt² y d²y/dt² en este sistema de dos ecuaciones e integramos para obtener x e y en función del tiempo t, sabiendo que en el instante t=0, el disco parte de x=0, en reposo dx/dt=0,

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=\frac{2(m+M)g\sin \theta }{3M+m(1+2{\sin }^2\theta )}\\ \frac{dx}{dt}=\frac{2(m+M)g\sin \theta }{3M+m(1+2{\sin }^2\theta )}t\\ x=\frac{(m+M)g\sin \theta }{3M+m(1+2{\sin }^2\theta )}{t}^2\end{array}}$

La cuña parte del origen y=0, en reposo dy/dt=0

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{t}^2}=-\frac{2mg\sin \theta ·\cos \theta }{3M+m(1+2{\sin }^2\theta )}\\ \frac{dy}{dt}=-\frac{2mg\sin \theta ·\cos \theta }{3M+m(1+2{\sin }^2\theta )}t\\ y=-\frac{mg\sin \theta ·\cos \theta }{3M+m(1+2{\sin }^2\theta )}{t}^2\end{array}}$

La relación entre x e y es

${\displaystyle y=-\frac{m}{m+M}x\cos \theta }$

Que ya habíamos obtenido anteriormente, aplicando el principio de conservación del momento lineal