Sea una barra de masa m, longitud l y anchura δ, se coloca simétricamente sobre una cúpula de forma semiesférica de radio R. El punto B de la barra coincide con el punto A del vértice de la semiesfera cuando la barra parte de la posición horizontal de equilibrio, θ=0

La barra se desplaza un ángulo θ, la barra es tangente a la semicircunferencia en P, la distancia BP es el arco de circunferencia AP=Rθ

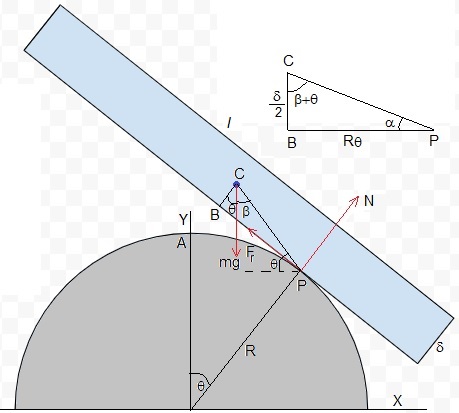
La posición del punto B es,

x_B=Rsinθ-BP·cosθ=R(sinth-θ·cosθ),
y_B=Rcosθ+BP·sinθ=R(cosθ+θ·sinθ)

La posición del centro de masas C es,

x_C=x_B+(δ/2)sinθ=R(sinθ-θ·cosθ)+(δ/2)sinθ
y_C=y_B+(δ/2)cosθ=R(cosθ+θ·sinθ)+(δ/2)cosθ

La velocidad del centro de masas es

${\displaystyle \begin{array}{l}\frac{d{x}_c}{dt}=\left(R\theta ·\sin \theta +\frac{\delta }{2}\cos \theta \right)\frac{d\theta }{dt}\\ \frac{d{y}_c}{dt}=\left(R\theta ·\cos \theta -\frac{\delta }{2}\sin \theta \right)\frac{d\theta }{dt}\end{array}}$

Fuerzas

Las fuerzas que actúan sobre la barra son:

• el peso, mg en el centro de masa

• La reacción N y la fuerza de rozamiento F_r en el punto de contacto P

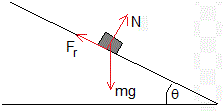
Sea μ_s el coeficiente estático de la fuerza de rozamiento entre el cuerpo de masa m y el plano inclinado de ángulo θ.

El cuerpo empieza a deslizar cuando la componente del peso a lo largo del plano inclinado mgsinθ se hace igual o mayor que máximo valor de la fuerza de rozamiento μ_sN. El ángulo límite del plano inclinado es, mgsinθ=μ_smgcosθ. Simplificando, tanθ_l=μ_s.

Si θ≥θ_l el cuerpo desliza, en caso contrario permenece en reposo

A partir del ángulo θ_l la barra desliza a lo largo de la cúpula semiesférica

En esta página, supondremos que el coeficiente estático μ_s es suficientemente grande para que la barra no deslice durante su movimiento oscilatorio

Momento

El peso mg ejerce un momento respecto del punto de contacto P, que hace que la barra retorne a la posición de equilibrio θ=0

M=mg·PC·sinβ.

En el triángulo rectángulo PBC relacionamos los ángulos α, β y θ. β=π/2-α-θ

M=mg·PC·cos(α+θ)=mg(PC·cosα·cosθ-PC·sinα·sinθ)=mg(Rθ·cosθ-(δ/2)sinθ).

El momento es nulo cuando θ=0, en la posición de equilibrio y vuelve a ser nulo cuando el centro de masas C está encima del punto de contacto P, es decir, cuando x_C=x_P

R(sinθ-θ·cosθ)+(δ/2)sinθ=Rsinθ
-Rθcosθ+(δ/2)sinθ=0
(δ/2)tanθ=Rθ

Representamos

${\displaystyle M=mg\frac{\delta }{2}\left(k\theta \cos \theta -\sin \theta \right),k=\frac{R}{\delta /2}}$

para un radio de la cúpula R=3.5 cm, y para una anchura de la barra δ=1 cm, lo que determina el valor del parámetro adimensional, k=7

R=0.035; %radio de la cúpula semiesférica
delta=0.01; %anchura de la barra
k=R/(delta/2); %parámetro 
f=@(x) k*x.*cos(x)-sin(x); 
fplot(f,[0,pi/2])
th_m=fzero(f,[0.1,pi/2]); %ángulo, momento nulo
line([th_m,th_m],[-1,0],'lineStyle','--','color','k')
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
xlabel('\theta')
ylabel('M')
title('Momento del peso')

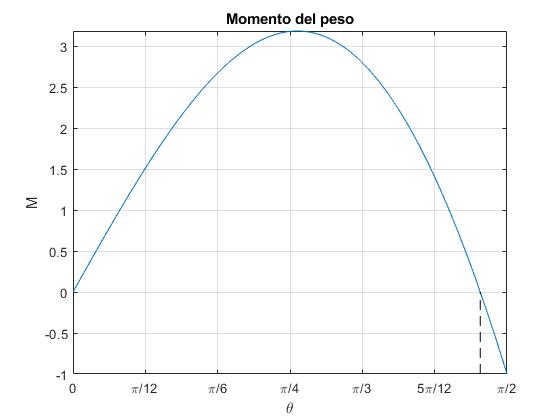
>> th_m*180/pi
ans =   84.4650

En la figura, señalamos el ángulo θ_m=84.5° para el cual el momento M es nulo. Para ello resolvemos la ecuación transcendente kθ·cosθ-sinθ=0, utilizando la función fzero de MATLAB

Energía potencial

Establecemos el nivel cero de energía potencial en la posición del centro de masas, cuando la barra está en equilibrio, θ=0, x_C=0, y_C=R+δ/2

E_p(θ)=mgy_C-mg(R+δ/2)=mg(R(cosθ+θ·sinθ)+(δ/2)cosθ)-mg(R+δ/2)

${\displaystyle E_p(\theta )=mg\frac{\delta }{2}\left(k\left(\theta ·\sin \theta +\cos \theta -1\right)+\cos \theta -1\right)}$

La energía potencial presenta un máximo

${\displaystyle \frac{d{E}_p(\theta )}{d\theta }=mg\frac{\delta }{2}\left(k\theta ·\cos \theta -\sin \theta \right)=0}$

para el mismo ángulo θ_m que hace que el momento sea nulo

Representamos la energía potencial para varios valores del parámetro k

hold on
for k=[10,5,4,3,2,1.5] %parámetro
    f=@(x) k*(x.*sin(x)+cos(x)-1)+cos(x)-1;
    fplot(f,[0,pi/2])
    th_m=fzero(@(x) k*x*cos(x)-sin(x),[0.1,pi/2]);
    plot(th_m,f(th_m),'o','markersize',3,'markeredgecolor','r',
'markerfacecolor','r')
end
hold off
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
xlabel('\theta')
ylabel('E_p(\theta)')
title('Energía potencial')

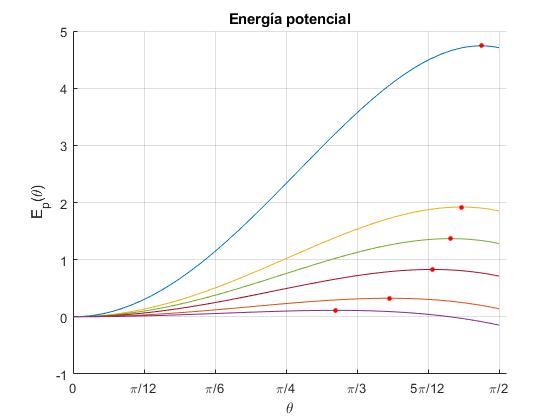
Un punto de color rojo señala el máximo de la energía potencial, E_p(θ)

Energía cinética

La energía cinética de la barra es la suma de la energía cinética de traslación del centro de masas y de rotación alrededor de un eje perpendicular al plano de la figura y que pasa por el c.m.

${\displaystyle E_k=\frac{1}{2}m\left\{{\left(\frac{d{x}_c}{dt}\right)}^2+{\left(\frac{d{y}_c}{dt}\right)}^2\right\}+\frac{1}{2}{I}_c{\left(\frac{d\theta }{dt}\right)}^2=\frac{1}{2}m\left(R^2{\theta }^2+{\left(\frac{\delta }{2}\right)}^2\right){\left(\frac{d\theta }{dt}\right)}^2+\frac{1}{2}{I}_c{\left(\frac{d\theta }{dt}\right)}^2}$

Se trata de un sistema conservativo, la energía permanece constante

${\displaystyle E=\frac{1}{2}\left\{m\left(R^2{\theta }^2+{\left(\frac{\delta }{2}\right)}^2\right)+I_c\right\}{\left(\frac{d\theta }{dt}\right)}^2+mg\left\{R\left(\cos \theta +\theta \sin \theta \right)+\frac{\delta }{2}\cos \theta \right\}-mg\left(R+\frac{\delta }{2}\right)}$

El momento de inercia I_c=ml²/12, de una varilla respecto de un eje perpendicular a la misma y que pasa por el centro de masas

Descripción cualitativa del movimiento

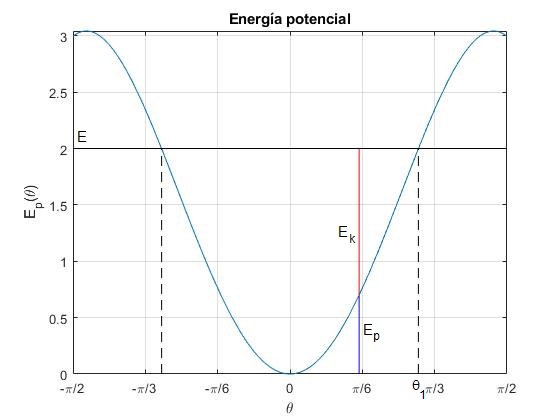
Representamos la energía potencial E_p(θ), para el valor del parámetro k=7. Sea E=2 la energía total en unidades mgδ/2, menor que el máximo de la energía potencial. La barra oscila entre dos posiciones extremas θ₁ y -θ₁.

Para una posición θ=0.5 rad, el segmento de color azul señala la energía potencial y el rojo la energía cinética. A medida que se desplaza hacia la derecha la energía potencial aumenta y la cinética disminuye, hasta que en la posición de retorno θ₁ la velocidad angular dθ/dt se hace nula

k=7; %parámetro
f=@(x) k*(x.*sin(x)+cos(x)-1)+cos(x)-1;
fplot(f,[-pi/2,pi/2])
E=2; %energía total
g=@(x) f(x)-E;
th_1=fzero(g,[0.1,pi/2]);
line([-pi/2,pi/2],[f(th_1),f(th_1)],'color','k')
line([-th_1,-th_1],[0,f(th_1)],'color','k','lineStyle','--')
line([th_1,th_1],[0,f(th_1)],'color','k','lineStyle','--')
th=0.5;
line([th,th],[0,f(th)],'color','b') %energía potencial
line([th,th],[f(th),E],'color','r') %energía cinética
set(gca,'XTick',-pi/2:pi/6:pi/2)
set(gca,'XTickLabel',{'-\pi/2','-\pi/3','-\pi/6', '0','\pi/6','\pi/3','\pi/2'})
grid on
xlabel('\theta')
ylabel('E_p(\theta)')
title('Energía potencial')

Ecuación del movimiento

La lagrangiana L=E_k-E_p(θ) es

${\displaystyle L=\frac{1}{2}\left\{m\left(R^2{\theta }^2+{\left(\frac{\delta }{2}\right)}^2\right)+I_c\right\}{\left(\frac{d\theta }{dt}\right)}^2-mg\left\{R\left(\cos \theta +\theta \sin \theta \right)+\frac{\delta }{2}\cos \theta \right\}+mg\left(R+\frac{\delta }{2}\right)}$

La ecuación del movimiento

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \left\{m\left(R^2{\theta }^2+{\left(\frac{\delta }{2}\right)}^2\right)+\frac{1}{12}m{l}^2\right\}\frac{d^2\theta }{d{t}^2}+m{R}^2\theta {\left(\frac{d\theta }{dt}\right)}^2+mg\left(R\theta \cos \theta -\frac{\delta }{2}\sin \theta \right)=0\\ \left\{k^2{\theta }^2+1+\frac{1}{12}\frac{l^2}{{\left(\frac{\delta }{2}\right)}^2}\right\}\frac{d^2\theta }{d{t}^2}+k^2\theta {\left(\frac{d\theta }{dt}\right)}^2+\frac{g}{\frac{\delta }{2}}\left(k\theta \cos \theta -\sin \theta \right)=0\end{array}}$

Resolvemos la ecuación diferencial del movimiento por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, θ=θ₀, (dθ/dt)₀=0. Parte del resposo desde la posición angular θ₀

• Longitud de la barra, l=20 cm
• Anchura de la barra, δ=1 cm
• Radio de la cúpula semiesférica, R=3.5 cm

Con estos datos determinamos el valor del parámetro k=R/(δ/2)=7

L=0.2; %longitud barra
R=0.035; %radio cúpula semiesférica
delta=0.01; %abchura de la barra
k=R/(delta/2); %parámetro
k2=L^2/(delta/2)^2;
k3=9.8/(delta/2);

f=@(t,x) [x(2); -(k^2*x(1)*x(2)^2+k3*(k*x(1)*cos(x(1))-sin(x(1))))
/(k^2*x(1)^2+1+k2/12)]; 
[t,x]=ode45(f,[0,5],[1,0]);
plot(t, x(:,1))
set(gca,'YTick',-pi/3:pi/12:pi/3)
set(gca,'YTickLabel',{'-\pi/3','-\pi/4','-\pi/6','-\pi/12' '0','\pi/12',
'\pi/6','\pi/4','\pi/3'})
grid on
xlabel('t')
ylabel('\theta')
title('Movimiento de la barra')

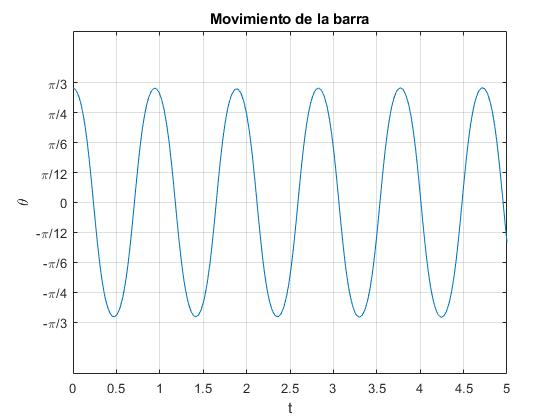
El periodo de las oscilaciones depende de la amplitud, como puede comprobarse, cambiando el ángulo inicial θ₀

Actividades

Se introduce

• El valor del parámetro k=R/(δ/2), en el control titulado Constante
• La posición inicial θ₀ de la barra (parte del reposo), en el control titulado Posición inicial
• La longitud de la barra se ha fijado en, l=20 cm
• El radio de la cúpula semiesférica se ha fijado en, R=3.5 cm

Se pulsa el botón titulado Nuevo. El ángulo inicial θ₀ tiene que ser menor que el ángulo θ_m del máximo de la energía potencial E_p(θ) o del ángulo para el cual el momento del peso mg respecto del punto P de contacto es nulo.

En el caso de que sea mayor, el programa interactivo se detiene y un mensaje nos invita a modificar los datos de entrada

Observamos el movimiento de la barra sobre la cúpula semiesférica, en la parte superior derecha se proporcionan los datos de

• el tiempo, t
• la posicón angular θ en grados
• la velocidad angular dθ/dt en rad/s

Con la ayuda de los botones Pausa y Paso se puede medir el periodo de la oscilación

El programa calcula en cada instante el tanto por ciento de error relativo en la energía o el cociente

${\displaystyle \left|\frac{E-E_0}{E_0}\right|·100}$

donde E es la energía del sistema en cualquier instante t, y E₀ es la energía inicial del sistema.

Este valor se proporciona en caracteres de color rojo. Su valor debe ser siempre cero, o un valor muy pequeño lo que indica que la energía del sistema permanece constante y el programa realiza los cálculos correctamente.

Referencias

M. A. F. Gomes, Wm. R. Savage, Anderson S. L. Gomes. Local stability: An elementary demostration and discussion. Am. J. Phys. 51 (7) July 1983, pp. 636-641