La rueda de Maxwell
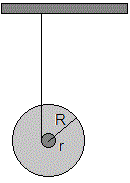
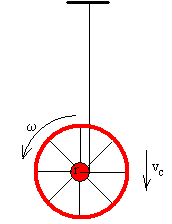
Una cuerda está enrollada en el eje de un disco de masa m y radio R. Se sujeta la cuerda por su extremo y se suelta el disco. Veremos como el disco cae a la vez que va girando sobre su eje. El movimiento del disco es similar al de un juguete popular hace años denominado "yo-yo", o a la denominada rueda de Maxwell, que se utiliza en una práctica de laboratorio para comprobar la conservación de la energía.
Examinaremos en esta página, las ecuaciones del movimiento del disco y aplicaremos el principio de conservación de la energía.
Ecuaciones del movimiento
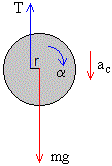
Sobre el disco actúan dos fuerzas: el peso en el centro del disco, y la tensión de la cuerda a una distancia r del centro del disco.
Las ecuaciones del movimiento son:
Movimiento de traslación del centro de masa
Movimiento de rotación alrededor de un eje que pasa por el centro de masas
Relación entre las aceleraciones en el movimiento de traslación ac y en el movimiento de rotación α.
mg-T=mac
T·r=Icα
ac=α·r
Para un disco de masa m y radio R, el momento de inercia Ic=mR2/2. Con este dato calculamos la aceleración ac.
Por medio de las ecuaciones del movimiento rectilíneo uniformemente acelerado calculamos la velocidad y el tiempo que tarda el disco en caer una altura h, partiendo del reposo.
Por ejemplo, para un disco de radio R=6 cm, con un eje de radio r=3 mm. Se obtiene ac=0.049 m/s2. Cuando el disco se deja caer desde una altura h=50 cm, la velocidad angular de rotación de la rueda es vc=ω·r, por lo que ω=73.6 rad/s.
Principio de conservación de la energía
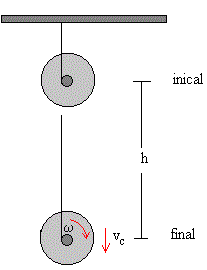
Para aplicar el principio de conservación de la energía comparamos la situación inicial, el disco está en reposo con la situación final, el disco ha descendido una altura h. En la situación final, el centro de masas del disco se mueve con velocidad vc y gira alrededor de un eje que pasa por el centro de masas con velocidad angular ω .
La energía potencial del disco ha disminuido en la cantidad mgh.
La energía cinética del disco ha aumentado en
El principio de conservación de la energía se escribe
La relación entre las velocidades en los movimientos de traslación vc del c.m. del disco y de rotación ω es vc=ω·r
Por ejemplo, para un disco de radio R=6 cm, con un eje de radio r=3 mm. Cuando el disco se deja caer desde una altura h=50 cm, la velocidad angular de rotación de la rueda es ω=73.6 rad/s
Rebote cuando llega al final de la cuerda
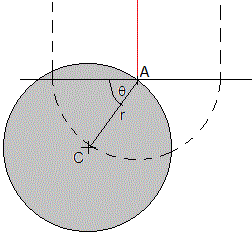
Cuando el disco alcanza el final de la cuerda, realiza un movimiento de rotación alrededor de un punto fijo A, (extremo de la cuerda) tal como se puede ver en la figura. El centro del disco C describe un movimiento semicircular de radio r. Cuando θ=0, la velocidad angular del disco ω0 es la calculada en el apartado anterior. Cuando θ=π, la velocidad angular del disco será la misma.
Cuando θ=π/2, la velocidad angular alcanza su valor máximo que obtenemos aplicando el principio de conservación de la energía
La tensión de la cuerda se obtiene aplicando en este instante, la ecuación de la dinámica del movimiento circular uniforme. T-mg=mω2r
Como r es pequeño, la velocidad angular de rotación ω=73.82 rad/s, difiere poco de ω0. La tensión de la cuerda será T=26.15·m N, siendo m la masa del disco
Las ecuaciones que hemos empleado para describir el movimiento descendente del disco, son válidas para describir su ascenso, solamente hemos de observar que:
- La energía cinética (de rotación y de traslación) del disco disminuye y aumenta la energía potencial del c.m. del disco. La energía total se mantiene constante.
- La tensión de la cuerda T ejerce un momento T·r que se opone al movimiento de rotación del disco.
- La resultante de las fuerzas que actúan sobre el disco mg-T se opone al movimiento de traslación del c.m.
Actividades
Cuando r=R la velocidad final del centro de masas es independiente de la masa y del radio del disco
Se pulsa el botón titulado Nuevo y a continuación, ►.
Midiendo el tiempo que tarda en caer el disco una determinada altura, se calcula la velocidad de traslación del disco.
Se representa la energía mediante un diagrama de barras.
- La energía potencial en color gris
- La energía cinética de traslación del c.m. en color azul
- La energía cinética de rotación del disco en color rojo
Cuando disminuye la energía potencial aumenta la energía cinética y cuando aumenta la energía potencial disminuye la energía cinética. La energía cinética de rotación es la tercera parte de la energía cinética total.
Práctica de laboratorio
Conocida la altura h y el tiempo t de caída se determina la velocidad de traslación vc del centro de masas cuando la rueda llega al final de su recorrido.
Aplicamos el principio de conservación de la energía
La relación entre la velocidad de traslación del c.m. vc y la de rotación ω alrededor de un eje que pasa por el c.m. es
vc=ω·r
Pesamos la rueda en una balanza, y con un micrómetro medimos el diámetro del eje de la rueda, tal como se ve en la figura. En este eje se enrolla la cuerda

| Altura h (m) | 0.67 |
| Tiempo t (s) | 7.02 |
| Velocidad vc (m/s) | 0.19 |
| Radio r (m) | 0.0025 |
| Masa m (kg) | 0.512 |
| Momento de inercia Ic (kg·m2) | 0.00115 |
|---|
Referencias
Problema de la XIX Olimpiada Internacional de Física. Bad Ischl (Austria), 1988

