Un cilindro rueda sin deslizar sobre una cúpula cóncava móvil

Principios de conservación

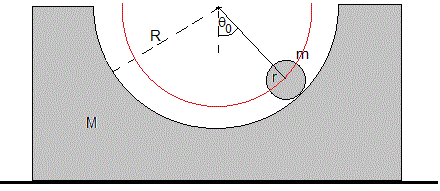
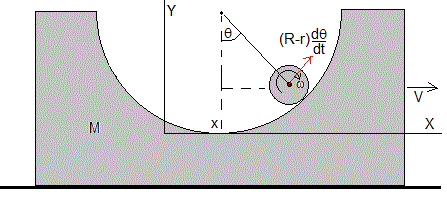
En la figura, observamos la posición inicial de un cilindro de masa m y de radio r que se suelta en la posición angular θ₀, rueda sin deslizar a lo largo de la cúpula. En el instante t la velocidad de su centro de masa es (R-r)dθ/dt, cuya dirección es tangente a la circunferencia de radio R-r

La cúpula de masa M y radio R desliza sobre el plano horizontal sin rozamiento. En el instante inicial t=0 está en reposo y en el instante t lleva una velocidad V

Conservación de la energía

La energía total se mantiene constante e igual a la inicial

$E_{0} = m g R (1 - \cos θ_{0})$

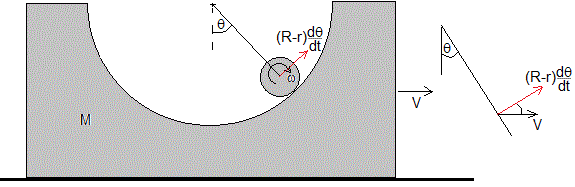
En el instante t, la velocidad de la cúpula es V en la dirección horizontal, la velocidad relativa del c. m. del cilindro respecto de la cúpula invertida es (R-r)dθ/dt, en la dirección tangencial. La velocidad del c. m. del cilindro respecto del Sistema de Referencia Inercial, es la suma vectorial de estas dos velocidades como se indica en la parte derecha de la figura.

La energía cinética del cilindro es la suma de la energía cinética de traslación del centro de masas y la energía cinética de rotación alrededor del eje que pasa por su centro con velocidad angular ω

$\frac{1}{2} m {{(R \frac{d θ}{d t} + V \cos θ)}^{2} + V^{2} \sin^{2} θ} + \frac{1}{2} (\frac{1}{2} m r^{2}) ω^{2}$

La energía potencial de la partícula es mg(R-r)(1-cosθ)

La energía cinética de la cúpula es MV²/2

La energía en el instante t es

$E = \frac{1}{2} m {{(R \frac{d θ}{d t} + V \cos θ)}^{2} + V^{2} \sin^{2} θ} + \frac{1}{2} M V^{2} + \frac{1}{2} (\frac{1}{2} m r^{2}) ω^{2} + m g (R - r) (1 - \cos θ)$

La condición de de que el cilindro ruede sin deslizar es

$(R - r) \frac{d θ}{d t} = ω r$

Igualamos la energía inicial a la energía del sistema en el instante t

$\begin{array}{l} m g (R - r) (1 - \cos θ_{0}) = \frac{1}{2} m {{(R - r)}^{2} {(\frac{d θ}{d t})}^{2} + 2 (R - r) \frac{d θ}{d t} V \cos θ} + \frac{1}{2} (M + m) V^{2} + \frac{1}{4} m {(R - r)}^{2} {(\frac{d θ}{d t})}^{2} + m g (R - r) (1 - \cos θ) \\ m g (R - r) (\cos θ - \cos θ_{0}) = \frac{3}{4} m {(R - r)}^{2} {(\frac{d θ}{d t})}^{2} + m (R - r) \frac{d θ}{d t} V \cos θ + \frac{1}{2} (M + m) V^{2} \end{array}$

Conservación del momento lineal

El peso y la reacción del plano horizontal sobre el que desliza la cúpula son las fuerzas externas que actúan sobre el sistema formado por el cúpula semiesférica y el cilindro. No hay fuerzas externas en la dirección horizontal por lo que el momento lineal en esta dirección, se conserva

$\begin{array}{l} m (V + (R - r) \frac{d θ}{d t} \cos θ) + M V = 0 \\ V = - \frac{m}{m + M} (R - r) \frac{d θ}{d t} \cos θ \end{array}$

(R-r)·(dθ/dt)cosθ es la componente horizontal de la velocidad relativa del c m. del cilindro. Véase la figura

En este sistema de dos ecuaciones, eliminamos la velocidad de la cúpula V y despejamos la velocidad relativa (R-r)·dθ/dt del c. m. del cilindro

$\begin{array}{l} m g (R - r) (\cos θ - \cos θ_{0}) = \frac{3}{4} m {(R - r)}^{2} {(\frac{d θ}{d t})}^{2} + m (R - r) \frac{d θ}{d t} (- \frac{m}{m + M} (R - r) \frac{d θ}{d t} \cos θ) \cos θ + \frac{1}{2} (M + m) {(- \frac{m}{m + M} (R - r) \frac{d θ}{d t} \cos θ)}^{2} \\ g (\cos θ - \cos θ_{0}) = \frac{3}{4} (R - r) {(\frac{d θ}{d t})}^{2} - \frac{1}{2} \frac{m}{m + M} (R - r) {(\frac{d θ}{d t})}^{2} \cos^{2} θ \\ (R - r) {(\frac{d θ}{d t})}^{2} = \frac{4 (m + M) g (\cos θ - \cos θ_{0})}{3 M + m + m \sin^{2} θ} \end{array}$

Ecuaciones del movimiento

Ecuaciones del movimiento del cilindro

Las fuerzas que actúan sobreel cilindro son

el peso mg
la reacción de la cúpula N, la fuerza que ejerce la cúpula sobre el cilindro
La fuerza de rozamiento, F_r<μ_sN

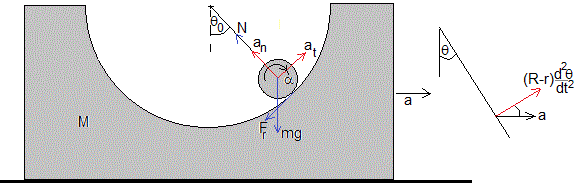
El c. m. del cilindro describe un movimiento circular de radio R-r con aceleraciones relativas

En la dirección tangencial, $a_{t} = (R - r) \frac{d^{2} θ}{d t^{2}}$
En la dirección normal, $a_{n} = (R - r) {(\frac{d θ}{d t})}^{2}$

A estas aceleraciones hay que sumarle vectorialmente la aceleración a de la cúpula

La ecuación del movimiento de traslación del c. m. en la dirección tangencial es

$m ((R - r) \frac{d^{2} θ}{d t^{2}} + a \cos θ) = - m g \sin θ - F_{r}$

La ecuación del movimiento del traslación del c. m. en la dirección normal es

$m ((R - r) {(\frac{d θ}{d t})}^{2} - a \sin θ) = N - m g \cos θ$

La ecuación del movimiento de rotación alrededor del eje que pasa por su c. m.

$\begin{array}{l} I α = F_{r} r \\ (\frac{1}{2} m r^{2}) α = F_{r} r \\ F_{r} = \frac{1}{2} m r α \end{array}$

La condición de que el cilindro rueda sin deslizar

$\begin{array}{l} (R - r) \frac{d^{2} θ}{d t^{2}} = r α \\ F_{r} = \frac{1}{2} m (R - r) \frac{d^{2} θ}{d t^{2}} \end{array}$

Ecuación del movimiento de la cúpula

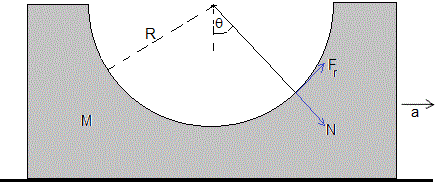
La fuerza que ejerce el cilindro sobre la cúpula es N y F_r pero de sentido contrario. La ecuación del movimiento de la cúpula es

$M a = N \sin θ + F_{r} \cos θ$

Sustituimos la fuerza de rozamiento F_r en la ecuación del movimiento de la cúpula y en la ecuación del movimiento del c. m. en la dirección tangencial

$\begin{array}{l} M a = N \sin θ + \frac{1}{2} m (R - r) \frac{d^{2} θ}{d t^{2}} \cos θ \\ m (R - r) \frac{d^{2} θ}{d t^{2}} + m a \cos θ = - m g \sin θ - \frac{1}{2} m (R - r) \frac{d^{2} θ}{d t^{2}} \\ \frac{3}{2} m (R - r) \frac{d^{2} θ}{d t^{2}} + m a \cos θ = - m g \sin θ \end{array}$

Despejamos la reacción N en la primera de estas dos últimas ecuaciones y la sustituimos en la ecuación del movimiento en la dirección normal. A continuación, despejamos la aceleración a de la cúpula

$\begin{array}{l} m (R - r) {(\frac{d θ}{d t})}^{2} - m a \sin θ = \frac{M a - \frac{1}{2} m (R - r) \frac{d^{2} θ}{d t^{2}} \cos θ}{\sin θ} - m g \cos θ \\ m (R - r) {(\frac{d θ}{d t})}^{2} \sin θ - m a \sin^{2} θ = M a - \frac{1}{2} m (R - r) \frac{d^{2} θ}{d t^{2}} \cos θ - m g \cos θ \sin θ \\ a (M + m \sin^{2} θ) = m (R - r) {(\frac{d θ}{d t})}^{2} \sin θ + \frac{1}{2} m (R - r) \frac{d^{2} θ}{d t^{2}} \cos θ + m g \cos θ \sin θ \\ a = \frac{m (R - r) {(\frac{d θ}{d t})}^{2} \sin θ + \frac{1}{2} m (R - r) \frac{d^{2} θ}{d t^{2}} \cos θ + m g \cos θ \sin θ}{M + m \sin^{2} θ} \end{array}$

Sustituimos la aceleración a de la cúpula en la ecuación del movimiento del c. m. en la dirección tangencial

$\begin{array}{l} \frac{3}{2} (R - r) \frac{d^{2} θ}{d t^{2}} + \frac{m (R - r) {(\frac{d θ}{d t})}^{2} \sin θ + \frac{1}{2} m (R - r) \frac{d^{2} θ}{d t^{2}} \cos θ + m g \cos θ \sin θ}{M + m \sin^{2} θ} \cos θ = - g \sin θ \\ \frac{3}{2} (R - r) (M + m \sin^{2} θ) \frac{d^{2} θ}{d t^{2}} + \frac{1}{2} m (R - r) \frac{d^{2} θ}{d t^{2}} \cos^{2} θ + m (R - r) {(\frac{d θ}{d t})}^{2} \sin θ \cos θ + m g \cos^{2} θ \sin θ + (M + m \sin^{2} θ) g \sin θ = 0 \\ (R - r) (\frac{3}{2} (M + m \sin^{2} θ) + \frac{1}{2} m \cos^{2} θ) \frac{d^{2} θ}{d t^{2}} + m (R - r) {(\frac{d θ}{d t})}^{2} \sin θ \cos θ + (M + m) g \sin θ = 0 \end{array}$

Llegando a la ecuación diferencial

$(R - r) (\frac{3 M + m + m \sin^{2} θ}{2}) \frac{d^{2} θ}{d t^{2}} + m (R - r) {(\frac{d θ}{d t})}^{2} \sin θ \cos θ + (M + m) g \sin θ = 0$

Resolveremos esta ecuación del movimiento mediante procedimientos numéricos, sabiendo que en el instante t=0, el c. m. del cilindro parte de la posición θ=θ₀, en reposo.

Ecuaciones de Lagrange

Posición

La posición del centro de la cúpula semiesférica y del c. m. del cilindrorespecto del Sistema de Referencia Inercial

${\begin{cases} \vec{r_{c}} = x \hat{i} \\ \vec{r_{p}} = (x + (R - r) \sin θ) \hat{i} + (R - (R - r) \cos θ) \hat{j} \end{cases}$

Velocidad

Derivando respecto del tiempo obtenemos el vector velocidad de la cúpula y del c. m. del cilindro

${\begin{cases} \vec{V} = \frac{d x}{d t} \hat{i} \\ \vec{v} = (\frac{d x}{d t} + (R - r) \cos θ \frac{d θ}{d t}) \hat{i} + (R - r) \sin θ \frac{d θ}{d t} \hat{j} \end{cases}$

La energía cinética del cilindro (traslación del c. m. y rotación) y de la cúpula

$\begin{array}{l} E_{k} = \frac{1}{2} M {(\frac{d x}{d t})}^{2} + \frac{1}{2} m {{(\frac{d x}{d t} + (R - r) \cos θ \frac{d θ}{d t})}^{2} + {((R - r) \sin θ \frac{d θ}{d t})}^{2}} + \frac{1}{2} (\frac{1}{2} m r^{2}) ω^{2} = \\ \frac{1}{2} (m + M) {(\frac{d x}{d t})}^{2} + \frac{1}{2} m {(R - r)}^{2} {(\frac{d θ}{d t})}^{2} + m (R - r) \cos θ \frac{d x}{d t} \frac{d θ}{d t} + \frac{1}{4} m {(R - r)}^{2} {(\frac{d θ}{d t})}^{2} = \\ \frac{1}{2} (m + M) {(\frac{d x}{d t})}^{2} + \frac{3}{4} m {(R - r)}^{2} {(\frac{d θ}{d t})}^{2} + m (R - r) \cos θ \frac{d x}{d t} \frac{d θ}{d t} \end{array}$

La energía potencial del c. m. del cilindro

$E_{p} = m g (R - r) (1 - \cos θ)$

La lagrangiana

$L = E_{k} - E_{p} = \frac{1}{2} (m + M) {(\frac{d x}{d t})}^{2} + \frac{3}{4} m {(R - r)}^{2} {(\frac{d θ}{d t})}^{2} + m (R - r) \cos θ \frac{d x}{d t} \frac{d θ}{d t} - m g (R - r) + m g (R - r) \cos θ$

Las ecuaciones del movimiento

$\begin{array}{l} \frac{d}{d t} (\frac{\partial L}{\partial \dot{x}}) - \frac{\partial L}{\partial x} = 0 \\ \frac{d}{d t} ((m + M) (\frac{d x}{d t}) + m (R - r) \cos θ \frac{d θ}{d t}) = 0 \end{array}$

Hay una cantidad que se mantiene constante e igual a su valor inicial, el momento lineal horizontal, que es nulo, ya que el c. m. del cilindro y la cúpula estan en reposo en el instante t=0

$(m + M) \frac{d x}{d t} + m (R - r) \cos θ \frac{d θ}{d t} = 0$

La segunda ecuación del movimiento es

$\begin{array}{l} \frac{d}{d t} (\frac{\partial L}{\partial \dot{θ}}) - \frac{\partial L}{\partial θ} = 0 \\ \frac{d}{d t} (\frac{3}{2} {(R - r)}^{2} \frac{d θ}{d t} + (R - r) \cos θ \frac{d x}{d t}) + (R - r) \sin θ \frac{d x}{d t} \frac{d θ}{d t} + g (R - r) \sin θ = 0 \\ \frac{3}{2} {(R - r)}^{2} \frac{d^{2} θ}{d t^{2}} - (R - r) \sin θ \frac{d x}{d t} \frac{d θ}{d t} + (R - r) \cos θ \frac{d^{2} x}{d t^{2}} + (R - r) \sin θ \frac{d x}{d t} \frac{d θ}{d t} + g (R - r) \sin θ = 0 \\ \frac{3}{2} {(R - r)}^{2} \frac{d^{2} θ}{d t^{2}} + (R - r) \cos θ \frac{d^{2} x}{d t^{2}} + g (R - r) \sin θ = 0 \end{array}$

Derivamos la ecuación de la conservación del momento lineal respecto del tiempo

$\begin{array}{l} (m + M) \frac{d^{2} x}{d t^{2}} + m (R - r) \cos θ \frac{d^{2} θ}{d t^{2}} - m (R - r) \sin θ {(\frac{d θ}{d t})}^{2} = 0 \\ \frac{d^{2} x}{d t^{2}} = \frac{m}{m + M} (R - r) (\sin θ {(\frac{d θ}{d t})}^{2} - \cos θ \frac{d^{2} θ}{d t^{2}}) \end{array}$

y en la segunda ecuación del movimiento, sustituimos la aceleración de la cúpula

$\begin{array}{l} \frac{3}{2} {(R - r)}^{2} \frac{d^{2} θ}{d t^{2}} + (R - r) \cos θ \frac{m}{m + M} (R - r) (\sin θ {(\frac{d θ}{d t})}^{2} - \cos θ \frac{d^{2} θ}{d t^{2}}) + g (R - r) \sin θ = 0 \\ \frac{3}{2} (R - r) \frac{d^{2} θ}{d t^{2}} + \cos θ \frac{m}{m + M} (R - r) (\sin θ {(\frac{d θ}{d t})}^{2} - \cos θ \frac{d^{2} θ}{d t^{2}}) + g \sin θ = 0 \\ (\frac{3}{2} - \frac{m}{m + M} \cos^{2} θ) (R - r) \frac{d^{2} θ}{d t^{2}} + \frac{m}{m + M} (R - r) {(\frac{d θ}{d t})}^{2} \cos θ \sin θ + g \sin θ = 0 \\ (\frac{3 M + m + 2 m \sin^{2} θ}{2 (m + M)}) (R - r) \frac{d^{2} θ}{d t^{2}} + \frac{m}{m + M} (R - r) {(\frac{d θ}{d t})}^{2} \cos θ \sin θ + g \sin θ = 0 \\ (\frac{3 M + m + 2 m \sin^{2} θ}{2}) (R - r) \frac{d^{2} θ}{d t^{2}} + m (R - r) {(\frac{d θ}{d t})}^{2} \cos θ \sin θ + (m + M) g \sin θ = 0 \end{array}$

Obteniendo la misma ecuación diferencial que aplicando la Segunda Ley de Newton

Movimiento de los cuerpos

En este apartado describimos el movimiento de la cúpula y la partícula

Movimiento relativo del c. m. del cilindro

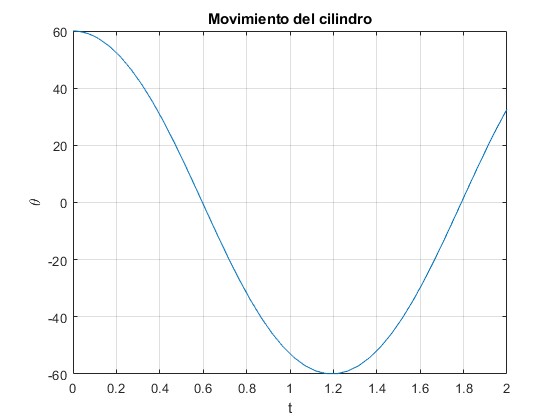
Resolvemos la ecuación diferencial por el procedimiento ode45 de MATLAB para una cúpula de radio R=1 m y un cilindro de radio r=0.125 m. El cociente de m/M=0.2, entre la masa de la partícula y de la cúpula. El c. m. del cilindro parte de la posición θ₀=π/3,

Representamos la posición θ del c. m. del cilindro θ que rueda sin deslizar sobre la cúpula en función del tiempo t

R=1; %radio de la cúpula
r=0.125; %radio del cilindro
m=0.2; %masa partícula
M=1; %masa cúpula
th_0=pi/3; %posición inicial
f=@(t,x) [x(2); -(m*(R-r)*x(2)^2*cos(x(1))*sin(x(1))+(m+M)*9.8*sin(x(1)))
/((R-r)*(3*M+m+2*m*sin(x(1))^2)/2)]; 
[t,x]=ode45(f,[0,2],[th_0,0]);
plot(t,x(:,1)*180/pi)
grid on
xlabel('t')
ylabel('\theta')
title('Movimiento del cilindro')
%energías
E0=m*9.8*(R-r)*(1-cos(th_0)); %inicial
V=-m*(R-r)*x(:,2).*cos(x(:,1))/(m+M); %velocidad cúpula
E=3*m*(R-r)^2*x(:,2).^2/4+m*(R-r)*x(:,2).*V.*cos(x(:,1))+(m+M)*V.^2/2+
m*9.8*(R-r)*(1-cos(x(:,1)));

Comprobamos la conservación de la energía

E0 =
    0.8575
>> E
E =
    0.8575
    0.8575
    ....
    0.8574
    0.8574

Movimiento de la cúpula

No es necesario resolver la ecuación diferencial en x para calcular la posición del centro de la cúpula. En este sistema de dos partículas, el centro de masas permanece fijo, ya que el cilindro y la cúpula parten del reposo

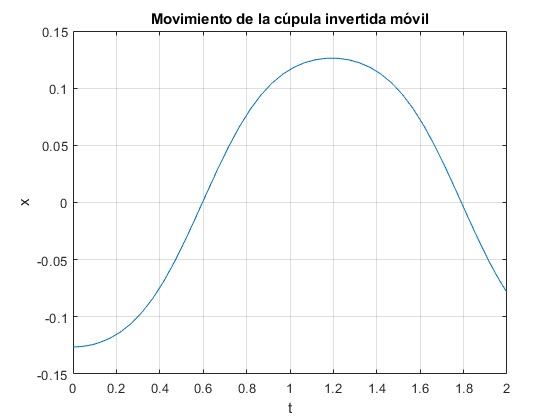
$\begin{array}{l} x_{c m} = \frac{M x + m (x + (R - r) \sin θ)}{m + M} = 0 \\ x = - \frac{m}{m + M} (R - r) \sin θ \end{array}$

Añadimos esta porción de código, para representar la posición del centro de la cúpula x en función del tiempo

...
figure
xx=-m*(R-r)*sin(x(:,1))/(m+M);
plot(t,xx)
grid on
xlabel('t')
ylabel('x')
title('Movimiento de la cúpula invertida móvil')

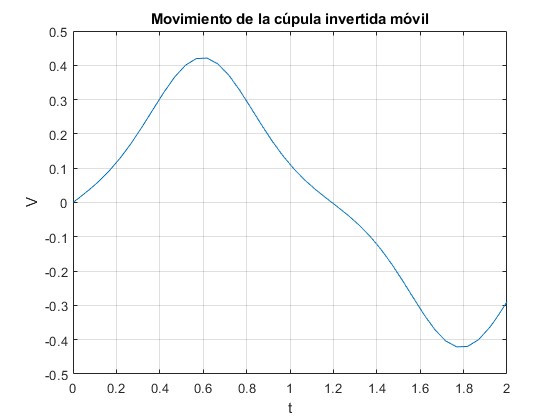
De modo similar, la velocidad de la cúpula es

$V = - \frac{m}{m + M} (R - r) \frac{d θ}{d t} \cos θ$

Añadimos esta porción de código, para representar la velocidad del centro de la cúpula V en función del tiempo

...
figure
plot(t,V)
grid on
xlabel('t')
ylabel('V')
title('Movimiento de la cúpula invertida móvil')

Actividades

Se introduce

El cociente de las masas m/M de la partícula y la masa de la cúpula, en el control titulado Cociente masas
La posición angular inicial de partida de la partícula (en grados) en el control titulado Angulo

Se pulsa el botón titulado Nuevo

En la parte superior, se proporcionan los siguientes datos:

El tiempo t
la posición angular θ del c. m. del cilindro
la velocidad angular dθ/dt del c. m. del cilindro
la energía del sistema que permenece constante
la posición del centro de la cúpula en cm

Cociente masas, m/M:
Angulo:

Referencias

HE Qin，XIE Bing-chuan. The period of vibration of a homogeneous cylinder in a non-fixed inner semicylindrical surface. College Physics Volume 26, Issue 11, 20 November 2007