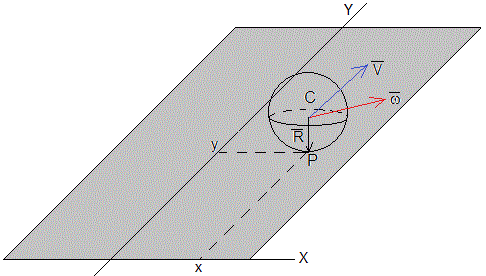
Sea una bola de masa m, radio R y momento de inercia, I_c=2mR²/5. En un instante dado t, el punto de contacto P de la esfera con la pista se encuentra en la posición (x, y). La velocidad del centro de masas es $\overrightarrow{V}$, y la velocidad angular de rotación $\overrightarrow{\omega }$ alrededor de un eje que pasa por el centro de masas.

La velocidad del punto P de contacto de la bola con la pista es

${\displaystyle \begin{array}{l}\begin{array}{l}{\overrightarrow{v}}_p=\overrightarrow{V}+\overrightarrow{\omega }\times \overrightarrow{R}\hfill \\ {\overrightarrow{v}}_p=\left(\begin{array}{c}{V}_x\\ V_y\\ 0\end{array}\right)\left(\begin{array}{ccc}\widehat{i}& \widehat{j}& \widehat{k}\\ {\omega }_x& {\omega }_y& {\omega }_z\\ 0& 0& -R\end{array}\right)=(V_x-R{\omega }_y)\widehat{i}+(V_y+R{\omega }_x)\widehat{j}\hfill \end{array}\\ \{\begin{array}{l}{v}_x=V_x-R{\omega }_y\\ v_y=V_y+R{\omega }_x\end{array}\end{array}}$

Ecuaciones del movimiento

Las fuerzas sobre la bola son:

• El peso, mg
• La reacción de la pista, N
• La fuerza de rozamiento $\overrightarrow{F}$ en el punto de contacto P, cuyo valor y dirección en el plano son desconocidos

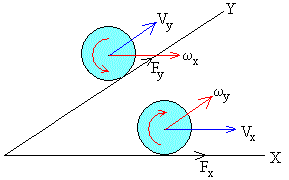
Sean F_x y F_y las componentes de esta fuerza

Las ecuaciones del movimiento son

• Ecuación del movimiento de traslación del centro de masas

${\displaystyle \begin{array}{l}m\frac{d{V}_x}{dt}=F_x\hfill \\ m\frac{d{V}_y}{dt}=F_y\hfill \end{array}}$

• Ecuación del movimiento de rotación alrededor de un eje que pasa por el centro de masas

${\displaystyle \begin{array}{l}{I}_c\frac{d{\omega }_x}{dt}=F_{y}R\hfill \\ I_c\frac{d{\omega }_y}{dt}=-F_{x}R\hfill \end{array}}$

La componente ω_z de la velocidad angular permanece constante

Relacionamos las componentes de la velocidad del centro de masas con las componentes de la velocidad angular de rotación. Teniendo en cuenta que el momento de inercia I_c=2mR²/5.

${\displaystyle \begin{array}{l}R\frac{d{\omega }_x}{dt}=\frac{5}{2}\frac{d{V}_y}{dt}\hfill \\ R\frac{d{\omega }_y}{dt}=-\frac{5}{2}\frac{d{V}_x}{dt}\hfill \end{array}}$

Hemos calculado las componentes de la velocidad del punto P de contacto con la pista, derivando con respecto del tiempo

${\displaystyle \{\begin{array}{l}\frac{d{v}_x}{dt}=\frac{d{V}_x}{dt}-R\frac{d{\omega }_y}{dt}=\frac{7}{2}\frac{d{V}_x}{dt}=\frac{7}{2}\frac{F_x}{m}\\ \frac{d{v}_y}{dt}=\frac{d{V}_y}{dt}+R\frac{d{\omega }_x}{dt}=\frac{7}{2}\frac{d{V}_y}{dt}=\frac{7}{2}\frac{F_y}{m}\end{array}}$

Cuando el punto P desliza sobre la pista, la fuerza de rozamiento es de signo contrario a la velocidad del punto P y vale, $\overrightarrow{F_r}=-\mu N\widehat{v}=-\mu mg\widehat{v}$, siendo μ el coeficiente cinético y $\widehat{v}$ el vector unitario en la dirección de la velocidad del punto de contacto P. Las ecuaciones son

${\displaystyle \{\begin{array}{l}\frac{d{v}_x}{dt}=-\frac{7}{2}\mu g\frac{v_x}{\sqrt{v_x^2+v_y^2}}\\ \frac{d{v}_y}{dt}=-\frac{7}{2}\mu g\frac{v_y}{\sqrt{v_x^2+v_y^2}}\end{array}}$

La ecuación de una línea recta de pendiente m que pasa por el origen es y=mx, dy=m·dx, o bien dy/y=dx/x.

Las componentes de la velocidad del punto de contacto P están relacionadas, v_x=cv_y, donde la constante c se determina a partir de las condiciones iniciales , en el intente t=0, la velocidad del centro de masas es (V_0x, V_0y) y la velocidad angular de rotación (ω_0x, ω_0y)

${\displaystyle c=\frac{v_{0x}}{v_{0y}}=\frac{V_{0x}-R{\omega }_{0y}}{V_{0y}+R{\omega }_{0x}}}$

Integramos la primera ecuación diferencial, sustituyendon v_x=c·v_y

${\displaystyle \begin{array}{l}\frac{d{v}_x}{dt}=-\frac{7}{2}\mu g\frac{c{v}_y}{\sqrt{c^2{v}_y^2+v_y^2}}\\ v_x=v_{0x}-\frac{7}{2}\mu g\frac{c}{\sqrt{c^2+1}}t\end{array}}$

Integramos la segunda ecuación diferencial, de forma similar

${\displaystyle \begin{array}{l}\frac{d{v}_y}{dt}=-\frac{7}{2}\mu g\frac{v_y}{\sqrt{c^2{v}_y^2+v_y^2}}\\ \frac{d{v}_y}{dt}=-\frac{7}{2}\mu g\frac{1}{\sqrt{c^2+1}}\\ v_y=v_{0y}-\frac{7}{2}\mu g\frac{1}{\sqrt{c^2+1}}t\end{array}}$

La velocidad del punto P de contacto se anula cuando v_x y v_y se anulen simultáneamente, en el instante t tal que

${\displaystyle \begin{array}{l}{v}_{0x}=\frac{7}{2}\mu g\frac{c}{\sqrt{c^2+1}}t\\ v_{0y}=\frac{7}{2}\mu g\frac{1}{\sqrt{c^2+1}}t\end{array}}$

Elevando al cuadrado y sumando

${\displaystyle \begin{array}{l}{v}_{0x}^2+v_{0y}^2=\frac{49}{4}{\mu }^2{g}^2\frac{c^2+1}{c^2+1}{t}^2\\ t_c=\frac{2}{7}\frac{v_0}{\mu g}\end{array}}$

A partir de este instante, la bola rueda sin deslizar

Movimiento del centro de masas

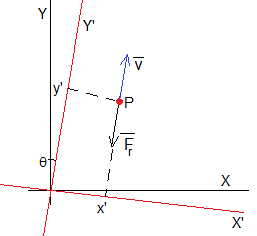
La recta Y' es la dirección constante de la velocidad $\overrightarrow{v}$ del punto P y por tanto, de la fuerza de rozamiento. forma un ángulo c=tanθ con el eje Y

Establecemos un sistema de coordenadas X',Y' giradas un ángulo θ respecto de X,Y , tal como se muestra en la figura. El movimiento del centro de masas de la bola es composición de dos movimientos: uniforme a lo largo del eje X' y uniformemente acelerado a lo largo del eje Y'

${\displaystyle \{\begin{array}{l}{a}_x^{\text{'}}=0\\ a_y^{\text{'}}=-\mu g\end{array}\{\begin{array}{l}{V}_x^{\text{'}}=V_{0x}^{\text{'}}\\ V_y^{\text{'}}=V_{0y}^{\text{'}}-\mu gt\end{array}\{\begin{array}{l}x\text{'}=V_{0x}^{\text{'}}t\\ y\text{'}=V_{0y}^{\text{'}}t-\frac{1}{2}\mu g{t}^2\end{array}}$

La posición y velocidad del centro de masas en el instante t=t_c es

${\displaystyle \{\begin{array}{l}{V}_{cx}^{\text{'}}=V_{0x}^{\text{'}}\\ V_{cy}^{\text{'}}=V_{0y}^{\text{'}}-\mu g{t}_c\end{array}\{\begin{array}{l}{x}_c^{\text{'}}=V_{0x}^{\text{'}}{t}_c\\ y_c^{\text{'}}=V_{0y}^{\text{'}}{t}_c-\frac{1}{2}\mu g{t}_c^2\end{array}}$

A partir de este instante, la bola rueda sin deslizar y el centro de masas se mueve a lo largo de una línea recta con velocidad constante

${\displaystyle \{\begin{array}{l}x\text{'}=x_c^{\text{'}}+V_{cx}^{\text{'}}(t-t_c)\\ y\text{'}=y_c^{\text{'}}+V_{cy}^{\text{'}}(t-t_c)\end{array}}$

Transformación de coordenadas

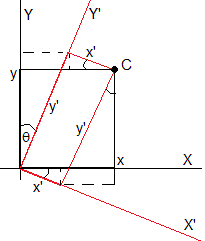
La relación entre la posición (x, y) del centro de masas C de la bola en el Sistema de Referencia X,Y y la misma posición (x', y') en el Sistema de Referencia X',Y' se puede deducir de la figura

${\displaystyle \{\begin{array}{l}x=x\text{'}\cos \theta +y\text{'}\sin \theta \\ y=-x\text{'}\sin \theta +y\text{'}\cos \theta \end{array}}$

Teniendo en cuenta las relaciones trigonométricas

${\displaystyle \cos \theta =\frac{1}{\sqrt{1+{\tan }^2\theta }},\sin \theta =\frac{\tan \theta }{\sqrt{1+{\tan }^2\theta }}}$

Obtenemos las relaciones

${\displaystyle \{\begin{array}{l}x=\frac{1}{\sqrt{c^2+1}}\left(x\text{'}+cy\text{'}\right)\\ y=\frac{1}{\sqrt{c^2+1}}\left(-cx\text{'}+y\text{'}\right)\end{array}}$

Trayectoria

En el instante t=0, la velocidad del centro de masas es (V_0x, V_0y), y la velocidad angular inicial de rotación alrededor de un eje que pasa por el centro de masas es (ω_0x, ω_0y).

Para dibujar la trayectoria de la bola en la pista seguimos estos pasos

Desliza

• La velocidad inicial del punto P de contacto de la esfera con la pista es

${\displaystyle \{\begin{array}{l}{v}_{0x}=V_{0x}-R{\omega }_{0y}\\ v_{0y}=V_{0y}+R{\omega }_{0x}\end{array}}$

Donde c=v_0x/v_0y, señala la dirección constante de la velocidad

• El punto P de contacto de la esfera con la pista desliza durante un tiempo

${\displaystyle t_c=\frac{2}{7}\frac{v_0}{\mu g}}$

A partir de este instante la bola rueda sin deslizar

• La velocidad inicial del centro de masas en el Sistema de Referencia X',Y' es

${\displaystyle \begin{array}{l}\{\begin{array}{l}{V}_{0x}=\frac{1}{\sqrt{c^2+1}}\left(V_{{}_{0x}}^{\text{'}}+c{V}_{{}_{0y}}^{\text{'}}\right)\\ V_{0y}=\frac{1}{\sqrt{c^2+1}}\left(-c{V}_{{}_{0x}}^{\text{'}}+V_{{}_{0y}}^{\text{'}}\right)\end{array}\\ V_{{}_{0x}}^{\text{'}}=\frac{V_{0x}-c{V}_{0y}}{\sqrt{c^2+1}},V_{{}_{0y}}^{\text{'}}=\frac{c{V}_{0x}+V_{0y}}{\sqrt{c^2+1}}\end{array}}$

• La trayectoria del centro de masas de la bola en el Sistema de Referencia X',Y' en el intervalo 0<t<t_c es

${\displaystyle \{\begin{array}{l}x\text{'}=V_{0x}^{\text{'}}t\\ y\text{'}=V_{0y}^{\text{'}}t-\frac{1}{2}\mu g{t}^2\end{array}}$

• Se calcula y representa la trayectoria en el Sistema de Referencia X,Y girado un ángulo θ

Rueda sin deslizar

A partir del instante t_c, el centro de masa de la bola se mueve con a lo largo de una recta con velocidad constante

• La posición y velocidad del centro de masas de la bola en el instante t_c es

${\displaystyle \{\begin{array}{l}{V}_{cx}^{\text{'}}=V_{0x}^{\text{'}}\\ V_{cy}^{\text{'}}=V_{0y}^{\text{'}}-\mu g{t}_c\end{array}\{\begin{array}{l}{x}_c^{\text{'}}=V_{0x}^{\text{'}}{t}_c\\ y_c^{\text{'}}=V_{0y}^{\text{'}}{t}_c-\frac{1}{2}\mu g{t}_c^2\end{array}}$

La trayectoria en el Sistema de Referencia X',Y' es

${\displaystyle \{\begin{array}{l}x\text{'}=x_c^{\text{'}}+V_{cx}^{\text{'}}(t-t_c)\\ y\text{'}=y_c^{\text{'}}+V_{cy}^{\text{'}}(t-t_c)\end{array}}$

• Se calcula y representa la trayectoria en el Sistema de Referencia X,Y girado un ángulo θ

Ejemplo 1

• Radio de la bola, R=10.79 cm
• Coeficiente cinético de rozamiento, entre la bola y la pista, μ=0.09
• Velocidad inicial del centro de masas, V_0x=0, V_0y=5.4864 m/s
• Velocidades angulares iniciales de rotación, ω_0x=0, ω_0y=4 rad/s

function bolera
    V0x=0; %velocidades iniciales
    V0y=18*30.48/100;
    w0x=0;
    w0y=4;
    R=0.354*30.48/100; %radio
    mu=0.09; %coeficiente de rozamiento
    v0x=V0x-R*w0y;
    v0y=V0y+R*w0x;
    c=v0x/v0y; %tangente de th
    tc=2*sqrt(v0x^2+v0y^2)/(7*9.8*mu); %tiempo deslizando

%Desliza
    Vp0x=(V0x-c*V0y)/sqrt(c^2+1);
    Vp0y=(c*V0x+V0y)/sqrt(c^2+1);
    t=linspace(0,tc,50);
    xp=Vp0x*t;
    yp=Vp0y*t-mu*9.8*t.^2/2;
    [x,y]=gira(xp,yp);
    hold on
    plot(x,y)
%Rueda sin deslizar
    Vcx=Vp0x;
    Vcy=Vp0y-mu*9.8*tc;
    xc=Vp0x*tc;
    yc=Vp0y*tc-mu*9.8*tc^2/2;
    t=linspace(tc,2*tc, 50);
    xp=xc+Vcx*(t-tc);
    yp=yc+Vcy*(t-tc);
    [x,y]=gira(xp,yp);
    plot(x,y)
    [x,y]=gira(xc,yc);
    line([x,x],[0,y],'lineStyle','--')
    line([0,x],[y,y],'lineStyle','--')
    hold off
    grid on
    xlabel('x')
    ylabel('y')
    title('Movimiento de la bola')
    
    function [x,y]=gira(xp,yp)
       x=(xp+c*yp)/sqrt(c^2+1); 
       y=(-c*xp+yp)/sqrt(c^2+1); 
    end 
end

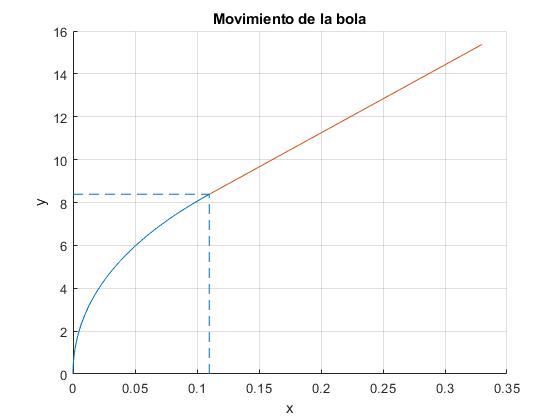
En la figura, se distingue las dos trayectorias que sigue la bola: cuando el punto P de contacto de la bola con la pista desliza y cuando la bola rueda sin deslizar. Se señala la posición de la bola (x_c=0.1099 , y_c=8.3836) m en el instante t_c=1.7828 s

Ejemplo 2

Cambiamos las velocidades iniciales

• Velocidad inicial del centro de masas, V_0x=0.1524, V_0y=5.4864 m/s
• Velocidades angulares iniciales de rotación, ω_0x=4, ω_0y=4 rad/s

En la figura, se distingue las dos trayectorias que sigue la bola: cuando el punto P de contacto de la bola con la pista desliza y cuando la bola rueda sin deslizar. Se señala la posición de la bola (x_c=0.3690, y_c=8.9070) m en el instante t_c=1.9192 s

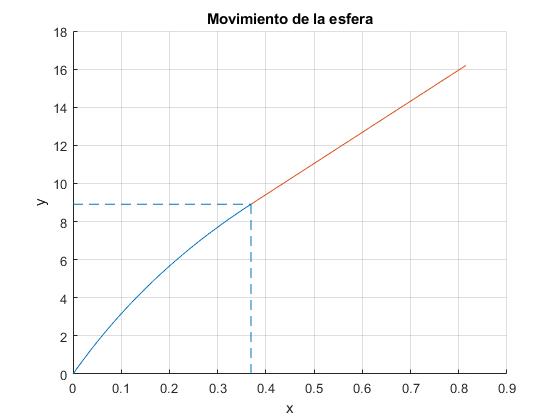
Para que se pueda apreciar la trayectoria, las escalas en el eje X e Y son distintas

Referencias

D. C. Hopkins, J. D. Patterson. Bowling frames: Paths of a bowling ball. Am. J. Phys. 45 (3) March 1977, pp. 263-266