Choques frontales de dos esferas de distinta masa

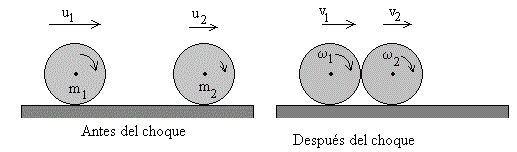
Sean dos esferas de masas m₁ y m₂ que tienen velocidades iniciales u₁ y u₂ antes del choque. Calculamos las velocidades v₁ y v₂ de los c.m. de las esferas después del choque.

1. El principio de conservación del momento lineal

m₁u₁+m₂u₂=m₁v₁+m₂v₂

2. La definición del coeficiente de restitución e.

v₁-v₂₌-e(u₁-u₂)

Despejamos del sistema de dos ecuaciones con dos incógnitas, las velocidades v₁ y v₂ del c.m. de las esferas después del choque

${\displaystyle v_1=\frac{(1-Me)u_1+M(1+e)u_2}{1+M}{v}_2=\frac{(1+e)u_1+(M-e)u_2}{1+M}}$             (1)

donde M=m₂/m₁.

Si suponemos que el rozamiento entre las esferas en el momento en el que entran en contacto es despreciable, las velocidades angulares de rotación no cambian.

ω₁=u₁/r         (2)

Movimiento después del choque

Inmediatamente después del choque no se cumple en general, que las esferas rueden sin deslizar, v_c≠ω·r. Por tanto, como vimos en la página Equilibrio entre el movimiento de traslación y rotación, las fuerzas de rozamiento entre las esferas y el carril sobre el que se mueven restablecerán este equilibrio hasta que se cumpla v_c=ω·r. Más abajo, estudiaremos con detalle ejemplos concretos de los distintos movimientos.

Sean μ₁ y μ₂ o bien μ_i (i=1, 2), los coeficientes cinéticos de rozamiento entre cada una de las esferas y el carril. Puede ocurrir que la velocidad del punto P de contacto de la rueda con el carril sea positiva o negativa

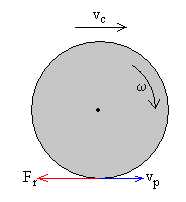
Si v_p=v_c-ω·r>0

La fuerza de rozamiento F_r en P es de signo contrario (hacia la izquierda) tal como se muestra en la figura. F_r=μ_i·N=μ_i·mg.

Las ecuaciones del movimiento de la esfera serán:

• Movimiento de traslación del centro de masas (c.m.)

ma_c=-F_r
a_c=- μ_i g.

Como a_c<0, la velocidad v_c del c.m. disminuye

• Movimiento de rotación alrededor del un eje que pasa por el c.m.

I_cα =F_r·r

${\displaystyle \alpha =\frac{5{\mu }_{i}g}{2r}}$

Como α>0, la velocidad angular de rotación ω aumenta



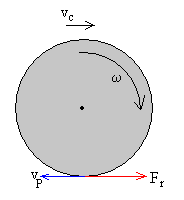
Si v_p=v_c-ω·r<0

La fuerza de rozamiento F_r en P es de signo contrario (hacia la derecha) tal como se muestra en la figura. F_r=μ_i·N=μ_i·mg

Las ecuaciones del movimiento de la esfera serán

• Movimiento de traslación del centro de masas (c.m.)

ma_c=F_r
a_c=μ_i g

Como a_c>0, la velocidad v_c del c.m. aumenta

• Movimiento de rotación alrededor del un eje que pasa por el c.m.

I_cα =-F_r·r

${\displaystyle \alpha =-\frac{5{\mu }_{i}g}{2r}}$

Como α<0, la velocidad angular de rotación ω disminuye

A partir de las ecuaciones de la cinemática del movimiento rectilíneo y circular uniformemente acelerado, calculamos la velocidad del c.m. v_c y la velocidad angular de rotación ω .

v_c=v₀+a_c·t
ω=ω₀+α·t

Movimiento de rodar sin deslizar

En ambos casos v_P<0 y v_P>0, la velocidad del punto P de contacto de la esfera con el carril se anula v_P=0, en el instante t tal que v_c=ω·r, la esfera rueda sin deslizar. La velocidad final del c.m. de la esfera es independiente del coeficiente de rozamiento μ_i (i=1, 2) entre la esfera y el carril.

${\displaystyle v_c=\frac{5v_0+2{\omega }_{0}r}{7}}$

Para cada una de las esferas, los instantes t₁ y t₂ para los cuales empiezan a rodar sin deslizar a partir del momento del choque, son respectivamente.

${\displaystyle t_1=\frac{2\left|v_1-{\omega }_{1}r\right|}{7{\mu }_{1}g}{t}_2=\frac{2\left|v_2-{\omega }_{2}r\right|}{7{\mu }_{2}g}}$

Las velocidades finales constantes V₁ y V₂ de las esferas, a partir de los instantes t₁ y t₂ cuando ruedan sin deslizar son, respectivamente:

${\displaystyle V_1=\frac{5v_1+2{\omega }_{1}r}{7}{V}_2=\frac{5v_2+2{\omega }_{2}r}{7}}$

donde v₁ y v₂ son las velocidades del c.m. de cada una de las esferas justamente después del choque, y ω₁ y ω₂ son las velocidades angulares que adquieren las esferas en dicho instante, fórmulas (1) y (2).

Los coeficientes de rozamiento μ₁ y μ₂ no intervienen en la velocidad final V₁ y V₂ de las esferas. Solamente en el tiempo t₁ y t₂ que tardan en alcanzar estas velocidades.

Ejemplo

• Relación entre las masas de las esferas, M=m₂/m₁=1.0
• Velocidades de las esferas antes del choque, u₁=0.75 y u₂=-0.5.
• Coeficiente de restitución, e=0.72
• Coeficiente de rozamiento entre las esferas y el plano horizontal, μ =0.05.

1. Velocidades v₁ y v₂ de las esferas inmediatamente después del choque, fórmulas (1)

v₁=-0.325
v₂=0.575

2. Velocidades angulares ω₁ y ω₂, no cambian en el choque

rω₁=u₁=0.75
rω₂=u₂=-0.5

3. Movimiento de las esferas después del choque.

• Movimiento de la primera esfera



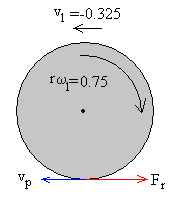
Velocidad del punto P de contacto con el plano horizontal

v_P=v₁-rω₁=-0.325-0.75=-1.075

La fuerza de rozamiento se opone al movimiento de rotación y de traslación, tal como puede verse en la figura

Hasta que se alcanza el equilibrio rotación-traslación  (velocidad final igual a velocidad inicial más aceleración por tiempo)

v₁=-0.325+0.05·9.8·t
rω₁=0.75-5·0.05·9.8·t/2

El instante en el que se cumple que v_P=0, la esfera rueda sin deslizar

v₁=rω₁ por tanto, t₁=0.63 s.

La velocidad final cuando la esfera rueda sin deslizar es

V₁=-0.325+0.05·9.8·t₁=-0.02 m/s

• Movimiento de la segunda esfera



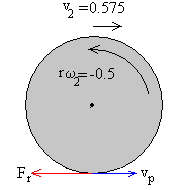
Velocidad del punto P de contacto con el plano horizontal

v_P=v₂-rω₂=0.575+0.5=1.075

La fuerza de rozamiento se opone al movimiento de rotación y de traslación, tal como puede verse en la figura

Hasta que se alcanza el equilibrio rotación-traslación (velocidad final igual a velocidad inicial más aceleración por tiempo)

v₂=0.575-0.05·9.8·t
rω₂=-0.5+5·0.05·9.8·t/2

El instante en el que se cumple que v_P=0, la esfera rueda sin deslizar

v₂=rω₂ por tanto, t₂=0.63 s.

La velocidad final cuando la esfera rueda sin deslizar es

V₂=0.575-0.05·9.8· t₂=0.27 m/s

Actividades

Se introduce

• Las velocidades de las esferas antes del choque, u₁ y u₂ en los controles titulados Velocidad esfera 1 y V. esfera 2, respectivamente
• El coeficiente de restitución e, en el control titulado Coef. restitución
• El cociente M=m₂/m₁ entre las masas de las dos esferas, en el control titulado Cociente masas m₂/m₁
• El coeficiente de rozamiento entre las esferas y el carril se ha fijado en μ₁= μ₂=0.05, para que se pueda ver la transición hacia el equilibrio (rodar sin deslizar) de las esferas. Este coeficiente, no interviene en las velocidades finales
• El radio de las esferas se ha fijado en r=10 cm

Se pulsa el botón titulado Nuevo

Vemos el balance energético de la colisión. La energía antes del choque, (suma de la energía cinética correspondiente al movimiento de traslación del c.m. y de la energía cinética correspondiente al movimiento de rotación alrededor de un eje que pasa por el c.m.) y la energía después del choque en colores más claros.

Se muestra mediante flechas, la velocidad del c.m. de la esfera y la velocidad del punto P de contacto entre la esfera y el carril.

Se sugiere al lector, que estudie los choques elásticos e=1 de dos bolas de billar de la misma masa y radio

Choque de dos esferas iguales que ruedan sobre un carril horizontal

En esta sección, estudiamos el choque elástico y posterior movimiento de dos esferas iguales de radio R a lo largo de un carril acanalado horizontal cuyas vías están separadas una distancia d<2R.

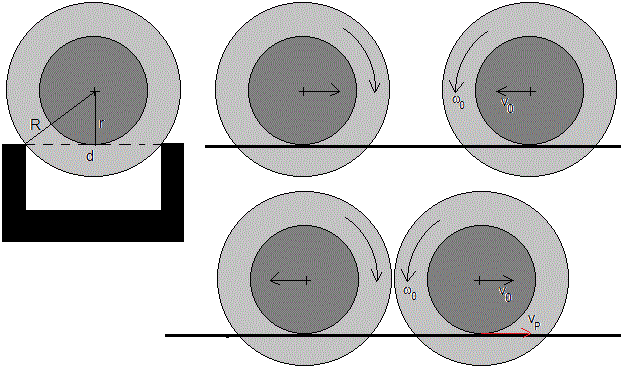
A la izquierda de la figura, se muestra la esfera en el carril acanalado. A la derecha arriba, las esferas antes del choque, ruedan sin deslizar, v_P=v₀-ω₀·r=0, la velocidad del punto de contacto de la esfera derecha (la izquierda, por simetría, es similar) con el carril es nula. Inmediatamente después del choque, las esferas cambian el signo de la velocidad de traslación del c.m. de -v₀ a v₀, quedando la velocidad angular de rotación ω₀ inalterada. Esto hace que la velocidad del punto P de contacto de la rueda con el carril ya no sea nula, sino v_P=v₀+ω₀r=2v₀

La fuerza de rozamiento es de sentido contrario a v_P, disminuyendo esta velocidad hasta que se anule, entonces, la esfera vuelve a rodar sin deslizar, v_P=v₀-ω₀·r=0

La esfera tiene dos puntos de contacto con el carril. Hay por tanto, dos fuerzas de rozamiento F_r y dos reacciones N del carril. La fuerza de rozamiento F_r tiene la dirección del carril, la reacción N es perpendicular al carril y pasa por el centro de la esfera.

• La resultante de las fuerzas de rozamiento es F₁=2F_r
• La resultante de las dos reacciones iguales y simétricas es N₁=2Nr/R, es igual al peso mg

Siendo r la distancia entre el plano que contiene las dos vías del carril y el centro de la esfera r²=R²-d²/4.

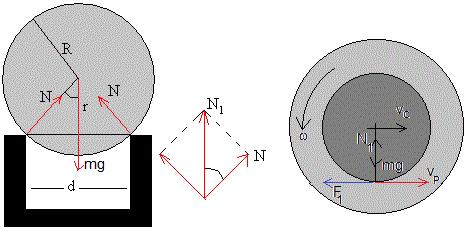
Las fuerzas que actúan sobre la esfera son:

• El peso mg
• La resultante de las reacciones N₁
• La resultante de las fuerzas de rozamiento F₁=2F_r

Las ecuaciones del movimiento de la esfera son

• Equilibrio en la dirección perpendicular al plano inclinado

N₁=mg

• Movimiento de traslación del c.m.

-F₁=ma_c

F₁=2F_r=2μ_kN=μ_kmgR/r

Siendo μ_k el coeficiente cinético de rozamiento

• Movimiento de rotación alrededor de un eje que pasa por el c.m. (Tomando como positivo el sentido de las agujas del reloj)

F₁·r=I_c·α

Teniendo en cuenta que, el momento de inercia de una esfera es I_c=2mR²/5. Despejamos las aceleraciones a_c del centro de masas y α

${\displaystyle a_c=-{\mu }_{k}g\frac{R}{r},\alpha =\frac{5}{2}\frac{{\mu }_{k}g}{R}}$

Tomando el instante t=0, el momento del choque en el origen. La posición y velocidad del centro de masas son

${\displaystyle \begin{array}{l}{v}_c=v_0-{\mu }_{k}g\frac{R}{r}t\\ x_c=R+v_{0}t-\frac{1}{2}{\mu }_{k}g\frac{R}{r}{t}^2\end{array}}$

El ángulo girado y la velocidad angular de rotación son

${\displaystyle \begin{array}{l}\omega =-{\omega }_0+\frac{5}{2}\frac{{\mu }_{k}g}{R}t\\ \theta =-{\omega }_{0}t+\frac{1}{2}\frac{5}{2}\frac{{\mu }_{k}g}{R}{t}^2\end{array}}$

La velocidad del punto P de contacto de la esfera con el carril es

${\displaystyle \begin{array}{l}{v}_p=v_c-\omega r=v_0-{\mu }_{k}g\frac{R}{r}t-\left(-{\omega }_0+\frac{5}{2}\frac{{\mu }_{k}g}{R}t\right)r\\ v_p=2v_0-{\mu }_{k}g\left(\frac{R}{r}+\frac{5}{2}\frac{r}{R}\right)t\end{array}}$

Esta velocidad se hace nula, v_P=0, la esfera rueda sin deslizar a partir del instante t_d

${\displaystyle t_d=\frac{4v_0}{{\mu }_{k}g}\frac{\left(\frac{r}{R}\right)}{2+5{\left(\frac{r}{R}\right)}^2}}$

La posición y velocidad de la esfera en dicho instante t_d son

${\displaystyle \begin{array}{l}{v}_c=v_0\frac{-2+5{\left(\frac{r}{R}\right)}^2}{2+5{\left(\frac{r}{R}\right)}^2}\\ \omega =\frac{v_0}{r}\frac{-2+5{\left(\frac{r}{R}\right)}^2}{2+5{\left(\frac{r}{R}\right)}^2}\\ x=R+\frac{20v_0^2{\left(\frac{r}{R}\right)}^3}{{\mu }_{k}g{\left(2+5{\left(\frac{r}{R}\right)}^2\right)}^2}\end{array}}$

Comprobamos que en dicho instante t_d, la velocidad del punto P de contacto de la esfera con el carril es nula, v_P=v_c-ω·r=0

Ejemplos

• Coeficiente cinético, μ_k=0.2
• Radio de la esfera, R=10 cm=0.1 m
• Velocidad del centro de la esfera, antes del choque, v_c=-0.5 m/s

La velocidad angular inicial de rotación que no cambia, ω₀=v_c/r, con r²=R²-d²/4

La velocidad del centro de la esfera cambia de signo a v₀=0.5 m/s, inmediatamente después del choque

Representamos la velocidad del centro de la esfera v_c, la velocidad angular de rotación ω y la velocidad del punto P de contacto de la esfera con el carril v_P=v_c-ω·r

Ejemplo 1

• Distancia entre las vías, d=R=10 cm=0.1 m

mu=0.2; %coeficiente de rozamiento, cinético
R=0.1; %radio de la esfera
vCM=-0.5; %velocidad inicial antes del choque
hold on
d=R; %distancia entre vías
r=sqrt(R^2-d^2/4); %radio 
v0=-vCM; %cambia de sentido después del choque
w0=vCM/r; %velocidad angular inicial de rotación, la inicial antes del choque
td=4*v0_CM*(r/R)/(mu*9.8*(2+5*(r/R)^2)); %tiempo hasta que rueda sin deslizar
aCM=mu*9.8*R/r; %aceleración del centro de masas
aRot=5*9.8*mu/(2*R); %aceleración angular de rotación
fplot(@(t) (w0+aRot*t)*r,[0,td])
fplot(@(t) v0-aCM*t,[0,td])
fplot(@(t) v0-aCM*t-(w0+aRot*t)*r,[0,td])
legend('\omega·r','v_c','v_p')
hold off
grid on
xlabel('t')
ylabel('v')
title('Velocidades')



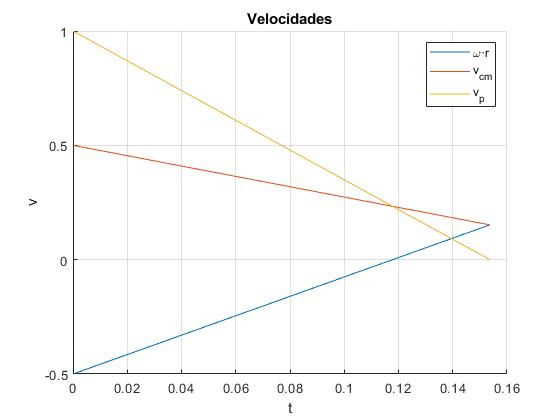
La velocidad angular de rotación ω se anula en el instante

${\displaystyle t=\frac{2v_0}{5{\mu }_{k}g\left(\frac{r}{R}\right)}}$

Ejemplo 2

• Distancia entre las vías, d=1.8R=18 cm=0.18 m

Cambiamos la línea de código,

...
d=1.8*R; %distancia entre vías
...



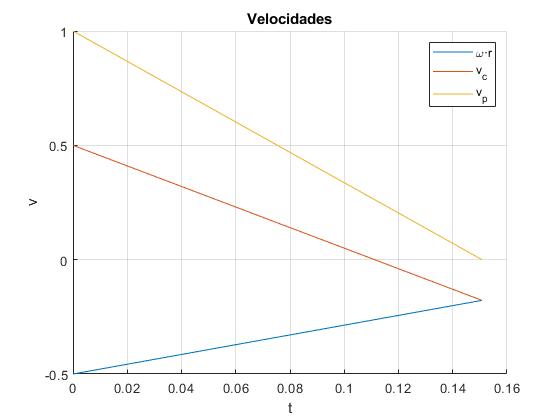
La velocidad del centro de la esfera v_c se anula en el instante

${\displaystyle t=\frac{v_0}{{\mu }_{k}g}\left(\frac{r}{R}\right)}$

Luego, se hace negativa, las esferas regresan al origen y vuelven a chocar, este es el caso más importante.

Ejemplo 3

La velocidad del centro de la esfera v_c y la velocidad angular de rotación ω se anulan simultáneamente para un determinado valor de la separación d entre las vías

${\displaystyle \begin{array}{l}{v}_0-{\mu }_{k}g\frac{R}{r}t=0\\ -{\omega }_0+\frac{5}{2}\frac{{\mu }_{k}g}{R}t=0\end{array}\}r=\sqrt{\frac{2}{5}}R,d=2\sqrt{\frac{3}{5}}R}$

• Distancia entre las vías, $d=2\sqrt{\frac{3}{5}}R$

Cambiamos la línea de código,

...
d=sqrt(12/5)*R; %distancia entre vías
...

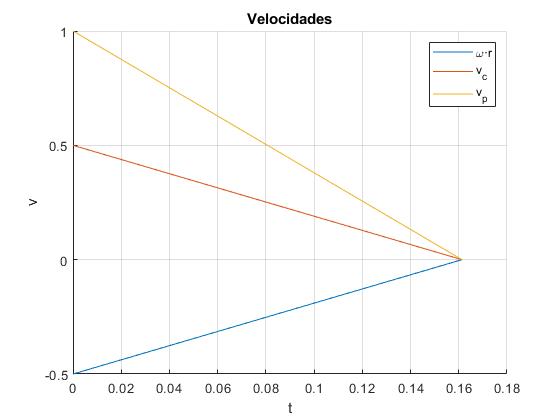
Sucesivos choques

Se producen múltiples choques cuando la distancia entre las vías cumple, $2\sqrt{\frac{3}{5}}R<d<2R$

• Coeficiente cinético, μ_k=0.2
• Radio de la esfera, R=10 cm=0.1 m
• Velocidad del centro de la esfera, antes del choque, v_c=-0.5 m/s
• Distancia entre las vías, d=18 cm=0.18 m

Representamos la velocidad del centro v_c de la esfera en función del tiempo

mu=0.2; %coeficiente de rozamiento, cinético
R=0.1; %radio de la esfera
vCM=-0.5; %velocidad inicial antes del choque
hold on
d=1.8*R; %distancia entre vías
r=sqrt(R^2-d^2/4); %radio 
aCM=mu*9.8*R/r; %aceleración del centro de masas
aRot=5*9.8*mu/(2*R); %aceleración angular de rotación
t0=0;
for i=1:4
    v0=-vCM; %cambia de sentido después del choque
    w0=vCM/r; %velocidad angular inicial de rotación, la inicial antes del choque
    td=4*v0*(r/R)/(mu*9.8*(2+5*(r/R)^2)); %tiempo hasta que rueda sin deslizar
    fplot(@(t) v0-aCM*(t-t0),[t0,t0+td], 'color','r')
    vCM=v0*(-2+5*(r/R)^2)/(2+5*(r/R)^2);
    xf=R+20*v0^2*(r/R)^3/((2+5*(r/R)^2)^2*mu*9.8);
    plot(t0+td,vCM,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
    tf=-(xf-R)/vCM; %tiempo hasta el choque
    line([t0+td, t0+td+tf],[vCM,vCM],'color','b')
    line([t0+td+tf,t0+td+tf],[vCM,-vCM],'color','k','lineStyle','--')
    t0=t0+td+tf;
end
hold off
grid on
xlabel('t')
ylabel('v')
title('Múltiples choques')

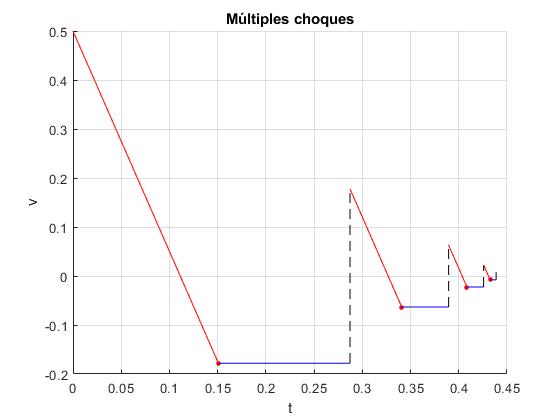
Las distintas etapas del movimiento de la esfera derecha (el movimiento de la esfera izquierda es simétrico) son las siguientes:

1. La esfera derecha se mueve hacia el origen con velocidad v_c=-0.5 m/s, como rueda sin deslizar, la velocidad angular de rotación es ω=v_c/r

2. Choca con la otra esfera, cambia el sentido de su velocidad de traslación, pero no modifica la velocidad angular de rotación. Instante t=0

3. La fuerza de rozamiento hace que ambas velocidades cambien durante un tiempo t_d, hasta que la velocidad del punto P de contacto de la esfera con la vía sea cero. La posición final y la velocidad final de la esfera en dicho instante son

${\displaystyle t_d=\frac{4v_0}{{\mu }_{k}g}\frac{\left(\frac{r}{R}\right)}{2+5{\left(\frac{r}{R}\right)}^2},\{\begin{array}{l}{v}_c=v_0\frac{-2+5{\left(\frac{r}{R}\right)}^2}{2+5{\left(\frac{r}{R}\right)}^2}\\ x=R+\frac{20v_0^2{\left(\frac{r}{R}\right)}^3}{{\mu }_{k}g{\left(2+5{\left(\frac{r}{R}\right)}^2\right)}^2}\end{array}}$

4. Como la velocidad final v_c es negativa, la esfera se dirige hacia el origen, con velocidad constante emplenado un tiempo t_f=(x-R)/v_c, volviendo a chocar en el instante t_d+t_f

5. Se repite un nuevo ciclo. Las líneas verticales a trazos señalan el instante del choque

6. Después de tres choques, la esfera ha disipado casi toda su energía cinética, su velocidad es próxima cero

Actividades

Se introduce

• El coeficiente de rozamiento entre las esferas y el carril en el control titulado Coef. rozamiento
• La separación d entre las vías del carril, en el control titulado Distancia entre vías (cm)
• Las velocidades de las esferas antes del choque, se han fijado en 0.5 m/s
• El radio de las esferas se ha fijado en R=10 cm=0.1 m

Se pulsa el botón titulado Nuevo

Se observa el movimiento de las esferas, antes del choque y después del choque. En la parte superior izquierda, se muestra la posición y velocidad (traslación y rotación) de la esfera derecha (la izquierda es simétrica) y la velocidad del punto P de contacto de la esfera con el carril

En la parte superior derecha, se muestra la energías: suma de la energía cinética de traslación y cinética de rotación. En color negro, la energía disipada como consecuencia del trabajo de la fuerza de rozamiento

${\displaystyle E_t=\frac{1}{2}m{v}_c^2,E_r=\frac{1}{2}\left(\frac{2}{5}m{R}^2\right){\omega }^2}$

Referencias

Del apartado titulado 'Choque de dos esferas iguales que ruedan sobre un carril horizontal'

S Gröber, J Sniatecki. Collision of two balls in a groove: an interplay between translation and rotation. Eur. J. Phys. 41(2020) 035002