Movimiento del cilindro

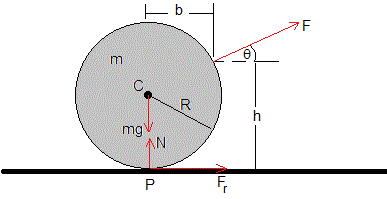
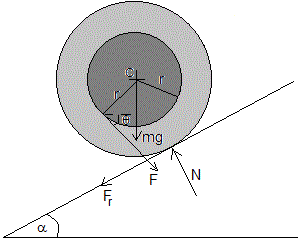
Sea un cilindro de masa m y radio R. Se aplica una fuerza constante F haciendo un ángulo θ (0≤θ<90°) respecto de la horizontal a una cierta altura h, tal como se muestra en la figura.

El cilindro rueda sobre un plano horizontal bajo la acción de la fuerza F y de la fuerza de rozamiento F_r en el punto de contacto P entre el cilindro y el plano horizontal. El sentido de esta fuerza viene determinado por las ecuaciones del movimiento

Supondremos que la componente vertical de la fuerza Fsinθ es menor que el peso mg del cilindro, para que la reacción del plano N=mg-Fsinθ>0.

• La ecuación del movimiento de traslación del centro de masas es

Fcosθ+F_r=ma_c

• La ecuación del movimiento de rotación alrededor del eje del cilindro

${\displaystyle F\cos \theta (h-R)-F\sin \theta b-F_{r}R=\left(\frac{1}{2}m{R}^2\right)\alpha }$

mR²/2 es el momento de inercia del cilindro. La aceleración angular α se considera positiva si tiene el sentido de las agujas del reloj. La distancia b es

${\displaystyle b=\sqrt{R^2-{\left(R-h\right)}^2}=h\sqrt{2\frac{R}{h}-1}}$

Movimiento de rodar sin deslizar

La velocidad del punto P de contacto es nula para que el cilindro ruede sin deslizar. La relación entre aceleraciones es, a_c=αR. En el sistema de dos ecuaciones eliminamos la fuerza de rozamiento F_r

${\displaystyle a_c=\alpha R=\frac{2F}{3m}\left(\frac{h}{R}\cos \theta -\frac{b}{R}\sin \theta \right)}$

Las aceleraciones se anulan para el ángulo crítico θ_c

${\displaystyle \tan {\theta }_c=\frac{h}{b}=\frac{1}{\sqrt{2\frac{R}{h}-1}}}$

Para θ<θ_c, las aceleraciones son positivas. Para θ>θ_c son negativas.

La fuerza de rozamiento F_r no puede ser mayor que la valor máximo μ_sN=μ_s(mg-Fsinθ).

Calculamos la fuerza F que hace que la fuerza de rozamiento alcance su valor máximo. En el sistema de ecuaciones eliminamos la aceleración a_c, y despejamos la fuerza de rozamiento

${\displaystyle \begin{array}{l}\{\begin{array}{l}F\cos \theta +F_r=m{a}_c\\ F\cos \theta \frac{h-R}{R}-F\sin \theta \frac{b}{R}-F_r=\frac{1}{2}m{a}_c\end{array}\\ F_r=F\left(\left(\frac{2}{3}\frac{h}{R}-1\right)\cos \theta -\frac{2}{3}\frac{b}{R}\sin \theta \right)\end{array}}$

Su valor máximo es |F_r|=μ_s(mg-Fsinθ), despejamos F que denominamos F_m

${\displaystyle F_m=\frac{{\mu }_{s}mg}{\left|\left(\frac{2}{3}\frac{h}{R}-1\right)\cos \theta +\left({\mu }_s-\frac{2}{3}\frac{b}{R}\right)\sin \theta \right|}}$

Para que le cilindro ruede sin deslizar la fuerza aplicada F<F_m tendrá que ser menor que la máxima. Por otra parte, la reacción N=mg-Fsinθ>0

Rueda y desliza

La velocidad del punto de contacto P del cilindro con el plano horizontal no es nula. La fuerza de rozamiento es opuesta al sentido de la velocidad v_P. La fuerza de rozamiento vale ahora, |F_r|=μ_k(mg-Fsinθ). Siendo μ_k el coeficiente cinético

Para que el cilindro ruede y deslice la fuerza aplicada F>F_m tiene que ser mayor que la máxima y a su vez, tendrá que cumplir que la reacción N>0, es decir, (mg-Fsinθ)>0. El intervalo de valores de la fuerza aplicada es

${\displaystyle F_m<F<\frac{mg}{\sin \theta }}$

Véamos un ejemplo. Sea μ_s=μ_k=0 y F=mg.

F>F_m=0

La acelearación del centro del cilindro a_c y la aceleración α son

${\displaystyle \begin{array}{l}{a}_c=g\cos \theta \\ \alpha R=2g\left(\left(\frac{h}{R}-1\right)\cos \theta -\frac{b}{R}\sin \theta \right)\end{array}}$

La aceleración del centro de masas a_c>0

La aceleración angular, presenta un comportamiento más complejo. Se anula para el ángulo tanθ_c=(h-R)/b

• Para h<R, la aceleración angular es negativa, α<0

• Para h>R, si θ<θ_c, entonces α>0. Si θ>θ_c, entonces α<0

Ejemplos

Sea el coeficiente estático μ_s=1/4 y el cinético μ_k=1/5

1. La fuerza F se aplica a una altura h/R=2. El ángulo θ=0



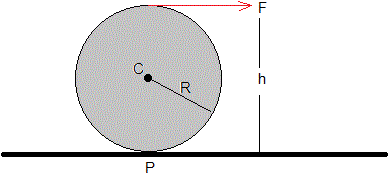
N=mg-Fsinθ=mg>0

La fuerza máxima vale, F_m=3mg/4

Analizamos el comportamiento del cilindro para dos valores de la fuerza aplicada F

• F=mg

En este caso, F>F_m, el cilindro rueda y desliza: a_c=6g/5 y αR=8g/5.

• F=mg/4

En este caso, F<F_m, el cilindro rueda sin deslizar: a_c=αR=g/3.

2. La fuerza F se aplica a una altura h/R=1. El ángulo θ=90°



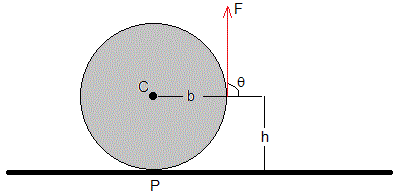
Como vemos en la figura, b/R=1

La fuerza máxima vale, F_m=3mg/5

Analizamos el comportamiento del cilindro para dos valores de la fuerza aplicada F

• F=mg

N=mg-Fsinθ=0. No hay fuerza de rozamiento

En este caso, F>F_m, el cilindro rueda y desliza: a_c=0 y αR=-2g.

• F=mg/4

N=mg-Fsinθ>0.

En este caso, F<F_m, el cilindro rueda sin deslizar: a_c=αR=-g/6.

3. La fuerza F se aplica a una altura h/R=1/2. El ángulo θ=60°



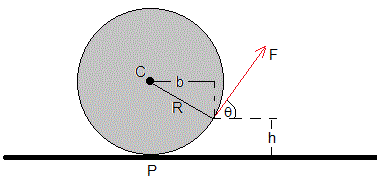
La distancia $\frac{b}{R}=\frac{\sqrt{3}}{2}$

La fuerza máxima vale,

${\displaystyle F_m=\frac{mg}{\left|\frac{\sqrt{3}}{2}-\frac{10}{3}\right|}=0.4053·mg}$

Analizamos el comportamiento del cilindro para dos valores de la fuerza aplicada F

• F=mg

N=mg-Fsinθ>0.

En este caso, F>F_m, el cilindro rueda y desliza:

${\displaystyle a_c=\frac{g}{10}\left(7-\sqrt{3}\right),\alpha R=\left(\frac{\sqrt{3}}{5}-\frac{12}{5}\right)g}$

• F=mg/4

N=mg-Fsinθ>0.

En este caso, F<F_m, el cilindro rueda sin deslizar: a_c=αR=-g/12.

Movimiento del carrete

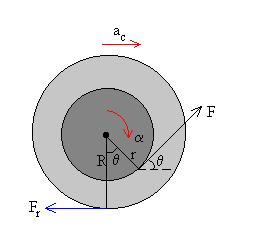
Aplicamos una fuerza F al carrete haciendo un ángulo θ con la horizontal tal como se indica en la figura. La fuerza F tiene una componente horizontal F·cosθ .

Las ecuaciones del movimiento son ahora.

• Equilibrio en la dirección vertical

N+F·sinθ=mg

Siendo N la reacción del plano horizontal. Supondremos N≥0, para que el carrete esté siempre en contacto con la superficie horizontal.

• Ecuación de la dinámica de la traslación del c.m.

F·cosθ-F_r=m·a_c

• Ecuación de la dinámica de rotación alrededor de un eje que pasa por el c.m.

-F·r+F_r·R=I_c·α

Donde I_c es el momento de inercia del carrete respecto de un eje que pasa por su eje central

Si se cumple que |F_r|≤μ_s·N y además, el carrete rueda sin deslizar a_c=α·R, despejamos la aceleración del centro de masas a_c y la fuerza de rozamiento F_r.

${\displaystyle a{}_c=\frac{F}{mk}\left(\cos \theta -\frac{r}{R}\right)k=1+\frac{I_c}{m{R}^2}}$

${\displaystyle F_r=\frac{F}{k}\left(\frac{I_c}{m{R}^2}\cos \theta +\frac{r}{R}\right)}$

Consecuencias

1. La aceleración del c.m. a_c es nula para cosθ=r/R

Para estos dos ángulos críticos la aceleración del c.m. cambia de signo

${\displaystyle {\theta }_{c1}=\arccos \left(\frac{r}{R}\right){\theta }_{c2}=2\pi -\arccos \left(\frac{r}{R}\right)}$

r_R=0.5; %cociente r/R
fplot(@(x) cos(x)-r_R,[0,2*pi]) %proporcional a la aceleración del c.m.
x1=acos(r_R);
line([x1,x1],[-1.5,0],'lineStyle','--')
x2=2*pi-x1;
line([x2,x2],[-1.5,0],'lineStyle','--')
grid on
xlabel('\theta')
ylabel('a_c')
title('Aceleración')



• Cuando cosθ>r/R, la aceleración a_c es positiva y el carrete se mueve hacia la derecha.

• Cuando cosθ<r/R, la aceleración a_c es negativa y el carrete se mueve hacia la izquierda.

2. La fuerza de rozamiento F_r se anula cuando cosθ_r=-mrR/I_c

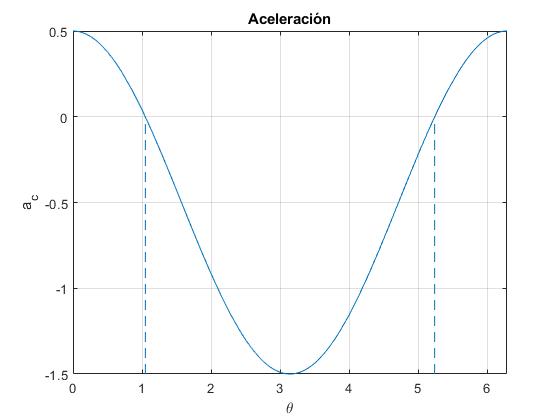
Existen dos ángulos para los cuales la fuerza de rozamiento cambia de signo, siempre que se cumpla que I_c>mrR

${\displaystyle {\theta }_{r1}=\arccos \left(-\frac{mrR}{I_c}\right){\theta }_{r2}=2\pi -\arccos \left(-\frac{mrR}{I_c}\right)}$

Condición de rodar sin deslizar

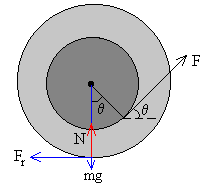
Queda por determinar el intervalo de ángulos θ para cada fuerza F, para los cuales se cumple que el valor absoluto de la fuerza de rozamiento F_r no exceda el valor máximo μ_s·N

${\displaystyle \left|\frac{F}{k}\left(\frac{I_c}{m{R}^2}\cos \theta +\frac{r}{R}\right)\right|\le {\mu }_s\left(mg-F\sin \theta \right)}$

El valor máximo de F es

${\displaystyle F_m=\frac{{\mu }_{s}mg}{\frac{I_c}{m{R}^2}\cos \theta +\frac{r}{R}+k{\mu }_s\sin \theta }}$

Cuando rueda y desliza

Cuando el valor absoluto de la fuerza de rozamiento alcanza su valor máximo |F_r|=μ_s·N, el carrete empieza a rodar deslizando, se deja de cumplir la relación entre las dos aceleraciones a_c≠α·R

• la ecuación de la dinámica de traslación del c.m. nos da el valor de la aceleración a_c con F_r=μ_k·N
• la ecuación de la dinámica de rotación alrededor de un eje que pasa por el c.m. nos da el valor de la aceleración angular α

Carrete de forma cilíndrica

Consideremos un carrete de forma cilíndrica de masa m y radio R, con una pequeña hendidura de radio r, donde se enrolla la cuerda de cuyo extremo se tira con una fuerza F haciendo una ángulo θ con la horizontal. Se supone que la hendidura no contribuye a la masa m o al momento de inercia I_c=mR²/2 del cilindro.

${\displaystyle a_c=\frac{2F}{3m}\left(\cos \theta -\frac{r}{R}\right)F_r=\frac{F}{3}\left(\cos \theta +2\frac{r}{R}\right)}$

El máximo valor de la fuerza de rozamiento vale, μ_s(mg-Fsinθ)

• La aceleración a_c se anula para cosθ=r/R
• La fuerza de rozamiento F_r se anula para un valor del ángulo θ_r tal que

${\displaystyle \cos \theta =-\frac{2r}{R}}$

Ejemplo:

Sea la masa del carrete m=1 kg, cociente r/R=0.3 y μ=0.6

1. Si θ=30º, tirando con una fuerza F>2g el carrete deja de tener contacto con el suelo

2. θ_c=72.5º, la aceleración a_c=0. Para θ<θ_c, el carrete se mueve hacia la derecha, para θ>θ_c, el carrete se mueve hacia la izquierda

3. θ_r=126.8º la fuerza de rozamiento se hace cero

Dado el valor de la fuerza F, el cociente r/R y el coeficiente μ, vamos a investigar los ángulos 0<θ<π para los que se cumple que |F_r|≤μ_s·N

Representamos las funciones:

${\displaystyle \begin{array}{l}\left|\frac{F}{3}\left(\cos \theta +2\frac{r}{R}\right)\right|\\ {\mu }_s\left(mg-F\sin \theta \right)\end{array}}$

F=5;  %fuerza aplicada 
r_R=0.3; %cociente de radios r/R
mu=0.6;  %coeficiente estático
fr=@(x) abs(F*(cos(x)+2*r_R)/3);
fMax=@(x) mu*(9.8-F*sin(x));
hold on
fplot(fr,[0,pi],'r')
fplot(fMax,[0,pi],'b')
set(gca,'XTick',0:pi/6:pi)
set(gca,'XTickLabel',{'0','\pi/6','\pi/3','\pi/2','2\pi/3','5\pi/6','\pi'})
hold off
grid on
legend('F_r','F_r máx')
xlabel('\theta')
ylabel('F_r')
title('Carrete  que rueda')

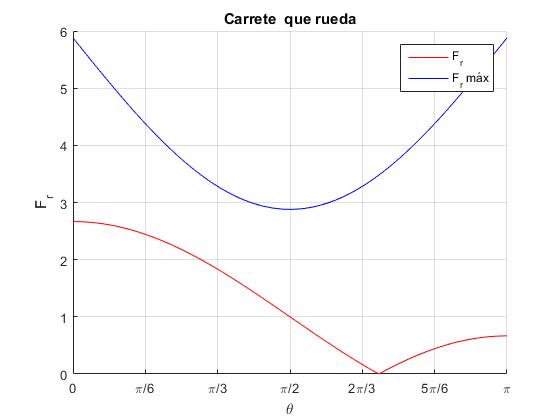
• Para μ=0.6, la fuerza de rozamiento F_r se mantiene inferior al valor máximo μ_sN para todos los ángulos 0<θ<π

• Para μ=0.2, la fuerza de rozamiento F_r alcanza un valor superior al máximo μ_sN para varios ángulos 0<θ<θ_m

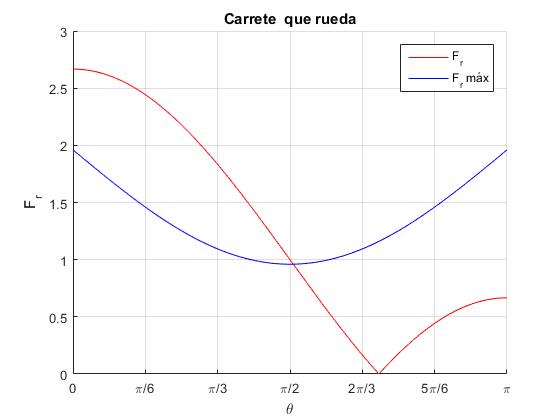
Calculamos el ángulo de intersección θ_m con la función fzero de MATLAB

>> f=@(x) fr(x)-fMax(x);
>> fzero(f,pi/2)*180/pi
ans =   91.3655

Actividades

Se introduce

• El valor de la fuerza aplicada F, en el control titulado Fuerza
• La dirección de dicha fuerza, el ángulo θ, en el control titulado Ángulo
• La relación entre el radio del tambor r en el que está enrollada la cuerda y el radio del carrete R, en el control titulado Cociente r/R.
• El coeficiente estático μ_s, en el control titulado Rozamiento
• La masa está fijada en el programa interactivo m=1 kg

Se pulsa el botón titulado Nuevo

En la parte superior se proporcionan los datos d ela aceleración del centro de masa a_c y de la acleración angular α de rotación alrededor de un eje perpendicular al plano del carrete y que pasa por el c.m. Ambas aceleraciones son iguales si el carrete rueda sin deslizar: a_c= α·R. El radio R=1 del carrete

Se proporciona el valor de la fuerza de rozamiento F_r y del máximo valor de la fuerza de rozamiento μN

Equilibrio. Estática

Plano horizontal

Cuando el carrete descansa sobre el plano horizontal hay dos posibles ángulos de equilibrio θ_c y -θ_c

• Cuando se cumple que θ_c=arccos(r/R).



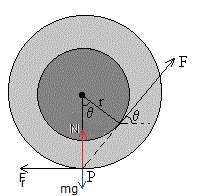
La aceleración del centro de masas a_c es cero. A éste ángulo θ_c se denomina ángulo crítico

La ecuación de equilibrio

${\displaystyle \[ \begin{array}{l}F\cos {\theta }_c=F_r\\ N+F\sin {\theta }_c=mg\end{array}\}{F}_r\le {\mu }_{s}N \]}$

La fuerza de rozamiento F_r ha de ser menor que la máxima μ_sN, por lo que la fuerza aplicada F ha de cumplir

${\displaystyle \begin{array}{l}F\le {\mu }_s\frac{mg}{\cos {\theta }_c+{\mu }_s\sin {\theta }_c}\\ F\le {\mu }_s\frac{mg}{\frac{r}{R}+{\mu }_s\sqrt{1-{\left(\frac{r}{R}\right)}^2}}\end{array}}$

Por otra parte, N=mg-Fsinθ_c>0

${\displaystyle F<\frac{mg}{\sin {\theta }_c}}$

• Cuando se cumple que θ_c=-arccos(r/R). La aceleración del c. m. es cero.



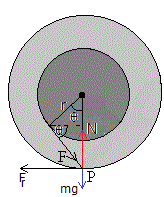
En este caso, las ecuaciones de equilibrio son

${\displaystyle \begin{array}{l}F\cos {\theta }_c=F_r\\ N=mg+F\sin {\theta }_c\end{array}\}{F}_r\le {\mu }_{s}N}$

La fuerza de rozamiento F_r ha de ser menor que la máxima μ_sN, por lo que la fuerza aplicada F ha de cumplir

${\displaystyle \begin{array}{l}F\le {\mu }_s\frac{mg}{\cos {\theta }_c-{\mu }_s\sin {\theta }_c}\\ F\le {\mu }_s\frac{mg}{\frac{r}{R}-{\mu }_s\sqrt{1-{\left(\frac{r}{R}\right)}^2}}\end{array}}$

Se cumple siempre que N>0

Plano inclinado

Supongamos que el carrete descansa sobre un plano inclinado un ángulo α

• Angulo θ positivo



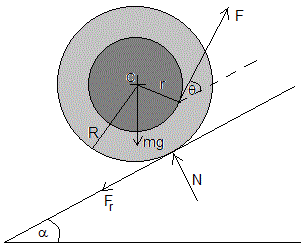
Escribimos las ecuaciones de equilibrio tomando momentos respecto del centro C.

${\displaystyle \theta >0\{\begin{array}{l}F\cos \theta =F_r+mg\sin \alpha \\ N=mg\cos \alpha -F\sin \theta \\ Fr-F_{r}R=0\end{array}}$

Despejamos las incógnitas

${\displaystyle \begin{array}{l}F=mg\frac{\sin \alpha }{\cos \theta -\frac{r}{R}}\\ F_r=\frac{r}{R}F=mg\frac{\frac{r}{R}\sin \alpha }{\cos \theta -\frac{r}{R}}\end{array}}$

${\displaystyle N=mg\left(\cos \alpha -\frac{\sin \alpha }{\cos \theta -\frac{r}{R}}\sin \theta \right)}$

Como r/R<1, se alcanza el equilibrio si cosθ>r/R. Por otra parte, la fuerza de rozamiento tiene que ser menor que su valor máximo, F_r≤μ_sN y la reacción del plano inclinado N>0. Estas condiciones se escriben

${\displaystyle \begin{array}{l}\{\begin{array}{l}0\le \theta <{\theta }_0\\ \cos (\theta +\alpha )>\frac{r}{R}\cos \alpha \\ \cos (\theta +\alpha )\ge \frac{r}{R}\frac{\sin \alpha }{{\mu }_s}+\frac{r}{R}\cos \alpha \end{array}\\ \{\begin{array}{l}0\le \theta <{\theta }_0\\ \cos (\theta +\alpha )\ge \frac{r}{R}\frac{\sin \alpha }{{\mu }_s}+\frac{r}{R}\cos \alpha \end{array}\\ 0\le \theta \le {\theta }_1-\alpha ,\cos {\theta }_1=\frac{r}{R}\frac{\sin \alpha }{{\mu }_s}+\frac{r}{R}\cos \alpha \end{array}}$

• Angulo θ negativo



Escribimos las ecuaciones de equilibrio tomando momentos respecto del centro C.

${\displaystyle \theta <0\{\begin{array}{l}F\cos \theta =F_r+mg\sin \alpha \\ N=mg\cos \alpha -F\sin \theta \\ Fr-F_{r}R=0\end{array}}$

Despejamos las incógnitas

${\displaystyle \begin{array}{l}F=mg\frac{\sin \alpha }{\cos \theta -\frac{r}{R}}\\ F_r=\frac{r}{R}F=mg\frac{\frac{r}{R}\sin \alpha }{\cos \theta -\frac{r}{R}}\end{array}}$

${\displaystyle N=mg\left(\cos \alpha -\frac{\sin \alpha }{\cos \theta -\frac{r}{R}}\sin \theta \right)}$

Obtenemos las mismas ecuaciones

Fijados r/R y μ_s, representamos los valores positivos de la función f(α)

${\displaystyle f\left(\alpha \right)=\arccos \left(\frac{r}{R}\frac{\sin \alpha }{{\mu }_s}+\frac{r}{R}\cos \alpha \right)-\alpha }$

entre 0 y θ₁-α. Para ello, evitamos try...catch que el argumento del arco coseno sea mayor que la unidad y calculamos la raíz (cero) de dicha función.

Por ejemplo, sea r/R=0.4, y μ_s=0.3, para una pendiente de α=pi/12 (15°), los ángulos de equilibrio están comprendidos en el intervalo -0.4885≤θ≤0.4885, (línea vertical)

r=0.4; %cociente r/R
mu=0.3; %coeficiente estático
th_1=@(x) acos(r*sin(x)/mu+r*cos(x))-x;
try
    f=@(x) sin(x)/mu+cos(x)-1/r;
    raiz=fzero(f,[0,pi/2]);
catch
    raiz=pi/2;
end
ang_max=fzero(th_1,[0,raiz]);
hold on
fplot(th_1,[0,ang_max])
fplot(@(x) -th_1(x),[0,ang_max])
th=pi/12;
th_max=th_1(th);
line([th,th],[th_max,-th_max],'color','k')
plot(th,th_max,'ro','markersize',3,'markerfacecolor','r')
plot(th,-th_max,'ro','markersize',3,'markerfacecolor','r')
hold off
grid on
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3', '5\pi/12', '\pi/2'})
set(gca,'YTick',-pi/2:pi/12:pi/2)
set(gca,'YTickLabel',{'-\pi/2','-5\pi/12','-\pi/3','-\pi/4','-\pi/6', 
'-\pi/12','0','\pi/12','\pi/6','\pi/4','\pi/3', '5\pi/12', '\pi/2'})
xlabel('\alpha')
ylabel('\theta')
title('Intervalo angular')

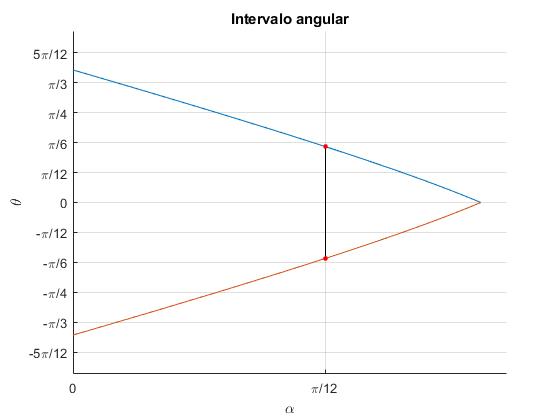
Calculamos la fuerza aplicada F, la fuerza de rozamiento F_r y su valor máximo μ_sN para tres ángulos θ

En los tres casos se cumple que F_r≤μ_sN

Referencias

V Oliveira. Angular and linear accelerations of a rolling cylinder acted by an external force. Eur. J. Phys. 32 (2011) 381-388

Clemens Wagner, Andreas Vaterlaus. Non-slipping domains of a pulled spool. Eur. J. Phys. 35 (2014) 065002

R De Luca, O Faella. Static properties of a spool on an incline: an IBSE lecture proposal. Phys. Educ. 57 (2022) 055002