Momento de inercia

El momento de inercia de un cilindro de base elíptica de semiejes a y b es igual al momento de inercia de una placa de forma elíptica de las mismas dimensiones respecto de un eje perpendicular a la placa y que pase por su centro.

${\displaystyle I_c={\displaystyle \iint r^{2}dm}}$

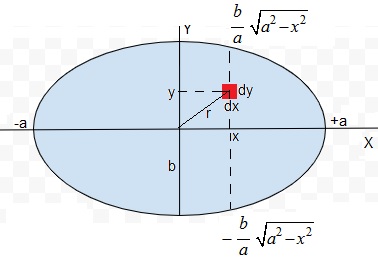
Tomamos un elemento diferencial de área dx·dy, que dista r del eje de rotación, r²=x²+y². La masa dm contenida en este elemento diferencial es

${\displaystyle dm=\frac{m}{\pi ab}dx·dy}$

siendo πab el área de la elipse y m la masa de la placa.

La ecuación de una elipse es

${\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$

Fijado x, los límites de y son

${\displaystyle y=\pm \frac{b}{a}\sqrt{a^2-x^2}}$

Los límites de x son ±a. La integral doble se escribe

${\displaystyle I_c=\frac{m}{\pi ab}{\displaystyle \underset{-a}{\overset{a}{\int }}{\displaystyle \underset{-\frac{b}{a}\sqrt{a^2-x^2}}{\overset{\frac{b}{a}\sqrt{a^2-x^2}}{\int }}\left(x^2+y^2\right)dx·dy}}}$

Integramos respecto de la variable y

${\displaystyle I_c=\frac{m}{\pi ab}{\displaystyle \underset{-a}{\overset{a}{\int }}\left({x^{2}y+\frac{y^3}{3}|}_{-\frac{b}{a}\sqrt{a^2-x^2}}^{\frac{b}{a}\sqrt{a^2-x^2}}\right)dx=}\frac{2m}{\pi ab}\left\{\frac{b}{a}{\displaystyle \underset{-a}{\overset{a}{\int }}{x}^2\sqrt{a^2-x^2}dx+\frac{1}{3}\frac{b^3}{a^3}{\displaystyle \underset{-a}{\overset{a}{\int }}{\left(a^2-x^2\right)}^{3/2}dx}}\right\}}$

Hacemos el cambio de variable, x=asint, dx=acost·dt

${\displaystyle \begin{array}{l}{I}_c=\frac{2m}{\pi a^2}\left\{a^4{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}{\sin }^{2}t·{\cos }^{2}t·dt+\frac{1}{3}\frac{b^2}{a^2}{a}^4{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}{\cos }^{4}t·dt}}\right\}=\\ \frac{2m}{\pi }{a}^2\left\{\frac{1}{4}{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}{\sin }^2\left(2t\right)·dt+\frac{1}{3}\frac{b^2}{a^2}\left({{\cos }^{3}t·\sin t|}_{-\pi /2}^{\pi /2}+3{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}{\sin }^{2}t·{\cos }^{2}t·dt}\right)}\right\}=\\ \frac{2m}{\pi }{a}^2\left\{\frac{1}{8}{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}\left(1-\cos (4t)\right)·dt+\frac{1}{3}\frac{b^2}{a^2}\left(\frac{3}{8}{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}\left(1-\cos (4t)\right)·dt}\right)}\right\}=\\ \frac{m}{4\pi }{a}^2\left\{{\left(t-\frac{1}{4}\sin (4t)\right)|}_{-\pi /2}^{\pi /2}+\frac{b^2}{a^2}{\left(t-\frac{1}{4}\sin (4t)\right)|}_{-\pi /2}^{\pi /2}\right\}\\ I_c=\frac{1}{4}m\left(a^2+b^2\right)\end{array}}$

Cuando a=b, obtenemos el momento de inercia de un disco de radio a respecto de un eje perpendicular al plano del disco y que pasa por su centro

Movimiento de rodar sin deslizar sobre un plano horizontal

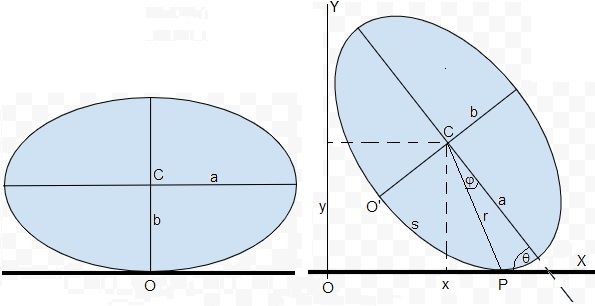
Sea un cilindro de base elíptica de masa m y semiejes a y b, está inicialmente en reposo sobre el plano horizontal tal como se muestra en la figura de la izquierda. La longitud del cilindro l no interviene en la descripción del movimiento

Se hace rodar el cilindro hacia la derecha, P es el punto de contacto entre la elipse y el plano horizontal. La distancia entre O y P es la longitud del arco de elipse entre O' y P. La elipse ha girado un ángulo θ, la intersección del eje mayor de la elipse y el plano horizontal forman un ángulo θ.

Las coordenadas (x, y) del centro de masa se calculan a partir del triángulo rectángulo cuya hipotenusa es r y ángulo en P, θ+φ.

x=s-r·cos(θ+φ)
y=r·sin(θ+φ)

Para describir el movimiento del cilindro de base elíptica, es necesario expresar todas las magnitudes cinemáticas en función del ángulo girado θ

• Tangente a la elipse en el punto P de contacto



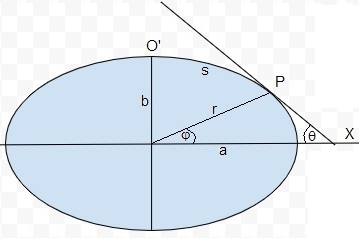
El plano horizontal es tangente a la elipse en P, tal como se muestra en la figura de la elipse girada

Las ecuaciones paramétricas de una elipse son

${\displaystyle \begin{array}{l}\begin{array}{l}x=a\sin \beta \\ y=b\cos \beta \end{array}\}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\\ \tan \phi =\frac{y}{x}=\frac{b}{a\tan \beta }\end{array}}$

El ángulo de la tangente a la elipse en el punto P es π-θ

${\displaystyle \begin{array}{l}\tan \left(\pi -\theta \right)=\frac{dy}{dx}=\frac{\frac{dy}{d\beta }}{\frac{dx}{d\beta }}=\frac{-b\sin \beta }{a\cos \beta }=-\frac{b}{a}\tan \beta \\ \tan \theta =\frac{b}{a}\tan \beta \end{array}}$

• Arco de elipse



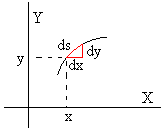
La longitud ds de un elemento diferencial de arco es

${\displaystyle \begin{array}{l}ds=\sqrt{d{x}^2+d{y}^2}=\sqrt{a^2{\cos }^2\beta +b^2{\sin }^2\beta }·d\beta =\\ a\sqrt{1-\frac{a^2-b^2}{a^2}{\sin }^2\beta }·d\beta \end{array}}$

Expresamos el arco ds en términos del ángulo girado θ, utilizando las relaciones trigonométricas

${\displaystyle {\sin }^2\beta =\frac{{\tan }^2\beta }{1+{\tan }^2\beta },{\cos }^2\beta =\frac{1}{1+{\tan }^2\beta }}$

Expresamos sin²β y dβ en términos de θ y dθ

${\displaystyle \begin{array}{l}\tan \beta =\frac{a}{b}\tan \theta \\ \frac{1}{{\cos }^2\beta }d\beta =\frac{a}{b}\frac{1}{{\cos }^2\theta }d\theta \\ d\beta =\frac{ab}{a^2{\sin }^2\theta +b^2{\cos }^2\theta }d\theta \\ ds=\frac{a^2{b}^2}{{\left(a^2{\sin }^2\theta +b^2{\cos }^2\theta \right)}^{3/2}}d\theta \end{array}}$

• Distancia r del centro C de la elipse al punto P de contacto

${\displaystyle r^2=x^2+y^2=a^2{\sin }^2\beta +b^2{\cos }^2\beta =\frac{a^4{\sin }^2\theta +b^4{\cos }^2\theta }{a^2{\sin }^2\theta +b^2{\cos }^2\theta }}$

• Angulo θ+φ del vértice P del triángulo rectángulo.

Expresamos cos(θ+φ) y sin(θ+φ) en términos del ángulo girado θ, partiendo de la relación

${\displaystyle \tan \phi =\frac{b}{a}\tan \beta =\frac{b^2}{a^2}\frac{1}{\tan \theta }}$

Empezamos con el coseno

${\displaystyle \cos \left(\theta +\phi \right)=\cos \left(\theta +\arctan \left(\frac{b^2}{a^2}\frac{1}{\tan \theta }\right)\right)=\cos \theta ·\cos \left(\arctan \left(\frac{b^2}{a^2}\frac{1}{\tan \theta }\right)\right)-\sin \theta ·\sin \left(\arctan \left(\frac{b^2}{a^2}\frac{1}{\tan \theta }\right)\right)}$

Utilizando las relaciones trigonométricas antes mencionadas

${\displaystyle \cos \left(\theta +\phi \right)=\left(a^2-b^2\right)\frac{\sin \theta \cos \theta }{\sqrt{a^4{\sin }^2\theta +b^4{\cos }^2\theta }}}$

Continuamos con el seno

${\displaystyle \begin{array}{l}\sin \left(\theta +\phi \right)=\sin \left(\theta +\arctan \left(\frac{b^2}{a^2}\frac{1}{\tan \theta }\right)\right)=\sin \theta ·\cos \left(\arctan \left(\frac{b^2}{a^2}\frac{1}{\tan \theta }\right)\right)+\cos \theta ·\sin \left(\arctan \left(\frac{b^2}{a^2}\frac{1}{\tan \theta }\right)\right)\\ =\frac{a^2{\sin }^2\theta +b^2{\cos }^2\theta }{\sqrt{a^4{\sin }^2\theta +b^4{\cos }^2\theta }}\end{array}}$

Ya tenemos todos los elementos necesarios para expresar en términos del ángulo girado θ las magnitudes cinemáticas que precisamos.

• La altura y del centro C

${\displaystyle y=r\sin \left(\theta +\phi \right)=\sqrt{a^2{\sin }^2\theta +b^2{\cos }^2\theta }}$

• La componente vertical dy/dt de la velocidad del centro de masas C

${\displaystyle \frac{dy}{dt}=\left(a^2-b^2\right)\frac{\sin \theta \cos \theta }{\sqrt{a^2{\sin }^2\theta +b^2{\cos }^2\theta }}\frac{d\theta }{dt}}$

• La componente horizontal del la velocidad dx/dt del centro de masas C

${\displaystyle \begin{array}{l}x=s-r\cos \left(\theta +\phi \right)=s-\left(a^2-b^2\right)\frac{\sin \theta \cos \theta }{\sqrt{a^2{\sin }^2\theta +b^2{\cos }^2\theta }}\\ \frac{dx}{dt}=\frac{ds}{dt}-\left(a^2-b^2\right)\frac{d}{dt}\frac{\sin \theta \cos \theta }{\sqrt{a^2{\sin }^2\theta +b^2{\cos }^2\theta }}\\ \frac{dx}{dt}=\frac{a^2{b}^2}{{\left(a^2{\sin }^2\theta +b^2{\cos }^2\theta \right)}^{3/2}}\frac{d\theta }{dt}-\frac{\left(a^2-b^2\right)\left(b^2{\cos }^4\theta -a^2{\sin }^4\theta \right)}{{\left(a^2{\sin }^2\theta +b^2{\cos }^2\theta \right)}^{3/2}}\frac{d\theta }{dt}\\ \frac{dx}{dt}=\sqrt{a^2{\sin }^2\theta +b^2{\cos }^2\theta }\frac{d\theta }{dt}\end{array}}$

• La coordenada x del centro de masas C

Integramos esta ecuación para obtener la abscisa x en función del tiempo t.

${\displaystyle \begin{array}{l}x={\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\sqrt{a^2{\sin }^2\theta +b^2{\cos }^2\theta }}·d\theta \\ x=a{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\sqrt{1-\frac{a^2-b^2}{a^2}{\cos }^2\theta ·}}d\theta \end{array}}$

Haciendo el cambio de variable θ'=θ+π/2, obtenemos integrales elípticas incompletas de segunda especie

${\displaystyle \begin{array}{l}x=a{\displaystyle \underset{{\theta }_0+\pi /2}{\overset{\theta +\pi /2}{\int }}\sqrt{1-\frac{a^2-b^2}{a^2}{\sin }^2\theta \text{'}·}}d\theta \text{'}=a{\displaystyle \underset{0}{\overset{\theta +\pi /2}{\int }}\sqrt{1-\frac{a^2-b^2}{a^2}{\sin }^2\theta \text{'}·}}d\theta \text{'}-a{\displaystyle \underset{0}{\overset{{\theta }_0+\pi /2}{\int }}\sqrt{1-\frac{a^2-b^2}{a^2}{\sin }^2\theta \text{'}·}}d\theta \text{'}\\ x=a\left\{E\left(\theta +\pi /\mathrm{2,}\frac{a^2-b^2}{a^2}\right)-E\left({\theta }_0+\pi /\mathrm{2,}\frac{a^2-b^2}{a^2}\right)\right\}\end{array}}$

Ecuación del movimiento

La energía cinética es la suma del la energía cinética correspondiente al movimiento de traslación del centro de masas y la energía cinética de rotación alrededor del eje del cilindro.

${\displaystyle \begin{array}{l}{E}_k=\frac{1}{2}m\left({\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2\right)+\frac{1}{2}\left(\frac{1}{4}m\left(a^2+b^2\right)\right){\left(\frac{d\theta }{dt}\right)}^2\\ E_k=\frac{1}{2}m\left(\frac{a^4{\sin }^2\theta +b^4{\cos }^2\theta }{a^2{\sin }^2\theta +b^2{\cos }^2\theta }+\frac{1}{4}\left(a^2+b^2\right)\right){\left(\frac{d\theta }{dt}\right)}^2\end{array}}$

La energía potencial es mgy, tomando el plano horizontal como nivel cero

${\displaystyle E_p=mgy=mg\sqrt{a^2{\sin }^2\theta +b^2{\cos }^2\theta }}$

Calculamos la lagrangiana y la ecuación del movimiento

${\displaystyle \begin{array}{l}L=E_k-E_p=\frac{1}{2}m\left(\frac{a^4{\sin }^2\theta +b^4{\cos }^2\theta }{a^2{\sin }^2\theta +b^2{\cos }^2\theta }+\frac{1}{4}\left(a^2+b^2\right)\right){\left(\frac{d\theta }{dt}\right)}^2-mg\sqrt{a^2{\sin }^2\theta +b^2{\cos }^2\theta }\\ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ m\left(\frac{a^4{\sin }^2\theta +b^4{\cos }^2\theta }{a^2{\sin }^2\theta +b^2{\cos }^2\theta }+\frac{1}{4}\left(a^2+b^2\right)\right)\frac{d^2\theta }{d{t}^2}+2m\frac{\sin \theta \cos \theta ·a^2{b}^2\left(a^2-b^2\right)}{{\left(a^2{\sin }^2\theta +b^2{\cos }^2\theta \right)}^2}{\left(\frac{d\theta }{dt}\right)}^2\\ -m\frac{\sin \theta \cos \theta ·a^2{b}^2\left(a^2-b^2\right)}{{\left(a^2{\sin }^2\theta +b^2{\cos }^2\theta \right)}^2}{\left(\frac{d\theta }{dt}\right)}^2+mg\frac{\sin \theta \cos \theta \left(a^2-b^2\right)}{\sqrt{a^2{\sin }^2\theta +b^2{\cos }^2\theta }}=0\end{array}}$

Simplificando, llegamos a la ecuación diferencial

${\displaystyle \left(\frac{a^4{\sin }^2\theta +b^4{\cos }^2\theta }{a^2{\sin }^2\theta +b^2{\cos }^2\theta }+\frac{1}{4}\left(a^2+b^2\right)\right)\frac{d^2\theta }{d{t}^2}+\frac{\sin \theta \cos \theta ·a^2{b}^2\left(a^2-b^2\right)}{{\left(a^2{\sin }^2\theta +b^2{\cos }^2\theta \right)}^2}{\left(\frac{d\theta }{dt}\right)}^2+g\frac{\sin \theta \cos \theta \left(a^2-b^2\right)}{\sqrt{a^2{\sin }^2\theta +b^2{\cos }^2\theta }}=0}$

Energías

La energía del cilindro que rueda sin deslizar es constante e igual a la inicial

${\displaystyle E=E_k+E_p=\frac{1}{2}m\left(\frac{a^4{\sin }^2\theta +b^4{\cos }^2\theta }{a^2{\sin }^2\theta +b^2{\cos }^2\theta }+\frac{1}{4}\left(a^2+b^2\right)\right){\left(\frac{d\theta }{dt}\right)}^2+mg\sqrt{a^2{\sin }^2\theta +b^2{\cos }^2\theta }}$

Fuerzas

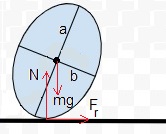
Las fuerzas que actúan sobre el cilindro son:

• el peso mg que actúa en el centro de masas
• la fuerza N que ejerce el plano horizontal sobre el cilindro en el punto de contacto
• la fuerza de rozamiento F_r para que el cilindro ruede sin deslizar, ha de ser menor que la máxima, μ_sN, siendo μ_s el coeficiente estático

Aplicamos la segunda ley de Newton.

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=F_r\\ m\frac{d^{2}y}{d{t}^2}=N-mg\end{array}}$

Despejamos las fuerza por unidad de masa F_r/m y N/m

${\displaystyle \begin{array}{l}\frac{F_r}{m}=\frac{d}{dt}\left(\sqrt{a^2{\sin }^2\theta +b^2{\cos }^2\theta }\frac{d\theta }{dt}\right)=\\ \frac{\left(a^2-b^2\right)\sin \theta \cos \theta }{\sqrt{a^2{\sin }^2\theta +b^2{\cos }^2\theta }}{\left(\frac{d\theta }{dt}\right)}^2+\sqrt{a^2{\sin }^2\theta +b^2{\cos }^2\theta }\frac{d^2\theta }{d{t}^2}\\ \frac{N}{m}=g+\frac{d^{2}y}{d{t}^2}=g+\frac{d^2}{d{t}^2}\left(\sqrt{a^2{\sin }^2\theta +b^2{\cos }^2\theta }\right)=\\ g+\frac{\left(a^2-b^2\right)\sin \theta \cos \theta }{\sqrt{a^2{\sin }^2\theta +b^2{\cos }^2\theta }}\frac{d^2\theta }{d{t}^2}+\left(a^2-b^2\right)\frac{b^2{\cos }^4\theta -a^2{\sin }^4\theta }{{\left(a^2{\sin }^2\theta +b^2{\cos }^2\theta \right)}^{3/2}}{\left(\frac{d\theta }{dt}\right)}^2\end{array}}$

Resultados

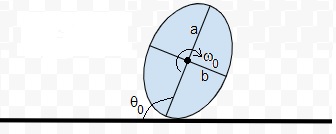
Resolveremos la ecuación diferencial del movimiento con las siguientes condiciones iniciales: en el instante t=0, el ángulo girado es θ₀ y la velocidad angular inicial ω₀ =(dθ/dt)₀

Representamos la energía potencial E_p/(mg) en función del ángulo θ para dos valores del semieje mayor a=1.5, 2, el semieje menor b=1

b=1;
th=110*pi/180; 
hold on
for a=[1.5,2];
    f=@(x) sqrt(a^2*sin(x).^2+b^2*cos(x).^2);
    fplot(f, [pi/2,3*pi/2])
    line([th,2*pi-th],[f(th),f(th)])
end
set(gca,'XTick',pi/2:pi/6:3*pi/2)
set(gca,'XTickLabel',{'\pi/2','2\pi/3','5\pi/6','\pi','7\pi/6','4\pi/3','3\pi/2'})
hold off
grid on
xlabel('\theta')
ylabel('E_p/mg')
title('Energía potencial')

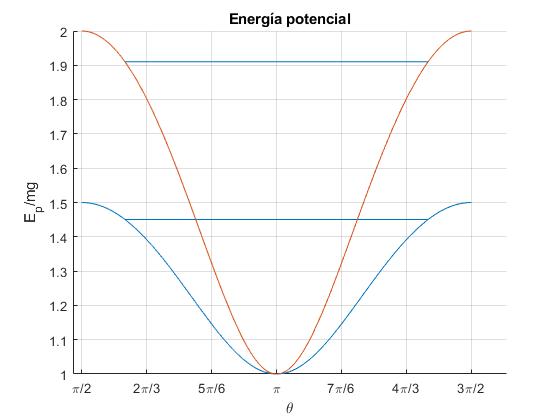
Observamos que la energía potencial es máxima para θ=π/2 y θ=3π/2 (posiciones de equilibrio inestables) y mínima para θ=π (posición de equilibrio estable).

Cuando la velocidad angular inicial es nula, la energía del cilindro es menor que la energía potencial máxima, el cilindro describe oscilaciones de amplitud igual a π-θ₀

Cuando la excentricidad de la elipse es grande, la variación de velocidad angular es grande y el procedimiento numérico ode45 de MATLAB puede que no funcione adecuadamente. Por lo que nos restringiremos a elipses de semiejes, a≈b

Oscilaciones

• Velocidad angular

Representamos la velocidad angular dθ/dt en función del tiempo para un cilindro de base elíptica con a=1.25, y b=1. La posición angular inicial es θ₀=110°, la velocidad angular inicial es nula. La amplitud de la oscilación es 180-110=70°

function elipse
    b=1; %semiejes
    a=1.25;
    th_0=110*pi/180; %posición angular inicial 
    [t,x]=ode45(@eDiferencial,[0,10],[th_0,0]);
    plot(t,x(:,2))
    grid on
    xlabel('t')
    ylabel('d\theta/dt');
    title('Velocidad angular');
    
    %energías
    m1=(a^4*sin(x(:,1)).^2+b^4*cos(x(:,1)).^2)./(a^2*sin(x(:,1)).^2+
b^2*cos(x(:,1)).^2)+(a^2+b^2)/4;
    Energia=m1.*x(:,2).^2/2+9.8*sqrt(a^2*sin(x(:,1)).^2+
b^2*cos(x(:,1)).^2);
    disp(Energia)
    
    function dr=eDiferencial(~, x)
       p1=(a^4*sin(x(1))^2+b^4*cos(x(1))^2)/(a^2*sin(x(1))^2+
b^2*cos(x(1))^2)+(a^2+b^2)/4;
       p2=a^2*b^2*(a^2-b^2)*cos(x(1))*sin(x(1))/(a^2*sin(x(1))^2+
b^2*cos(x(1))^2)^2;
       p3=9.8*(a^2-b^2)*cos(x(1))*sin(x(1))/sqrt(a^2*sin(x(1))^2+
b^2*cos(x(1))^2);
       dr=[x(2);-(p2*x(2)^2+p3)/p1];
    end
end



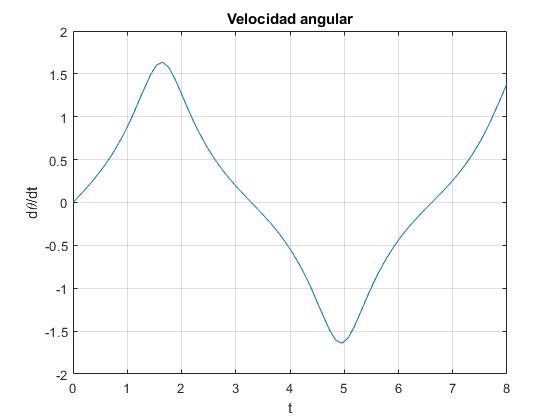
Medimos con el cursor (Data tip) el tiempo t (periodo de la oscilación), que emplea en regresar a la posición inicial con velocidad angular nula, t=6.665 s

Comprobamos que la energía se mantiene aproximadamente constante

   11.9893
   11.9893
....
   12.1375
   12.1375

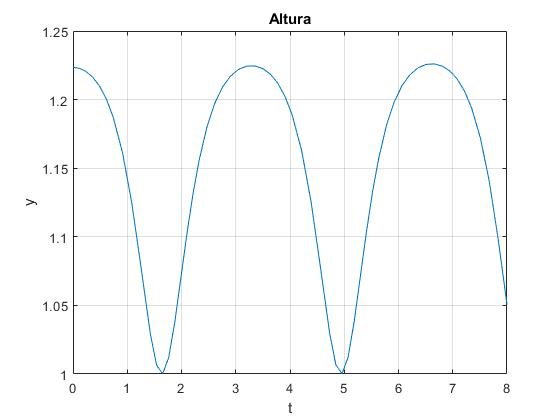
• Altura del centro C de la elipse

Representamos la altura y del centro de la elipse en función del tiempo t. La altura la mínima es b en la posición de equilibrio estable θ=π, la máxima es

${\displaystyle y_{máx}=\sqrt{a^2{\sin }^2{\theta }_0+b^2{\cos }^2{\theta }_0}}$

Para θ₀=110°, y_máx=1.2234 m

...
    yPos=sqrt(a^2*sin(x(:,1)).^2+b^2*cos(x(:,1)).^2);
    plot(t,yPos)
....



• Abscisa x del centro

Tomando como origen el punto de partida del centro del cilindro, representamos la coordenada x del centro C de la elipse en función del tiempo t

...
    e2=1-(b/a)^2;
    xPos=a*(ellipticE(x(:,1)+pi/2,e2)-ellipticE(th_0+pi/2,e2)); 
    plot(t,xPos)
...



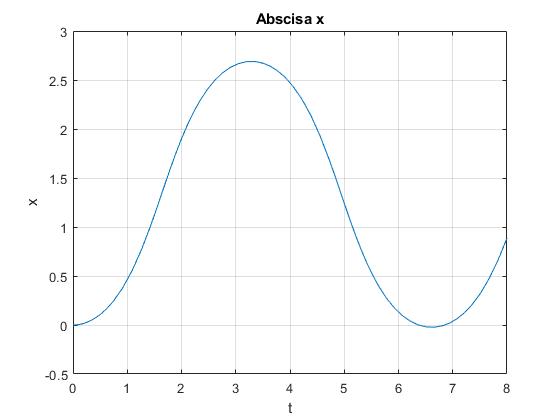
El cilindro regresa al punto de partida, x=0, en el instante t=6.665 s (periodo)

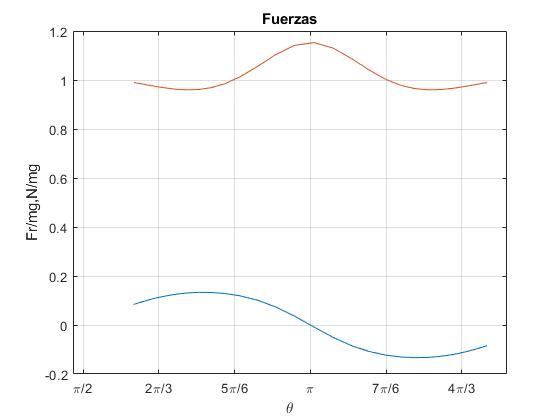
• Fuerzas



Representamos las fuerzas F_r/(mg) y N/(mg) en función del ángulo girado θ durante medio periodo de la oscilación 6.665/2 s. La reacción N presenta un máximo para θ=π (posición de equilibrio estable). La fuerza de rozamiento F_r acelera el cilindro y luego, lo frena, es nula es θ=π

function elipse
    b=1;
    a=1.25;
    th_0=110*pi/180; 
    [t,x]=ode45(@eDiferencial,[0,6.665/2],[th_0,0]);
    [Fr,N]=fuerzas(x(:,1),x(:,2));
    plot(x(:,1),Fr,x(:,1),N)
    set(gca,'XTick',pi/2:pi/6:3*pi/2)
    set(gca,'XTickLabel',{'\pi/2','2\pi/3','5\pi/6','\pi','7\pi/6',
'4\pi/3','3\pi/2'})
    grid on
    xlabel('\theta')
    ylabel('Fr/mg,N/mg');
    title('Fuerzas');
    
   function [Fr,N]=fuerzas(th,w)
       p1=(a^4*sin(th).^2+b^4*cos(th).^2)./(a^2*sin(th).^2+
b^2*cos(th).^2)+(a^2+b^2)/4;
       p2=a^2*b^2*(a^2-b^2)*cos(th).*sin(th)./(a^2*sin(th).^2+
b^2*cos(th).^2).^2;
       p3=9.8*(a^2-b^2)*cos(th).*sin(th)./sqrt(a^2*sin(th).^2+
b^2*cos(th).^2);
       acel=-(p2.*w.^2+p3)./p1;
       temp=(a^2*sin(th).^2+b^2*cos(th).^2);
       Fr=(((a^2-b^2)*sin(th).*cos(th).*w.^2)./sqrt(temp)+
sqrt(temp).*acel)/9.8;
       N=(9.8+((a^2-b^2)*(b^2*cos(th).^4-a^2*sin(th).^4).*w.^2).
/temp.^(3/2)+((a^2-b^2)*cos(th).*sin(th).*acel)./sqrt(temp))/9.8;
    end
    function dr=eDiferencial(~, x)
       p1=(a^4*sin(x(1))^2+b^4*cos(x(1))^2)/(a^2*sin(x(1))^2+
b^2*cos(x(1))^2)+(a^2+b^2)/4;
       p2=a^2*b^2*(a^2-b^2)*cos(x(1))*sin(x(1))/(a^2*sin(x(1))^2+
b^2*cos(x(1))^2)^2;
       p3=9.8*(a^2-b^2)*cos(x(1))*sin(x(1))/sqrt(a^2*sin(x(1))^2+
b^2*cos(x(1))^2);
       dr=[x(2);-(p2*x(2)^2+p3)/p1];
    end
end

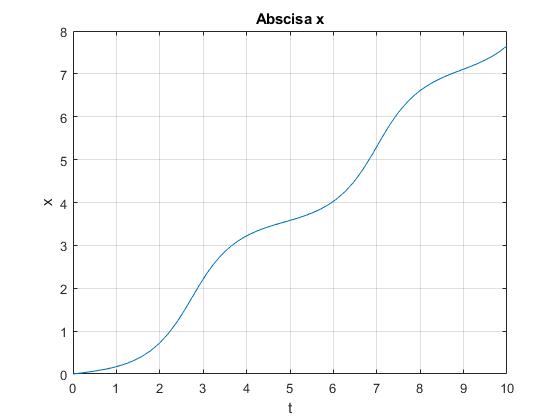
Movimiento de rodar sin deslizar sobre un plano horizontal

Situamos el cilindro en la posición de equilibrio inestable θ₀=π/2 y le porporcionamos una velocidad angular inicial (dθ/dt)₀=0.1 rad/s, de modo que su energía inicial es superior al máximo de energía potencial. El cilindro rodará a lo largo del plano horizontal

function elipse
    b=1;
    a=1.25;
    th_0=pi/2; 
    [t,x]=ode45(@eDiferencial,[0,10],[th_0,0.1]);
    e2=1-(b/a)^2;
    xPos=a*(ellipticE(x(:,1)+pi/2,e2)-ellipticE(th_0+pi/2,e2)); 
    plot(t,xPos)
    grid on
    xlabel('t')
    ylabel('x');
    title('Abscisa x');
    
    function dr=eDiferencial(~, x)
       p1=(a^4*sin(x(1))^2+b^4*cos(x(1))^2)/(a^2*sin(x(1))^2+
b^2*cos(x(1))^2)+(a^2+b^2)/4;
       p2=a^2*b^2*(a^2-b^2)*cos(x(1))*sin(x(1))/(a^2*sin(x(1))^2+
b^2*cos(x(1))^2)^2;
       p3=9.8*(a^2-b^2)*cos(x(1))*sin(x(1))/sqrt(a^2*sin(x(1))^2+
b^2*cos(x(1))^2);
       dr=[x(2);-(p2*x(2)^2+p3)/p1];
    end
end

Actividades

Se introduce

• El semieje mayor a de la elipse, en el control titulado Semieje mayor
• El semieje menor se ha fijado en b=1

• Se puede elegir: Inclinación o Velocidad angular

• En el primer caso, velocidad angular nula, la posición angular inicial θ₀ es 180 grados menos el ángulo de inclinación que se introduce en el control titulado Angulo
• Si la velocidad angular inicial no es nula, se introduce su valor en el control titulado Velocidad, la posición angular inicial es θ₀=90°

Se observa el movimiento del cilindro de base elíptica sobre la plano horizontal. En la parte superior derecha, se proporcionan los datos de

• tiempo t
• Posición (x,y) del centro de la elipse (eje del cilindro)
• La posición angular θ y la velocidad angular dθ/dt de rotación alrededor del eje del cilindro

Utilizando los botones pausa || y paso >| se puede medir el periodo de oscilación, cuando el cilindro retorna a la posición de partida su velocidad angular de rotación es cero.

El programa calcula en cada instante el tanto por ciento de error relativo en la energía o el cociente

${\displaystyle \left|\frac{E-E_0}{E_0}\right|·100}$

donde E es la energía del sistema en cualquier instante t, y E₀ es la energía inicial del sistema.

Este valor se proporciona en caracteres de color rojo en la parte superior. Su valor debe ser siempre cero, o un valor muy pequeño lo que indica que la energía del sistema permanece constante y el programa realiza los cálculos correctamente.

Movimiento de rodar sin deslizar sobre un plano inlinado

El cilindro de base elíptica rueda sin deslizar a lo largo de un plano inclinado un ángulo α. Lo único que cambia es la energía potencial

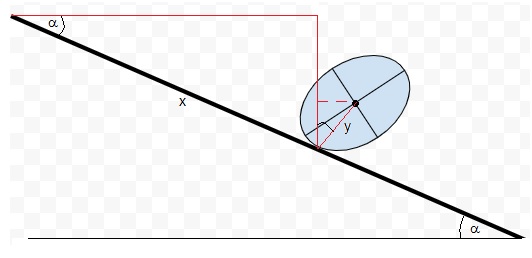
El centro de masa se encuentra por debajo del nivel cero de energía potencial, una altura, xsinα-ycosα.

Calculamos la lagrangiana y la ecuación del movimiento. Solamente tenemos que modificar el término correspondiente a la energía potencial

${\displaystyle \begin{array}{l}L=E_k-E_p=\frac{1}{2}m\left(\frac{a^4{\sin }^2\theta +b^4{\cos }^2\theta }{a^2{\sin }^2\theta +b^2{\cos }^2\theta }+\frac{1}{4}\left(a^2+b^2\right)\right){\left(\frac{d\theta }{dt}\right)}^2+mg\left(x\sin \alpha -y\cos \alpha \right)\\ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ m\left(\frac{a^4{\sin }^2\theta +b^4{\cos }^2\theta }{a^2{\sin }^2\theta +b^2{\cos }^2\theta }+\frac{1}{4}\left(a^2+b^2\right)\right)\frac{d^2\theta }{d{t}^2}+2m\frac{\sin \theta \cos \theta ·a^2{b}^2\left(a^2-b^2\right)}{{\left(a^2{\sin }^2\theta +b^2{\cos }^2\theta \right)}^2}{\left(\frac{d\theta }{dt}\right)}^2\\ -m\frac{\sin \theta \cos \theta ·a^2{b}^2\left(a^2-b^2\right)}{{\left(a^2{\sin }^2\theta +b^2{\cos }^2\theta \right)}^2}{\left(\frac{d\theta }{dt}\right)}^2-mg\left(\frac{\partial x}{\partial \theta }\sin \alpha -\frac{\partial y}{\partial \theta }\cos \alpha \right)=0\end{array}}$

Simplificando, llegamos a la ecuación diferencial

${\displaystyle \begin{array}{l}\left(\frac{a^4{\sin }^2\theta +b^4{\cos }^2\theta }{a^2{\sin }^2\theta +b^2{\cos }^2\theta }+\frac{1}{4}\left(a^2+b^2\right)\right)\frac{d^2\theta }{d{t}^2}+\frac{\sin \theta \cos \theta ·a^2{b}^2\left(a^2-b^2\right)}{{\left(a^2{\sin }^2\theta +b^2{\cos }^2\theta \right)}^2}{\left(\frac{d\theta }{dt}\right)}^2-\\ g\left(\sin \alpha \sqrt{a^2{\sin }^2\theta +b^2{\cos }^2\theta }-\frac{\sin \theta \cos \theta \left(a^2-b^2\right)}{\sqrt{a^2{\sin }^2\theta +b^2{\cos }^2\theta }}\cos \alpha \right)=0\end{array}}$

Cuando la pendiente α=0, obtenemos la ecuación del movimiento del cilindro sobre el plano horizontal

Resolvemos la ecuación diferencial por el procedimiento numérico ode45 con las siguientes condiciones inciales: en el instante t=0, la posición incial es θ₀=π/2, (el eje mayor perpendicular al plano inclinado). Se suelta el cilindro en esta posición y baja rodando sin deslizar a lo largo del plano inclinado

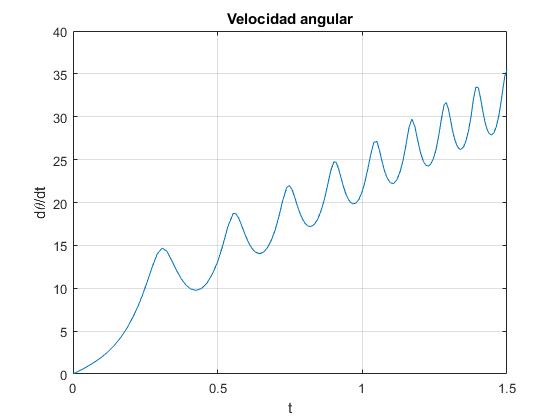
Utilizaremos un cilindro cuya base es una elipse de semiejes a=2.5 y b=2 cm que rueda sobre un plano inclinado α=3.5°. Representamos la velocidad angular dθ/dt de rotación alrededor del eje del cilindro en función del tiempo

function elipse_1
    a=0.025;
    b=0.02;
    aRampa=3.5*pi/180;
    th_0=pi/2;   
    [t,x]=ode45(@eDiferencial,[0,1.5],[th_0,0]);
    yPos=sqrt(a^2*sin(x(:,1)).^2+b^2*cos(x(:,1)).^2);
    e2=1-(b/a)^2;
    xPos=a*(ellipticE(x(:,1)+pi/2,e2)-ellipticE(th_0+pi/2,e2)); 
    plot(t,x(:,2))
    grid on
    xlabel('t')
    ylabel('x');
    title('velocidad angular');
    m1=(a^4*sin(x(:,1)).^2+b^4*cos(x(:,1)).^2)./(a^2*sin(x(:,1)).^2+
b^2*cos(x(:,1)).^2)+(a^2+b^2)/4;
    Energia=m1.*x(:,2).^2/2-9.8*(xPos*sin(aRampa)-yPos*cos(aRampa));
    disp(Energia)
     
    function dr=eDiferencial(~, x)
       p1=(a^4*sin(x(1))^2+b^4*cos(x(1))^2)/(a^2*sin(x(1))^2+
b^2*cos(x(1))^2)+(a^2+b^2)/4;
       p2=a^2*b^2*(a^2-b^2)*cos(x(1))*sin(x(1))/(a^2*sin(x(1))^2+
b^2*cos(x(1))^2)^2;
       p3=9.8*(a^2-b^2)*cos(x(1))*sin(x(1))*cos(aRampa)/sqrt(a^2*sin(x(1))^2+
b^2*cos(x(1))^2)-9.8*sin(aRampa)*sqrt(a^2*sin(x(1))^2+b^2*cos(x(1))^2);
       dr=[x(2);-(p2*x(2)^2+p3)/p1];
    end
end

Comprobamos la conservación de la energía

    0.2445
    0.2445
....
    0.2472
    0.2490

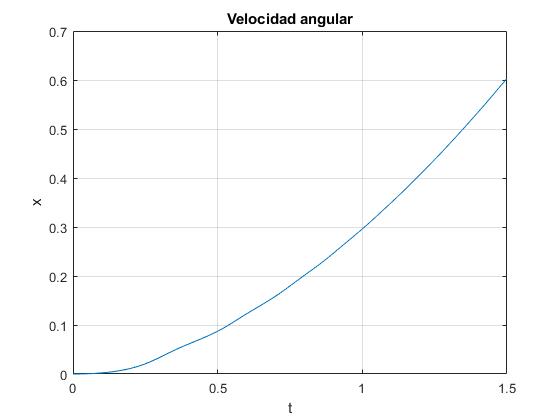
Representamos la posición x del eje del cilindro en función del tiempo

Con una inclinación mayor, el procedimiento ode45 de MATLAB ya no responde adecuadamente, sin embargo, el procedimiento de Runge-Kutta utilizado en la simulación más abajo, sigue funcionando correctamente.

Actividades

Se introduce

• El semieje mayor a de la elipse en cm, en el control titulado Semieje mayor
• El semieje menor se ha fijado en b= 2 cm
• El ángulo del plano inclinado, en el control titulado Pendiente

Observamos el movimiento del cilindro rodando a lo largo del plano inclinado, en la parte superior derecha se proporcionan los datos de

• tiempo t
• Posición (x,y) del centro de la elipse (eje del cilindro)
• La posición angular θ y la velocidad angular dθ/dt de rotación alrededor del eje del cilindro

Referencias

Johan Lindén, Kjell-Mikael Källman, Markus Lindberg. The rolling elliptical cylinder. Am. J. Phys. 89 (4), April 2021, pp. 358-364