Supongamos un asteroide de masa m que se aproxima a un planeta de masa M con velocidad v₀ en el infinito siguiendo una dirección (recta de color rojo) que dista b del centro del planeta tal como se muestra en la figura. A medida que el asteroide se acerca al planeta, va cambiando su velocidad tanto en módulo como en dirección (en color azul), hasta que se aleja hacia el infinito siguiendo una dirección simétrica respecto del eje X, que es la asíntota de la otra rama de la hipérbola.

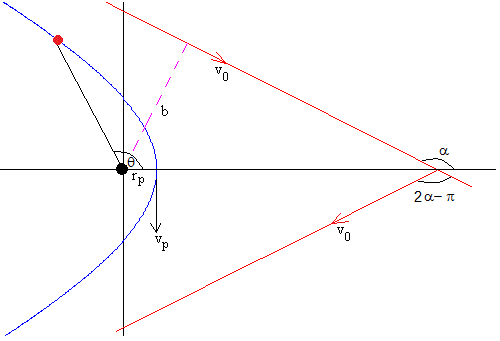
Para analizar el problema supondremos que la masa del asteroide es muy pequeña comparada con la del planeta, m<<M y no tendremos en cuenta la influencia del Sol ni la del resto del los planetas.

La ecuación de la trayectoria es

${\displaystyle r=\frac{d}{1+\epsilon \cos \theta },\epsilon =\sqrt{\text{1}+\frac{2L^{2}E}{m^3{G}^2{M}^2}},d=\frac{L^2}{GM{m}^2}}$

r es la distancia del centro del planeta al asteroide y θ es el ángulo que hace el radio vector que une el asteroide con el centro del planeta con el eje X, tal como se muestra en la figura.

El parámetro ε denominado excentricidad define el tipo de trayectoria. La trayectoria es una hipérbola si ε>1 es decir, si la energía del asteroide E>0.

El ángulo θ no puede superar el ángulo límite, aquél para el cual r→∞, θ_∞=arccos(-1/ε)

Mínima distancia

La energía del asteroide en el infinito es solamente cinética

${\displaystyle E=\frac{1}{2}m{v}_0^2}$

El momento angular es

L=mv₀b

Los parámetros ε y d valen

${\displaystyle \epsilon =\sqrt{\text{1}+\frac{b^2{v}_0^4}{G^2{M}^2}},d=\frac{b^2{v}_0^2}{GM}}$

La distancia más cercana del asteroide al centro del planeta ocurre cuando θ=0

${\displaystyle r_p=\frac{d}{1+\epsilon }=\frac{\frac{b^2{v}_0^2}{GM}}{1+\sqrt{1+\frac{b^2{v}_0^4}{G^2{M}^2}}}}$

Calculamos esta distancia, aplicando la conservación de la energía y del momento angular en el punto P más cercano al centro del planeta.

${\displaystyle \begin{array}{l}L=m{v}_{0}b=m{v}_p{r}_p\\ E=\frac{1}{2}m{v}_0^2=\frac{1}{2}m{v}_p^2-G\frac{Mm}{r_p}\end{array}}$

En este sistema de dos ecuaciones con dos incógnitas despejamos v_p y r_p

${\displaystyle v_p=\frac{GM}{b{v}_0}\left(1+\sqrt{1+\frac{b^2{v}_0^4}{G^2{M}^2}}\right),r_p=\frac{\frac{b^2{v}_0^2}{GM}}{1+\sqrt{1+\frac{b^2{v}_0^4}{G^2{M}^2}}}}$

Dependiendo de las magnitudes M, v₀, b y el radio R del planeta el asteroide choca r_p<R o pasa el planeta. Cuando r_p=R el asteroide choca tangencialmente con el planeta.

Asíntotas

El ángulo para el cual r→∞, es

${\displaystyle \alpha =\arccos \left(-\frac{1}{\epsilon }\right)}$

La dirección de la velocidad del asteroide cambia a medida que se acerca al planeta y luego, cuando se aleja. El cambio en la dirección de la velocidad es φ=2α-π tal como se aprecia en la figura.

tan(φ/2)=-cotα. Utilizando la relación trigonométrica

${\displaystyle \begin{array}{l}1+{\tan }^2\alpha =\frac{1}{{\cos }^2\alpha }\\ \tan \frac{\phi }{2}=\frac{GM}{b{v}_0^2}\end{array}}$

La asíntota de una de las ramas de la hipérbola hace un ángulo α con el eje X y dista b del origen.

Donde x es la intersección de la asíntota con el eje X

${\displaystyle x=\frac{b}{\text{sin}(180-\alpha )}=\frac{b\epsilon }{\sqrt{{\epsilon }^2-1}}}$

e=1.5; %excentricidad
d=1;
r=@(x) d./(1+e*cos(x));
alfa=acos(-1/e); %asíntota
hold on
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[-alfa+0.1,alfa-0.05])
%origen, centro de fuerzas
plot(0,0,'ro', 'markersize',8,'markerfacecolor','y')
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Hipérbola')

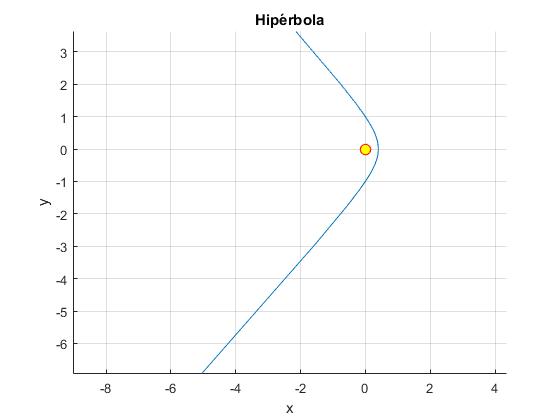
Ejemplo 1

Para el planeta Júpiter cuya masa es M=1.90·10²⁷ kg y radio es R=6.98·10⁶ m.

• Parámetro de impacto, b=2R
• Velocidad en el infinito, v₀=14.6 km/s

G=6.67e-11; %constante G
M=1.90e27; %masa de Júpiter
R=6.98e7; %radio de Júpiter

b=2*R; %parámetro de impacto
v0=14.6*1000; %velocidad
ex=sqrt(1+b^2*v0^4/(G*M)^2); %excentricidad
d=(b*v0)^2/(G*M);

rp=d/(1+ex); %máximo acercamiento
vp=v0*b/rp; %velocidad
fprintf('Máximo acercamiento %1.3f, velocidad (km/s) %3.2f\n'
,rp/R, vp/1000)

Máximo acercamiento 0.232, velocidad (km/s) 126.048

Ejemplo 2

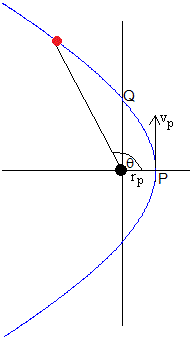
Un proyectil se dispara desde el perigeo, con una velocidad v_p=12 km/s a una altura de h=1000 km sobre la superficie de la Tierra.

Datos

• Masa de la Tierra, m=5.98·10²⁴ kg
• Radio de la Tierra (ecuatorial), R=6 378 km
• Constante G=6.67·10^-11 Nm²/kg²

La energía de proyectil es

${\displaystyle E=\frac{1}{2}m{v}_p^2-G\frac{Mm}{R+h}}$

E=1.7938·10⁷m. Como E>0 el proyectil describe una trayectoria hiperbólica

El momento angular vale, L=mv_pr_p=8.8536·10¹⁰m

La ecuación de la trayectoria en coordenadas polares es

${\displaystyle r=\frac{d}{1+\epsilon \cos \theta },\epsilon =\sqrt{1+\frac{2L^{2}E}{m^3{G}^2{M}^2},}d=\frac{L^2}{GM{m}^2}}$

La excentricidad, ε=1.6636 (ε>1), parámetro d=1.9652·10⁷

El ángulo que hace la asíntota con el eje X

${\displaystyle \alpha =\arccos \left(-\frac{1}{\epsilon }\right)}$

α=126.95°

La velocidad en el infinito es

${\displaystyle E=\frac{1}{2}m{v}_{\infty }^2}$

v_∞=5 990 m/s

El punto Q está en la posición θ=π/2 a una distancia r_q=d=1.9652·10⁷. La velocidad del proyectil en esta posición es

${\displaystyle E=\frac{1}{2}m{v}_q^2-G\frac{Mm}{r_q}}$

v_q=8745 m/s

El proyectil parte del perigeo P y tarda un tiempo t en llegar a Q (θ=π/2)

Calculamos la posición angular F mediante la relación

${\displaystyle \tanh \left(\frac{F}{2}\right)=\sqrt{\frac{\epsilon -1}{\epsilon +1}}\tan \left(\frac{\theta }{2}\right)}$

El resultado es, F=1.0963

Dado F calculamos el tiempo t mediante la relación

${\displaystyle \epsilon \sinh F-F={\left({\epsilon }^2-1\right)}^{3/2}\frac{G^2{M}^2{m}^3}{L^3}t}$

t=2070.5 s, 34 minutos y 30.5 segundos

Hipérbola girada

Vamos a determinar la ecuación de la trayectoria de una partícula que se mueve a una distancia muy grande del centro de fuerzas paralelamente al eje X, con velocidad v₀, tal como se muestra en la figura.

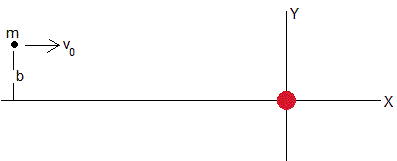
El momento angular L y la energía E valen

${\displaystyle \begin{array}{l}L=mb{v}_0\\ E=\frac{1}{2}m{v}_0^2\end{array}}$

La ecuación de la trayectoria es

${\displaystyle r=\frac{d}{1+\epsilon \cos \left(\theta -{\theta }_0\right)}}$

Calculamos el ángulo θ₀ sabiendo que cuando la partícula está muy alejada del origen θ=π

${\displaystyle \begin{array}{l}\cos \left(\theta -{\theta }_0\right)=\frac{1}{\epsilon }\left(\frac{d}{r}-1\right)\\ r\to \infty \theta \to \pi \\ \cos \left(\pi -{\theta }_0\right)=-\frac{1}{\epsilon }\\ \cos {\theta }_0=\frac{1}{\epsilon }\end{array}}$

La ecuación de la trayectoria es

${\displaystyle r=\frac{d}{1+\epsilon \left(\cos \theta \cos {\theta }_0+\sin \theta \sin {\theta }_0\right)}=\frac{d}{1+\cos \theta +\sqrt{{\epsilon }^2-1}\sin \theta }}$

Teniendo en cuenta que

${\displaystyle \sqrt{{\epsilon }^2-1}=\frac{b{v}_0^2}{GM}\text{,}d=\frac{b^2{v}_0^2}{GM}}$

Expresamos la ecuación de la trayectoria en términos del parámetro adimensional p

${\displaystyle r=\frac{bp}{1+\cos \theta +p\sin \theta }\text{,}p=\frac{b{v}_0^2}{GM}}$

Donde π<θ<π-2α, siendo 2α-π el cambio en la dirección de la velocidad

${\displaystyle \alpha =\arccos \left(-\frac{1}{\epsilon }\right)=\arccos \left(-\frac{1}{\sqrt{p^2+1}}\right)}$

Angulo final

Calculamos de otro modo, el ángulo final θ_f=π-2α. La distancia r→∞, cuando 1+cosθ+psinθ=0. Teniendo en cuenta las relaciones trigonométricas

${\displaystyle \cos \theta =\frac{1}{\sqrt{1+{\tan }^2\theta }},\sin \theta =\frac{\tan \theta }{\sqrt{1+{\tan }^2\theta }}}$

obtenemos

${\displaystyle \sqrt{1+{\tan }^2\theta }+1+p\tan \theta =0}$

Llamando θ=2φ

${\displaystyle \begin{array}{l}\tan \theta =\tan \left(2\phi \right)=\frac{2\tan \phi }{1-{\tan }^2\phi }\\ \frac{1+{\tan }^2\phi }{1-{\tan }^2\phi }+1+p\frac{2\tan \phi }{1-{\tan }^2\phi }=0\\ 1+p\tan \phi =0\end{array}}$

El ángulo final θ_f es

${\displaystyle {\theta }_f=2\arctan \left(-\frac{1}{p}\right)}$

Distancia mínima

La distancia mínima de acercamiento se produce para el ángulo θ_m tal que r=r_m

${\displaystyle \frac{dr}{d\theta }=0\text{,}\tan {\theta }_m=p\text{,}{r}_m=\frac{bp}{1+\sqrt{1+p^2}}}$

La velocidad es máxima v_m cuando la distancia es mínima r_m. La constancia del momento angular se escribe

bv₀=r_mv_m

La ecuación de la trayectoria se puede expresar, alternativamente

${\displaystyle r=\frac{bp}{1+\sqrt{1+p^2}\cos \left(\theta -{\theta }_m\right)}}$

Ejemplo

El planeta Júpiter tiene una masa de 318 veces la de la Tierra (318·5.98·10²⁴=1.9·10²⁷ kg). Su radio es R_J=71 398 km

Una nave espacial se dirige hacia Júpiter a una velocidad v₀=30 km/s con un parámetro de impacto b=250 000 km (≈3.5 radios de Júpiter).

Representamos la trayectoria de la nave espacial

b=250e6; %parámetro de impacto
v0=30e3; %velocidad
M=318*5.98e24; %masa de Júpiter
G=6.67e-11; %constante gravitación
p=b*v0^2/(G*M);
RJ=71492e3; %radio de Júpiter

%trayectoria tomando como unidad el radio de Júpiter
b=250e6/RJ;
r=@(x) b*p./(1+cos(x)+p*sin(x));
th_f=2*atan(-1/p); %ángulo final
th_m=atan(p); %posición mínima distancia
hold on
%proximidades del planeta
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[th_m-pi/2-pi/10,th_m+pi/2+pi/10])
plot(r(th_m-pi/2)*cos(th_m-pi/2),r(th_m-pi/2)*sin(th_m-pi/2),'ro', 
'markersize',4,'markerfacecolor','r')
plot(r(th_m+pi/2)*cos(th_m+pi/2),r(th_m+pi/2)*sin(th_m+pi/2),'ro', 
'markersize',4,'markerfacecolor','r')
%origen, centro de fuerzas
th=(1:360)*pi/180;
fill(cos(th),sin(th),'c')
%asíntotas
alfa=acos(-1/sqrt(1+p^2)); %asíntota
x=b*sqrt(1+p^2)/p;
line([-9,x*cos(pi-alfa)],[b,b],'lineStyle','--', 'color','k')
line([x*cos(pi-alfa),9],[b,tan(2*pi-2*alfa)*(9-x*cos(pi-alfa))+b],
'lineStyle','--', 'color','k')
line([-3,x*cos(pi-alfa)],[-3*tan(pi-alfa),b],'lineStyle','--', 'color','k')
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
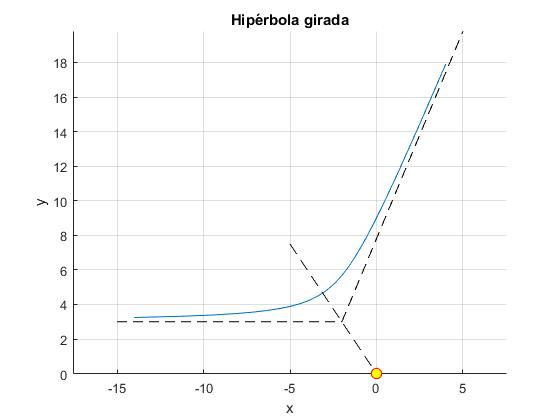
title('Hipérbola girada')

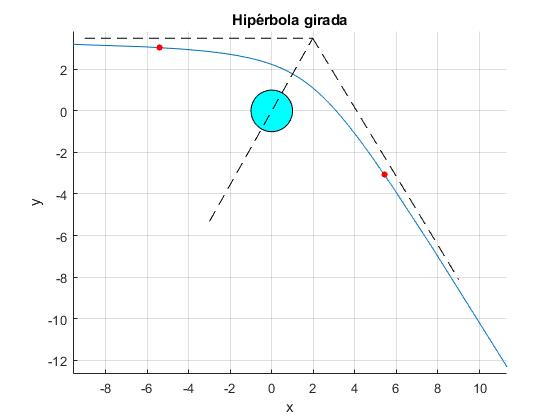
Tiempo de vuelo

Definimos el tiempo de vuelo en las proximidades del planeta como el doble del tiempo que tarda la nave espacial en desplazarse desde la posición θ-θ_m=π/2 hasta la posición θ_m de máximo acercamiento. Los dos puntos de color rojo marcados sobre la trayectoria

En la posición inicial y final, la distancia de la nave espacial al planeta es r=bp mayor que la mínima r_m

Obtenemos el tiempo t, a partir de la constancia del momento angular

${\displaystyle \begin{array}{l}{r}^2\frac{d\theta }{dt}=b{v}_0\\ {\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{b^2{p}^2}{{\left(1+\sqrt{1+p^2}\cos \beta \right)}^2}d\beta }=b{v}_{0}t\\ t_v=2\frac{b{p}^2}{v_0}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\beta }{{\left(1+\sqrt{1+p^2}\cos \beta \right)}^2}}\end{array}}$

Donde la variable β=θ-θ_m, dβ=dθ

Esta integral no es sencilla, buscamos su solucioón en la tabla de integrales (véase las referencias), la encontramos en la página 173, 2.554, n° 3

${\displaystyle {\displaystyle \int \frac{dx}{{\left(a+b\cos x\right)}^n}}=-\frac{1}{(n-1)\left(a^2-b^2\right)}\left\{\frac{b\sin x}{{\left(a+b\cos x\right)}^{n-1}}-{\displaystyle \int \frac{(n-1)a-(n-2)b\cos x}{{\left(a+b\cos x\right)}^{n-1}}dx}\right\}}$

Para n=2, la integral se convierte en

${\displaystyle {\displaystyle \int \frac{dx}{{\left(a+b\cos x\right)}^2}}=-\frac{1}{\left(a^2-b^2\right)}\left\{\frac{b\sin x}{a+b\cos x}-a{\displaystyle \int \frac{dx}{a+b\cos x}}\right\}}$

Encontramos la integral del miembro derecho, en la página 172, 2.553, n° 4 caso b²>a²

${\displaystyle {\displaystyle \int \frac{dx}{a+b\cos x}}=\frac{2}{\sqrt{b^2-a^2}}\ln \left|\frac{(b-a)\tan \left(\frac{x}{2}\right)+\sqrt{b^2-a^2}}{(b-a)\tan \left(\frac{x}{2}\right)-\sqrt{b^2-a^2}}\right|,b^2>a^2}$

En nuestro caso β=x, a=1, $b=\sqrt{1+p^2}$.

${\displaystyle {\displaystyle \int \frac{d\beta }{{\left(1+\sqrt{1+p^2}\cos \beta \right)}^2}}=\frac{1}{p^2}\left\{\frac{\sqrt{1+p^2}\sin \beta }{1+\sqrt{1+p^2}\cos \beta }-\frac{2}{p}\ln \left|\frac{\left(\sqrt{1+p^2}-1\right)\tan \left(\frac{\beta }{2}\right)+p}{\left(\sqrt{1+p^2}-1\right)\tan \left(\frac{\beta }{2}\right)-p}\right|\right\}}$

El tiempo de sobrevuelo de la nave espacial sobre un planeta es

${\displaystyle t_v=2\frac{b}{v_0}\left\{\sqrt{1+p^2}-\frac{2}{p}\ln \left|\frac{\sqrt{1+p^2}-1+p}{\sqrt{1+p^2}-1-p}\right|\right\}}$

Nota: en el artículo de Cameron Reed citado en las referencias la expresión de t_v difiere de la calculada en este apartado

b=250e6; %parámetro de impacto
v0=30e3; %velocidad
M=318*5.98e24; %masa de Júpiter
G=6.67e-11; %constante gravitación
p=b*v0^2/(G*M);
th_f=2*atan(-1/p); 
fprintf('ángulo final %2.1fº\n',th_f*180/pi)
rm=b*p/(1+sqrt(1+p^2)); 
fprintf('mínima distancia al planeta %2.1f km\n',rm/1000)
tv=2*b*(sqrt(1+p^2)-2*log((sqrt(1+p^2)-1+p)/(sqrt(1+p^2)-1-p))/p)/v0; 
fprintf('tiempo sobrevuelo %2.1f h\n',tv/3600)

ángulo final -58.8º
mínima distancia al planeta 146055.2 km
tiempo sobrevuelo 2.4 h

Actividades

Se elige un planeta en el control titulado Planeta

Se introduce

• La velocidad v₀ de un cuerpo celeste (por ejemplo, un asteroide) en el infinito en km/s, en el control titulado Velocidad

• El parámetro de impacto en unidades del radio del planeta en el control titulado Parámetro de impacto

Se pulsa el botón titulado Nuevo

La trayectoria del cuerpo celeste empieza a dibujarse a una distancia r=10·R, diez veces el radio del planeta. En la parte superior derecha, se nos proporciona los datos del tiempo en horas y la distancia en radios del planeta elegido.

Se sugiere al lector:

• Que elija un planeta en la lista, mantenga fija la velocidad v₀ y cambie el parámetro de impacto, distinguiendo las trayectorias que hacen que el asteroide choque con el planeta de aquellas en las que pasa.

Los datos del ejemplo son: Planeta, Júpiter. Parámetro de impacto, b=3.5. Velocidad, v₀=30 km/s,

Datos

Ecuación de la hipérbola en coordenadas rectangulares

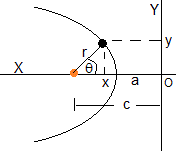
Como en la elipse, establecemos el origen O a una distancia a del vértice de la hipérbola o a una distancia c del foco. La posición (x,y) del cuerpo celeste es

x=c-rcosθ
y=rsinθ

La ecuación de la trayectoria se escribe

${\displaystyle \begin{array}{l}d=r+\epsilon r\cos \theta \\ d=\sqrt{{\left(c-x\right)}^2+y^2}+\epsilon (c-x)\end{array}}$

Elevando al cuadrado

${\displaystyle \begin{array}{l}d-\epsilon (c-x)=\sqrt{{\left(c-x\right)}^2+y^2}\\ d^2+{\epsilon }^2{\left(c-x\right)}^2-2d\epsilon (c-x)={\left(c-x\right)}^2+y^2\\ d^2+{\epsilon }^2{x}^2+{\epsilon }^2{c}^2-2{\epsilon }^{2}cx+2d\epsilon x-2d\epsilon c=x^2+c^2-2cx+y^2\end{array}}$

Teniendo en cuenta la relación entre el parámetro d y a, y la definición de excentricidad ε

${\displaystyle \begin{array}{l}c=a+\frac{d}{1+\epsilon }\\ c=a\epsilon \end{array}\}d=a\left({\epsilon }^2-1\right)}$

La expresión anterior se simplifica notablemente

${\displaystyle \begin{array}{l}{x}^2({\epsilon }^2-1)-y^2=a^2({\epsilon }^2-1)\\ \frac{x^2}{a^2}-\frac{y^2}{a^2({\epsilon }^2-1)}=1\end{array}}$

Fuerzas repulsivas

Sobre la partícula actúa una fuerza repulsiva inversamente proporcional al cuadrado de la distancia r al centro de fuerzas. Por ejemplo, un núcleo fijo de carga Q que repele a una partícula alfa de masa m y carga q. Las ecuación de la trayectoria es la hipérbola

${\displaystyle \begin{array}{l}r=\frac{d}{\epsilon \cos (\theta -{\theta }_0)-1}\\ \epsilon =\sqrt{1+\frac{2L^{2}E}{k^{2}m}}d=\frac{L^2}{km}k=\frac{Qq}{4\pi {\epsilon }_0}\end{array}}$

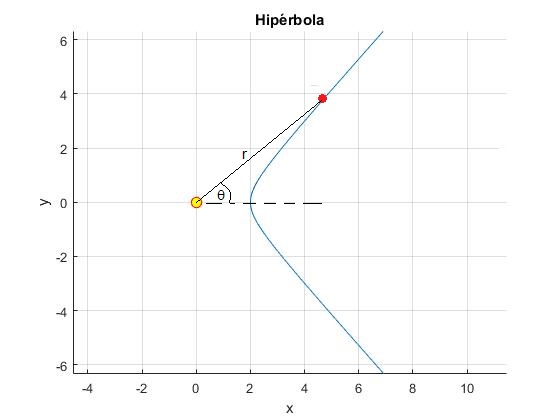
Representamos la hipérbola con parámetro d=1 y excentricidad ε=1.5.

${\displaystyle r=\frac{d}{\epsilon \cos \theta -1}}$

El ángulo θ no puede superar el ángulo límite, aquél para el cual r→∞, θ_∞=arccos(1/ε)

e=1.5; %excentricidad
d=1;
r=@(x) d./(e*cos(x)-1);
alfa=acos(1/e); %asíntota
hold on
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[-alfa+0.1,alfa-0.05])
%origen, centro de fuerzas
plot(0,0,'ro', 'markersize',8,'markerfacecolor','y')
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Hipérbola')

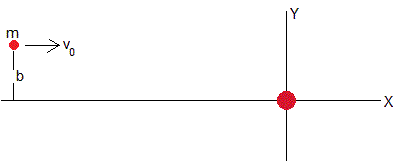
Hipérbola girada

Vamos a determinar la ecuación de la trayectoria de una partícula que se mueve a una distancia muy grande del centro de fuerzas paralelamente al eje X, con velocidad v₀, tal como se muestra en la figura.

El momento angular L y la energía E valen

${\displaystyle \begin{array}{l}L=mb{v}_0\\ E=\frac{1}{2}m{v}_0^2\end{array}}$

La ecuación de la trayectoria es

${\displaystyle r=\frac{d}{\epsilon \cos (\theta -{\theta }_0)-1}}$

Calculamos el ángulo θ₀ sabiendo que cuando la partícula está muy alejada del origen θ=π

${\displaystyle \begin{array}{l}\cos (\theta -{\theta }_0)=\frac{1}{\epsilon }\left(\frac{d}{r}+1\right)\hfill \\ r\to \infty \theta \to \pi \hfill \\ \cos (\pi -{\theta }_0)=\frac{1}{\epsilon }\hfill \\ \cos {\theta }_0=-\frac{1}{\epsilon }\hfill \end{array}}$

La ecuación de la trayectoria es

${\displaystyle r=\frac{d}{\epsilon (\cos \theta \cos {\theta }_0+\sin \theta \sin {\theta }_0)-1}=\frac{d}{\sqrt{{\epsilon }^2-1}\sin \theta -\cos \theta -1}}$

Teniendo en cuenta que

${\displaystyle \sqrt{{\epsilon }^2-1}=\frac{mb{v}_0^2}{k}d=\frac{m{b}^2{v}_0^2}{k}}$

Expresamos la ecuación de la trayectoria en términos del parámetro adimensional p

${\displaystyle r=\frac{bp}{p\sin \theta -\cos \theta -1}p=\frac{mb{v}_0^2}{k}}$

p=1.5; %parámetro adimensional
b=3; %parámetro de impacto
r=@(x) b*p./(p*sin(x)-cos(x)-1);
alfa=acos(1/sqrt(1+p^2)); %asíntota
x=b*sqrt(1+p^2)/p;
%trayectoria
hold on
fplot(@(x) r(x).*cos(x),@(x) r(x).*sin(x),[pi-2*alfa+10*pi/180,pi-10*pi/180])
line([-15,x*cos(pi-alfa)],[b,b],'lineStyle','--', 'color','k')
line([x*cos(pi-alfa),5],[b,tan(2*pi-2*alfa)*(5-x*cos(pi-alfa))+b],
'lineStyle','--', 'color','k')
line([-5,0],[-5*tan(pi-alfa),0],'lineStyle','--', 'color','k')
%origen, centro de fuerzas
plot(0,0,'ro', 'markersize',8,'markerfacecolor','y')
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Hipérbola girada')

Trayectorias de la misma energía

En este apartado, vamos a repetir los cálculos de la página titulada Trayectorias elípticas con el eje girado pero para trayectorias hiperbólicas, energía E>0, en vez de elípticas, E<0

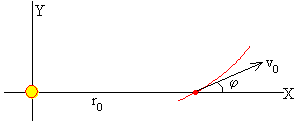
La ecuación de la trayectoria que describe una partícula que dista r₀ del centro de fuerzas, disparada con velocidad inicial v₀, haciendo un ángulo φ entre dicha velocidad y la línea que une el centro fuerzas y el punto de disparo, es.

${\displaystyle r=\frac{d}{1+\epsilon \cos (\theta -{\theta }_0)}}$

La energía E<0 para una trayectoria hiperbólica y el momento angular L, son

${\displaystyle E=\frac{1}{2}m{v}_0^2-G\frac{Mm}{r_0},L=m{r}_0{v}_0\sin \phi }$

Para θ=0, la distancia de la partícula al centro de fuerzas es r=r₀. Obtenemos el valor de θ₀

${\displaystyle \cos \left(-{\theta }_0\right)=\frac{1}{\epsilon }\left(\frac{d}{r_0}-1\right)}$

Conocida la energía E y del momento angular L, determinamos los valores de los parámetros d y ε de la trayectoria. Previamente, definimos el parámetro adimensional

${\displaystyle p=\frac{2GM}{r_0{v}_0^2}}$

Es el cociente entre la energía potencial y la cinética en la posición de partida. Para una trayectoria hiperbólica, la energía total, E>0, p<1

${\displaystyle d=\frac{2r_0{\text{sin}}^2\phi }{p}\epsilon =\sqrt{1-\frac{4{\text{sin}}^2\phi }{p^2}(p-1)}}$

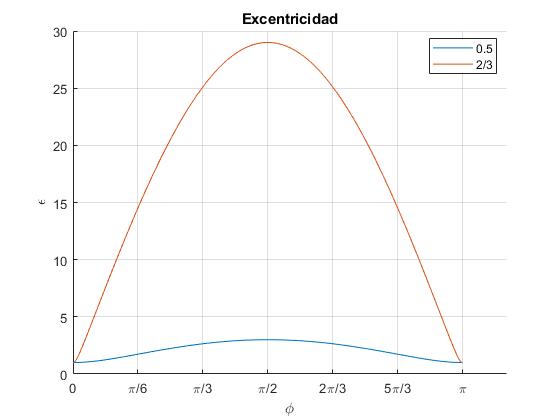
Representamos la excentricidad ε en función del ángulo de disparo φ para dos valores del parámetro p=1/2 y 2/3

e=@(p, x) sqrt(1-(p-1)*(2*sin(x)/p).^2);
hold on
fplot(@(x) e(0.5,x),[0,pi])
fplot(@(x) e(0.2/3,x),[0,pi])
hold off
set(gca,'XTick',0:pi/6:pi)
set(gca,'XTickLabel',{'0','\pi/6','\pi/3','\pi/2','2\pi/3', '5\pi/3','\pi'})
legend('0.5','2/3','location','best')
grid on
xlabel('\phi')
ylabel('\epsilon');
title('Excentricidad')

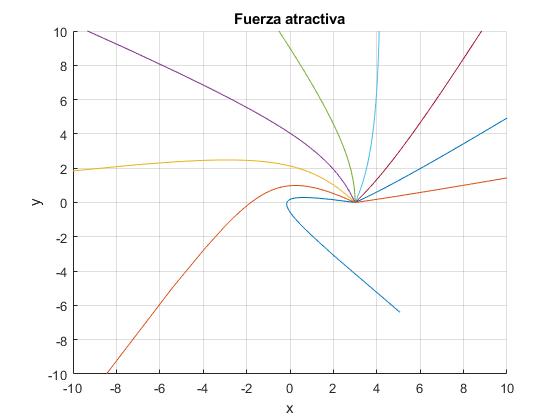
Se representan las trayectorias hiperbólicas de las partículas disparadas desde la posición r₀=3, con ángulos de tiro φ=10°, 30°, 50°, 70°, 90°, 110°, 130°, 150° y 170°, para el valor del parámetro adimensional p=2/3

p=2/3; %energia potencial/energía cinética
r0=3; %posición de partida
hold on
for phi=(170:-20:110)*pi/180
    d=2*r0*sin(phi)^2/p;
    ex=sqrt(1-4*sin(phi)^2*(p-1)/p^2);
    th_0=acos((d/r0-1)/ex);
    r=@(th) d./(1+ex*cos(th-th_0));
    th_lim=th_0+acos(-1/ex);
    fplot(@(th) r(th).*cos(th),@(th) r(th).*sin(th), [0, th_lim-1/180])
end
for phi=(90:-20:10)*pi/180
    d=2*r0*sin(phi)^2/p;
    ex=sqrt(1-4*sin(phi)^2*(p-1)/p^2);
    th_0=-acos((d/r0-1)/ex);
    r=@(th) d./(1+ex*cos(th-th_0));
    th_lim=th_0+acos(-1/ex);
    fplot(@(th) r(th).*cos(th),@(th) r(th).*sin(th), [0, th_lim-1/180])
end

hold off
xlabel('x')
ylabel('y')
grid on
axis([-10,10,-10,10])
title('Fuerza atractiva')

Actividades

Se introduce

• La velocidad v₀ del fragmento en el control titulado Velocidad
• La posición r₀ en el control de edición titulado Posición.

Se pulsa el botón titulado Nuevo

La energía total $E=\frac{1}{2}{v}_0^2-\frac{1}{r_0},E>0$ deberá ser positiva

Se observa las trayectorias de los proyectiles disparados con velocidad v₀ desde la posición r₀ formando ángulos de 30º, 60º, 90º, 120º y 150º con el eje X. La fuerza es atractiva

Fuerzas repulsivas

En el caso de que las fuerzas sean repulsivas, (cargas eléctricas del mismo signo) las trayectorias son hiperbólicas

${\displaystyle r=\frac{d}{\epsilon \cos (\theta -{\theta }_0)-1}}$

Para θ=0, la distancia de la partícula al centro de fuerzas es r=r₀. Obtenemos el valor de θ₀

${\displaystyle \cos \left(-{\theta }_0\right)=\frac{1}{\epsilon }\left(\frac{d}{r_0}+1\right)}$

En función del parámetro p

${\displaystyle d=\frac{2r_0{\text{sin}}^2\phi }{p}\epsilon =\sqrt{1+\frac{4{\text{sin}}^2\phi }{p^2}(p+1)}}$

Recuérdese que la energía potencial es positiva para una fuerza repulsiva

Introducimos los valores de θ₀, excentricidad ε y parámetro d en términos de r₀, p y ángulo φ en la ecuación de la trayectoria. Simplificando, llegamos a la ecuación, similar a la obtenida para trayectorias elípticas

${\displaystyle \frac{r_0}{r}=-\frac{\cos \phi }{\sin \phi }\sin \theta +\cos \theta -\frac{p\left(1-\cos \theta \right)}{2{\sin }^2\phi }}$

La ecuación de la trayectoria depende del ángulo φ con el que se dispara la partícula.
f(r, θ, φ)=0

Deducción alternativa

Al integrar las ecuaciones del movimiento de una partícula bajo la acción de una fuerza repulsiva inversamente proporcional al cuadrado de la distancia r al centro de fuerzas, obtuvimos

${\displaystyle \frac{1}{r}=A\sin \theta +B\cos \theta -\frac{km}{L^2}}$

Derivamos respecto del tiempo y teniendo en cuenta la expresión del momento angular en coordenadas polares, L=mr²(dθ/dt)

${\displaystyle -\frac{m}{L}\frac{dr}{dt}=A\cos \theta -B\sin \theta }$

Los coeficientes A y B se determinan a partir de las condiciones iniciales: θ=0, r=r₀ y las componentes de la velocidad v₀ son:

${\displaystyle \begin{array}{l}{\left(\frac{dr}{dt}\right)}_0=v_0\cos \phi \\ L=m{r}_0{v}_0\sin \phi \end{array}}$

Los coeficientes A y B valen:

${\displaystyle \begin{array}{l}\frac{1}{r_0}=B-\frac{km}{L^2}\hfill \\ -\frac{m}{L}{v}_0\cos \phi =A\hfill \end{array}}$

Obtenemos la misma ecuación de la hipérbola en términos del parámetro adimensional p

${\displaystyle \begin{array}{l}\frac{1}{r}=-\frac{m}{L}{v}_0\cos \phi ·\sin \theta +\left(\frac{1}{r_0}+\frac{km}{L^2}\right)\cos \theta -\frac{km}{L^2}\\ \frac{1}{r}=-\frac{m}{m{r}_0{v}_0\sin \phi }{v}_0\cos \phi ·\sin \theta +\left(\frac{1}{r_0}+\frac{km}{m^2{r}_0^2{v}_0^2{\sin }^2\phi }\right)\cos \theta -\frac{km}{m^2{r}_0^2{v}_0^2{\sin }^2\phi }\\ \frac{1}{r}=-\frac{\cos \phi }{r_0\sin \phi }\sin \theta +\frac{\cos \theta }{r_0}-\frac{k}{m{r}_0^2{v}_0^2{\sin }^2\phi }\left(1-\cos \theta \right)\\ \frac{r_0}{r}=-\frac{\cos \phi }{\sin \phi }\sin \theta +\cos \theta -\frac{p\left(1-\cos \theta \right)}{2{\sin }^2\phi },p=\frac{2k}{m{r}_0{v}_0^2}\end{array}}$

Envolvente

La ecuación de la envolvente de las trayectorias hiperbólicas se obtiene derivando la ecuación, f(r,θ,φ)=0 con respecto a φ e igualando a cero.

${\displaystyle \frac{\partial f}{\partial \phi }=0}$

y combinando ésta con la ecuación de la trayectoria f(r,θ,φ)=0 para eliminar el ángulo φ. La derivada con respecto a φ vale

${\displaystyle \frac{\sin \theta }{{\sin }^2\phi }-\frac{p(1-\cos \theta )}{2}\frac{-2\cos \phi }{{\sin }^3\phi }=0}$

Simplificando llegamos a la expresión

${\displaystyle \tan \phi =-\frac{p(1-\cos \theta )}{\sin \theta }}$

Introducimos esta expresión en la ecuación de la hipérbola, teniendo en cuenta la relación trigonométrica

${\displaystyle {\text{sin}}^2\phi =\frac{{\tan }^2\phi }{1+{\tan }^2\phi }}$

Simplificando y agrupando términos obtenemos

${\displaystyle \begin{array}{l}\frac{r_0}{r}=\frac{{\sin }^2\theta }{p\left(1-\cos \theta \right)}+\cos \theta -\frac{1}{2}\frac{{\sin }^2\theta +p^2{\left(1-\cos \theta \right)}^2}{p\left(1-\cos \theta \right)}\\ \frac{r_0}{r}=\frac{1}{2}\left\{\left(\frac{1}{p}-p\right)+{\left(\sqrt{p}+\frac{1}{\sqrt{p}}\right)}^2\cos \theta \right\}\end{array}}$

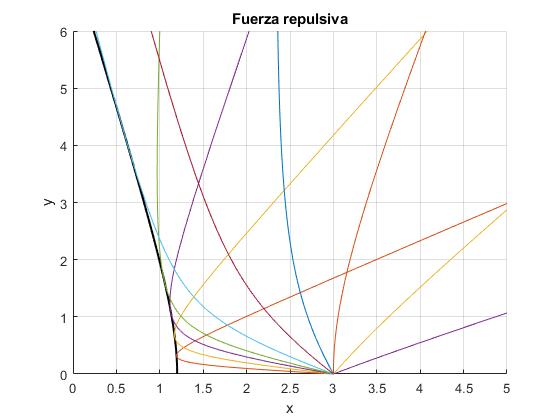
Se representan las trayectorias hiperbólicas de las partículas disparadas desde la posición r₀=3, con ángulos de tiro φ=30°, 60°, 90°, 110°, 130°, 150°, 160°, 165°, 170° y 175°, para el valor del parámetro adimensional p=2/3

Se representa la envolvente, línea de color negro gruesa. No se representan las trayectorias para los ángulos negativos, ya que la figura es simétrica respecto del eje horizontal X

p=2/3; %energia potencial/energía cinética
r0=3; %posición de partida
hold on
for phi=[175, 170,165, 160, 150, 130, 110]*pi/180
    d=2*r0*sin(phi)^2/p;
    ex=sqrt(1+4*sin(phi)^2*(p+1)/p^2);
    th_0=acos((d/r0+1)/ex);
    r=@(th) d./(ex*cos(th-th_0)-1);
    th_lim=th_0+acos(1/ex);
    fplot(@(th) r(th).*cos(th),@(th) r(th).*sin(th), [0, th_lim-1/180])
end
for phi=(90:-30:30)*pi/180
    d=2*r0*sin(phi)^2/p;
    ex=sqrt(1+4*sin(phi)^2*(p+1)/p^2);
    th_0=-acos((d/r0+1)/ex);
    r=@(th) d./(ex*cos(th-th_0)-1);
    th_lim=th_0+acos(1/ex);
    fplot(@(th) r(th).*cos(th),@(th) r(th).*sin(th), [0, th_lim-1/180])
end
th_lim=acos((p-1/p)/(sqrt(p)+1/sqrt(p))^2);
rEnv=@(x) 2*r0./((1/p-p)+(sqrt(p)+1/sqrt(p))^2*cos(x)); %envolvente
fplot(@(th) rEnv(th).*cos(th),@(th) rEnv(th).*sin(th),[0,th_lim], 
'color','k','lineWidth',1.5)

hold off
xlabel('x')
ylabel('y')
grid on
axis([0,5,0,6])
title('Fuerza repulsiva')

Actividades

Se introduce

• La velocidad v₀ del fragmento en el control titulado Velocidad
• La posición r₀ en el control de edición titulado Posición.

Se pulsa el botón titulado Nuevo

Se observa las trayectorias de los proyectiles disparados con velocidad v₀ desde la posición r₀ formando ángulos de 30º, 60º, 90º, 120º y 150º con el eje X. La fuerza es repulsiva

Referencias

I Samengo, R O Barrachina. Rainbow and glory scattering in Coulomb trajectories starting from a point in space. Eur. J. Phys. 15 (1994) pp. 300-308

B Cameron Reed. The single-mass gravitational slingshot. Eur. J. Phys. 35 (2014) 045009

I. S. Gradshteyn, I. M. Ryzhik. Table of Integrals, Series, and Products, Eighth Edition. Elsevier Inc