Componente v_x de la velocidad

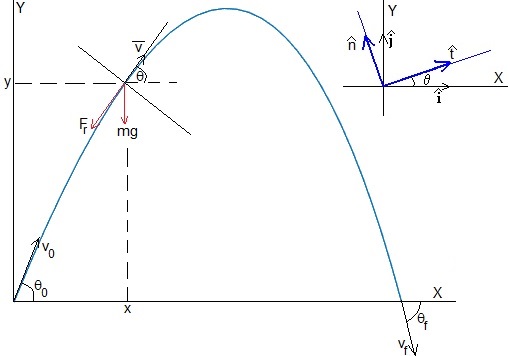
En este apartado, cambiamos de sistema de referencia, y escribimos las ecuaciones del movimiento en la dirección tangencial y en la dirección normal

La relación entre los vectores unitarios (en la parte derecha de la figura) es

${\displaystyle \begin{array}{l}\{\begin{array}{l}\widehat{t}=\cos \theta \widehat{i}+\sin \theta \widehat{j}\\ \widehat{n}=-\sin \theta \widehat{i}+\cos \theta \widehat{j}\end{array}\\ \frac{d\widehat{t}}{dt}=\left(-\sin \theta \widehat{i}+\cos \theta \widehat{j}\right)\frac{d\theta }{dt}=\frac{d\theta }{dt}\widehat{n}\end{array}}$

La derivada del vector velocidad tiene dos componentes

${\displaystyle m\frac{d\overrightarrow{v}}{dt}=m\frac{d\left(v\widehat{t}\right)}{dt}=m\frac{dv}{dt}\widehat{t}+mv\frac{d\widehat{t}}{dt}=m\frac{dv}{dt}\widehat{t}+mv\frac{d\theta }{dt}\widehat{n}}$

Las fuerzas sobre el proyectil son

• El peso, mg
• La fuerza de rozamiento F_r=-mbv² proporcional al cuadrado de la velocidad, cuya dirección es tangencial y sentido contrario al del vector velocidad

La segunda ley de Newton en la dirección tangencial y en la dirección normal, es

${\displaystyle \{\begin{array}{l}m\frac{dv}{dt}=-mg\sin \theta -mb{v}^2\\ mv\frac{d\theta }{dt}=-mg\cos \theta \end{array}}$

La ecuación del movimiento a lo largo del eje X es

${\displaystyle m\frac{d{v}_x}{dt}=-mb{v}^2\cos \theta }$

Cambiamos la variable tiempo t por la variable ángulo θ, empleando la ecuación del movimiento en la dirección normal

${\displaystyle \begin{array}{l}\frac{d{v}_x}{d\theta }\frac{d\theta }{dt}=-b{v}^2\cos \theta \\ \frac{d{v}_x}{d\theta }\left(-\frac{g\cos \theta }{v}\right)=-b{v}^2\cos \theta \\ \frac{d{v}_x}{d\theta }=\frac{b}{g}{v}^3\\ \frac{d{v}_x}{d\theta }=\frac{b}{g}\frac{v_x^3}{{\cos }^3\theta }\end{array}}$

Separamos variables e integramos

${\displaystyle {\displaystyle \underset{v_{0x}}{\overset{v_x}{\int }}\frac{d{v}_x}{v_x^3}}=\frac{b}{g}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\frac{d\theta }{{\cos }^3\theta }}}$

La integral del segundo miembro está resuelta en la página titulada Integrales en el apartado 'Integrales de funciones trigonométricas'. El resultado es

${\displaystyle \begin{array}{l}-\frac{1}{2}\left(\frac{1}{v_x^2}-\frac{1}{v_{0x}^2}\right)=\frac{b}{g}\left(\frac{\sin \theta }{2{\cos }^2\theta }+\frac{1}{2}\ln \left|\tan \theta +\frac{1}{\cos \theta }\right|-\frac{\sin {\theta }_0}{2{\cos }^2{\theta }_0}-\frac{1}{2}\ln \left|\tan {\theta }_0+\frac{1}{\cos {\theta }_0}\right|\right)\\ \frac{1}{v_x^2}=\frac{1}{v_{0x}^2}-\frac{b}{g}\left(\frac{\sin \theta }{{\cos }^2\theta }+\ln \left|\tan \theta +\frac{1}{\cos \theta }\right|-\frac{\sin {\theta }_0}{{\cos }^2{\theta }_0}-\ln \left|\tan {\theta }_0+\frac{1}{\cos {\theta }_0}\right|\right)\end{array}}$

con v_0x=v₀cosθ₀

La camponente v_y de la velocidad y el módulo v valen

${\displaystyle \begin{array}{l}{v}_y=v_x\tan \theta \\ v=\frac{v_x}{\cos \theta }\end{array}}$

A partir, de la segunda ecuación del movimiento expresamos el tiempo t en función del ángulo θ e integramos

${\displaystyle \begin{array}{l}\frac{d\theta }{dt}=-\frac{g\cos \theta }{v}\\ t=-\frac{1}{g}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\frac{v}{\cos \theta }d\theta }\end{array}}$

Expresamos la posición (x, y) de la partícula en función del ángulo θ. La posición inicial de la partícula en el instante t=0 es (x₀, x₀) habitualmente, el origen (0, 0)

${\displaystyle \begin{array}{l}x=x_0+{\displaystyle \underset{0}{\overset{t}{\int }}{v}_{x}dt}=x_0+{\displaystyle \underset{0}{\overset{t}{\int }}{v}_x\frac{d\theta }{\frac{d\theta }{dt}}=}{x}_0+{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}v\cos \theta \frac{d\theta }{\frac{-g\cos \theta }{v}}=}{x}_0-\frac{1}{g}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}{v}^{2}d\theta }\\ y=y_0+{\displaystyle \underset{0}{\overset{t}{\int }}{v}_{y}dt}=y_0+{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}v\sin \theta \frac{d\theta }{\frac{d\theta }{dt}}=}{y}_0-\frac{1}{g}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}{v}^2\tan \theta ·d\theta }\end{array}}$

El alcance y el tiempo de vuelo se obtienen cuando el proyectil llega al suelo, y=0. Se calcula el ángulo final θ_f resolviendo la ecuación transcendente

${\displaystyle y_0-\frac{1}{g}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}{v}^2\tan \theta ·d\theta }=0}$

Una vez conocido el ángulo θ_f, se calcula el alcance R, el tiempo de vuelo, T y la velocidad final de la partícula

${\displaystyle \begin{array}{l}T=-\frac{1}{g}{\displaystyle \underset{{\theta }_0}{\overset{{\theta }_f}{\int }}\frac{v}{\cos \theta }d\theta }\\ R=-\frac{1}{g}{\displaystyle \underset{{\theta }_0}{\overset{{\theta }_f}{\int }}{v}^{2}d\theta }\\ \overrightarrow{v}=v_x({\theta }_f)\left(\widehat{i}+\tan ({\theta }_f)\widehat{j}\right)\end{array}}$

Ejemplo

Se dispara un proyectil con velocidad v₀=60 m/s, haciendo un ángulo θ₀=π/4 (45°). El coeficiente mb=0.0025 kg/m.

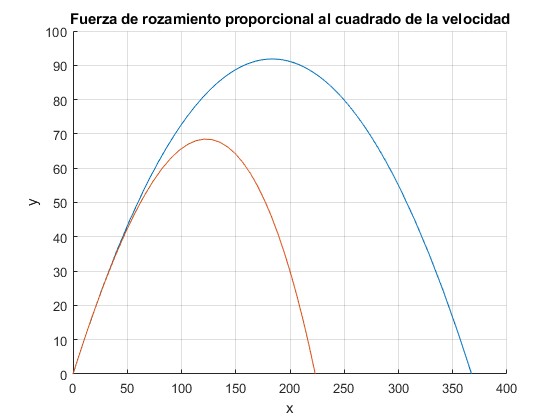
Calculamos el alcance, altura máxima y tiempo de vuelo sin rozamiento (tiro parabólico). Representamos la trayectoria parabólica

Resolvemos el sistema de dos ecuaciones diferenciales por procedimientos numéricos y representamos la trayectoria del proyectil bajo la acción de una fuerza de rozamiento proporcional al cuadrado de la velocidad. Cuando y=0 se interrumpe el proceso de cálculo. Mostramos los valores de las variables

• Tiempo de vuelo, t(end)
• Alcance, x(end,1)
• Componente v_x de la velocidad, x(end,2)
• Componente v_y de la velocidad, x(end,4)

Resolvemos la ecuación transcendente y=0 que nos permite calcular el ángulo final θ_f que hace el vector velocidad con el eje X. Con este valor, calculamos el tiempo de vuelo, el alcance y la altura máxima, utilizando la función integral de MATLAB

function cuadrado
    th_0=pi/4; %ángulo de tiro (45)
    v0=60.0; %velocidad de disparo
    
%tiro parabólico
    H0=v0^2*sin(th_0)^2/(2*9.8); %altura máxima
    R0=v0^2*sin(2*th_0)/9.8; %alcance
    T0=2*v0*sin(th_0)/9.8; %tiempo de vuelo
    hold on
    fplot(@(t) v0*cos(th_0)*t,@(t) v0*sin(th_0)*t-4.9*t.^2, [0,T0])

%rozamiento proporcional al cuadrado de la velocidad
    b=0.0025; %rozamiento
    v0x=v0*cos(th_0); 
    vx=@(x) 1./sqrt(1/v0x^2-b*(sin(x)./cos(x).^2+log(tan(x)+1./cos(x))
-sin(th_0)/cos(th_0)^2-log(tan(th_0)+1/cos(th_0)))/9.8);
    v=@(x) vx(x)./cos(x);
    f=@(x) (v(x).^2).*tan(x);
    g=@(y) integral(f,th_0,y);
    th_f=fzero(g,[-pi*80/180, th_0-eps]);
    hMax=-integral(f,th_0,0)/9.8; %altura máxima
    f=@(x) v(x)./cos(x);
    tVuelo=-integral(f,th_0,th_f)/9.8; %tiempo de vuelo
    f=@(x) v(x).^2;
    xMax=-integral(f,th_0,th_f)/9.8; %alcance
    fprintf('altura máxima %2.1f (%2.1f), alcance %3.1f (%3.1f), 
tiempo de vuelo %1.2f (%1.2f), (vx=%2.2f, vy=%2.2f)\n', hMax, H0, 
xMax, R0, tVuelo, T0, vx(th_f), vx(th_f)*tan(th_f));

%sistema de dos ecuaciones diferenciales
    fg=@(t,x)[x(2);-b*sqrt(x(2)^2+x(4)^2)*x(2); x(4);
-9.8-b*sqrt(x(2)^2+x(4)^2)*x(4)];
    opts=odeset('events',@stop_proyectil);
    [t,x]=ode45(fg,[0,10],[0,v0*cos(th_0),0,v0*sin(th_0)], opts);
    plot(x(:,1),x(:,3)) %trayectoria
    fprintf('tiempo de vuelo %1.2f, alcance %3.1f, (vx=%2.2f, vy=%2.2f) \n', 
t(end), x(end,1), x(end,2),x(end,4));    
    hold off
    grid on
    xlabel('x')
    ylabel('y')
    title('Fuerza de rozamiento proporcional al cuadrado de la velocidad')

   function [detect,stopin,direction]=stop_proyectil(~,x)
        detect=x(3); 
        stopin=1; 
        direction=-1; 
    end
end

altura máxima 68.5 (91.8), alcance 223.3 (367.3), tiempo de vuelo 7.45 (8.66), 
(vx=21.55, vy=-32.74)
tiempo de vuelo 7.45, alcance 223.3, (vx=21.55, vy=-32.74) 

Comparación con el tiro parabólico

Los resultados que se obtienen resolviendo el sistema de dos ecuaciones diferenciales del movimiento, (tiempo de vuelo, alcance, y componenentes v_x y v_y de la velocidad), son similares por los dos procedimientos

Energías

El trabajo de la fuerza de rozamiento modifica la energía del proyectil

${\displaystyle \begin{array}{l}-{\displaystyle \underset{0}{\overset{t}{\int }}mb{v}^{2}ds}=\left(\frac{1}{2}m{v}^2+mgy\right)-\left(\frac{1}{2}m{v}_0^2+mg{y}_0\right)\\ -b{\displaystyle \underset{0}{\overset{t}{\int }}{v}^{3}dt}=\left(\frac{1}{2}{v}^2+gy\right)-\left(\frac{1}{2}{v}_0^2+g{y}_0\right)\\ \frac{b}{g}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\frac{v^4}{\cos \theta }d\theta }=\left(\frac{1}{2}{v}^2+gy\right)-\left(\frac{1}{2}{v}_0^2+g{y}_0\right)\end{array}}$

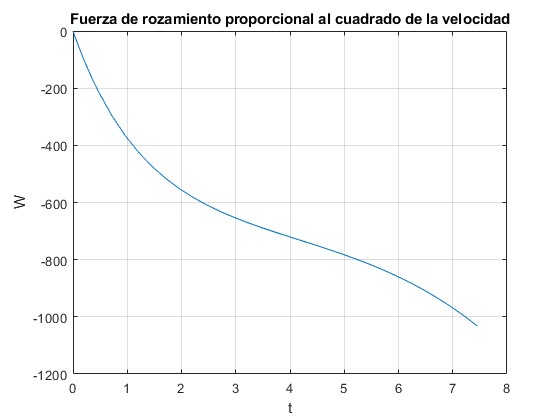
Utilizando el ejemplo anterior, comprobamos el balance energético, el trabajo de la fuerza de rozamiento W=-1031.87 J, es igual a la diferencia entre la energía final $\frac{1}{2}m{v}_f^2=768.1$ y la inicial, $\frac{1}{2}m{v}_0^2=1800.0$

Resolvemos el sistema de dos ecuaciones diferenciales por procedimientos numéricos y representamos el trabajo de la fuerza de rozamiento (diferencia entre la energía en el instante t y la inicial t=0, del proyectil) en función del tiempo

${\displaystyle W=\left(\frac{1}{2}m{v}^2+mgy\right)-\frac{1}{2}m{v}_0^2}$

function cuadrado_3
    th_0=pi/4; %ángulo de tiro (45)
    v0=60.0; %velocidad de disparo
%rozamiento proporcional al cuadrado de la velocidad
    b=0.0025; %rozamiento
    v0x=v0*cos(th_0); 
    vx=@(x) 1./sqrt(1/v0x^2-b*(sin(x)./cos(x).^2+log(tan(x)+
1./cos(x))-sin(th_0)/cos(th_0)^2-log(tan(th_0)+1/cos(th_0)))/9.8);   
    v=@(x) vx(x)./cos(x);
    f=@(x) (v(x).^2).*tan(x);
    g=@(y) integral(f,th_0,y);
    th_f=fzero(g,[-pi*80/180, th_0-eps]);
    
%balance energético
    E0=v0^2/2;
    Ef=v(th_f)^2/2;
    f=@(x) (v(x).^4)./cos(x);
    Wf=b*integral(f,th_0,th_f)/9.8;
    fprintf('Energía inicial %2.1f, final %3.1f, Trabajo %1.2f\n',E0, Ef, Wf);

%solución numérica
    fg=@(t,x)[x(2);-b*sqrt(x(2)^2+x(4)^2)*x(2); x(4);
-9.8-b*sqrt(x(2)^2+x(4)^2)*x(4)];
    opts=odeset('events',@stop_proyectil);
    [t,x]=ode45(fg,[0,10],[0,v0*cos(th_0),0,v0*sin(th_0)], opts);
    W=9.8*x(:,3)+(x(:,2).^2+x(:,4).^2)/2-v0^2/2; 
    plot(t,W)  %Trabajo de la fuerza de rozamiento
    grid on
    xlabel('t')
    ylabel('W')
    title('Fuerza de rozamiento proporcional al cuadrado de la velocidad')

   function [detect,stopin,direction]=stop_proyectil(~,x)
        detect=x(3); 
        stopin=1; 
        direction=-1; 
    end
end

Energía inicial 1800.0, final 768.1, Trabajo -1031.87

Módulo de la velocidad v

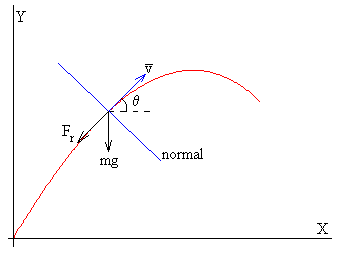
En este apartado, cambiamos de sistema de referencia, y escribimos las ecuaciones del movimiento en la dirección tangencial y en la dirección normal

${\displaystyle \begin{array}{l}m\frac{dv}{dt}=-mb{v}^2-mg\sin \theta \\ m\frac{v^2}{\rho }=mg\cos \theta \end{array}}$

donde ρ es el radio de curvatura de la trayectoria.

En el intervalo de tiempo comprendido entre t y t+dt, la dirección del vector velocidad cambia un ángulo dθ, que es el ángulo entre las tangentes o entre las normales. El móvil se desplaza en este intervalo de tiempo un arco ds=ρ·dθ, tal como se aprecia en la figura.

${\displaystyle \frac{dv}{dt}=\frac{dv}{ds}\frac{ds}{dt}=v\frac{dv}{ds}=\frac{v}{\rho }\frac{dv}{d\theta }}$

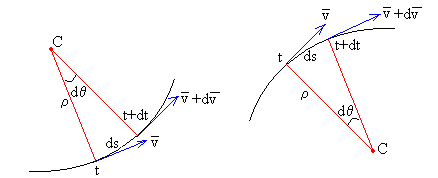
Hemos de tener en cuenta que la curvatura de la trayectoria es negativa (figura de la derecha). La curva queda a la derecha de la tangente tomada en sentido de las x crecientes. La igualdad anterior se escribe para este caso

${\displaystyle \frac{dv}{dt}=-\frac{v}{\rho }\frac{dv}{d\theta }}$

Las ecuaciones del movimiento en la dirección tangencial y en la dirección normal se convierten en una única ecuación diferencial de primer orden.

${\displaystyle \begin{array}{l}\frac{g\cos \theta }{v}\frac{dv}{d\theta }=b{v}^2+g\sin \theta \\ \frac{1}{v^3}\frac{dv}{d\theta }-\frac{1}{v^2}\tan \theta =\frac{b}{g\cos \theta }\end{array}}$

Haciendo el cambo de variable u=1/v²

${\displaystyle \frac{du}{d\theta }+2\tan \theta ·u=\frac{-2b}{g\cos \theta }}$

Esta ecuación es del tipo lineal (véase Puig Adam P., Curso teórico-práctico de Ecuaciones Diferenciales aplicado a la Física y Técnica. Biblioteca Matemática, 1970. págs. 29-30)

Buscamos una solución de la forma u=w(θ)·z(θ)

${\displaystyle \begin{array}{l}w\frac{dz}{d\theta }+z\frac{dw}{d\theta }+2\tan \theta ·(w·z)=\frac{-2b}{g\cos \theta }\\ w\left(\frac{dz}{d\theta }+2\tan \theta ·z\right)+z\frac{dw}{d\theta }=\frac{-2b}{g\cos \theta }\end{array}}$

Hacemos que

${\displaystyle \frac{dz}{d\theta }+2\tan \theta ·z=0}$

La integral se calcula fácilmente

${\displaystyle \begin{array}{l}\frac{dz}{z}=-2\tan \theta {\displaystyle \int \frac{dz}{z}}=-2{\displaystyle \int \tan \theta ·d\theta }\\ \ln z=2\ln \cos \theta +\ln C\\ z=C_1{\cos }^2\theta \end{array}}$

Nos queda ahora que

${\displaystyle \begin{array}{l}z\frac{dw}{d\theta }=\frac{-2b}{g\cos \theta }\frac{dw}{d\theta }=\frac{-2b}{C_{1}g{\cos }^3\theta }\\ w=\frac{-2b}{C_{1}g}{\displaystyle \int \frac{d\theta }{{\cos }^3\theta }}\end{array}}$

Integramos por partes

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{d\theta }{{\cos }^3\theta }=\frac{\tan \theta }{\cos \theta }}-{\displaystyle \int \frac{d\theta }{{\cos }^3\theta }+{\displaystyle \int \frac{d\theta }{\cos \theta }}}\\ {\displaystyle \int \frac{d\theta }{{\cos }^3\theta }=\frac{1}{2}\frac{\tan \theta }{\cos \theta }}+\frac{1}{2}{\displaystyle \int \frac{d\theta }{\cos \theta }}\end{array}}$  

Resolvemos esta última integral haciendo el cambio de variable t=tan(θ/2)

${\displaystyle \begin{array}{l}\cos \theta ={\cos }^2(\theta /2)-{\sin }^2(\theta /2)=\frac{1}{1+t^2}-\frac{t^2}{1+t^2}=\frac{1-t^2}{1+t^2}\\ d\theta =\frac{2}{1+t^2}dt\\ {\displaystyle \int \frac{d\theta }{\cos \theta }}={\displaystyle \int \frac{2dt}{1-t^2}=}{\displaystyle \int \frac{dt}{1-t}}+{\displaystyle \int \frac{dt}{1+t}=}\ln \frac{1+t}{1-t}=\\ \ln \frac{1+\tan (\theta /2)}{1-\tan (\theta /2)}=\ln \frac{\cos (\theta /2)+\sin (\theta /2)}{\cos (\theta /2)-\sin (\theta /2)}=\ln \frac{1+\sin \theta }{\cos \theta }\\ {\displaystyle \int \frac{d\theta }{\cos \theta }}=\ln \left|\tan \theta +\frac{1}{\cos \theta }\right|\end{array}}$

De este modo,

${\displaystyle {\displaystyle \int \frac{d\theta }{{\cos }^3\theta }=}\frac{1}{2}\frac{\tan \theta }{\cos \theta }+\frac{1}{2}\ln \left(\tan \theta +\frac{1}{\cos \theta }\right)=\frac{1}{2}\frac{\sin \theta }{{\cos }^2\theta }+\frac{1}{2}\ln \tan \left(\frac{\theta }{2}+\frac{\pi }{4}\right)}$

Hemos utilizado la relación trigonométrica

${\displaystyle \tan \left(\frac{\theta }{2}+\frac{\pi }{4}\right)=\frac{\sin \left(\frac{\theta }{2}+\frac{\pi }{4}\right)}{\cos \left(\frac{\theta }{2}+\frac{\pi }{4}\right)}=\frac{\cos \frac{\theta }{2}+\sin \frac{\theta }{2}}{\cos \frac{\theta }{2}-\sin \frac{\theta }{2}}=\frac{1+2\cos \frac{\theta }{2}\sin \frac{\theta }{2}}{{\cos }^2\frac{\theta }{2}-{\sin }^2\frac{\theta }{2}}=\frac{\sin \theta +1}{\cos \theta }}$

Finalmente,

${\displaystyle \begin{array}{l}w=\frac{-2b}{C_{1}g}\left\{\frac{1}{2}\frac{\sin \theta }{{\cos }^2\theta }+\frac{1}{2}\ln \tan \left(\frac{\theta }{2}+\frac{\pi }{4}\right)\right\}+C_2\hfill \\ u=w·z={\cos }^2\theta \left\{C_2-\frac{b}{g}\left(\frac{\sin \theta }{{\cos }^2\theta }+\ln \tan \left(\frac{\theta }{2}+\frac{\pi }{4}\right)\right)\right\}\hfill \\ v^2=\frac{1}{{\cos }^2\theta }{\left\{C_2-\frac{b}{g}\left(\frac{\sin \theta }{{\cos }^2\theta }+\ln \tan \left(\frac{\theta }{2}+\frac{\pi }{4}\right)\right)\right\}}^{-1}\hfill \end{array}}$

Se calcula la constante de integración C₂ a partir de las condiciones iniciales: en el instante t=0, la velocidad de disparo es v₀ y hace un ángulo θ₀ con la horizontal (véase la figura más abajo)

${\displaystyle v_0^2=\frac{1}{{\cos }^2{\theta }_0}{\left\{C_2-\frac{b}{g}\left(\frac{\sin {\theta }_0}{{\cos }^2{\theta }_0}+\ln \tan \left(\frac{{\theta }_0}{2}+\frac{\pi }{4}\right)\right)\right\}}^{-1}}$

La función que relaciona el módulo de la velocidad v y el ángulo θ, que forma la dirección de la velocidad (tangente a la trayectoria) con la horizontal es

${\displaystyle \begin{array}{l}\begin{array}{l}{v}^2=\frac{1}{{\cos }^2\theta }{\left\{\frac{1}{v_0^2{\cos }^2{\theta }_0}+\frac{b}{g}\left(f({\theta }_0)-f(\theta )\right)\right\}}^{-1}\\ v=\frac{v_0\cos {\theta }_0}{\cos \theta \sqrt{1+\frac{b}{g}{v}_0^2{\cos }^2{\theta }_0\left(f({\theta }_0)-f(\theta )\right)}}\end{array}\hfill \\ f(\theta )=\frac{\sin \theta }{{\cos }^2\theta }+\ln \tan \left(\frac{\theta }{2}+\frac{\pi }{4}\right)\hfill \end{array}}$

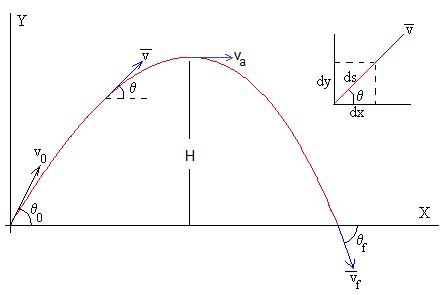
La altura máxima (del vértice de la trayectoria) se obtiene para θ=0, la velocidad cuya dirección es horizontal vale, entonces

${\displaystyle v_a=\frac{v_0\cos {\theta }_0}{\sqrt{1+\frac{b}{g}{v}_0^2\left(\sin {\theta }_0+{\cos }^2{\theta }_0·\ln \tan \left(\frac{{\theta }_0}{2}+\frac{\pi }{4}\right)\right)}}}$

Posición del proyectil

dx=ds·cosθ=ρdθ·cosθ

Utilizando la ecuación del movimiento en la dirección normal, y teniendo en cuenta que la trayectoria tiene curvatura negativa

${\displaystyle \begin{array}{l}dx=-\frac{v^2}{g\cos \theta }\cos \theta ·d\theta =-\frac{v^2}{g}d\theta \hfill \\ x=x_0-\frac{1}{g}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}{v}^{2}d\theta }\hfill \end{array}}$

Del mismo modo

dy=ds·sinθ=ρdθ·sinθ

${\displaystyle \begin{array}{l}dy=-\frac{v^2}{g\cos \theta }\sin \theta ·d\theta =-\frac{v^2}{g}\tan \theta ·d\theta \hfill \\ y=y_0-\frac{1}{g}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}{v}^2\tan \theta ·d\theta }\hfill \end{array}}$

Donde (x₀, y₀) es la posición inicial, normalmente el origen

La altura máxima se obtiene para θ=0

${\displaystyle H=-\frac{1}{g}{\displaystyle \underset{{\theta }_0}{\overset{0}{\int }}{v}^2\tan \theta ·d\theta }}$

Tiempo de vuelo

ds=v·dt
ρdθ= v·dt

${\displaystyle \begin{array}{l}dt=-\frac{v^2}{vg\cos \theta }d\theta =-\frac{v}{g\cos \theta }d\theta \\ t=-\frac{1}{g}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\frac{v}{\cos \theta }d\theta }\end{array}}$

Alcance

Calculamos el ángulo θ_f final que forma la dirección de la velocidad cuando y=0, resolviendo la ecuación trascendente mediante fzero de MATLAB.

${\displaystyle {\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}{v}^2\tan \theta ·d\theta }}$

Conocido el ángulo final θ_f se calcula el alcance R=x-x₀ y el tiempo de vuelo T, calculando las integrales por el procedimiento numérico integral de MATLAB

${\displaystyle R=-\frac{1}{g}{\displaystyle \underset{{\theta }_0}{\overset{{\theta }_f}{\int }}{v}^{2}d\theta },T=-\frac{1}{g}{\displaystyle \underset{{\theta }_0}{\overset{{\theta }_f}{\int }}\frac{v}{\cos \theta }d\theta }}$

Ejemplo

Se dispara un proyectil con velocidad v₀=60 m/s, haciendo un ángulo θ₀=π/4 (45°). El coeficiente mb=0.0025 kg/m. Calculamos

• el alcance, R
• el tiempo de vuelo, T
• la altura máxima, H
• el ángulo final, θ_f
• la velocidad final, v_f

th_0=45*pi/180; %ángulo de tiro
v0=60.0; %velocidad de disparo

%rozamiento proporcional al cuadrado de la velocidad
b=0.0025;
h=@(x) tan(x)./cos(x)+log(abs(tan(x)+1./cos(x)));
%inversa de v^2
inv_v2=@(x) (cos(x).^2).*(1.0/(v0*cos(th_0))^2-b*(h(x)-h(th_0))/9.8); 
f=@(x) -tan(x)./(9.8*inv_v2(x));
g=@(y) integral(f,th_0,y);
th_f=fzero(g,[-pi*80/180, th_0-eps]);
hMax=integral(f,th_0,0);
f=@(x) -1./(9.8*inv_v2(x));
xMax=integral(f,th_0,th_f);
f=@(x) -1./(9.8*cos(x).*sqrt(inv_v2(x)));
tVuelo=integral(f,th_0,th_f);
fprintf('Exacta: altura máxima %2.1f, alcance %3.1f, tiempo de vuelo %1.2f, 
ángulo final %2.1f, velocidad final %2.2f\n', hMax, xMax, tVuelo,
 th_f*180/pi, 1/sqrt(inv_v2(th_f)))

Exacta: altura máxima 68.5, alcance 223.3, tiempo de vuelo 7.45, 
ángulo final -56.6, velocidad final 39.20

Obtenemos los mismos resultados que en el primer apartado

Fórmulas analíticas aproximadas

Existen fórmulas que nos proporcionan, el alcance, la altura máxima el tiempo de vuelo, etc, con gran precisión, véase el ártículo de Chudinov

Cuando b=0 (sin rozamiento), las fórmulas de la tercera columna se convierten en las fórmulas de la segunda columna

Ejemplo

Se dispara un proyectil con velocidad v₀=60 m/s, haciendo un ángulo θ₀=π/4 (45°). El coeficiente mb=0.0025 kg/m. Calculamos

• el alcance, R
• el tiempo de vuelo, T
• la altura máxima, H
• el ángulo final, θ_f
• la velocidad final, v_f

con las fórmulas analíticas aproximadas de la tercera columna de la tabla y las comparamos con los obtenidos resolviendo el sistema de dos ecuaciones diferenciales por el procedimiento ode45 de MATLAB. Representamos la trayectoria y obtenida numéricamente y la analítica aproximada

function cuadrado_4
    b=0.0025; %parámetro
    th_0=pi/4;  %ángulo de tiro (45)
    v0=60; %velocidad de disparo
    %solución analítica aproximada
    hMax=v0^2*sin(th_0)^2/(2*9.8+b*v0^2*sin(th_0)); %altura máxima
    tVuelo=2*sqrt(2*hMax/9.8); %tiempo de vuelo
    va=v0*cos(th_0)/sqrt(1+b*v0^2*(sin(th_0)+cos(th_0)^2*
log(tan(th_0/2+pi/4)))/9.8);
    xMax=va*tVuelo; %alcance
    xa=sqrt(xMax*hMax/tan(th_0));
    th_f=-atan(xMax*hMax/(xMax-xa)^2);
%inversa de v^2
    h=@(x) tan(x)./cos(x)+log(abs(tan(x)+1./cos(x)));
    inv_v2=@(x) (cos(x).^2).*(1.0/(v0*cos(th_0))^2-b*(h(x)-h(th_0))/9.8); 
    fprintf('Analítica aprox.: altura máxima %2.1f, alcance %3.1f, 
    tiempo de vuelo %1.2f, ángulo final %2.1f, velocidad final %2.2f\n', hMax, 
xMax, tVuelo, th_f*180/pi, 1/sqrt(inv_v2(th_f)))
    %solución numérica
    % x(1) es x, x(2) es dx/dt, x(3) es y, x(4) es dy/dt
    fg=@(t,x)[x(2);-b*sqrt(x(2)^2+x(4)^2)*x(2); x(4);
-9.8-b*sqrt(x(2)^2+x(4)^2)*x(4)];
    opts=odeset('events',@stop_proyectil);
    hold on
    [t,x]=ode45(fg,[0,10],[0,v0*cos(th_0),0,v0*sin(th_0)], opts);      
    plot(x(:,1),x(:,3)) %trayectoria
    fprintf('Numérica: alcance %3.1f, tiempo de vuelo %1.2f, ángulo final %2.1f, 
velocidad final %2.2f\n', x(end,1), t(end), atan(x(end,4)/x(end,2))*180/pi, 
sqrt(x(end,4)^2+x(end,2)^2))
  f=@(x) hMax*x.*(xMax-x)./(xa^2+(xMax-2*xa)*x);
    fplot(f,[0,xMax])
    hold off
    grid on
    legend('numérica','analítica','location','best')
    xlabel('x')
    ylabel('y')
    title('Fuerza de rozamiento proporcional al cuadrado de la velocidad')

    function [detect,stopin,direction]=stop_proyectil(~,x)
        detect=x(3); 
        stopin=1; 
        direction=-1; 
    end
end

Analítica aprox.: altura máxima 69.3, alcance 222.7, tiempo de vuelo 7.52, 
ángulo final -57.9, velocidad final 39.89
Numérica: alcance 223.3, tiempo de vuelo 7.45, ángulo final -56.6, 
velocidad final 39.20

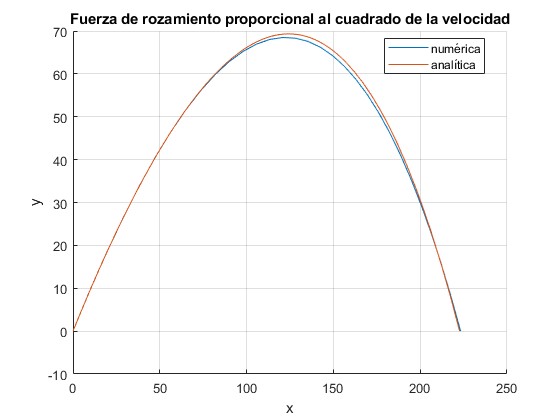
Recogemos en la tabla, la solución 'exacta', la numérica y la analítica aproximada

• 'Exacta' se refiere al cálculo de las magitudes (tiempo de vuelo, alcance, altura máxima) integrando numéricamente, mediante integral de MATLAB. El ángulo final, se obtiene mediante fzero de MATLAB

• Numérica, se refiere a la solución numérica del sistema de dos ecuaciones diferenciales, mediante ode45 de MATLAB

• Analítica aprox., se refiere al cálculo de dichas magnitudes de acuerdo con fórmulas de la tercera columna de la tabla

Alcance máximo

Las expresiones analíticas aproximadas nos permiten calcular el ángulo de tiro θ₀ (en adelante θ) para el cual el alcance R es máximo

${\displaystyle \begin{array}{l}R=v_{a}T=2v_a\sqrt{\frac{2H}{g}}=2\frac{v_0\cos \theta }{\sqrt{1+\frac{b}{g}{v}_0^2\left(\sin \theta +{\cos }^2\theta ·\ln \tan \left(\frac{\theta }{2}+\frac{\pi }{4}\right)\right)}}\sqrt{\frac{2}{g}\frac{v_0^2{\sin }^2\theta }{2g+b{v}_0^2\sin \theta }}\\ =\frac{2\sqrt{2}{v}_0^2\sin \theta \cos \theta }{\sqrt{2g^2+3gb{v}_0^2\sin \theta +b^2{v}_0^4{\sin }^2\theta +2gb{v}_0^2{\cos }^2\theta ·\ln \tan \left(\frac{\theta }{2}+\frac{\pi }{4}\right)+b^2{v}_0^4{\cos }^2\theta \sin \theta ·\ln \tan \left(\frac{\theta }{2}+\frac{\pi }{4}\right)}}\end{array}}$

Para calcular el máximo de la expresión, no es necesario completar la derivada respecto de θ de un cociente, tal como se indica

${\displaystyle \begin{array}{l}R=\frac{a}{\sqrt{b}}\\ \frac{dR}{d\theta }=\frac{\frac{da}{d\theta }\sqrt{b}-\frac{db}{d\theta }\frac{a}{2\sqrt{b}}}{b}=0\\ 2b\frac{da}{d\theta }-a\frac{db}{d\theta }=0\end{array}}$

En la larga expresión es necesario calcular en dos ocasiones la derivada de

${\displaystyle \frac{d}{d\theta }\ln \tan \left(\frac{\theta }{2}+\frac{\pi }{4}\right)=\frac{1}{2}\frac{\frac{1}{{\cos }^2\left(\frac{\theta }{2}+\frac{\pi }{4}\right)}}{\tan \left(\frac{\theta }{2}+\frac{\pi }{4}\right)}=\frac{1}{\sin \left(\theta +\frac{\pi }{2}\right)}=\frac{1}{\cos \theta }}$

La derivada de R respecto de θ, es una larga expresión

${\displaystyle \begin{array}{l}\frac{dR}{d\theta }=2\left({\cos }^2\theta -{\sin }^2\theta \right)\left(2g^2+3gb{v}_0^2\sin \theta +b^2{v}_0^4{\sin }^2\theta +2gb{v}_0^2{\cos }^2\theta ·\ln \tan \left(\frac{{\theta }_0}{2}+\frac{\pi }{4}\right)+b^2{v}_0^4{\cos }^2\theta \sin \theta ·\ln \tan \left(\frac{{\theta }_0}{2}+\frac{\pi }{4}\right)\right)\\ -\sin \theta \cos \theta \left(5gb{v}_0^2\cos \theta +3b^2{v}_0^4\sin \theta \cos \theta -4gb{v}_0^2\cos \theta \sin \theta ·\ln \tan \left(\frac{{\theta }_0}{2}+\frac{\pi }{4}\right)-2b^2{v}_0^4\cos \theta {\sin }^2\theta ·\ln \tan \left(\frac{{\theta }_0}{2}+\frac{\pi }{4}\right)+b^2{v}_0^4{\cos }^3\theta ·\ln \tan \left(\frac{{\theta }_0}{2}+\frac{\pi }{4}\right)\right)=0\end{array}}$

Simplificando, obtenemos la ecuación trascendente

${\displaystyle 4g^2\left({\cos }^2\theta -{\sin }^2\theta \right)+gb{v}_0^2\left({\cos }^2\theta \sin \theta -6{\sin }^3\theta +4{\cos }^4\theta ·\ln \tan \left(\frac{{\theta }_0}{2}+\frac{\pi }{4}\right)\right)+b^2{v}_0^4\left({\cos }^4\theta \sin \theta ·\ln \tan \left(\frac{{\theta }_0}{2}+\frac{\pi }{4}\right)-{\cos }^2\theta {\sin }^2\theta -2{\sin }^4\theta \right)=0}$

En el siguiente script, establecemos la velocidad inicial v₀=40 m/s, y el coeficiente mb=0.000625·9.8 kg/m.

• Representamos el alcance en función del ángulo de tiro θ₀
• Resolvemos la ecuación trascendente para calcular el ángulo θ_m=40.4° que hace que el alcance sea máximo

v0=40; %velocidad inicial 
b=0.000625*9.8; %coeficiente
f=@(x) 4*9.8^2*(cos(x)^2-sin(x)^2)+9.8*b*v0^2*(cos(x)^2*sin(x)-6*sin(x)^3+
4*log(tan(x/2+pi/4))*cos(x)^4)+b^2*v0^4*(-sin(x)^2*cos(x)^2-2*sin(x)^4+
log(tan(x/2+pi/4))*sin(x)*cos(x)^4);
angMax=fzero(f,[0,pi/2])*180/pi;
disp(angMax)
angIni=5:0.5:80;
xMax=zeros(1,length(angIni));
g=@(x) 2*sqrt(2)*v0^2*sin(x)*cos(x)/sqrt(2*9.8^2+3*9.8*b*v0^2*sin(x)+
b^2*v0^4*sin(x)^2+2*9.8*b*v0^2*log(tan(x/2+pi/4))*cos(x)^2+
b^2*v0^4*log(tan(x/2+pi/4))*cos(x)^2*sin(x));
i=1;
for th_0=angIni*pi/180
    xMax(i)=g(th_0);
    i=i+1;
end
plot(angIni, xMax)
maximo=g(angMax*pi/180);
line([angMax, angMax],[0,maximo], 'lineStyle','--')
line([0, angMax],[maximo, maximo], 'lineStyle','--')
grid on
xlabel('\theta_0')
ylabel('R')
title('Alcance máximo')

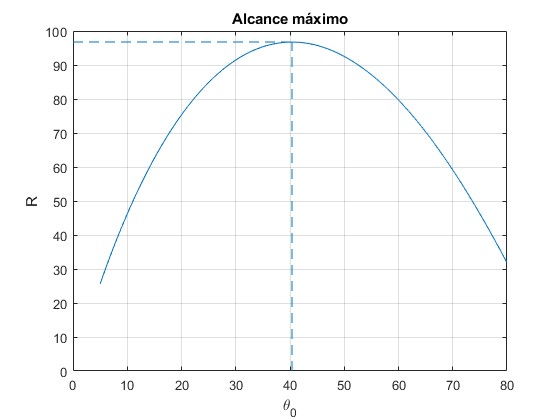
 40.3750

Referencias

R. D. H. Warburton, J. Wang, J. Burgdofer. Analytic Approximations of Projectile Motion with Quadratic Air Resistence. J. Service Science & Management, 2010,3:98-105

Erlichson H. Maximum projectile range with drag and lift, with particular application to golf. Am. J. Phys. 51 (4) April 1983, pp. 357-362.

Warburton R. D. H. , Wang J., Analysis of asymptotic projectile motion with air resistance using Lambert W function. Am. J. Phys. 72 (11) November 2004, pp. 1404-1407

Brancazio P. J. Looking into Chapman's homer: The physics of judging a fly ball. Am. J. Phys. 53 (9) September 1985, pp. 849-855.

Peter S Chudinov. Approximate Analytical Description of the Projectile Motion with a Quadratic Drag Force. Athens Journal of Sciences- Volume 1, Issue 2 – Pages 97-106

Pirooz Mohazzabi. When Does Air Resistance Become Significant in Projectile Motion?. The Physics Teacher. Vol. 56, March 2018. pp. 168-169

John L. Bradshaw. Projectile motion with quadratic drag. Am. J. Phys.91 (4), April 2023, pp. 258-263