Variación de la presión con la altura

En una atmósfera isotérmica, la variación de la presión en función de la altitud x está dada por la ley de Laplace.

${\displaystyle p=p_0\exp \left(\frac{-Mg}{RT}x\right)}$

• p₀ es la presión de la atmósfera a nivel del mar
• M es el peso molecular del aire 28.8 g/mol=0.0288 kg/mol
• g es la aceleración de la gravedad
• R=8.3143 J/(K·mol) es la constante de los gases
• T es la temperatura de la atmósfera en K

Aunque la atmósfera no es isotérmica, la variación de presión con la altura se puede aproximar a una exponencial decreciente, para una temperatura efectiva de 254 K.

${\displaystyle p=p_0\exp \left(\frac{-0.0288·9.8}{8.3143·254}x\right)=P_0\exp \left(\frac{-x}{7482.2}\right)}$

donde p₀= 1 atm es la presión a nivel del mar. La presión a una altura de x=10000 m es de solamente 0.26 atm.

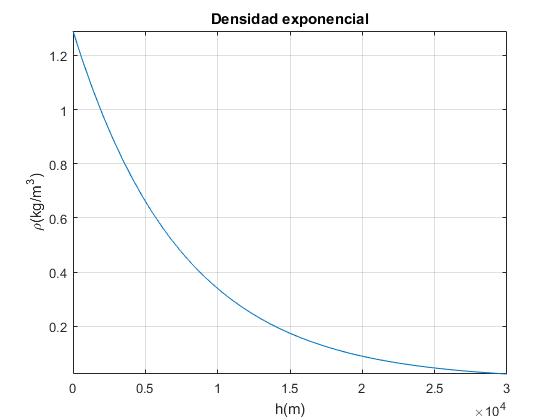
Suponiendo que el aire se comporta como un gas ideal, su densidad varía con la altura de la misma forma que la presión, ρ=ρ₀exp(-x/λ). La densidad del aire al nivel del mar es ρ₀=1.29 kg/m³ y la constante λ=7482.2 m

f=@(x) 1.29*exp(-x/7482.2);
fplot(f,[0,30000])
grid on
xlabel('h(m)')
ylabel('\rho(kg/m^3)')
title('Densidad exponencial')

Ecuación del movimiento

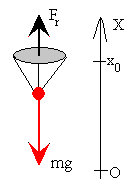
Las fuerzas que actúan sobre el paracaidista son el peso mg que suponemos constante y la fuerza de rozamiento proporcional al cuadrado de la velocidad

${\displaystyle m\frac{dv}{dt}=-mg+\frac{\rho A\delta }{2}{v}^2}$

• ρ es la densidad del aire que cambia con la altura x.
• A es el área de la sección transversal frontal expuesta al aire,
• δ es un coeficiente que depende de la forma del objeto

La ecuación del movimiento es

${\displaystyle m\frac{dv}{dt}=-mg+k_0{v}^2\exp \left(\frac{-x}{\lambda }\right)}$

Ques se resuelve por procedimientos numéricos con las siguientes condiciones iniciales: t=0, x=x₀, (dx/dt)=0

Escribimos esta ecuación de forma alternativa

${\displaystyle mv\frac{dv}{dx}=-mg+k_0{v}^2\exp \left(\frac{-x}{\lambda }\right)}$

Donde k₀ es el valor de la constante de proporcionalidad de la fuerza de rozamiento, al nivel del mar, donde la densidad es ρ₀.

Esta ecuación admite una solución analítica en términos de la función integral exponencial Ei(x). El programa interactivo la resuelve por procedimientos numéricos.

Máxima velocidad alcanzada por el paracaidista.

Observamos que el paracaidista va incrementando su velocidad a medida que cae, alcanzando un máximo y luego, la velocidad disminuye hasta que llega al suelo.

Cuando se alcanza la máxima velocidad dv/dx=0. La relación entre la velocidad máxima v_m y la altura x_m a la que se produce es

${\displaystyle \frac{mg}{k_0}=v_m^2\exp (\frac{-x_m}{\lambda })}$

donde v_l es la velocidad límite que alcanzaría un paracaidista en una atmósfera uniforme.

${\displaystyle v_l=\sqrt{\frac{mg}{k_0}}}$

Se puede calcular x_m, por procedimientos numéricos si disponemos de la solución analítica v=v(x) que por su complejidad omitimos en esta página.

• Masa del paracaidista de m=72 kg,
• Área del paracaídas A=0.6 m²
• El paracaidista parte del reposo desde la posición x₀=30000 m

La velocidad límite v_l que alcanzaría el paracaidista en una atmósfera uniforme es

${\displaystyle v_l=\sqrt{\frac{mg}{k_0}}\text{,}{k}_0=\frac{1.29·A·0.8}{2}}$

v_l=47.7 m/s

Observamos que a la altura de x_m=23996 m se alcanza la máxima velocidad. De la ecuación que relaciona x_m y v_m obtenemos v_m.

${\displaystyle v_l^2=v_m^2\exp \left(\frac{-x_m}{\lambda }\right)\text{,}\text{47}{\text{.7}}^{\text{2}}=v_m^2\exp \left(\frac{-23996}{7482.2}\right)}$

v_m=237.3 m/s

Solución con MATLAB

Escribimos un script en el que se realicen las siguientes tareas:

1. Establezca

• La masa del paracaidista, m
• El área del paracaidas, A
• El paracaidista parte del reposo desde una altura h

2. Resuelva la ecuación diferencial de segundo orden mediante el comado ode45

3. Detenga el proceso de integración cuando llegue al suelo y muestre el valor de la velocidad final

4. Represente la altura x en el eje horizontal y la velocidad v en el eje vertical

Ejemplo: m=72 kg, A=0.6 m², h=30 km=30 000 m

Tenemos que resolver una ecuación diferencial de segundo orden o bien, el sistema de dos ecuaciones diferenciales de primer orden.

Definimos las funciones a integrar en el vector columna, x(1) representará los sucesivos valores de la variable x y x(2) representará a la variable v. El mismo criterio se empleará para determinar el vector x0 de las condiciones iniciales.

f=@(t,x)[x(2); -9.8+(k*x(2)*x(2)/m)*exp(-x(1)/lambda)]; 

En primer lugar, definimos la función detener que detiene el proceso de integración numérica cuando el paracaidista llega al suelo y que le pasaremos a la función ode45 que realiza la integración numérica

function [detect,stopint,direction]=detener(t,x)
% Determina el instante cuando pasa por la altura cero y detiene la integración
    detect=x(1); % Detecta cuando llega al suelo
    stopint=1; % Detiene la integración
    direction=0; % No tiene interés
end

En el script creamos la estructura opts mediante la llamada a la función odeset de MATLAB

function paracaidista
    m=72; %masa
    A=0.6; %área del paracaidas
    k=1.29*A*0.8/2;
    lambda=7482.2;
    
    f=@(t,x)[x(2); -9.8+(k*x(2)*x(2)/m)*exp(-x(1)/lambda)]; 
    opts=odeset('events',@detener);
    [~,x, ~,xe]=ode45(f,[0 inf],[30000,0],opts); 
    plot(x(:,1),-x(:,2))
    text(0,-xe(2),num2str(-xe(2)))
    grid on
    xlabel('x')
    ylabel('v');
    title('Caída de un paracaidista')

    function [detect,stopint,direction]=detener(~,x)
% Determina el instante cuando pasa por la altura cero y detiene la integración
        detect=x(1); % Detecta cuando llega al suelo
        stopint=1; % Detiene la integración
        direction=0; % No tiene interés
    end
end

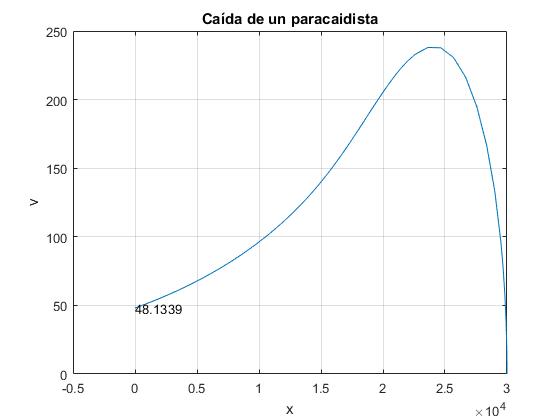
Observamos que la velocidad del paracidista al llegar al suelo es algo mayor que la que tendría en una atmósfera uniforme, v_l=47.7 m/s

A partir del vector velocidad x(:,2), determinamos la velocidad máxima v_m, la altura x_m a la que se alcanza y el instante t_m

[vmax nmax]=max(-x(:,2))
vmax =  238.0084
nmax =    44
>> x(nmax,1)
ans =   2.3620e+04
>> t(nmax)
ans =   40.5828

Velocidad límite

Cuando se alcanza la velocidad máxima, dv/dx=0, el peso y la fuerza de rozamiento se igualan, se alcanza la velocidad límite. Pero esta velocidad límite v no es constante si no que cambia a medida que desciende el paracaidista, debido a que la densidad del aire se incrementa al disminuir la altura

${\displaystyle -mg+k_0{v}^2\exp \left(\frac{-x}{\lambda }\right)=0}$

Despejamos v=dx/dt y tomamos la raíz negativa

${\displaystyle \frac{dx}{dt}=-v_l\exp \left(\frac{x}{2\lambda }\right)}$

La velocidad límite es una función exponencial de la altura x

Representamos la altura x del paracaidista en función del tiempo t, resolviendo la ecuación diferencial como en el script anterior. Representamos en la misma gráfica la altura x del paracaidista en función del tiempo t a partir del instante en el que alcanza la altura máxima, suponiendo que a partir de ese momento, el peso se equilibra con la fuerza de rozamiento

Integramos la ecuación diferencial sabiendo que en el instante t=t_m el paracaidista se encuentra a la altura x=x_m

${\displaystyle \begin{array}{l}{\displaystyle \underset{x_m}{\overset{x}{\int }}\exp \left(\frac{-x}{2\lambda }\right)}dx=-v_l(t-t_m)\\ \exp \left(\frac{-x}{2\lambda }\right)-\exp \left(\frac{-x_m}{2\lambda }\right)=\frac{v_l}{2\lambda }(t-t_m)\end{array}}$

function paracaidista_1
    m=72; %masa
    A=0.6; %área del paracaidas
    k=1.29*A*0.8/2;
    lambda=7482.2;
    
    f=@(t,x) [x(2); -9.8+(k*x(2)*x(2)/m)*exp(-x(1)/lambda)]; 
    opts=odeset('events',@detener);
    [t,x]=ode45(f,[0 inf],[30000,0],opts);
    
    [~,nmax]=max(-x(:,2));
    xlim=-2*lambda*log(exp(-x(nmax,1)/(2*lambda))+sqrt(m*9.8/k)*
(t(nmax:end)-t(nmax))/(2*lambda));
    hold on
    plot(t,x(:,1))
    plot(t(nmax:end),xlim);
    hold off
    legend('ecuación diferencial','velocidad límite')
    grid on
    xlabel('t')
    ylabel('x');
    title('Caída de un paracaidista')

    function [detect,stopint,direction]=detener(~,x)
% Determina el instante cuando pasa por la altura cero y detiene la integración
        detect=x(1); % Detecta cuando llega al suelo
        stopint=1; % Detiene la integración
        direction=0; % No tiene interés
    end
end

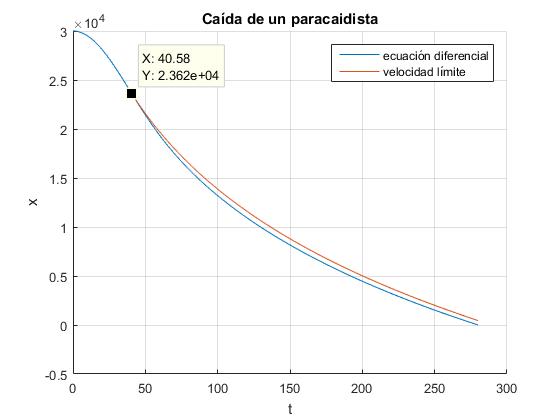
A partir del instante t_m=40.58 s, coinciden bastante, las alturas del paracaidista calculadas resolviendo la ecuación diferencial del movimiento, o suponiendo que el paracaidista ha alcanzado la velocidad límite. Más abajo, en la simulación de este problema, la flecha negra al lado del paracaidista, de longitud constante, representa el peso, la flecha azul que va creciendo a medida que el paracaidista desciende es la fuerza de rozamiento. A partir del momento en el que se alcanza la velocidad máxima, ambas flechas son aparentemente iguales y opuestas.

Actividades

Se introduce

• La masa m del paracaidista en el control titulado Masa
• El área del paracaídas en el control titulado Área
• La altura (en km) desde la que se lanza el paracaidista, actuando en el control titulado Altura.

Se pulsa el botón titulado Nuevo

El paracaidista abre el paracaídas desde la posición de partida.

En la parte izquierda, se representa la presión del aire en función de la altura, de acuerdo con el modelo de atmósfera isoterma.

A continuación, observamos el movimiento del paracaidista sobre un fondo de color que representa la presión en función de la altura en una escala de intensidades de color rojo. Al color blanco, le corresponde la presión nula, y al color rojo, la presión a nivel del mar.

Finalmente, en la parte derecha, se representa la velocidad del paracaidista en función de la altura. En realidad, se representa

• En el eje horizontal 1-x/x₀, donde x₀ es la altura de lanzamiento

• En el eje vertical v/v_l, donde v_l es la velocidad límite constante que alcanza el paracaidista en la atmósfera uniforme.

Observamos que el paracaidista va incrementando su velocidad a medida que cae, alcanzando un máximo. La velocidad disminuye y alcanza un valor próximo a v_l cuando llega al suelo, en la gráfica al valor v/v_l=1.

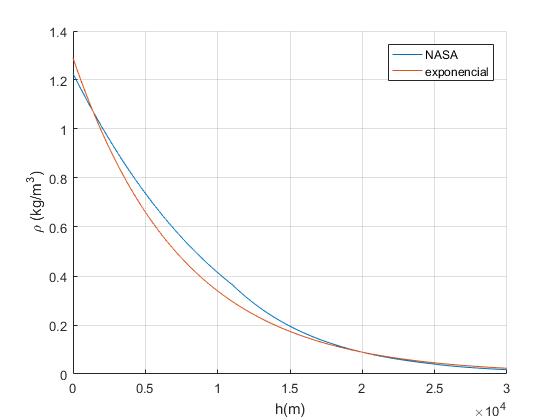
Modelo de atmósfera de la NASA

En la página web https://www.grc.nasa.gov/www/k-12/rocket/atmosmet.html la NASA publica el siguiente modelo de atmósfera. La presión p se proporciona en KPa, la temperatura T en °C, y la densidad ρ en kg/m³

${\displaystyle \begin{array}{l}h>25000\{\begin{array}{l}T=-131.21+0.00299·h\\ p=2.488·{\left(\frac{T+273.1}{216.6}\right)}^{-11.388}\end{array}\\ 11000<h<25000\{\begin{array}{l}T=-56.46\\ p=22.65·\exp \left(1.73-0.000157·h\right)\end{array}\\ h<11000\{\begin{array}{l}T=15.04-0.00649·h\\ p=101.29·{\left(\frac{T+273.1}{288.08}\right)}^{5.256}\end{array}\\ \rho =\frac{p}{0.2869·(T+273.1)}\end{array}}$

Definimos las función densidad_atmosfera_nasa, que proporciona el dato de la densidad ρ, cuando se le pasa la altura h

function rho=densidad_atmosfera_nasa(h)
    if h<11000
        T=15.04-0.00649*h;
        p=101.29*((T+273.1)/288.08)^5.256;
    elseif h>25000
        T=-131.21+0.00299*h;
        p=2.488*((T+273.1)/216.6)^-11.388;
    else
        T=-56.46+h*0;
        p=22.65*exp(1.73-0.000157*h);
    end
    rho=p/(0.2869*(T+273.1));
end

Creamos un script para representar la densidad ρ en función de la altura h y la comparamos con el modelo de atmósfera cuya densidad decrece exponecialmente con la altura, que estudiamos al principio de esta página

function paracaidista_3
    h=0:100:30000;
    densidad=zeros(1,length(h));
    i=0;
    for z=h
        i=i+1;
        densidad(i)=densidad_atmosfera_nasa(z);
    end   
    r=1.29*exp(-h/7482.2);
    hold on
    plot(h,densidad);
    plot(h,r);
    hold off
    grid on
    legend('NASA','exponencial')
    xlabel('h(m)')
    ylabel('\rho (kg/m^3)')
    
    function rho=densidad_atmosfera_nasa(h)
        if h<11000
            T=15.04-0.00649*h;
            p=101.29*((T+273.1)/288.08)^5.256;
        elseif h>25000
            T=-131.21+0.00299*h;
            p=2.488*((T+273.1)/216.6)^-11.388;
        else
            T=-56.46+h*0;
            p=22.65*exp(1.73-0.000157*h);
        end
        rho=p/(0.2869*(T+273.1));
    end
end

Variación de la gravedad con la altura

${\displaystyle g=G\frac{M}{{(R+h)}^2}}$

Como podemos apreciar, la gravedad g cambia ligeramente con la altura h. La constante G=6.67·10^-11, la masa de la Tierra M=5.98·10²⁴ y el radio de la Tierra R=6.37·10⁶. Todas las magnitudes expresadas en el Sistema Internacional de Unidades. Calculamos g para h=0 y para h=30 000 m

>> 6.67e-11*5.98e24/(6.37e6)^2
ans =    9.8299
>> 6.67e-11*5.98e24/(6.37e6+30000)^2
ans =    9.7379

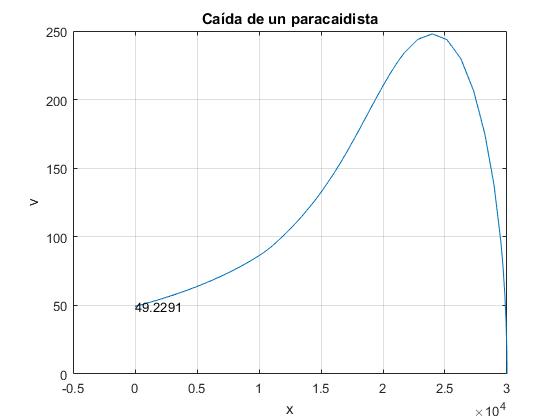
Ecuación diferencial del movimiento

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-mg+\frac{\rho A\delta }{2}{v}^2\\ \frac{d^{2}x}{d{t}^2}=-\frac{GM}{{(R+x)}^2}+\frac{A\delta }{2m}\rho (x){\left(\frac{dx}{dt}\right)}^2\end{array}}$

Con los mismos datos que en la sección previa, vemos que la velocidad final es algo superior a la calculada para una atmósfera cuya densidad decrece exponencialmente con la altura, y la aceleración de la gravedad se supone constante

function paracaidista_2
    m=72; %masa
    A=0.6; %área del paracaidas
    delta=0.8; %coeficiente de forma
    
    f=@(t,x)[x(2); -3.9820e+14/(6.375e6+x(1))^2+
0.5*densidad_atmosfera_nasa(x(1))*delta*A*x(2)^2/m]; 
    opts=odeset('events',@detener);
    [~,x,~,xe]=ode45(f,[0, inf],[30000,0],opts);
    
    plot(x(:,1),-x(:,2))
    text(0,-xe(2),num2str(-xe(2)))
    grid on
    xlabel('x')
    ylabel('v');
    title('Caída de un paracaidista')

    function [detect,stopint,direction]=detener(~,x)
% Determina el instante cuando pasa por la altura cero y detiene la integración
        detect=x(1); % Detecta cuando llega al suelo
        stopint=1; % Detiene la integración
        direction=0; % No tiene interés
    end
    function rho=densidad_atmosfera_nasa(h)
        if h<11000
            T=15.04-0.00649*h;
            p=101.29*((T+273.1)/288.08)^5.256;
        elseif h>25000
            T=-131.21+0.00299*h;
            p=2.488*((T+273.1)/216.6)^-11.388;
        else
            T=-56.46+h*0;
            p=22.65*exp(1.73-0.000157*h);
        end
        rho=p/(0.2869*(T+273.1));
    end
end

Movimiento en dos dimensiones

Vamos a analizar el movimiento de un proyectil disparado con velocidad v₀ haciendo un ángulo θ con la horizontal en una atmósfera no uniforme cuya densidad disminuye exponencialmente con la altura

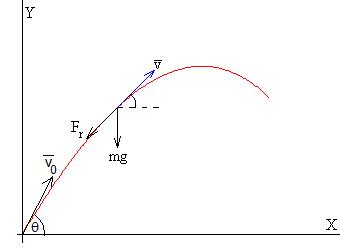
Cuando un cuerpo se mueve en el aire, las fuerzas que actúa son el peso mg y la fuerza de rozamiento $-F(v)\widehat{v}$, opuesta a la dirección de la velocidad

${\displaystyle F(v)=\frac{1}{2}{C}_D\rho v^2}$

• ρ es la densidad del aire
• A es la sección transversal del cuerpo que se mueve
• C_D es un coeficiente que depende de la velocidad

Para objetos pequeños moviéndose en el aire con velocidades menores que 24 m/s, la fuerza de rozamiento es proporcional a la velocidad

Para velocidades mayores la fuerza de rozamiento es proporcional al cuadrado de la velocidad

Para velocidades supersónicas la fuerza de rozamiento es proporcional a la velocidad, pero con un coeficiente diferente.

Escribimos la fuerza de rozamiento de la forma

${\displaystyle F(v)=-v\left(c_1+c_{2}v\right)}$

donde c₁ y c₂ son constantes independientes de la velocidad de proyectil

• Para velocidades por debajo de la velocidad del sonido, c₁=0 y c₂>0
• Para velocidades supersónicas, c₁>0 y c₂=0.

La ecuación del movimiento para un proyectil de masa m moviéndose en la atmósfera es

${\displaystyle \begin{array}{l}m\frac{d^2\overrightarrow{r}}{d{t}^2}=-mg\widehat{j}-\left(c_1+c_{2}v\right)\frac{d\overrightarrow{r}}{dt}\\ \{\begin{array}{l}\frac{d^{2}x}{d{t}^2}=-\frac{c_1+c_{2}v}{m}\frac{dx}{dt}\\ \frac{d^{2}y}{d{t}^2}=-g-\frac{c_1+c_{2}v}{m}\frac{dy}{dt}\end{array}\end{array}}$

La fuerza de rozamiento es proporcional a la densidad que es a su vez, proporcional a la presión, que para una atmósfera isoterma es

${\displaystyle p=p_0\exp \left(-\frac{Mg}{RT}y\right)=p_0\exp \left(-\frac{y}{H}\right)}$

donde H=7.4621 km a la temperatura efectiva de T=254 K

${\displaystyle c_1=c_{10}\exp \left(-\frac{y}{H}\right),c_2=c_{20}\exp \left(-\frac{y}{H}\right)}$

Definimos unidades adimensionales

${\displaystyle \begin{array}{l}\xi =\frac{x}{H},\zeta =\frac{y}{H},\tau =\sqrt{\frac{g}{H}}t\\ {\gamma }_1=\frac{c_{10}}{m}\sqrt{\frac{H}{g}},{\gamma }_2=\frac{c_{20}}{m}H\end{array}}$

Las ecuaciones del movimiento se transforman

${\displaystyle \begin{array}{l}v=\sqrt{{\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2}=\sqrt{gH}\sqrt{{\left(\frac{d\xi }{d\tau }\right)}^2+{\left(\frac{d\zeta }{d\tau }\right)}^2}=V\sqrt{gH}\\ \frac{c_{10}+c_{20}v}{m}=\frac{m{\gamma }_1\sqrt{\frac{g}{H}}+{\gamma }_2\frac{m}{H}V\sqrt{gH}}{m}=\left({\gamma }_1+{\gamma }_{2}V\right)\sqrt{\frac{g}{H}}\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{d^2\xi }{d{\tau }^2}=-\left({\gamma }_1+{\gamma }_{2}V\right)e^{-\zeta }\frac{d\xi }{d\tau }\\ \frac{d^2\zeta }{d{\tau }^2}=-1-\left({\gamma }_1+{\gamma }_{2}V\right)e^{-\zeta }\frac{d\zeta }{d\tau }\end{array}\\ V=\sqrt{{\left(\frac{d\xi }{d\tau }\right)}^2+{\left(\frac{d\zeta }{d\tau }\right)}^2}\end{array}}$

Atmósfera uniforme

En una atmósfera uniforme la densidad es constante, el término exp(-ζ) desaparece de las ecuaciones del movimiento

${\displaystyle \{\begin{array}{l}\frac{d^2\xi }{d{\tau }^2}=-\left({\gamma }_1+{\gamma }_{2}V\right)\frac{d\xi }{d\tau }\\ \frac{d^2\zeta }{d{\tau }^2}=-1-\left({\gamma }_1+{\gamma }_{2}V\right)\frac{d\zeta }{d\tau }\end{array}}$

Tiro parabólico, sin atmósfera

${\displaystyle \begin{array}{l}\{\begin{array}{l}x=v_0\cos \theta ·t\\ y=v_0\sin \theta ·t-\frac{1}{2}g{t}^2\end{array}\\ \{\begin{array}{l}\xi H=V_0\sqrt{gH}\cos \theta ·\tau \sqrt{\frac{H}{g}}\\ \zeta H=V_0\sqrt{gH}\sin \theta \tau \sqrt{\frac{H}{g}}-\frac{1}{2}g{\tau }^2\frac{H}{g}\end{array}\\ \{\begin{array}{l}\xi =V_0\cos \theta ·\tau \\ \zeta =V_0\sin \theta ·\tau -\frac{1}{2}{\tau }^2\end{array}\end{array}}$

Resultados

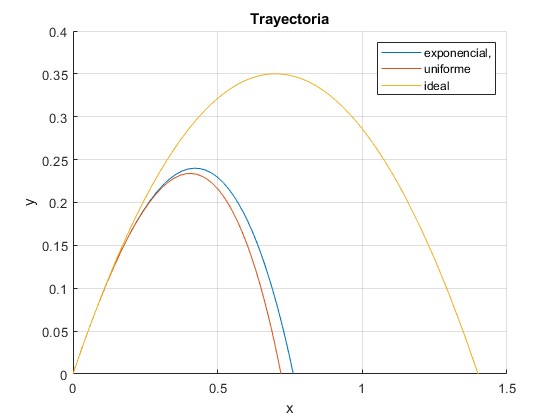
• Disparamos un proyectil con velocidad v₀=320 m/s, (por debajo de la velocidad del sonido), haciendo un ángulo de θ= 45° con la horizontal

En este caso, γ₁=0 y γ₂=1

function atm_exp_5
    g_1=0;
    g_2=1;
    H=7462.1;
    V0=320/sqrt(9.8*H); %velocidad de disparo
    th=pi/4; %ángulo de tiro
    hold on
    %atmósfera exponencial
    f=@(t,x)[x(2); -(g_1+g_2*sqrt(x(2)^2+x(4)^2))*exp(-x(3))*x(2); x(4); 
-1-(g_1+g_2*sqrt(x(2)^2+x(4)^2))*exp(-x(3))*x(4)];
    opts=odeset('events',@detener);
    [~,x]=ode45(f,[0,2*V0*sin(th)],[0,V0*cos(th),0 V0*sin(th)],opts);
     plot(x(:,1), x(:,3))
    %atmósfera uniforme
    f=@(t,x)[x(2); -(g_1+g_2*sqrt(x(2)^2+x(4)^2))*x(2); x(4); 
-1-(g_1+g_2*sqrt(x(2)^2+x(4)^2))*x(4)];
    opts=odeset('events',@detener);
    [~,x]=ode45(f,[0,2*V0*sin(th)],[0,V0*cos(th),0 V0*sin(th)],opts);
    plot(x(:,1), x(:,3))
    %tiro parabólico, sin rozamiento    
    fplot(@(t) V0*cos(th)*t, @(t) V0*sin(th)*t-t.^2/2,[0,2*V0*sin(th)])
    hold off
    grid on
    legend('exponencial,','uniforme','ideal')
    xlabel('x')
    ylabel('y')
    title('Trayectoria')

    function [value,isterminal,direction]=detener(~,x)
       %x(1) es  x, x(3) es y
        value=x(3);
        isterminal=1; %1 detiene la integración   
        direction=-1; % 1 crece, -1 decrece, 0 no importa
    end
end



Representamos el alcance R en función del ángulo de tiro θ.

function atm_exp_7
    g_1=0;
    g_2=1;
    H=7462.1;
    V0=320/sqrt(9.8*H); %velocidad de disparo
    angulos=(30:60)*pi/180;
    R1=zeros(1,length(angulos));
    R2=zeros(1,length(angulos));
    hold on
    k=1;
    opts=odeset('events',@detener);
    for th=angulos
    %atmósfera exponencial
        f=@(t,x)[x(2); -(g_1+g_2*sqrt(x(2)^2+x(4)^2))*exp(-x(3))*x(2); x(4); 
-1-(g_1+g_2*sqrt(x(2)^2+x(4)^2))*exp(-x(3))*x(4)];
        [~,x]=ode45(f,[0,V0*sin(th)],[0,V0*cos(th),0 V0*sin(th)],opts);
        R1(k)=x(end,1);
    %atmósfera uniforme
        f=@(t,x)[x(2); -(g_1+g_2*sqrt(x(2)^2+x(4)^2))*x(2); x(4); 
-1-(g_1+g_2*sqrt(x(2)^2+x(4)^2))*x(4)];
        [~,x]=ode45(f,[0,V0*sin(th)],[0,V0*cos(th),0 V0*sin(th)],opts);
        R2(k)=x(end,1);
        k=k+1;
    end
    plot(angulos,R1,'ro','markersize',3,'markerfacecolor','r')
    plot(angulos,R2,'bo','markersize',3,'markerfacecolor','b')
    hold off
    grid on
    set(gca,'XTick',pi/6:pi/12:pi/3)
    set(gca,'XTickLabel',{'\pi/6','\pi/4','\pi/3'})
    legend('exponencial,','uniforme','location','best')
    ylabel('R')
    xlabel('\theta')
    title('Alcance')

    function [value,isterminal,direction]=detener(~,x)
       %x(1) es  x, x(3) es y
        value=x(3);
        isterminal=1; %1 detiene la integración    
        direction=-1; % 1 crece, -1 decrece, 0 no importa
    end
end



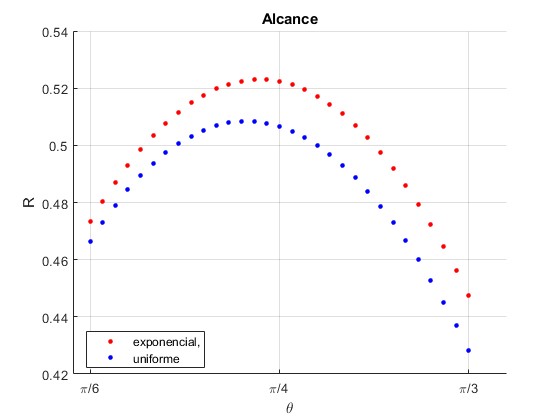
El alcance máximo se produce para ángulos de tiro menores de π/4, (45°)

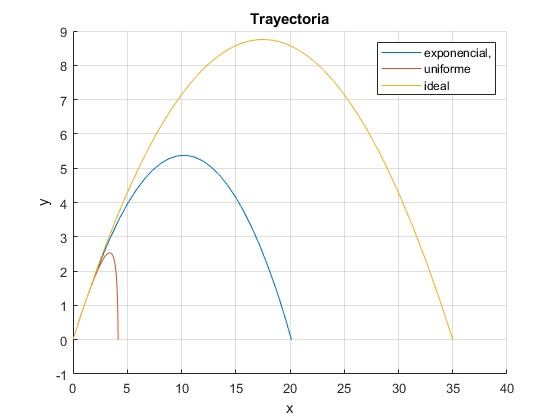
• Disparamos un proyectil con velocidad v₀=5·320 m/s, (por encima de la velocidad del sonido), haciendo un ángulo de θ= 45° con la horizontal

En este caso, γ₁=1 y γ₂=0

function atm_exp_6
    g_1=1;
    g_2=0;
    H=7462.1;
    V0=5*320/sqrt(9.8*H);
    th=pi/4; %ángulo de tiro
    hold on
    f=@(t,x)[x(2); -(g_1+g_2*sqrt(x(2)^2+x(4)^2))*exp(-x(3))*x(2); x(4); 
-1-(g_1+g_2*sqrt(x(2)^2+x(4)^2))*exp(-x(3))*x(4)];
    opts=odeset('events',@detener);
    [~,x]=ode45(f,[0,2*V0*sin(th)],[0,V0*cos(th),0 V0*sin(th)],opts);
     plot(x(:,1), x(:,3))
    %atmósfera uniforme
    f=@(t,x)[x(2); -(g_1+g_2*sqrt(x(2)^2+x(4)^2))*x(2); x(4); 
-1-(g_1+g_2*sqrt(x(2)^2+x(4)^2))*x(4)];
    opts=odeset('events',@detener);
    [~,x]=ode45(f,[0,2*V0*sin(th)],[0,V0*cos(th),0 V0*sin(th)],opts);
    plot(x(:,1), x(:,3))
    %tiro parabólico, sin rozamiento    
    fplot(@(t) V0*cos(th)*t, @(t) V0*sin(th)*t-t.^2/2,[0,2*V0*sin(th)])
    hold off
    grid on
    legend('exponencial,','uniforme','ideal')
    xlabel('x')
    ylabel('y')
    title('Trayectoria')

    function [value,isterminal,direction]=detener(~,x)
       %x(1) es  x, x(3) es y
        value=x(3);
        isterminal=1; %1 detiene la integración   
        direction=-1; % 1 crece, -1 decrece, 0 no importa
    end
end



Representamos el alcance R en función del ángulo de tiro θ.

function atm_exp_8
    g_1=1;
    g_2=0;
    H=7462.1;
    V0=5*320/sqrt(9.8*H);
    angulos=(30:60)*pi/180;
    R1=zeros(1,length(angulos));
    R2=zeros(1,length(angulos));
    hold on
    opts=odeset('events',@detener);
    k=1;
    for th=angulos
        f=@(t,x)[x(2); -(g_1+g_2*sqrt(x(2)^2+x(4)^2))*exp(-x(3))*x(2); x(4); 
-1-(g_1+g_2*sqrt(x(2)^2+x(4)^2))*exp(-x(3))*x(4)];
        [~,x]=ode45(f,[0,2*V0*sin(th)],[0,V0*cos(th),0 V0*sin(th)],opts);
        R1(k)=x(end,1);
        %atmósfera uniforme
        f=@(t,x)[x(2); -(g_1+g_2*sqrt(x(2)^2+x(4)^2))*x(2); x(4); 
-1-(g_1+g_2*sqrt(x(2)^2+x(4)^2))*x(4)];
        [~,x]=ode45(f,[0,2*V0*sin(th)],[0,V0*cos(th),0 V0*sin(th)],opts);
        R2(k)=x(end,1);
        k=k+1;
    end
    plot(angulos,R1,'ro','markersize',3,'markerfacecolor','r')
    plot(angulos,R2,'bo','markersize',3,'markerfacecolor','b')
    hold off
    grid on
    set(gca,'XTick',pi/6:pi/12:pi/3)
    set(gca,'XTickLabel',{'\pi/6','\pi/4','\pi/3'})
    legend('exponencial,','uniforme','location','best')
    ylabel('R')
    xlabel('\theta')
    title('Trayectoria')

    function [value,isterminal,direction]=detener(~,x)
       %x(1) es  x, x(3) es y
        value=x(3);
        isterminal=1; %1 detiene la integración   
        direction=-1; % 1 crece, -1 decrece, 0 no importa
    end
end



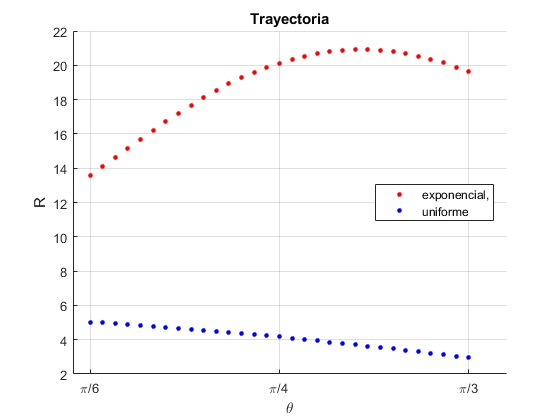
El alcance máximo, para un proyectil que se mueve en la atmósfera no uniforme, se produce para ángulos de tiro mayores de π/4, (45°)

Referencias

Mohazzabi P. High-altitude free fall. Am. J. Phys. 64 (10) October 1996, pp. 1242-1246

Pirooz Mohazzabi, Jennene C. Fields. High-altitude projectile motion. Can. J. Phys. 82: 197–204 (2004)