Fuerza entre dos esferas conductoras

Cuando se comienza el estudio del electromagnetismo, siempre se menciona la ley de Coulomb de atracción o repulsión entre cargas puntuales q₁ y q₂

En realidad las cargas no son puntuales sino esferas conductoras de radio R. Ahora bien, cuando dos esferas conductoras de la misma carga y radio están cercanas, se produce una redistribución de las cargas debido a la influencia mutua electrostática, las esferas se polarizan y las cargas del mismo signo tienden a alejarse lo máximo posible, la fuerza de repulsión entre las esferas será menor que la correspondiente a dos cargas puntuales iguales y del mismo signo.

Si las esferas conductoras tienen carga de signos opuestos, las cargas tienden a acercarse, dando lugar a una fuerza de atracción mayor que la correspondiente a dos cargas iguales y de signo contrario.

En esta página, vamos a medir la fuerza de repulsión F entre dos esferas conductoras del mismo radio R con la misma carga Q y del mismo signo. Vamos a comprobar que la fuerza difiere de la ley de Coulomb de atracción o repulsión entre cargas puntuales q₁ y q₂

$F_{c} = \frac{1}{4 π ε_{0}} \frac{q_{1} q_{2}}{d^{2}}$

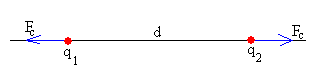
Donde d es la separación entre las cargas puntuales.

Método de las imágenes

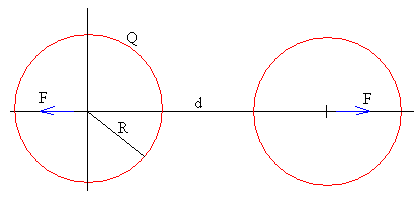
Aplicaremos el método de las imágenes a dos esferas del mismo radio R y de la misma carga Q, separadas entre sus centros una distancia d>2R. Situaremos el origen en el centro de la primera esfera.

La simetría del problema nos permite reemplazar las esferas cargadas por dos sucesiones idénticas de cargas puntuales q₀, q₁…q_n… situadas en la línea que une los centros en las posiciones x₀, x₁…x_n … y d-x₀, d-x₁…d-x_n …, respectivamente. Nos fijaremos exclusivamente en la primera esfera cuyo centro está en el origen.

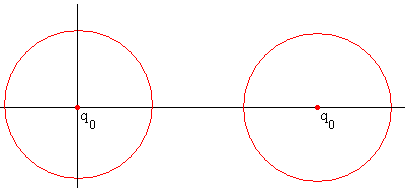
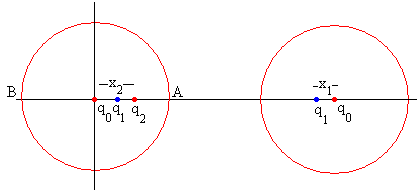
Colocamos una carga q₀ en el centro de la primera esfera, en el origen x₀=0. La superficie de la primera esfera de radio R es equipotencial. Colocamos una carga idéntica q₀en el centro de la segunda esfera. La superficie de la primera esfera deja de ser equipotencial.

Colocamos una carga q₁ a una distancia x₁ del centro de la primera esfera.

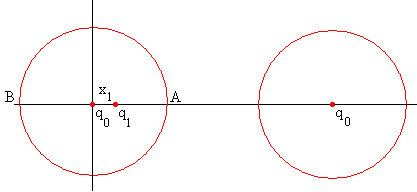
El potencial producido por la carga q₀ situada en el centro de la segunda esfera y por la carga adicional q₁ debe cancelarse en la superficie de la primera esfera, para que siga siendo equipotencial. El potencial en el punto A (R, 0) y B(-R, 0) producido por ambas cargas debe ser cero

$\begin{array}{l} \frac{1}{4 π ε_{0}} \frac{q_{0}}{d - R} + \frac{1}{4 π ε_{0}} \frac{q_{1}}{R - x_{1}} = 0 \\ \frac{1}{4 π ε_{0}} \frac{q_{0}}{d + R} + \frac{1}{4 π ε_{0}} \frac{q_{1}}{R + x_{1}} = 0 \end{array}$

Tenemos un sistema de dos ecuaciones con dos incógnitas cuya solución es

$x_{1} = \frac{R^{2}}{d} q_{1} = - q_{0} \frac{R}{d} = - q_{0} β$

Si colocamos una carga q₁ en la posición d-x₁, la superficie de la primera esfera deja de ser equipotencial.
Colocamos una carga q₂ en la posición x₂, tal como se muestra en la figura.

El potencial producido por la carga q₁ situada en la segunda esfera y por la carga adicional q₂ debe cancelarse en la superficie de la primera esfera, para que siga siendo equipotencial. El potencial en el punto A (R, 0) y B(-R, 0) producido por ambas cargas debe ser cero

$\begin{array}{l} \frac{q_{1}}{d - R - x_{1}} + \frac{q_{2}}{R - x_{2}} = 0 \\ \frac{q_{1}}{d + R - x_{1}} + \frac{q_{2}}{R + x_{2}} = 0 \end{array}$

Primero eliminamos q₁ y q₂ y despejamos x₂, luego, despejamos q₂ de la primera o de la segunda ecuación

$x_{2} = \frac{R^{2}}{d - x_{1}} q_{2} = - q_{1} \frac{R}{d - x_{1}}$

o bien,

$x_{2} = \frac{R^{2} d}{d^{2} - R^{2}} q_{2} = q_{0} \frac{R^{2}}{d^{2} - R^{2}} = q_{0} \frac{β^{2}}{1 - β^{2}}$

Si colocamos una carga q₂ en la posición d-x₂ la superficie de la primera esfera deja de ser equipotencial.
Colocamos una carga q₃ en la posición x₃, tal como se muestra en la figura.

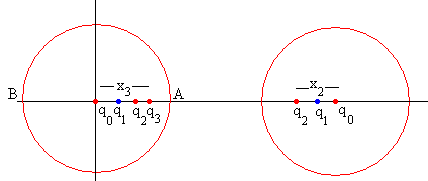
El potencial producido por la carga q₂ situada en la segunda esfera y por la carga adicional q₃ debe cancelarse en la superficie de la primera esfera, para que siga siendo equipotencial. El potencial en el punto A (R, 0) y B(-R, 0) producido por ambas cargas debe ser cero

$\begin{array}{l} \frac{q_{2}}{d - R - x_{2}} + \frac{q_{3}}{R - x_{3}} = 0 \\ \frac{q_{2}}{d + R - x_{2}} + \frac{q_{3}}{R + x_{3}} = 0 \end{array}$

Primero eliminamos q₂ y q₃ y despejamos x₃, luego, despejamos q₃ de la primera o de la segunda ecuación

$x_{3} = \frac{R^{2}}{d - x_{2}} q_{3} = - q_{2} \frac{R}{d - x_{2}}$

o bien,

$x_{3} = \frac{R^{2} (d^{2} - R^{2})}{d (d^{2} - 2 R^{2})} q_{3} = - q_{0} \frac{R^{3}}{d (d^{2} - 2 R^{2})} = - q_{0} \frac{β^{3}}{1 - 2 β^{2}}$

Continuamos es proceso iterativo, obteniendo el valor de la carga imagen q₄ en la posición x₄.

$x_{4} = \frac{R^{2} d (d^{2} - 2 R^{2})}{(d^{4} - 3 R^{2} d^{2} + R^{4})} q_{4} = q_{0} \frac{R^{4}}{d^{4} - 3 R^{2} d^{2} + R^{4}} = q_{0} \frac{β^{4}}{1 - 3 β^{2} + β^{4}}$

La carga total de cada esfera es

$Q = q_{0} + q_{1} + ... + q_{n} + ... = \sum_{i = 0}^{\infty} q_{i}$

que es proporcional a q₀

Actividades

Se introduce

La distancia d>2R entre los centros de las esferas tomando como unidad su radio R, en el control titulado Distancia.

Se pulsa el botón titulado Nuevo.

Se trazan las líneas de fuerza y equipotenciales del sistema formado por dos esferas conductoras del mismo radio y con la misma carga.

Distancia:

Fuerza entre las dos esferas conductoras

La fuerza entre las dos esferas es la suma de las fuerzas entre cada par de cargas imagen una carga correspondiente a la primera esfera y la otra correspondiente a la segunda esfera

$F = \frac{1}{4 π ε_{0}} \sum_{i, j = 0}^{\infty} \frac{q_{i} q_{j}}{{(d - x_{j} - x_{i})}^{2}}$

Cálculo aproximado de la fuerza de repulsión entre las dos esferas

Para calcular la fuerza de repulsión entre dos esferas del mismo radio R y la misma carga Q, se emplea el siguiente procedimiento numérico.

El programa interactivo calcula las cargas imágenes q₀…q_n y sus posiciones x₀…..x_n correspondientes a la primera esfera, que son las misma que las de la segunda esfera pero en las posiciones d-x₀…..d-x_n, mediante las relaciones de recurrencia

$x_{n} = \frac{R^{2}}{d - x_{n - 1}} q_{n} = - \frac{R}{d - x_{n - 1}} q_{n - 1} n > 0 x_{0} = 0$

Se calcula la carga inicial q₀ teniendo en cuenta que la carga de cada esfera es Q.

$Q = \sum_{i = 0}^{n} q_{i}$

Se calcula la fuerza entre los dos conjuntos de cargas imágenes

$F_{n} = \frac{1}{4 π ε_{0}} \sum_{i, j = 0}^{n} \frac{q_{i} q_{j}}{{(d - x_{j} - x_{i})}^{2}}$

Se detiene el proceso iterativo cuando el cociente

$\frac{F_{n + 1} - F_{n}}{F_{n}} < ε$

es menor que una cantidad prefijada, cuyo valor tomaremos ε=10^-6.

%esfera de radio R=1
d=3; %distancia entre las esferas d>2
fuerza2=1/d^2;  %fuerza entre cargas puntuales
fuerza1=0;
nCargas=1;
q=zeros(1,10);
x=zeros(1,10);
while(1)
    x(1)=0;
    q(1)=1;
    for i=2:nCargas+1
        x(i)=1/(d-x(i-1));
        q(i)=-q(i-1)/(d-x(i-1));
    end
    q=q/sum(q); %la suma de las cargas es la unidad
    fuerza1=0;
    for i=1:nCargas+1
        for j=1:nCargas+1
            fuerza1=fuerza1+q(i)*q(j)/(d-x(i)-x(j))^2;
        end
    end
    if(abs((fuerza1-fuerza2)/fuerza2)<0.000001) 
        fprintf('La fuerza es %1.5f para la distancia  %1.2f\n',fuerza2, d)
        break;
    end
    fuerza2=fuerza1;
    nCargas=nCargas+1;
end

La fuerza es 0.09444 para la distancia  3.00

La fuerza entre dos cargas puntuales q=1, separadas d=3 es 1/3²=0.1111

Transformamos el script en la función denominada coulomb para calcular la fuerza de repulsión entre las dos esferas cargadas en función de la distancia d entre los centros de las esferas. La función devuelve también, el número de cargas imagen empleadas en el cálculo hasta la precisión deseada

%devuelve la fuerza y el número de cargas imagen
    function [fuerza2,nCargas] =coulomb(d)
    fuerza2=1/d^2;
    fuerza1=0;
    nCargas=1;
    q=zeros(1,1200);
    x=zeros(1,1200);
    while(1)
        x(1)=0;
        q(1)=1;
        for i=2:nCargas+1
            x(i)=1/(d-x(i-1));
            q(i)=-q(i-1)/(d-x(i-1));
        end
        q=q/sum(q);
        fuerza1=0;
        for i=1:nCargas+1
            for j=1:nCargas+1
                fuerza1=fuerza1+q(i)*q(j)/(d-x(i)-x(j))^2;
            end
        end
        if(abs((fuerza1-fuerza2)/fuerza2)<0.000001) 
            break;
        end
        fuerza2=fuerza1;
        nCargas=nCargas+1;
    end
end

Creamos un script que llame a la función coulomb para reproducir las tres primeras columnas (distancia entre los centros de las esferas, d, número de cargas imagen, n, y fuerza de repulsión F_n hasta la precisión deseada) de la tabla I del artículo citado en las referencias

disp(['d',' n. cargas','  fuerza'])
for d=[10:-1:3,2.5:-0.1:2.2, 2*ones(1,4)+1./10.^(1:4)]
    [f,n]=coulomb(d);
    fprintf('%1.4f  %i  %1.6f\n',d,n,f)
end

d     n. cargas  fuerza
10.0000  5  0.009960
9.0000  6  0.012277
8.0000  6  0.015501
7.0000  7  0.020165
6.0000  7  0.027250
5.0000  8  0.038680
4.0000  10  0.058456
3.0000  15  0.094437
2.5000  21  0.121091
2.4000  23  0.127089
2.3000  27  0.133313
2.2000  33  0.139794
2.1000  46  0.146582
2.0100  135  0.152994
2.0010  392  0.153652
2.0001  1126  0.153718

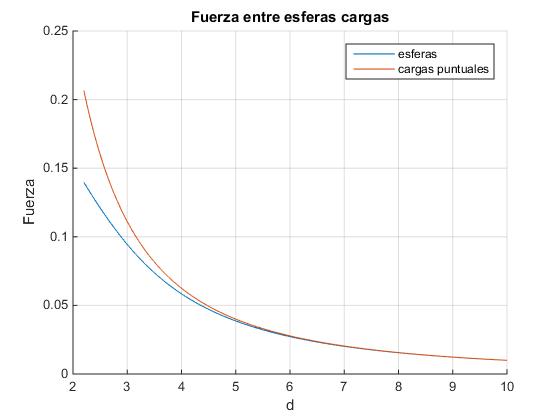
Creamos otro script para representar gráficamente esta fuerza y compararla con la fuerza de repulsión entre dos cargas puntuales (ley de Coulomb) separadas la misma distancia, observando una divergencia notable cuando la separación entre los centros de las esferas d≈2R, cuando las esferas est6aac n casi en contacto la una con la otra

x=2.2:0.05:10;
y=zeros(1,length(x));
for i=1:length(x)
    y(i)=coulomb(x(i));
end
hold on
z=1./x.^2;
plot(x,y,x,z)
grid on
legend('esferas','cargas puntuales')
xlabel('d')
ylabel('Fuerza')
title('Fuerza entre esferas cargas')

El programa interactivo calcula la fuerza F en unidades F_u

$F_{u} = \frac{1}{4 π ε_{0}} \frac{Q^{2}}{R^{2}}$

Actividades

Se introduce

La distancia d>2R entre los centros de las esferas tomando como unidad su radio R, en el control titulado Distancia

Se pulsa el botón titulado Calcula.

Se representa en color azul la fuerza de repulsión entre dos cargas puntuales cuando su separación d varía entre 2.0R y 10.0R.
Se proporciona el valor de la fuerza de repulsión entre dos esferas conductoras iguales cargadas con la misma carga, cuyos centros están separados una distancia d, en unidades F_u y se representa por un punto en la gráfica.

Para volver a empezar a tomar medidas se pulsa el botón titulado Nuevo.

El programa interactivo calcula la fuerza de repulsión entre las dos esferas conductoras para distancias entre sus centros mayores que 2.01R, e indica el número de cargas imagen necesarias para calcularla

Distancia:

Referencias

Slisko J., Brito-Orta R. A., On approximate formulas for the electrostatic force between two conducting spheres. Am. J. Phys. 66 (4) April 1998, pp. 352-355.