Conductor esférico a potencial cero, situado en un campo eléctrico uniforme

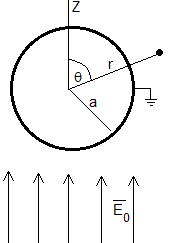
Estudiamos el potencial producido por un conductor esférico de radio a que se mantiene a potencial cero en un campo eléctrico uniforme E₀

El potencial V(r,θ) es

${\displaystyle V(r,\theta )={\displaystyle \sum _{n=0}^{\infty }\left(A_n{r}^n+\frac{B_n}{r^{n+1}}\right)P_n(\cos \theta )}}$

Condiciones de contorno

El potencial en un punto z=rcosθ muy alejado de la esfera de radio a se debe solamente al campo eléctrico uniforme, es V=-E₀rcosθ. Las condiciones de contorno son:

${\displaystyle \{\begin{array}{l}V(\infty ,\theta )=-E_{0}r\cos \theta \\ V(a,\theta )=0\end{array}}$

Potencial eléctrico para r>a

Cuando r es grande los términos B_n/rⁿ⁺¹ tiende a cero, la expresión del potencial será

${\displaystyle -E_{0}r\cos \theta ={\displaystyle \sum _{n=0}^{\infty }{A}_n{r}^n{P}_n(\cos \theta )}}$

Teniendo en cuenta que P₁(cosθ)=cosθ y aplicando las relaciones de ortogonalidad de los polinomios de Legendre. Véase tambien la página titulada Ecuación de Laplace. Coordenadas esféricas

${\displaystyle \begin{array}{l}-E_{0}r\cos \theta ={\displaystyle \sum _{n=0}^{\infty }{A}_n{r}^n{P}_n(\cos \theta )}\\ -E_{0}r{P}_1(\cos \theta )=A_0+{\displaystyle \sum _{n=1}^{\infty }{A}_n{r}^n{P}_n(\cos \theta )}\\ -E_{0}r{\displaystyle \underset{0}{\overset{\pi }{\int }}{P}_1^2(\cos \theta )\sin \theta ·d\theta }={\displaystyle \underset{0}{\overset{\pi }{\int }}\left({\displaystyle \sum _{n=0}^{\infty }{A}_n{r}^n{P}_n(\cos \theta )}\right)}{P}_1(\cos \theta )\sin \theta ·d\theta \\ -E_{0}r{\displaystyle \underset{0}{\overset{\pi }{\int }}{P}_1^2(\cos \theta )\sin \theta ·d\theta }={\displaystyle \sum _{n=0}^{\infty }{A}_n{r}^n{\displaystyle \underset{0}{\overset{\pi }{\int }}{P}_n(\cos \theta )}{P}_1(\cos \theta )\sin \theta ·d\theta }\\ -E_{0}r\frac{2}{2·1+1}=A_{1}r\frac{2}{2·1+1}\end{array}}$

Todos los coeficientes A_n son ceros excepto A₁=-E₀

La expresión del potencial eléctrico es

${\displaystyle V(r,\theta )={\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{r^{n+1}}{P}_n(\cos \theta )}-E_{0}r\cos \theta }$

Superficie de la esfera conductora, r=a

En a superficie de la esfera conductora, V(a, θ)=0. Utilizamos las relaciones de ortogonalidad de los polinomios de Legendre para calcular los coeficientes B_n.

${\displaystyle \begin{array}{l}0={\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{a^{n+1}}{P}_n(\cos \theta )}-E_{0}a{P}_1(\cos \theta )\\ {\displaystyle \underset{0}{\overset{\pi }{\int }}\left({\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{a^{n+1}}{P}_n(\cos \theta )}\right)P_m(\cos \theta )\sin \theta ·d\theta -E_{0}a{\displaystyle \underset{0}{\overset{\pi }{\int }}{P}_1(\cos \theta )P_m(\cos \theta )\sin \theta ·d\theta }=0}\\ {\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{a^{n+1}}{\displaystyle \underset{0}{\overset{\pi }{\int }}{P}_n(\cos \theta )P_m(\cos \theta )\sin \theta ·d\theta -E_{0}a{\displaystyle \underset{0}{\overset{\pi }{\int }}{P}_1(\cos \theta )P_m(\cos \theta )\sin \theta ·d\theta }=0}}\\ \frac{B_m}{a^{m+1}}\frac{2}{2m+1}=\mathrm{0,}{B}_m=\mathrm{0,}m\ne 1\\ \frac{B_1}{a^2}\frac{2}{2·1+1}-E_{0}a\frac{2}{2·1+1}=\mathrm{0,}{B}_1=E_0{a}^3\end{array}}$

Campo eléctrico y potencial

El potencial V(r,θ) es

${\displaystyle V(r,\theta )=\frac{B_1}{r^2}{P}_1(\cos \theta )-E_{0}r\cos \theta =-E_0\left(1-\frac{a^3}{r^3}\right)r\cos \theta }$

Las componentes del campo eléctrico

${\displaystyle \begin{array}{l}{E}_r=-\frac{\partial V}{\partial r}=E_0\left(1+2\frac{a^3}{r^3}\right)\cos \theta \\ E_{\theta }=-\frac{1}{r}\frac{\partial V}{\partial \theta }=-E_0\left(1-\frac{a^3}{r^3}\right)\sin \theta \end{array}}$

En las proximidades de una superficie conductora r=a, el campo eléctrico es perpendicular a la superficie E_θ=0 y su valor es E_n=σ/ε₀. Donde σ es la densidad superficial de carga en C/m². En el caso de una superficie esférica, el campo E_n es el campo en la dirección radial E_r para r=a

${\displaystyle \sigma ={\epsilon }_0{E}_r=3{\epsilon }_0{E}_0\cos \theta }$

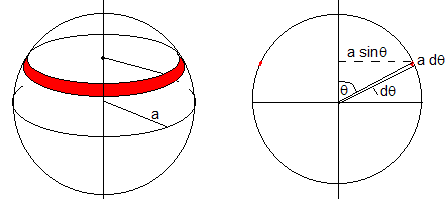
La carga inducida neta q en la esfera conductora se obtiene multiplicando la densidad de carga por el elemento de superficie esférica comprendido entre θ y θ +dθ, sumando para todos los ángulos comprendidos entre 0 y π.

${\displaystyle q={\displaystyle \underset{0}{\overset{\pi }{\int }}\sigma 2\pi a^2\sin \theta d\theta =0}}$

la carga neta q=0 es cero.

Actividades

El programa interactivo muestra las líneas de fuerza y equipotenciales de un campo eléctrico uniforme paralelo al eje X (horizontal) y una esfera conductora conectada a tierra.

Se introduce

• el valor del campo eléctrico E₀, en el control titulado Campo eléctrico.
• el radio a de la esfera se ha fijado en la unidad.

Se pulsa el botón titulado Nuevo

Observamos como se perturba el campo cuando se introduce una esfera conductora en el espacio en el que existe un campo eléctrico uniforme.

Observamos una imagen de la distribución de carga inducida, es decir, de la variación de la densidad de carga σ en función del ángulo θ. Los puntos de color rojo representan las cargas positivas y los azules las cargas negativas.

Al aplicar un campo eléctrico, los portadores de carga negativa de la esfera conductora se mueve en el sentido contrario al campo, hacia la izquierda, dejando la parte derecha del conductor cargada positivamente. Tenemos de este modo un dipolo, formado por una distribución espacial y simétrica de dos cargas iguales y opuestas. La densidad de carga positiva es máxima para θ=0 y la densidad de carga negativa es máxima para θ=π. La densidad de carga es nula para θ=π/2. Como vemos no hay líneas de fuerza que lleguen o salgan de esta posición.

Esférica dieléctrica situada en un campo eléctrico uniforme

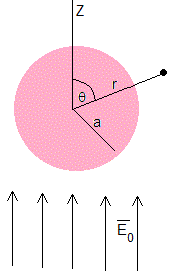
Estudiamos el potencial producido por una esfera dieléctrica de radio a y permitividad relativa ε_r en un campo eléctrico uniforme E₀

El potencial V(r,θ) es

${\displaystyle V(r,\theta )={\displaystyle \sum _{n=0}^{\infty }\left(A_n{r}^n+\frac{B_n}{r^{n+1}}\right)P_n(\cos \theta )}}$

Condiciones de contorno

El potencial en un punto z=rcosθ muy alejado de la esfera de radio a se debe solamente al campo eléctrico uniforme, es V=-E₀rcosθ. Las condiciones de contorno son

${\displaystyle V(\infty ,\theta )=-E_{0}r\cos \theta }$

Potencial eléctrico para r>a

Cuando r es grande los términos B_n/rⁿ⁺¹ tienden a cero, la expresión del potencial será

${\displaystyle -E_{0}r\cos \theta ={\displaystyle \sum _{n=0}^{\infty }{A}_n{r}^n{P}_n(\cos \theta )}}$

Como demostramos en el apartado anterior, todos los coeficientes A_n son ceros excepto A₁=-E₀. La expresión del potencial eléctrico para r>a es

${\displaystyle V_e(r,\theta )={\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{r^{n+1}}{P}_n(\cos \theta )}-E_{0}r\cos \theta }$

Potencial eléctrico para r<a

Cuando r tiende a cero, los términos B_n/rⁿ⁺¹ tienden a infinito, por lo que los coeficientes B_n deberán ser cero. La expresión del potencial será

${\displaystyle V_i(r,\theta )={\displaystyle \sum _{n=0}^{\infty }{A}_n{r}^n{P}_n(\cos \theta )}}$

Superficie de la esfera dieléctrica, r=a

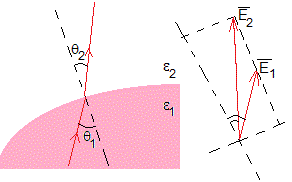
Supongamos dos medios dieléctricos de permitividades ε₁ y ε₂

• El campo eléctrico cambia de módulo y dirección

La componente normal del campo, cumple, ε₁E₁cosθ₁=ε₂E₂cosθ₂. La componente tangencial, no cambia E₁sinθ₁=E₂sinθ₂

${\displaystyle -{\epsilon }_0{\left(\frac{\partial V_e(r,\theta )}{\partial r}\right)}_{r=a}=-\epsilon {\left(\frac{\partial V_i(r,\theta )}{\partial r}\right)}_{r=a}}$

La permitividad relativa del dieléctrico ε_r es el cociente ε/ε₀

${\displaystyle E_0{P}_1(\cos \theta )+{\displaystyle \sum _{n=0}^{\infty }(n+1)\frac{B_n}{a^{n+2}}{P}_n(\cos \theta )}=-{\epsilon }_r\left({\displaystyle \sum _{n=0}^{\infty }n{A}_n{a}^{n-1}{P}_n(\cos \theta )}\right)}$

Esta ecuación ha de ser válida para todo θ. Igualando los coeficientes de los polinomios de Legendre P_n(cosθ), obtenemos el sistema de ecuaciones

${\displaystyle \{\begin{array}{l}\frac{B_0}{a^2}=0\\ E_0+2\frac{B_1}{a^3}=-{\epsilon }_r{A}_1\\ 3\frac{B_2}{a^4}=-{\epsilon }_r·2A_{2}a\\ 4\frac{B_3}{a^5}=-{\epsilon }_r·3A_3{a}^2\\ \mathrm{...}\end{array}}$

• En la superficie del dieléctrico, el potencial es una función continua, V_e(a, θ)=V_i(a, θ)

${\displaystyle {\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{a^{n+1}}{P}_n(\cos \theta )}-E_{0}r\cos \theta ={\displaystyle \sum _{n=0}^{\infty }{A}_n{a}^n{P}_n(\cos \theta )}}$

Igualando los coeficientes de los polinomios de Legendre P_n(cosθ), obtenemos el sistema de ecuaciones

${\displaystyle \{\begin{array}{l}\frac{B_0}{a}=A_0\\ \frac{B_1}{a^2}-E_{0}a=A_{1}a\\ \frac{B_2}{a^3}=A_2{a}^2\\ \frac{B_3}{a^4}=A_3{a}^3\\ \mathrm{....}\end{array}}$

Todos los coeficientes A_n y B_n son nulos excepto

${\displaystyle A_1=\frac{-3}{{\epsilon }_r+2}{E}_0,B_1=\frac{{\epsilon }_r-1}{{\epsilon }_r+2}{E}_0{a}^3}$

Campo eléctrico y potencial

Las expresiones del potencial en el interior y en el exterior del dieléctrico son

${\displaystyle \begin{array}{l}{V}_i(r,\theta )=\frac{-3}{{\epsilon }_r+2}{E}_{0}r\cos \theta \\ V_e(r,\theta )=\frac{{\epsilon }_r-1}{{\epsilon }_r+2}{E}_0{a}^3\frac{\cos \theta }{r^2}-E_{0}r\cos \theta =\left(\frac{{\epsilon }_r-1}{{\epsilon }_r+2}\frac{a^3}{r^3}-1\right)E_{0}r\cos \theta \end{array}}$

Comprobamos que para r=a coinciden

Las expresiones de las componentes del campo eléctrico en el interior y en el exterior del diléctrico son

${\displaystyle \begin{array}{l}r<a\{\begin{array}{l}{E}_r=-\frac{\partial V}{\partial r}=\frac{3}{{\epsilon }_r+2}{E}_0\cos \theta \\ E_{\theta }=-\frac{1}{r}\frac{\partial V}{\partial \theta }=-\frac{3}{{\epsilon }_r+2}{E}_0\sin \theta \end{array}\\ r>a\{\begin{array}{l}{E}_r=-\frac{\partial V}{\partial r}=\left(2\frac{{\epsilon }_r-1}{{\epsilon }_r+2}\frac{a^3}{r^3}+1\right)E_0\cos \theta \\ E_{\theta }=-\frac{1}{r}\frac{\partial V}{\partial \theta }=\left(\frac{{\epsilon }_r-1}{{\epsilon }_r+2}\frac{a^3}{r^3}-1\right)E_0\sin \theta \end{array}\end{array}}$

Comprobamos que para r=a las expresiones de E_θ coinciden y las expresiones de E_r están relacionadas.

Actividades

El programa interactivo muestra las líneas de fuerza y equipotenciales de un campo eléctrico uniforme paralelo al eje X (horizontal) y una esfera dieléctrica de permitividad relativa ε_r.

Se introduce

• el valor del campo eléctrico E₀, en el control titulado Campo eléctrico.
• el valor de la permitividad relativa ε_r, en el control titulado Permitividad relativa.
• el radio a de la esfera se ha fijado en la unidad.

Se pulsa el botón titulado Nuevo

Observamos como se perturba el campo cuando se introduce una esfera dieléctrica en el espacio en el que existe un campo eléctrico uniforme.

Referencias

Lorrain P. Corson D. Campos y ondas electromagnéticas. Selecciones Científicas (1972), págs. 179-182, 185-187