Carga inducida en un conductor esférico
Supongamos un sistema formado por una carga puntual Q en las proximidades de una esfera conductora a potencial cero a una distancia d de su centro. El método de las imágenes nos permite sustituir el conductor por una carga "imagen" q que anulará el potencial sobre la superficie esférica de radio R.
Carga en el interior de la esfera
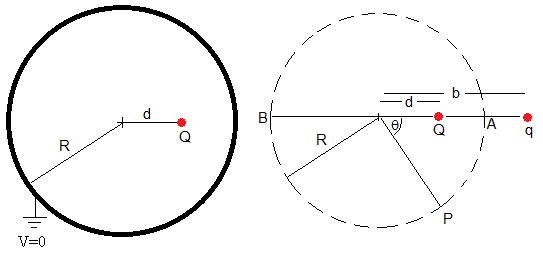
En la parte izquierda de la figura, se muestra la carga Q en el interior de una esfera conductora conectada a tierra
En la parte derecha de la figura, se sustituye la esfera conductora por la carga imagen q situada a una distancia b del centro. Tenemos un sistema de dos cargas puntuales, calculamos q y b sabiendo que el potencial en el punto P es cero
Como esta ecuación se tiene que satisfacer cualesquiera que sea el ángulo θ (el punto P sobre la esfera). El resultado es un sistema de dos ecuaciones con dos incógnitas, q y b
La carga imagen es negativa q=-QR/d situada una distancia b=R2/d del centro. Comprobamos que el potencial en A y en B es cero
Actividades
Se muestra las líneas de campo eléctrico producidas por el sistema de dos cargas, la carga Q y su imanen q
Dentro del conductor el campo eléctrico es nulo. Las líneas de campo eléctrico tienen que terminar perpendiculares a la superficie del conductor
Se introduce
- la distancia d entre la carga puntual Q y el centro de la esfera conductora, en el control titulado Distancia.
- Se han fijado los valores de la carga Q=1 y el radio R=1 de la esfera.
Se pulsa el botón titulado Nuevo
Carga en el exterior de la esfera
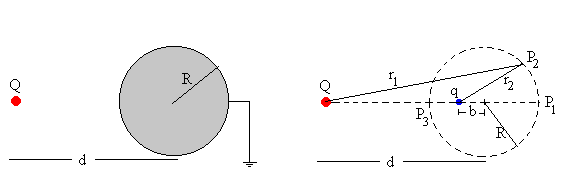
El potencial en el punto P1 de la superficie esférica deberá ser cero
El potencial en el punto P3 diametralmente opuesto deberá ser cero.
Tenemos un sistema de dos ecuaciones con dos incógnitas de las que despejamos q y b.
Demostramos haciendo algunas operaciones que estos valores de q y b hacen que el potencial en cualquier punto P2 de la superficie esférica, sea también cero.
El potencial
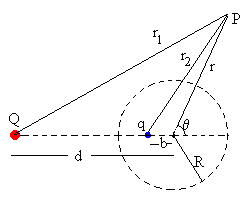
Vamos a calcular el campo en cualquier punto P exterior a la esfera conductora. Primero calculamos el potencial
Se expresa r1 y r2 en coordenadas polares en función de la distancia radial r del centro de la esfera al punto P y del ángulo θ .
De este modo V es una función de r y θ .
La carga inducida en el conductor esférico
Para calcular el vector campo se halla el gradiente del potencial cambiado de signo. El valor de la componente radial del campo es
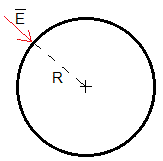
El campo en las proximidades de una superficie conductora es perpendicular a dicha superficie luego, el campo en la superficie esférica conductora es radial. Calculamos Er para r=R y a continuación la densidad superficial de carga inducida en la esfera, teniendo en cuenta que el campo en las proximidades de la superficie de un conductor es Er=σ /ε0
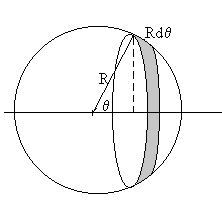
Evidentemente, si integramos esta densidad de carga sobre la superficie de la esfera, obtenemos la carga total inducida q. La integral es inmediata
La carga total inducida sobre la esfera conductora es igual a la carga imagen que sustituye a la esfera.
Este resultado es consecuencia de la ley de Gauss: si dibujamos una superficie cerrada que abarque a la esfera pero que esté muy próxima a ésta, el flujo del campo eléctrico a través de esta superficie debe ser la misma, independientemente, de que la carga esté distribuida sobre la esfera conductora o haya sido sustituida por la carga puntual imagen situada en su interior.
Actividades
Se muestra las líneas de fuerza y equipotenciales de un sistema formado por una carga puntual y una esfera conductora conectada a tierra.
Se introduce
- el valor de la carga puntual Q, en el control titulado Carga.
- la distancia d entre la carga puntual y el centro de la esfera conductora, en el control titulado Distancia.
- el radio R de la esfera se ha fijado en la unidad.
Se pulsa el botón titulado Nuevo
La esfera conductora a potencial cero se sustituye por una carga imagen que aparece como un pequeño círculo de color azul. Observar que la carga imagen es negativa (color azul) si la carga puntual es positiva (color rojo). La carga imagen disminuye al aumentar la separación d y aumenta con la carga puntual Q.
Observar que las líneas de fuerza que llegan al conductor esférico son perpendiculares a su superficie.
Se han trazado las líneas equipotenciales a la izquierda separadas 0.1 unidades. Sin embargo, las líneas equipotenciales de la derecha se han trazado separadas 0.01 unidades arbitrarias.
Activando la casilla de titulada carga inducida desaparece la carga imagen y aparece una distribución de carga sobre la superficie de la esfera conductora en forma de pequeños puntos de color azul que pretenden darnos una idea de la dependencia de la densidad de carga σ con el ángulo θ .
Observamos que la densidad de carga es mayor en la parte de la esfera que está más cerca de la carga puntual positiva y es pequeña, en la parte opuesta, más alejada.
Calculamos la fuerza de atracción entre la carga puntual positiva y la esfera conductora, aplicando la ley de Coulomb a la carga puntual Q y a la carga imagen q, separadas una distancia d-b.
Energía electrostática
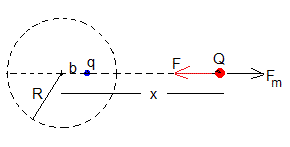
Cuando la carga Q está a una distancia x del centro de la esfera conductora conectada a tierra, la fuerza de atracción F (flecha de color rojo) entre ambas es igual a la fuerza de atracción entre la carga Q y su imagen q situada a una distancia x-b
Calculamos el trabajo de la fuerza Fm=F que hay que hacer para traer la carga Q desde el infinito hasta una distancia d del centro de la esfera conductora.
U es la energía electrostática del sistema formado por la carga Q y su imagen q o bien, por la carga Q y la esfera conductora de radio R conectada a Tierra y separada una distancia d
Tiempo de impacto
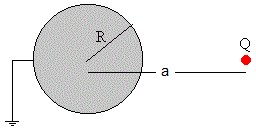
Una partícula de masa m y carga Q se sitúa frente a una esfera conductora de radio R conectada a Tierra. Se suelta la carga Q cuando está a una distancia a del centro de la esfera. Vamos a calcular el tiempo que tarda en chocar con la esfera
La ecuación del movimiento de la partícula cargada es
Teniendo en cuenta
La ecuación del movimiento se escribe
Integramos, teniendo en cuenta que la carga Q parte del reposo v=0, para x=a
Se toma el signo menos de la raíz cuadrada, ya que la partícula cargada se dirige hacia el origen.
Aternativamente, aplicamos el principio de conservación de la energía
Calculamos el tiempo que tarda la partícula cargada que parte de x=a en llegar a la superficie de la esfera x=R
Resolvemos la integral
Para ello, buscamos en la tabla de integrales
I. S. Gradshteyn, I. M. Ryzhik. Table of Integrals, Series, and Products. Eighth Edition. Elsevier.
las integrales 3.152 n° 10 (pág. 282) y 3.153 n° 8 (pág. 283)
Tomando u=R, λ=π/2. El resultado es
E y K son integrales elípticas completas
Cuando el radio R de la esfera es grande comparado con a, la superficie esférica se aproxima a una plana.
En la página titulada Carga inducida en un conductor plano en el apartado 'Movimiento de la carga hacia el plano conductor', calculamos el tiempo T0 que tarda en chocar una partícula de masa m y carga Q con la placa plana conductora conectada a tierra
Teniendo en cuenta que d=a-R. El cociente entre T/T0 es
Ejemplo, R=10,20,30..., a=R=1. La distancia a la placa es d=a-R=1
for R=10:10:50 %radio
a=R+1; %distancia a la placa d=a-R=1
[K,E]=ellipke(1-R^2/a^2);
cociente=a*sqrt(2*(a+R)/(R*(a-R)^2))*(E-K*R^2/a^2)/pi;
disp([R,cociente])
end
10.0000 1.0009 20.0000 1.0002 30.0000 1.0001 40.0000 1.0001 50.0000 1.0000
Movimiento de una partícula cargada alrededor de una esfera conductora
En la página titulada Ecuación de la trayectoria, estudiamos el movimiento de un cuerpo celeste en la dirección radial, representando la energía potencial efectiva en función de r
Determinamos las posibles trayectorias de un cuerpo celeste para un valor dado de su energía total.
En este apartado vamos a estudiar las posibles trayectorias de una carga puntual -q que se mueve alrededor de un esfera conductora cargada con carga Q. Veremos que la carga inducida por la carga puntual -q en la esfera conductora complica considerablemente el problema.
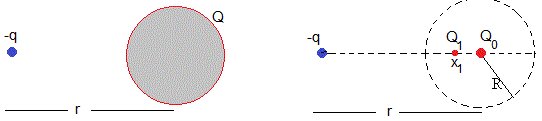
Consideremos una esfera conductora con carga Q y radio R, y una carga puntual -q distante r de su centro.
Debido a la presencia de la carga -q la carga de la esfera se redistribuye y es equivalente a dos cargas Q0=Q-Q1 situada en el centro y Q1=Rq/r situada en x1=R2/r.
Cuanto más pequeña es la distancia r mayores son los efectos de la polarización de la carga -q, Q1 es mayor
Es una fuerza conservativa y la energía potencial es
Se ha establecido el nivel cero de energía potencial en el infinito
La energía potencial efectiva es
Establecemos las siguientes escalas
La energía potencial efectiva se expresa en términos de magnitudes adimensionaes
Volvemos a la notación anterior, para retener el significado de los distintos términos
Asignamos a Q=1. Representamos Uef(r) para L2=2.83.
Q=1;
L2=2.83;
f=@(x) (L2+1)./(2*x.^2)-Q./x-1./(2*(x.^2-1));
fplot(f,[1.5,3.3])
grid on
xlabel('r')
ylabel ('U_{ef}')
title('Energía potencial efectiva')
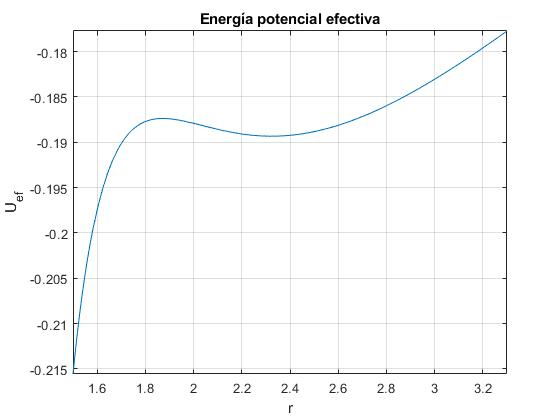
La función Uef(r) tiene un máximo y un mínimo local. Derivamos con respecto a r e igualamos a cero.
>> raices=roots([Q,-L2,-2*Q,2*(L2+1),Q,-(L2+1)])
raices =
2.3238
1.8721
-1.3363
-0.8266
0.7970
Para r=2.32 tenemos un mínimo (una órbita circular estable) y para r=1.87 un máximo (una órbita circular inestable), como puede comprobarse con la derivada segunda. En el máximo es negativa y en el mínimo es positiva
ff=@(x) 3*(L2+1)/x^4-2*Q/x^3-(3*x^2+1)/(x^2-1)^3; >> ff(raices(1)) ans = 0.0327 >> ff(raices(2)) ans = -0.1022
Para L2=2.7, no hay máximo ni mínimo.
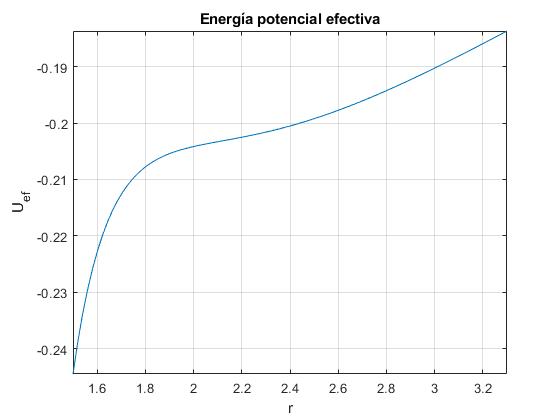
Lo que implica que habrá un valor de L2 comprendido entre 2.83 y 2.7 crítico con un punto de inflexión donde se juntan el máximo y mínimo locales.
Se cumplirá a la vez que la derivada primera es nula y la derivada segunda también. Resolvemos el sistema de dos ecuaciones
Multiplicamos la primera por 3 y la segunda por r y sumamos
Llamamos
Conocido z se calcula rc, raíz positiva de la ecuación de segundo grado
Con Q=1, rc=2.0704, tomamos una de las ecuaciones para calcular L2
El resultado es L2=2.7715
>> z=nthroot(2,3) z = 1.2599 >> (1+sqrt(z^2+1))/z ans = 2.0704 >> r+r^4/(r^2-1)^2-1 ans = 2.7715
Representamos Uef(r) para L2=2.83, 2.7715 y 2.7
Q=1;
hold on
for L2=[2.83, 2.7715,2.7]
f=@(x) (L2+1)./(2*x.^2)-Q./x-1./(2*(x.^2-1));
fplot(f,[1.6,3],'displayName',num2str(L2))
end
hold off
grid on
xlabel('r')
legend('-DynamicLegend','location','southeast')
ylabel ('U_{ef}')
title('Energía potencial efectiva')
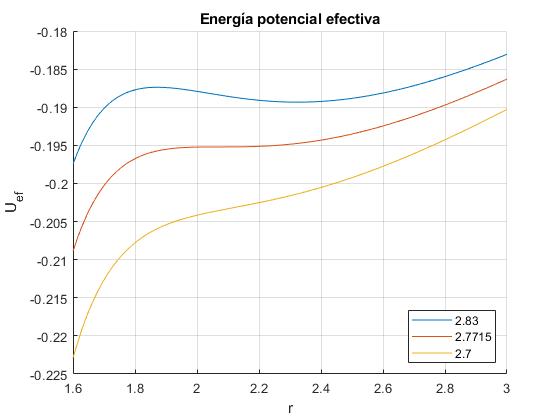
Por debajo del valor crítico adimensional, L2=2.7715 no hay órbitas estables ni inestables. Luego, habrá que convertir L en un valor físico concreto conocidas la carga, q y la masa m de la carga puntal, el radio R y la carga Q de la esfera cargada
Referencias
Lorrain P. Corson D. Campos y ondas electromagnéticas. Selecciones Científicas (1972), págs. 156-158
Shubho Banerjee, Bradford Taylor. On the stability of electrostatic orbits. Am. J. Phys. 77 (5) May 2009, pp. 396-400
LI Li,ZHANG Yin. An analytic solution and asymptotic behavior for traction time of point charge to grounded conducting sphere. College Physics 20 January 2018, Volume 37, Issue 1

