Un hilo rectilíneo cargado paralelo a un conductor plano conectado a tierra

En la página titulada Principio de superposición de campos, calculamos el campo eléctrico y el potencial producido por dos hilos rectilíneos cargados con +λ y -λ C/m, paralelos y distantes 2a. Representamos las líneas de fuerza (en color rojo) y equipotenciales (en color azul)

a=1; % 2a es la distancia entre los dos hilos
hold on
for k=[1:4, -(1:4)]
   R=sqrt(a^2+k^2);
   y1=k;
   fplot(@(t) R*cos(t), @(t) y1+R*sin(t),[0,2*pi],'r')
end
for k=[0.3:0.1:0.6, 1./(0.3:0.1:0.6)]
   R=2*a*sqrt(k)/(1-k);
   x1=(1+k)*a/(1-k);
   fplot(@(t) x1+R*cos(t), @(t) R*sin(t),[0,2*pi],'b')
end
plot(-a,0,'ro','markersize',4,'markerfacecolor','r') %hilos
plot(a,0,'bo','markersize',4,'markerfacecolor','b')
hold off
axis equal
% grid on
xlabel('x')
ylabel('y');
title('Líneas de fuerza y equipotenciales')

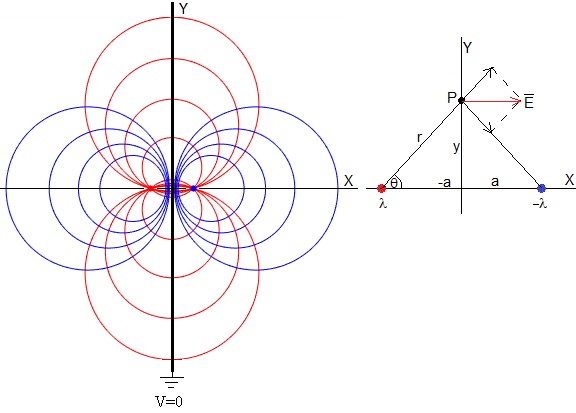
Un hilo rectilíneo cargado paralelo a un conductor plano conectado a tierra es equivalente a dos hilos conductores, el hilo imagen cargado con -λ C/m, situado detrás del plano conductor x=0, a la misma distancia a

El campo eléctrico en los puntos del plano x=0, es perpendicular al placa conductora

El campo eléctrico en las proximidades de un conductor, tiene por módulo E=σ/ε₀. Donde σ es la densidad de de carga. Como el sentido del campo eléctrico es hacia el conductor, la densidad de carga σ es negativa σ=-E·ε₀

${\displaystyle \sigma =-{\epsilon }_{0}E=-{\epsilon }_0\left(2\frac{\lambda }{2\pi {\epsilon }_{0}r}\cos \theta \right)=-\frac{\lambda }{\pi }\frac{a}{a^2+y^2}}$

a=1;
f=@(x) -a./(a^2+x.^2);
fplot(f,[-5,5])
grid on
xlabel('y')
ylabel('\sigma')
title('Densidad de carga')

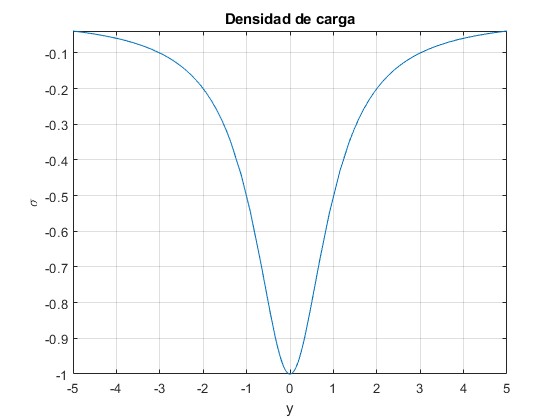
La carga dq inducida en la franja de longitud unidad y anchura dy es dq=σ(1·dy). La carga total inducida en el plano conductor (por unidad de longitud) se calcula integrando respecto de y entre -∞ e +∞

${\displaystyle Q={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\left(-\frac{\lambda }{\pi }\frac{a}{a^2+y^2}\right)(1·dy})=-\frac{\lambda a}{\pi }\frac{1}{a}{\arctan \left(\frac{y}{a}\right)|}_{-\infty }^{\infty }=-\frac{\lambda }{\pi }\left(\frac{\pi }{2}-\left(-\frac{\pi }{2}\right)\right)=-\lambda }$

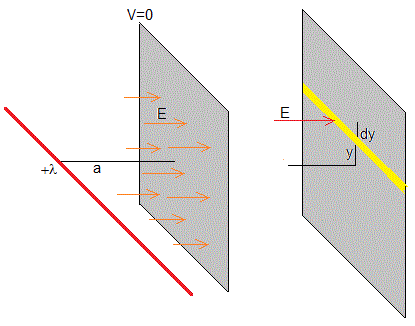
que es la carga imagen por unidad de longitud

Un hilo rectilíneo cargado entre dos planos conductores perpendiculares

Consideremos un hilo rectilíneo indefinido, cuya carga es λ C/m, paralelo al eje Z, y dos placas conductoras planas e indefinidas conectadas a tierra, que se cruzan a lo largo del eje Z formando un ángulo de 90°. En la figura, se representa el corte en el plano z=0, es decir, el plano XY

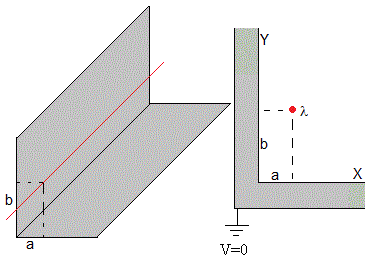
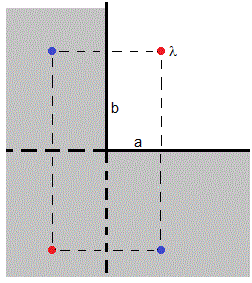
Situamos un hilo rectilíneo cargado +λ en el punto de coordenadas polares (a, b).

• El hilo imagen de +λ (a, b) producida por el plano horizontal y=0 es -λ en color azul, situado en (a, -b)

• El hilo imagen de +λ, (a, b) producida por el plano vertical x=0 es -λ en color azul, situado en (-a, b)

• El hilo imagen de -λ (-a, b) producida por el plano y=0 es +λ en color rojo, situada en (-a, -b). Del mismo modo, el hilo imagen de -λ (a, -b) producida por el plano x=0 es +λ en color rojo, situada en (-a, -b)

Como vemos en la figura, se han representado el hilo cargado +λ y sus imágenes.

Campo eléctrico

El campo producido por un hilo rectilíneo cargado con λ C/m a una distancia r del hilo es

${\displaystyle E=\frac{\lambda }{2\pi {\epsilon }_{0}r}}$

tiene dirección radial perpendicular a hilo cargado

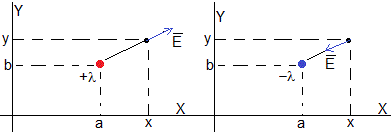
El campo eléctrico producido por las cuatro líneas de carga en los puntos (x,y) es

${\displaystyle \begin{array}{l}\overrightarrow{E_1}=\frac{\lambda }{2\pi {\epsilon }_0\sqrt{{\left(x-a\right)}^2+{\left(y-b\right)}^2}}\frac{\left(x-a\right)\widehat{i}+\left(y-b\right)\widehat{j}}{\sqrt{{\left(x-a\right)}^2+{\left(y-b\right)}^2}}=\frac{\lambda \left(\left(x-a\right)\widehat{i}+\left(y-b\right)\widehat{j}\right)}{2\pi {\epsilon }_0\left({\left(x-a\right)}^2+{\left(y-b\right)}^2\right)}\\ \overrightarrow{E_2}=\frac{-\lambda \left(\left(x-a\right)\widehat{i}+\left(y+b\right)\widehat{j}\right)}{2\pi {\epsilon }_0\left({\left(x-a\right)}^2+{\left(y+b\right)}^2\right)}\\ \overrightarrow{E_3}=\frac{\lambda \left(\left(x+a\right)\widehat{i}+\left(y+b\right)\widehat{j}\right)}{2\pi {\epsilon }_0\left({\left(x+a\right)}^2+{\left(y+b\right)}^2\right)}\\ \overrightarrow{E_4}=\frac{-\lambda \left(\left(x+a\right)\widehat{i}+\left(y-b\right)\widehat{j}\right)}{2\pi {\epsilon }_0\left({\left(x+a\right)}^2+{\left(y-b\right)}^2\right)}\\ \overrightarrow{E}=\frac{\lambda }{2\pi {\epsilon }_0}\left(\begin{array}{l}\left\{\frac{x-a}{{\left(x-a\right)}^2+{\left(y-b\right)}^2}-\frac{x-a}{{\left(x-a\right)}^2+{\left(y+b\right)}^2}+\frac{x+a}{{\left(x+a\right)}^2+{\left(y+b\right)}^2}-\frac{x+a}{{\left(x+a\right)}^2+{\left(y-b\right)}^2}\right\}\widehat{i}+\\ \left\{\frac{y-b}{{\left(x-a\right)}^2+{\left(y-b\right)}^2}-\frac{y+b}{{\left(x-a\right)}^2+{\left(y+b\right)}^2}+\frac{y+b}{{\left(x+a\right)}^2+{\left(y+b\right)}^2}-\frac{y-b}{{\left(x+a\right)}^2+{\left(y-b\right)}^2}\right\}\widehat{j}\end{array}\right)\\ \end{array}}$

Comprobamos que el campo eléctrico en los puntos (x,0) del plano y=0 es perpendicular a este plano, tiene la dirección del eje Y

${\displaystyle \overrightarrow{E}=\frac{\lambda b}{\pi {\epsilon }_0}\left\{-\frac{1}{{\left(x-a\right)}^2+b^2}+\frac{1}{{\left(x+a\right)}^2+b^2}\right\}\widehat{j}}$

Comprobamos que el campo eléctrico en los puntos (0, y) del plano x=0 es perpendicular a este plano, tiene la dirección del eje X

${\displaystyle \overrightarrow{E}=\frac{\lambda a}{\pi {\epsilon }_0}\left\{\frac{-1}{a^2+{\left(y-b\right)}^2}+\frac{1}{a^2+{\left(y+b\right)}^2}\right\}\widehat{i}}$

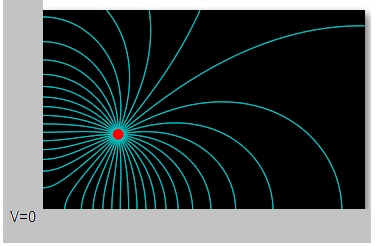
Potencial

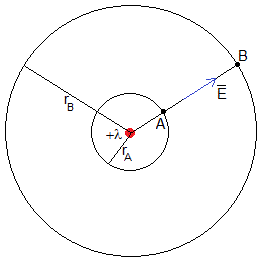
La diferencia de potencial entre dos puntos A y B situados a distancias r_A y r_B del hilo rectilíneo cargado con λ C/m es

${\displaystyle V_A-V_B={\displaystyle \underset{r_A}{\overset{r_B}{\int }}\frac{\lambda }{2\pi {\epsilon }_{0}r}dr}=\frac{\lambda }{2\pi {\epsilon }_0}\ln \frac{r_B}{r_A}}$

Calculamos el potencial en el punto A (x, y), situando el punto B en el origen (0,0) y tomando el potencial de B cero, V(0)=0

El potencial en el punto (x, y) producido por el hilo rectilíneo cargado +λ situado en el punto (a, b) es

${\displaystyle V_1=\frac{\lambda }{2\pi {\epsilon }_0}\ln \frac{\sqrt{a^2+b^2}}{\sqrt{{\left(x-a\right)}^2+{\left(y-b\right)}^2}}=\frac{\lambda }{4\pi {\epsilon }_0}\ln \frac{a^2+b^2}{{\left(x-a\right)}^2+{\left(y-b\right)}^2}}$

De forma similar

${\displaystyle \begin{array}{l}{V}_2=\frac{-\lambda }{4\pi {\epsilon }_0}\ln \frac{a^2+b^2}{{\left(x-a\right)}^2+{\left(y+b\right)}^2}\\ V_3=\frac{\lambda }{4\pi {\epsilon }_0}\ln \frac{a^2+b^2}{{\left(x+a\right)}^2+{\left(y+b\right)}^2}\\ V_4=\frac{-\lambda }{4\pi {\epsilon }_0}\ln \frac{a^2+b^2}{{\left(x+a\right)}^2+{\left(y-b\right)}^2}\\ V=\frac{\lambda }{4\pi {\epsilon }_0}\ln \frac{\left({\left(x+a\right)}^2+{\left(y-b\right)}^2\right)\left({\left(x-a\right)}^2+{\left(y+b\right)}^2\right)}{\left({\left(x-a\right)}^2+{\left(y-b\right)}^2\right)\left({\left(x+a\right)}^2+{\left(y+b\right)}^2\right)}\end{array}}$

Comprobamos que que el potencial de los puntos (x,0) del plano y=0, es nulo

${\displaystyle V\left(x\mathrm{,0}\right)=\frac{\lambda }{4\pi {\epsilon }_0}\ln \frac{\left({\left(x+a\right)}^2+b^2\right)\left({\left(x-a\right)}^2+b^2\right)}{\left({\left(x-a\right)}^2+b^2\right)\left({\left(x+a\right)}^2+b^2\right)}=0}$

Comprobamos que que el potencial de los puntos (0, y) del plano x=0, es nulo

${\displaystyle V\left(\mathrm{0,}y\right)=\frac{\lambda }{4\pi {\epsilon }_0}\ln \frac{\left(a^2+{\left(y-b\right)}^2\right)\left(a^2+{\left(y+b\right)}^2\right)}{\left(a^2+{\left(y-b\right)}^2\right)\left(a^2+{\left(y+b\right)}^2\right)}=0}$

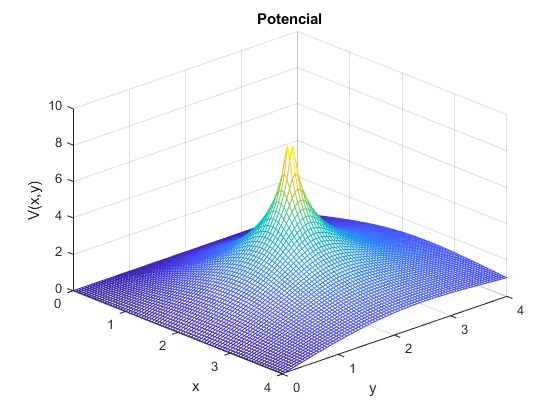
Representamos la función V(x,y) para a=2 y b=2

a=2;
b=2;
[x,y] = meshgrid(0:0.05:4, 0:0.05:4);
V=@(x,y) log(((x+a).^2+(y-b).^2).*((x-a).^2+(y+b).^2)./
(((x-a).^2+(y-b).^2).*((x+a).^2+(y+b).^2)));
z=V(x,y);
mesh(x,y,z)
xlabel('x')
ylabel('y')
zlabel('V(x,y)')
title('Potencial')
view(47,32)

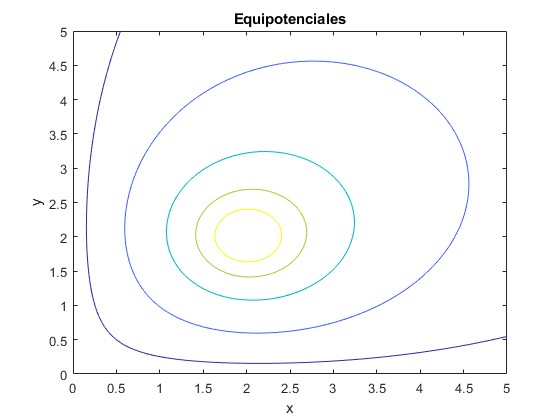
Representamos las líneas equipotenciales con fcontour de MATLAB

a=2;
b=2;
V=@(x,y) log(((x+a).^2+(y-b).^2).*((x-a).^2+(y+b).^2)./
(((x-a).^2+(y-b).^2).*((x+a).^2+(y+b).^2)));
fcontour(V,[0,5,0,5],'LevelList',[0.25, 1:4])
xlabel('x')
ylabel('y')
title('Equipotenciales')

Fuerza sobre el hilo rectilíneo cargado

Calculamos la fuerza que ejercen las cargas inducidas en los dos planos conductores conectados a tierra sobre el hilo rectilíneo cargado con +λ C/m

El campo eléctrico producido por las tres cargas imagen en el punto (a, b) es

${\displaystyle \begin{array}{l}\overrightarrow{E_2}=\frac{-2\lambda b\widehat{j}}{2\pi {\epsilon }_{0}4b^2}=-\frac{\lambda }{4\pi {\epsilon }_{0}b}\widehat{j}\\ \overrightarrow{E_3}=\frac{2\lambda \left(a\widehat{i}+b\widehat{j}\right)}{2\pi {\epsilon }_0\left(4a^2+4b^2\right)}=\frac{\lambda \left(a\widehat{i}+b\widehat{j}\right)}{4\pi {\epsilon }_0\left(a^2+b^2\right)}\\ \overrightarrow{E_4}=\frac{-2\lambda a\widehat{i}}{2\pi {\epsilon }_0\left(4a^2\right)}=-\frac{\lambda }{4\pi {\epsilon }_{0}a}\widehat{i}\\ \overrightarrow{E}=\overrightarrow{E_2}+\overrightarrow{E_3}+\overrightarrow{E_4}=\frac{\lambda }{4\pi {\epsilon }_{0}b}\left\{\frac{a\widehat{i}+b\widehat{j}}{a^2+b^2}-\frac{1}{a}\widehat{i}-\frac{1}{b}\widehat{j}\right\}\end{array}}$

La fuerza sobre la longitud l de hilo recilíneo cargado con +λ C/m es

${\displaystyle \overrightarrow{F}=\lambda l\overrightarrow{E}=\frac{{\lambda }^{2}l}{4\pi {\epsilon }_{0}b}\left\{\frac{a\widehat{i}+b\widehat{j}}{a^2+b^2}-\frac{1}{a}\widehat{i}-\frac{1}{b}\widehat{j}\right\}}$

Actividades

Se muestran las líneas de fuerza del sistema formado por el hilo rectilíneo cargado +λ situado en la posición (a, b) y sus hilos imagen

Se introduce

• La abscisa a en el control titulado Abscisa a
• La ordenada b en el control titulado Ordenada b
• Se ha fijado $\frac{\lambda }{2\pi {\epsilon }_0}=1$

Se pulsa el botón titualado Nuevo

Referencias

D. K. Ghosh. Lecture 19: Electromagnetic Theory. Example: Line charge near a conducting cylinder. Physics Department, I.I.T., Bombay

Pan Pearl River Delta Physics Olympiad 2018, Q4