Una serie de Taylor es una aproximación de una función mediante un polinomio

El desarrollo de Taylor de una función y(x) alrededor de un punto x₀ es

${\displaystyle y(x)=y(x_0)+{\frac{dy}{dx}|}_{x_0}(x-x_0)+\frac{1}{2}{\frac{d^{2}y}{d{x}^2}|}_{x_0}{\left(x-x_0\right)}^2+\mathrm{...}\frac{1}{n!}{\frac{d^{n}y}{d{x}^n}|}_{x_0}{\left(x-x_0\right)}^n+\mathrm{...}}$

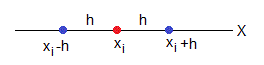
El desarrollo de Taylor hasta n=2 alrededor del punto x_i es

${\displaystyle \begin{array}{l}y(x_{i+1})=y(x_i+h)=y(x_i)+h{\frac{dy}{dx}|}_{x_i}+\frac{h^2}{2}{\frac{d^{2}y}{d{x}^2}|}_{x_i}+\mathrm{...}\\ y(x_{i-1})=y(x_i-h)=y(x_i)-h{\frac{dy}{dx}|}_{x_i}+\frac{h^2}{2}{\frac{d^{2}y}{d{x}^2}|}_{x_i}+\mathrm{...}\end{array}}$

Sumamos ambas ecuaciones y despejamos a derivada segunda de la función en x_i

${\displaystyle {\frac{d^{2}y}{d{x}^2}|}_{x_i}\approx \frac{y(x_{i+1})+y(x_{i-1})-2y(x_i)}{h^2}}$

El potencial V(x,y) es una función de dos variables, solución de la ecuación de Laplace

${\displaystyle \frac{{\partial }^{2}V}{\partial x^2}+\frac{{\partial }^{2}V}{\partial y^2}=0}$

Sustituimos las derivadas parciales por sus expresiones aproximadas en el punto (x_i, y_i)

${\displaystyle \begin{array}{l}\frac{V(x_{i+1},y_j)+V(x_{i-1},y_i)-2V(x_i,y_j)}{h^2}+\frac{V(x_i,y_{j+1})+V(x_i,y_{j-1})-2V(x_i,y_j)}{h^2}\approx 0\\ 4V(x_i,y_j)=V(x_{i+1},y_j)+V(x_{i-1},y_j)+V(x_i,y_{j+1})+V(x_i,y_{j-1})\end{array}}$

Consideremos un recinto rectangular de dimensiones a y b. Dividimos el eje X en m+1 intervalos, a=(m+1)h y el eje Y en n+1 intervalos, b=(n+1)h

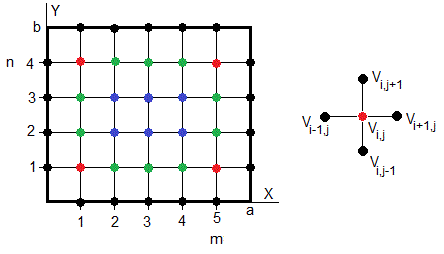
Las coordenadas de un punto interior cualquiera de la malla son, x_i=i·h, y_j=j·h (i=1,2...m, j=1,2,...n)

Conocidos los potenciales en el borde, V(0,y_j), V(x_i,0), V(a,y_j), V(x_i,b) (en color negro), calcularemos los potenciales V_i,j en los puntos del interior, en color rojo, verde y azul, (x_i,y_j), (i=1,2...m, j=1,2,...n).

Sistema de ecuaciones lineales

El potencial V_i,j del punto (x_i,y_j) se calcula a partir de los potenciales de los cuatro más próximos, tal como se muestra en la figura de la derecha

${\displaystyle 4V_{i,j}=V_{i+\mathrm{1,}j}+V_{i-\mathrm{1,}j}+V_{i,j+1}+V_{i,j-1}}$

Consideremos el ejemplo de la figura, m=5 y n=4. Pondremos a la izquierda del signo de la igualdad las incógnitas y a la derecha los datos. Tendremos un sistema lineal de m·n=5·4=20 ecuaciones con 20 incógnitas. Distinguiremos tres regiones:

1. Esquinas, puntos de color rojo

4V₁₁-V₂₁-V₁₂=V₀₁+V₁₀
-V₄₁+4V₅₁-V₅₂=V₅₀+V₆₁
-V₁₃+4V₁₄-V₂₄=V₀₄+V₁₅
-V₅₃-V₄₄+4V₅₄=V₅₅+V₆₄


2. Puntos de color verde, cerca del borde

• Parte inferior

-V₁₁+4V₂₁-V₃₁-V₂₂=V₂₀
-V₂₁+4V₃₁-V₄₁-V₃₂=V₃₀
-V₃₁+4V₄₁-V₅₁-V₄₂=V₄₀


• Parte superior

-V₁₄+4V₂₄-V₃₄-V₂₃=V₂₅
-V₂₄+4V₃₄-V₄₄-V₃₃=V₃₅
-V₃₄+4V₄₄-V₅₄-V₄₃=V₄₅


• Parte izquierda

-V₁₁+4V₁₂-V₁₃-V₂₂=V₀₂
-V₁₂+4V₁₃-V₂₃-V₁₄=V₀₃


• Parte derecha

-V₅₁+4V₅₂-V₅₃-V₄₂=V₆₂
-V₅₂+4V₅₃-V₅₄-V₄₃=V₆₃


3. Puntos interiores, de color azul

4V₂₂-V₁₂-V₃₂-V₂₁-V₂₃=0
4V₃₂-V₂₂-V₄₂-V₃₁-V₃₃=0
4V₄₂-V₃₂-V₅₂-V₄₁-V₄₃=0
4V₂₃-V₁₃-V₃₃-V₂₄-V₂₂=0
4V₃₃-V₂₃-V₄₃-V₃₄-V₃₂=0
4V₄₃-V₃₃-V₅₃-V₄₄-V₄₂=0

Escribimos el sistema de ecuaciones de forma matricial, A·X=B

${\displaystyle \left(\begin{array}{cccccccccccccccccccc}4& -1& 0& 0& 0& -1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ -1& 4& -1& 0& 0& 0& -1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& -1& 4& -1& 0& 0& 0& -1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& -1& 4& -1& 0& 0& 0& -1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& -1& 4& 0& 0& 0& 0& -1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ -1& 0& 0& 0& 0& 4& -1& 0& 0& 0& -1& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& -1& 0& 0& 0& -1& 4& -1& 0& 0& 0& -1& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& -1& 0& 0& 0& -1& 4& -1& 0& 0& 0& -1& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& -1& 0& 0& 0& -1& 4& -1& 0& 0& 0& -1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& -1& 0& 0& 0& -1& 4& 0& 0& 0& 0& -1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& -1& 0& 0& 0& 0& 4& -1& 0& 0& 0& -1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& -1& 0& 0& 0& -1& 4& -1& 0& 0& 0& -1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& -1& 0& 0& 0& -1& 4& -1& 0& 0& 0& -1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& -1& 0& 0& 0& -1& 4& -1& 0& 0& 0& -1& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& -1& 0& 0& 0& -1& 4& 0& 0& 0& 0& -1\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& -1& 0& 0& 0& 0& 4& -1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& -1& 0& 0& 0& -1& 4& -1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& -1& 0& 0& 0& -1& 4& -1& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& -1& 0& 0& 0& -1& 4& -1\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& -1& 0& 0& 0& -1& 4\end{array}\right)\left(\begin{array}{c}{V}_{11}\\ V_{21}\\ V_{31}\\ V_{41}\\ V_{51}\\ V_{12}\\ V_{22}\\ V_{32}\\ V_{42}\\ V_{52}\\ V_{13}\\ V_{23}\\ V_{33}\\ V_{43}\\ V_{53}\\ V_{14}\\ V_{24}\\ V_{34}\\ V_{44}\\ V_{54}\end{array}\right)=\left(\begin{array}{c}{V}_{10}+V_{01}\\ V_{20}\\ V_{30}\\ V_{40}\\ V_{50}+V_{61}\\ V_{02}\\ 0\\ 0\\ 0\\ V_{62}\\ V_{03}\\ 0\\ 0\\ 0\\ V_{63}\\ V_{04}+V_{15}\\ V_{25}\\ V_{35}\\ V_{45}\\ V_{55}+V_{64}\end{array}\right)}$

Matriz de los coeficientes

Dividimos la matriz A de los coeficientes en submatrices que se repiten, tal como se muestra en la figura

La submatriz D cuadrada de dimensión m=5, se repite a lo largo de la diagonal de la matriz A, se repite también la matriz diagonal E y la matriz nula O, todas de la misma dimensión. El diagrama de bloques se muestra en la figura

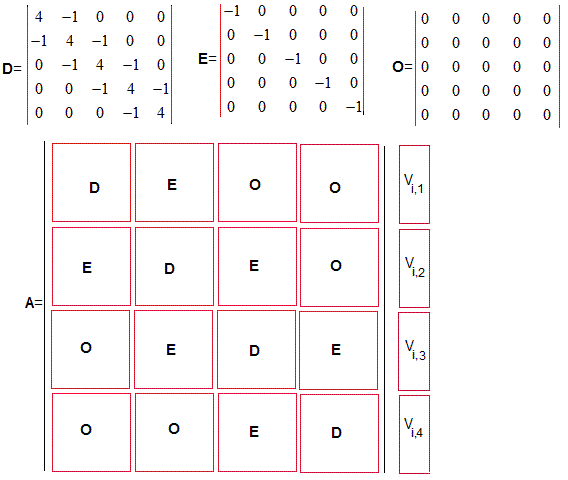
MATLAB facilita el trabajo con matrices: crear matrices, acceder a sus elementos, etc. El código para crear la matriz A de los coeficientes de dimensión m·n a partir de las submatrices D y E de dimensión m es

A=zeros(n*m);
D=diag(4*ones(1,m))+diag(-1*ones(1,m-1),1)+diag(-1*ones(1,m-1),-1);
E=diag(-1*ones(1,m));
for i=0:n-1
    A(1+i*m:(i+1)*m,1+i*m:(i+1)*m)=D;
end
for i=1:n-1
    A(1+i*m:(i+1)*m,1+(i-1)*m:m*i)=E;
    A(1+(i-1)*m:i*m,1+i*m:(i+1)*m)=E;
end

Este código vale para cualquier problema, basta especificar el número de intervalos m y n

Vector de los términos independientes

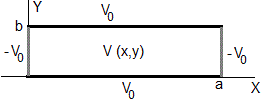
Más trabajo requiere especificar las condiciones de contorno, el vector B de los términos independientes. Supongamos que las condiciones de contorno son

${\displaystyle \{\begin{array}{l}{V}_{\mathrm{0,}j}=-V_{0}j=\mathrm{1,2...}n\\ V_{m+\mathrm{1,}j}=-V_{0}j=\mathrm{1,2...}n\\ V_{i\mathrm{,0}}=V_{0}i=\mathrm{1,2...}m\\ V_{i,n+1}=V_{0}i=\mathrm{1,2...}m\end{array}}$

Primero crearemos una función que traslade la posición de un punto interior (i,j) en su posición k en el vector columna B. Por ejemplo, la posición de la incógnita V_2,3 es k=12

...
f=@(i,j) i+(j-1)*m;
...

Los términos independientes distintos de cero, son producidos por los cuatro puntos rojos de las esquinas y los puntos verdes próximos al borde. Los puntos interiores, (de color azul) dan lugar a un valor nulo

El código para crear el vector B es el siguiente

...
    %condiciones de contorno
VS=ones(1,m); %abajo
VN=ones(1,m); %arriba
VE=-ones(1,n); %derecha
VO=-ones(1,n); %izquierda
f=@(i,j) i+(j-1)*m;
%Vector términos independientes
B=zeros(n*m,1);
%puntos rojos
B(f(1,1))=VO(1)+VS(1);
B(f(m,1))=VS(m)+VE(1);
B(f(1,n))=VN(1)+VO(n);
B(f(m,n))=VN(m)+VE(n);
%puntos verdes
for k=2:m-1
    B(f(k,1))=VS(k);
    B(f(k,n))=VN(k);
end
for k=2:n-1
    B(f(1,k))=VO(k);
    B(f(m,k))=VE(k);
end

Vector de las incógnitas

Una vez que hemos definido el vector A de los coeficientes y el vector B de los términos independientes, despejamos el vector X de las incógnitas, A·X=B, utilizando el operador división por la izquierda '\'

...
X=A\B;
R=zeros(n,m);
for j=1:n
    for i=1:m
        k=f(i,j);
        R(n+1-j,i)=X(k);
     end
end
...

Los valores del potencial V_i,j en los puntos interiores del recinto rectangular son

R =
    0.0390    0.4286    0.5325    0.4286    0.0390
   -0.2727    0.1429    0.2727    0.1429   -0.2727
   -0.2727    0.1429    0.2727    0.1429   -0.2727
    0.0390    0.4286    0.5325    0.4286    0.0390

Como cabría esperar, hay simetría en los valores del potencial

Solución analítica

En la página previa titulada La ecuación de Laplace, coordenadas rectangulares, estudiamos el caso general. El potencial V(x,y) es la suma de cuatro contribuciones, tal como se muestra en la figura

${\displaystyle \begin{array}{l}{V}_1(x,y)=\frac{2}{b}{\displaystyle \sum _{n=1}^{\infty }\left({\displaystyle \underset{0}{\overset{b}{\int }}V(\mathrm{0,}y)\sin \left(\frac{n\pi }{b}y\right)dy}\left\{\frac{\sinh \left(\frac{n\pi }{b}(a-x)\right)}{\sinh \left(\frac{n\pi }{b}a\right)}\right\}\sin \left(\frac{n\pi }{b}y\right)\right)}=-\frac{4V_0}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\left(\frac{1}{n}\left\{\frac{\sinh \left(\frac{n\pi }{b}(a-x)\right)}{\sinh \left(\frac{n\pi }{b}a\right)}\right\}\sin \left(\frac{n\pi }{b}y\right)\right)}\\ V_2(x,y)=\frac{2}{b}{\displaystyle \sum _{n=1}^{\infty }\left({\displaystyle \underset{0}{\overset{b}{\int }}V(a,y)\sin \left(\frac{n\pi }{b}y\right)dy}\left\{\frac{\sinh \left(\frac{n\pi }{b}x\right)}{\sinh \left(\frac{n\pi }{b}a\right)}\right\}\sin \left(\frac{n\pi }{b}y\right)\right)}=-\frac{4V_0}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\left(\frac{1}{n}\left\{\frac{\sinh \left(\frac{n\pi }{b}x\right)}{\sinh \left(\frac{n\pi }{b}a\right)}\right\}\sin \left(\frac{n\pi }{b}y\right)\right)}\\ V_3(x,y)=\frac{2}{a}{\displaystyle \sum _{n=1}^{\infty }\left({\displaystyle \underset{0}{\overset{a}{\int }}V(x\mathrm{,0})\sin \left(\frac{n\pi }{a}x\right)dx}\left\{\frac{\sinh \left(\frac{n\pi }{a}(b-y)\right)}{\sinh \left(\frac{n\pi }{a}b\right)}\right\}\sin \left(\frac{n\pi }{a}x\right)\right)}=\frac{4V_0}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\left(\frac{1}{n}\left\{\frac{\sinh \left(\frac{n\pi }{a}(b-y)\right)}{\sinh \left(\frac{n\pi }{a}b\right)}\right\}\sin \left(\frac{n\pi }{a}x\right)\right)}\\ V_4(x,y)=\frac{2}{a}{\displaystyle \sum _{n=1}^{\infty }\left({\displaystyle \underset{0}{\overset{a}{\int }}V(x,b)\sin \left(\frac{n\pi }{a}x\right)dx}\left\{\frac{\sinh \left(\frac{n\pi }{a}y\right)}{\sinh \left(\frac{n\pi }{a}b\right)}\right\}\sin \left(\frac{n\pi }{a}x\right)\right)}=\frac{4V_0}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\left(\frac{1}{n}\left\{\frac{\sinh \left(\frac{n\pi }{a}y\right)}{\sinh \left(\frac{n\pi }{a}b\right)}\right\}\sin \left(\frac{n\pi }{a}x\right)\right)}\end{array}}$

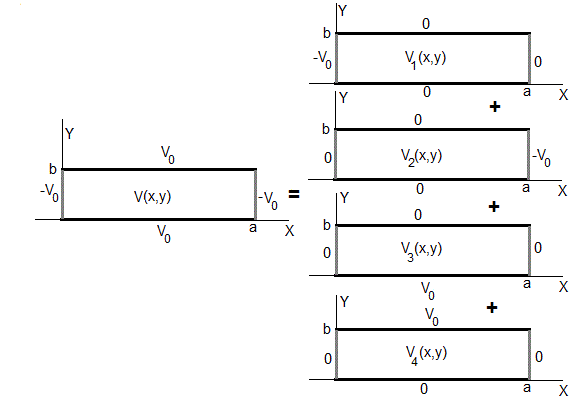
El resultado de la suma de las cuatro contribuciones es

${\displaystyle V(x,y)=\frac{4V_0}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{1}{n}\left\{\left(\sinh \left(\frac{n\pi }{a}(b-y)\right)+\sinh \left(\frac{n\pi }{a}y\right)\right)\frac{\sin \left(\frac{n\pi }{a}x\right)}{\sinh \left(\frac{n\pi }{a}b\right)}-\left(\sinh \left(\frac{n\pi }{b}(a-x)\right)+\sinh \left(\frac{n\pi }{b}x\right)\right)\frac{\sin \left(\frac{n\pi }{b}y\right)}{\sinh \left(\frac{n\pi }{b}a\right)}\right\}}}$

Definimos la función que calcula el potencial V(x,y), empleando N=100 términos del desarrollo en serie

function z = laplace_potencial_4(x,y, N, a, b)
    z=0;
    for n=0:N
        z1=(sinh((2*n+1)*pi*(a-x)/b)+sinh((2*n+1)*pi*x/b)).
*sin((2*n+1)*pi*y/b)/sinh((2*n+1)*pi*a/b);
        z2=(sinh((2*n+1)*pi*(b-y)/a)+sinh((2*n+1)*pi*y/a)).
*sin((2*n+1)*pi*x/a)/sinh((2*n+1)*pi*b/a);
        z=z+(z2-z1)*4/((2*n+1)*pi);
    end
end

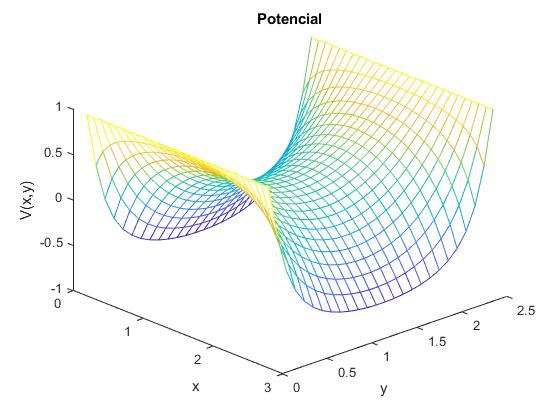
Representamos la función V(x,y) mediante mesh

m=5; %eje X
n=4; %eje Y
h=0.5; 
a=(m+1)*h;
b=(n+1)*h;
...
[x,y] = meshgrid(0:0.1:a, 0:0.1:b);
N=100;
z=laplace_potencial_4(x,y, N, a, b);
mesh(x,y,z)
xlabel('x')
ylabel('y')
zlabel('V(x,y)')
title('Potencial')

Unimos todas las porciones del script y comparamos el resultado analítico (puntos de color azul) y el numérico, (puntos de color rojo)

m=5; %eje X
n=4; %eje Y
h=0.5; 
a=(m+1)*h;
b=(n+1)*h;
%matriz V
A=zeros(n*m);
D=diag(4*ones(1,m))+diag(-1*ones(1,m-1),1)+diag(-1*ones(1,m-1),-1);
E=diag(-1*ones(1,m));
for i=0:n-1
    A(1+i*m:(i+1)*m,1+i*m:(i+1)*m)=D;
end
for i=1:n-1
    A(1+i*m:(i+1)*m,1+(i-1)*m:m*i)=E;
    A(1+(i-1)*m:i*m,1+i*m:(i+1)*m)=E;
end
%condiciones de contorno
VS=ones(1,m); %abajo
VN=ones(1,m); %arriba
VE=-ones(1,n); %derecha
VO=-ones(1,n); %izquierda
f=@(i,j) i+(j-1)*m;
%Vector términos
B=zeros(n*m,1);
%puntos rojos
B(f(1,1))=VO(1)+VS(1);
B(f(m,1))=VS(m)+VE(1);
B(f(1,n))=VN(1)+VO(n);
B(f(m,n))=VN(m)+VE(n);
%puntos verdes
for k=2:m-1
    B(f(k,1))=VS(k);
    B(f(k,n))=VN(k);
end
for k=2:n-1
    B(f(1,k))=VO(k);
    B(f(m,k))=VE(k);
end
X=A\B;
N=100;
g=@(x,y) laplace_potencial_4(x,y, N, a,b);
hold on
R=zeros(n,m);
for j=1:n
    for i=1:m
        k=f(i,j);
        R(n+1-j,i)=X(k);
        z=g(i*h,j*h);
        plot3(i*h,j*h,z,'o','markersize',3,'markeredgecolor',
'b','markerfacecolor','b')
        plot3(i*h,j*h,X(k),'o','markersize',3,'markeredgecolor',
'r','markerfacecolor','r')
    end
end
%comparación con la solución analítica
[x,y] = meshgrid(0:0.1:a, 0:0.1:b);
z=laplace_potencial_4(x,y, N, a, b);
mesh(x,y,z)
hold off
xlabel('x')
ylabel('y')
zlabel('V(x,y)')
title('Potencial')
view(47,32)

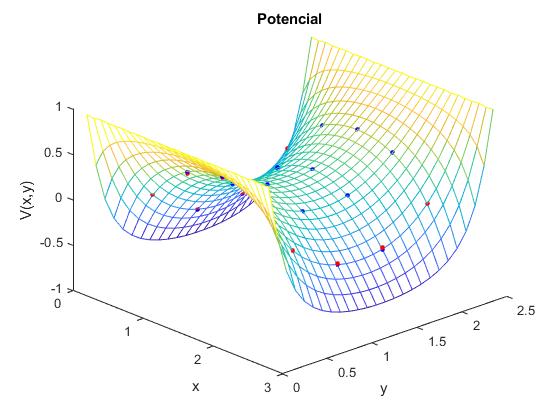
Comparación

La representación tridimensional no permite ver adecudamente, la comparación entre los resultados analíticos y numéricos.

• Representamos el potencial V(x_i,y), a lo largo de la línea x=x_i, paralela al eje Y y los comparamos con los cálculos numéricos,

• Representamos el potencial V(x,y_j), a lo largo de la línea y=y_j, paralela al eje X y los comparamos con los cálculos numéricos

Añadimos las siguientes líneas de código al script

...
figure
subplot(2,1,1)
gy=@(y) g(2*h,y);
hold on
fplot(gy,[0,b])
i=2;
for j=1:n
    k=f(i,j);
    line([j*h,j*h],[0,X(k)], 'color','r')
    plot(j*h,X(k),'o','markersize',3,'markeredgecolor','r',
'markerfacecolor','r')
end
hold off
grid on
xlabel('y')
ylabel('V(2h,y)')
title('Comparación')
subplot(2,1,2)
gx=@(x) g(x,2*h);
hold on
fplot(gx,[0,a])
j=2;
for i=1:m
    k=f(i,j);
    line([i*h,i*h],[0,X(k)], 'color','r')
    plot(i*h,X(k),'o','markersize',3,'markeredgecolor','r',
'markerfacecolor','r')
end
hold off
grid on
xlabel('x')
ylabel('V(x,2h)')
title('Comparación')

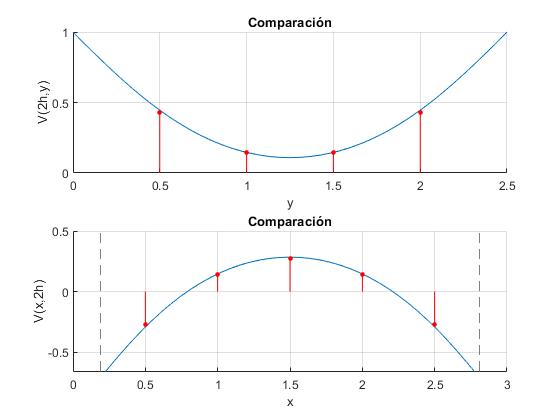
El procedimiento numérico se aproxima a la solución analítica, con muy pocos intervalos. Sin embargo, a medida que crece el número de intervalos, el número de ecuaciones se multiplica y el procedimiento directo resulta impracticable. Describimos un procedimiento iterativo, que conduce a la solución rápidamente.

Proceso iterativo

Consideremos un recinto rectangular de dimensiones a y b. Dividimos el eje X en m-1 intervalos, a=(m-1)h y el eje Y en n-1 intervalos, b=(n-1)h

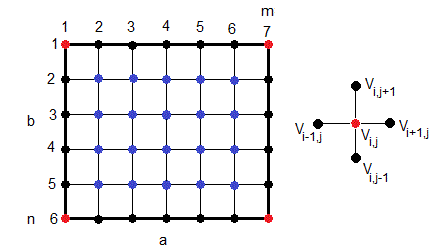
Conocidos los potenciales en los bordes, V_i,1, V_i,m, (i=2,...n-1), V_1,j, V_n,j, (j=2,...m-1), en color negro, calcularemos los potenciales V_i,j en los puntos del interior, en color azul, (i=2...n-1, j=2,...m-1).

Como hemos visto, el potencial V_i,j del punto (i,j) se calcula a partir de los potenciales de los cuatro más próximos, tal como se muestra en la figura de la derecha,

${\displaystyle 4V_{i,j}^{k+1}=V_{i+\mathrm{1,}j}^k+V_{i-\mathrm{1,}j}^k+V_{i,j+1}^k+V_{i,j-1}^k}$

El superíndice k se refiere al valor del potencial de los puntos interiores V_i,j en en la iteracción k. k=0, se refiere al valor inicial del potencial de los puntos interiores

El proceso iterativo concluye cuando se alcanza un máximo número de iteracciones o cuando el error relativo definido para cada uno de los puntos interiores i,j es menor que una cantidad fijada ε

${\displaystyle \left|\frac{V_{i,j}^{k+1}-V_{i,j}^k}{V_{i,j}^{k+1}}\right|<\epsilon }$

Declaramos una matriz V0, de n filas y n columnas. Establecemos sus valores fijos en los bordes (negros) y un valor inicial (cero) en los puntos (i,j) del interior (azules)

m=7; %columnas
n=6; %filas
V0=zeros(n,m);
%condiciones de contorno
for i=2:n-1 %izquierda/derecha
    V0(i,1)=-1;
    V0(i,m)=-1;
end
for j=2:m-1 %arriba/abajo
    V0(1,j)=1;
    V0(n,j)=1;
end

Asignamos a los vértices, puntos de color rojo, el valor medio del potencial de los dos puntos más proximos de los bordes

${\displaystyle \begin{array}{l}{V}_{\mathrm{1,1}}=\frac{1}{2}\left(V_{\mathrm{1,2}}+V_{\mathrm{2,1}}\right)\\ V_{n\mathrm{,1}}=\frac{1}{2}\left(V_{n-\mathrm{1,1}}+V_{n\mathrm{,2}}\right)\\ V_{\mathrm{1,}m}=\frac{1}{2}\left(V_{\mathrm{1,}m-1}+V_{\mathrm{2,}m}\right)\\ V_{n,m}=\frac{1}{2}\left(V_{n-\mathrm{1,}m}+V_{n,m-1}\right)\end{array}}$

%las cuatro esquinas
 V0(1,1)=(V0(1,2)+V0(2,1))/2;
 V0(n,1)=(V0(n-1,1)+V0(n,2))/2;
 V0(1,m)=(V0(1,m-1)+V0(2,m))/2;
 V0(n,m)=(V0(n-1,m)+V0(n,m-1))/2;

El proceso iterativo es muy fácil de programar, para ello declaramos una matriz V de la misma dimensión que V0, que va a guardar los potenciales de los puntos interiores y los fijos de los bordes, en la iteracción k+1

...
V=V0;
N=100; %máximo número de iteracciones
for k=1:N
    contador=0;
    for i=2:n-1
        for j=2:m-1
            V(i,j)=(V0(i+1,j)+V0(i-1,j)+V0(i,j-1)+V0(i,j+1))/4;
            error=abs((V(i,j)-V0(i,j))/V(i,j));
            if error<0.0001
                contador=contador+1;
            end
        end
    end
    if contador==(n-2)*(m-2) %termina el proceso iterativo
        break;
     end
    V0=V;
end

Unimos las porciones de código, para crear el script

m=7; %columnas
n=6; %filas
V0=zeros(n,m);
%condiciones de contorno
for i=2:n-1 %izquierda/derecha
    V0(i,1)=-1;
    V0(i,m)=-1;
end
for j=2:m-1 %arriba/abajo
    V0(1,j)=1;
    V0(n,j)=1;
end
%las cuatro esquinas
V0(1,1)=(V0(1,2)+V0(2,1))/2;
V0(n,1)=(V0(n-1,1)+V0(n,2))/2;
V0(1,m)=(V0(1,m-1)+V0(2,m))/2;
V0(n,m)=(V0(n-1,m)+V0(n,m-1))/2;

%proceso ierativo
V=V0;
N=100; %máximo número de iteracciones
for k=1:N
    contador=0;
    for i=2:n-1
        for j=2:m-1
            V(i,j)=(V0(i+1,j)+V0(i-1,j)+V0(i,j-1)+V0(i,j+1))/4;
            error=abs((V(i,j)-V0(i,j))/V(i,j));
            if error<0.0001
                contador=contador+1;
            end
        end
    end
    if contador==(n-2)*(m-2) %termina el proceso iterativo
        break;
     end
    V0=V;
end
if k==N
    disp('Se ha superado el máximo número de iteracciones')
else
        disp(V(2:n-1,2:m-1)) %puntos interiores
end

El resultado como podemos apreciar es muy parecido al obtenido medinte el procedimiento directo. Véase la matriz R de los potenciales de los puntos interiores en el apartado anterior

    0.0389    0.4285    0.5324    0.4285    0.0389
   -0.2728    0.1428    0.2727    0.1428   -0.2728
   -0.2728    0.1428    0.2727    0.1428   -0.2728
    0.0389    0.4285    0.5324    0.4285    0.0389

El procedimiento iterativo se termina cuando el número de iteracciones k=47. El procedimiento se puede mejorar introduciendo una combinación lineal de V0 (iteraccion k) y V (iteraccion k+1)