La ecuación de Laplace en coordenadas rectangulares es

${\displaystyle \frac{{\partial }^{2}V}{\partial x^2}+\frac{{\partial }^{2}V}{\partial y^2}+\frac{{\partial }^{2}V}{\partial z^2}=0}$

Conocido el potencial eléctrico V(x,y,z) calculamos el vector campo eléctrico en el punto (x,y,z mediante

${\displaystyle \overrightarrow{E}=-\frac{\partial V}{\partial x}\widehat{i}-\frac{\partial V}{\partial y}\widehat{j}-\frac{\partial V}{\partial z}\widehat{k}}$

Separando las variables, es posible encontrar una solución a la ecuación de Laplace que satisfaga las condiciones de contorno. V(x,y,z)=X(x)·Y(y)·Z(z)

${\displaystyle \begin{array}{l}Y(y)Z(z)\frac{d^{2}X(x)}{d{x}^2}+X(x)Z(z)\frac{d^{2}Y(y)}{d{y}^2}+X(x)Y(y)\frac{d^{2}Z(z)}{d{z}^2}=0\\ \frac{1}{X(x)}\frac{d^{2}X(x)}{d{x}^2}+\frac{1}{Y(y)}\frac{d^{2}Y(y)}{d{y}^2}+\frac{1}{Z(z)}\frac{d^{2}Z(z)}{d{z}^2}=0\end{array}}$

Se tiene qe cumplir para cualquier x, y y z

${\displaystyle \begin{array}{l}\frac{1}{X(x)}\frac{d^{2}X(x)}{d{x}^2}=-k_x^2\\ \frac{1}{Y(y)}\frac{d^{2}Y(y)}{d{y}^2}=-k_y^2\\ \frac{1}{Z(z)}\frac{d^{2}Z(z)}{d{z}^2}=-k_z^2\end{array}\}{k}_x^2+k_y^2+k_z^2=0}$

Estudiaremos aquellas situaciones que no dependan de la variable z. Por lo que

${\displaystyle k_x^2+k_y^2=\mathrm{0,}-k_x^2=k_y^2=k^2}$

Tendremos dos posibles soluciones

• Oscilatoria a lo largo del eje Y, exponencial a lo largo del eje X

${\displaystyle \begin{array}{l}\begin{array}{l}\frac{d^{2}X(x)}{d{x}^2}-k^{2}X(x)=0\\ \frac{d^{2}Y(y)}{d{y}^2}+k^{2}Y(y)=0\end{array}\}\\ \{\begin{array}{l}X(x)=A\text{'}\exp (-kx)+B\text{'}\exp (kx)=A\sinh (kx)+B\cosh (kx)\\ Y(y)=C\sin (ky)+D\cos (ky)\end{array}\end{array}}$

• Oscilatoria a lo largo del eje X, exponencial a lo largo del eje Y

${\displaystyle \begin{array}{l}\begin{array}{l}\frac{d^{2}X(x)}{d{x}^2}+k^{2}X(x)=0\\ \frac{d^{2}Y(y)}{d{y}^2}-k^{2}Y(y)=0\end{array}\}\\ \{\begin{array}{l}X(x)=A\sin (kx)+B\cos (kx)\\ Y(y)=C\sinh (ky)+D\cosh (ky)\end{array}\end{array}}$

Ejemplo

Consideremos dos placas de anchura a infintimante largas paralelas al plano XZ, conectadas a tierra, su potencial V=0. Otras dos placas de anchura b infintimante largas paralelas al plano YZ, el potencial de la primera es V₁ y el de la segunda V₂

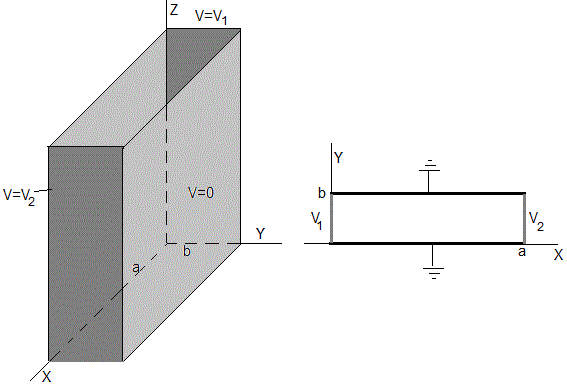
Cortando las cuatro placas por un plano perpendicular al eje Z, obtenemos el recinto rectangular, que se muestra en la figura de la derecha

La solución de la ecuación de Laplace es el producto V(x,y)=X(x)·Y(y)

${\displaystyle \begin{array}{l}X(x)=A\sinh (kx)+B\cosh (kx)\\ Y(y)=C\sin (ky)+D\cos (ky)\end{array}}$

Los coeficientes se calculan a partir de las condiciones de contorno

${\displaystyle \{\begin{array}{l}V(x\mathrm{,0})=0\\ V(x,b)=0\\ V(\mathrm{0,}y)=V_1\\ V(a,y)=V_2\end{array}}$

La primera condición hace que D=0, y para que el potencial V(x,b)=0, se anule en y=b, se tiene que cumplir que kb=nπ (n=1,2,3...). En consecuencia

${\displaystyle Y(y)=C\sin \left(\frac{n\pi }{b}y\right)}$

El potencial V(x,y) en cualuquier punto del recinto rectangular 0≤x≤a, 0≤y≤b, es la superposición

${\displaystyle V(x,y)={\displaystyle \sum _{n=1}^{\infty }\left(A_n\sinh \left(\frac{n\pi }{b}x\right)+B_n\cosh \left(\frac{n\pi }{b}x\right)\right)\sin \left(\frac{n\pi }{b}y\right)}}$

En x=0, se cumple V(0,y)=V₁

${\displaystyle V(\mathrm{0,}y)=V_1={\displaystyle \sum _{n=1}^{\infty }{B}_n\sin \left(\frac{n\pi }{b}y\right)}}$

Utilizando el procedimiento para calcular los coeficientes del desarrollo en serie de Fourier de una función periódica

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{b}{\int }}{V}_1\sin \left(\frac{m\pi }{b}y\right)dy}={\displaystyle \underset{0}{\overset{b}{\int }}\left\{{\displaystyle \sum _{n=1}^{\infty }{B}_n\sin \left(\frac{n\pi }{b}y\right)\sin \left(\frac{m\pi }{b}y\right)}\right\}dy}\\ V_1{\displaystyle \underset{0}{\overset{b}{\int }}\sin \left(\frac{m\pi }{b}y\right)dy}={\displaystyle \sum _{n=1}^{\infty }{B}_n{\displaystyle \underset{0}{\overset{b}{\int }}\left\{\sin \left(\frac{n\pi }{b}y\right)\sin \left(\frac{m\pi }{b}y\right)\right\}dy}}\end{array}}$

y las relaciones trigonométricas

${\displaystyle \begin{array}{l}\sin A·\sin B=\frac{1}{2}\left(\cos (A-B)-\cos (A+B)\right)\\ {\sin }^{2}A=\frac{1}{2}\left(1-\cos (2A)\right)\end{array}}$

El resultado de las integrales es

${\displaystyle \begin{array}{l}{V}_1{\displaystyle \underset{0}{\overset{b}{\int }}\sin \left(\frac{m\pi }{b}y\right)dy}=\{\begin{array}{l}\frac{2b}{m\pi }{V}_1,m\text{impar}\\ \mathrm{0,}m\text{par}\end{array}\\ B_n{\displaystyle \underset{0}{\overset{b}{\int }}\left\{\sin \left(\frac{n\pi }{b}y\right)\sin \left(\frac{m\pi }{b}y\right)\right\}dy}=\{\begin{array}{l}\mathrm{0,}m\ne n\\ B_n\frac{b}{2},m=n\end{array}\end{array}}$

Los coeficientes B_n valen

${\displaystyle B_n=\{\begin{array}{l}\frac{4V_1}{n\pi },n\text{impar}\\ \mathrm{0,}n\text{par}\end{array}}$

La otra condición de contorno en x=a es V(a,y)=V₂

${\displaystyle V(a,y)=V_2={\displaystyle \sum _{n=1}^{\infty }\left(A_n\sinh \left(\frac{n\pi }{b}a\right)+B_n\cosh \left(\frac{n\pi }{b}a\right)\right)\sin \left(\frac{n\pi }{b}y\right)}}$

Obtenemos A_nsinh(nπa/b)+B_ncosh(nπa/b) por el mismo procedimiento

${\displaystyle A_n\sinh \left(\frac{n\pi }{b}a\right)+B_n\cosh \left(\frac{n\pi }{b}a\right)=\{\begin{array}{l}\frac{4V_2}{n\pi },n\text{impar}\\ \mathrm{0,}n\text{par}\end{array}}$

Despejamos A_n conocido B_n. El potencial V(x,y) en cualquier punto (x,y) de la región rectangular es

${\displaystyle \begin{array}{l}V(x,y)={\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\left(A_n\sinh \left(\frac{n\pi }{b}x\right)+B_n\cos \left(\frac{n\pi }{b}x\right)\right)\sin \left(\frac{n\pi }{b}y\right)}\\ A_n=\frac{4}{n\pi }\frac{V_2-V_1\cosh \left(\frac{n\pi }{b}a\right)}{\sinh \left(\frac{n\pi }{b}a\right)}\\ B_n=\frac{4}{n\pi }{V}_1\end{array}}$

Teniendo en cuenta que sinh(A-B)=sinh(A)cosh(B)-sinh(B)cosh(A), llegamos a una expresión más compacta para el potencial V(x,y)

${\displaystyle V(x,y)=\frac{4}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{1}{n}\left(\frac{V_2\sinh \left(\frac{n\pi }{b}x\right)+V_1\sinh \left(\frac{n\pi }{b}(a-x)\right)}{\sinh \left(\frac{n\pi }{b}a\right)}\right)\sin \left(\frac{n\pi }{b}y\right)}}$

Ejemplo

• a=1
• b=1
• V₁=1
• V₂=0

Definimos la función que calcula el potencial V(x,y), empleando N=100 términos del desarrollo en serie

function z = laplace_potencial_3(x,y, N, V1, V2, a, b)
    z=0;
    for n=1:N
    z=z+4*(V2*sinh((2*n-1)*pi*x/b)+V1*sinh((2*n-1)*pi*(a-x)/b)).
*sin((2*n-1)*pi*y/b)/(sinh((2*n-1)*pi*a/b)*(2*n-1)*pi);
    end
end

Representamos las líneas equipotenciales mediante fcontour

V1=1; %potenciales
V2=0;
a=1; %dimensiones 
b=1;
N=100;
f=@(x,y) laplace_potencial_3(x,y, N, V1, V2, a, b);
fcontour(f,[0,a,0,b], 'fill','on')
colorbar
xlabel('x')
ylabel('y')
title('V(x,y)')

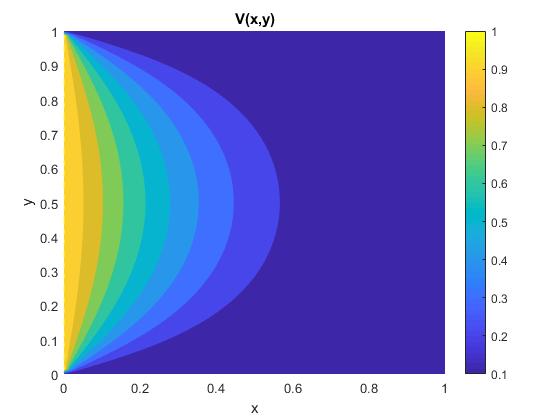
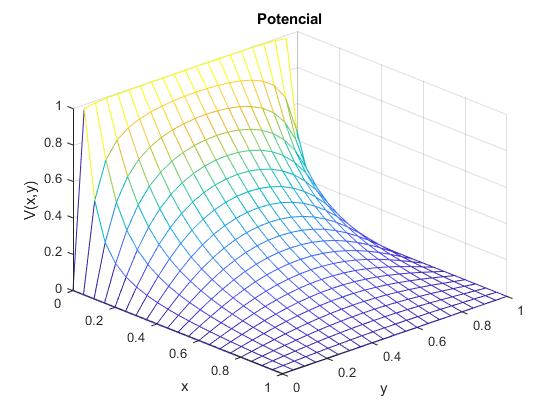
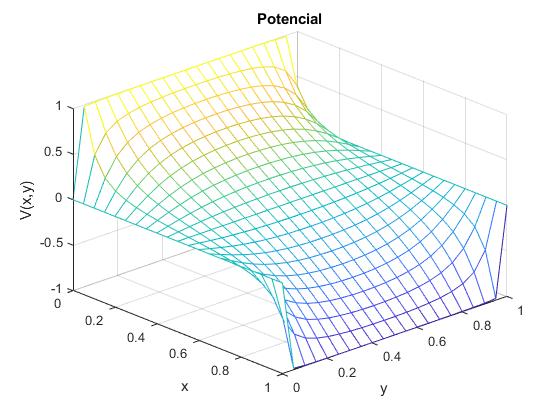
Representamos la función V(x,y) mediante mesh

a=1;
b=1;
[x,y] = meshgrid(0:0.05:a, 0:0.05:b);
N=100;
V1=1;
V2=0;
z=laplace_potencial_3(x,y, N, V1, V2, a, b);
mesh(x,y,z)
xlabel('x')
ylabel('y')
zlabel('V(x,y)')
title('Potencial')
view(47,32)

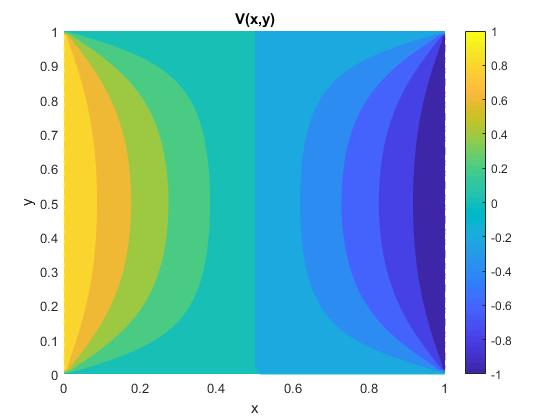
Cambiamos el valor de V₂=-1

Caso general

Utilizando el principio de superposición resolvemos la ecuación de Laplace para el caso general con las condiciones de contorno se especifican en la figura de la izquierda.

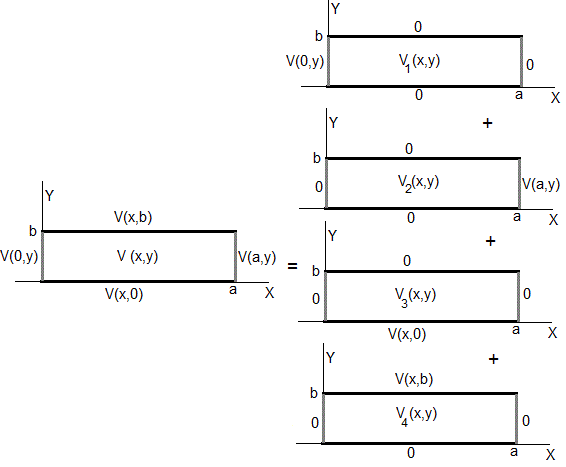
El potencial en un punto (x,y) del rectángulo de dimensiones a y b es la suma de las cuatro contribuciones, V(x,y)=V₁(x,y)+V₂(x,y)+V₃(x,y)+V₄(x,y)

Calculamos cada una de las contribuciones

1. Potencial V₁(x,y)



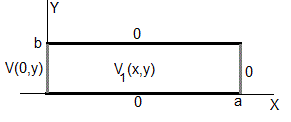
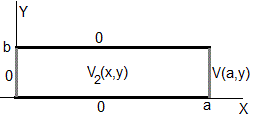
La solución es oscilatoria a lo largo del eje Y, exponencial a lo largo del eje X

${\displaystyle \begin{array}{l}X(x)=A\sinh (kx)+B\cosh (kx)\\ Y(y)=C\sin (ky)+D\cos (ky)\end{array}}$

La condición de contorno V(x,0)=0, hace que D=0, la condición de contorno V(x,b)=0, hace que kb=nπ (n=1,2,3...). En consecuencia

${\displaystyle Y(y)=C\sin \left(\frac{n\pi }{b}y\right)}$

El potencial V₁(x,y) en cualquier punto del recinto rectangular 0≤x≤a, 0≤y≤b, es la superposición

${\displaystyle V_1(x,y)={\displaystyle \sum _{n=1}^{\infty }\left(A_n\sinh \left(\frac{n\pi }{b}x\right)+B_n\cosh \left(\frac{n\pi }{b}x\right)\right)\sin \left(\frac{n\pi }{b}y\right)}}$

En x=0, se cumple

${\displaystyle V(\mathrm{0,}y)={\displaystyle \sum _{n=1}^{\infty }{B}_n\sin \left(\frac{n\pi }{b}y\right)}}$

Utilizando el procedimiento para calcular los coeficientes del desarrollo en serie de Fourier de una función periódica

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{b}{\int }}V(\mathrm{0,}y)\sin \left(\frac{m\pi }{b}y\right)dy}={\displaystyle \underset{0}{\overset{b}{\int }}\left\{{\displaystyle \sum _{n=1}^{\infty }{B}_n\sin \left(\frac{n\pi }{b}y\right)\sin \left(\frac{m\pi }{b}y\right)}\right\}dy}\\ {\displaystyle \underset{0}{\overset{b}{\int }}V(\mathrm{0,}y)\sin \left(\frac{m\pi }{b}y\right)dy}={\displaystyle \sum _{n=1}^{\infty }{B}_n{\displaystyle \underset{0}{\overset{b}{\int }}\left\{\sin \left(\frac{n\pi }{b}y\right)\sin \left(\frac{m\pi }{b}y\right)\right\}dy}}\\ {\displaystyle \underset{0}{\overset{b}{\int }}V(\mathrm{0,}y)\sin \left(\frac{m\pi }{b}y\right)dy}=\frac{b}{2}{B}_m\end{array}}$

La otra condición de contorno en x=a es V(a,y)=0

${\displaystyle \begin{array}{l}V(a,y)=0={\displaystyle \sum _{n=1}^{\infty }\left(A_n\sinh \left(\frac{n\pi }{b}a\right)+B_n\cosh \left(\frac{n\pi }{b}a\right)\right)\sin \left(\frac{n\pi }{b}y\right)}\\ A_n\sinh \left(\frac{n\pi }{b}a\right)+B_n\cosh \left(\frac{n\pi }{b}a\right)=0\\ A_n=-B_n\frac{\cosh \left(\frac{n\pi }{b}a\right)}{\sinh \left(\frac{n\pi }{b}a\right)}\end{array}}$

El potencial V₁(x,y) en cualquier punto (x,y) de la región rectangular es

${\displaystyle V_1(x,y)={\displaystyle \sum _{n=1}^{\infty }\left(A_n\sinh \left(\frac{n\pi }{b}x\right)+B_n\cosh \left(\frac{n\pi }{b}x\right)\right)\sin \left(\frac{n\pi }{b}y\right)}}$

Teniendo en cuenta que sinh(A-B)=sinh(A)cosh(B)-sinh(B)cosh(A), llegamos a una expresión más compacta para el potencial V₁(x,y)

${\displaystyle V_1(x,y)=\frac{2}{b}{\displaystyle \sum _{n=1}^{\infty }\left({\displaystyle \underset{0}{\overset{b}{\int }}V(\mathrm{0,}y)\sin \left(\frac{n\pi }{b}y\right)dy}\left\{\frac{\sinh \left(\frac{n\pi }{b}(a-x)\right)}{\sinh \left(\frac{n\pi }{b}a\right)}\right\}\sin \left(\frac{n\pi }{b}y\right)\right)}}$

2. Potencial V₂(x,y)



La solución es oscilatoria a lo largo del eje Y, exponencial a lo largo del eje X

${\displaystyle \begin{array}{l}X(x)=A\sinh (kx)+B\cosh (kx)\\ Y(y)=C\sin (ky)+D\cos (ky)\end{array}}$

La condición de contorno V(x,0)=0, hace que D=0, la condición de contorno V(x,b)=0, hace que kb=nπ (n=1,2,3...). En consecuencia

${\displaystyle Y(y)=C\sin \left(\frac{n\pi }{b}y\right)}$

El potencial V₂(x,y) en cualquier punto del recinto rectangular 0≤x≤a, 0≤y≤b, es la superposición

${\displaystyle V_2(x,y)={\displaystyle \sum _{n=1}^{\infty }\left(A_n\sinh \left(\frac{n\pi }{b}x\right)+B_n\cosh \left(\frac{n\pi }{b}x\right)\right)\sin \left(\frac{n\pi }{b}y\right)}}$

En x=0, se cumple

${\displaystyle V(\mathrm{0,}y)=0={\displaystyle \sum _{n=1}^{\infty }{B}_n\sin \left(\frac{n\pi }{b}y\right)}}$

Por lo que B_n=0

La otra condición de contorno en x=a es V(a,y)

${\displaystyle V(a,y)={\displaystyle \sum _{n=1}^{\infty }\left(A_n\sinh \left(\frac{n\pi }{b}a\right)\right)\sin \left(\frac{n\pi }{b}y\right)}}$

Empleando el procedimiento para calcular los coeficientes del desarrollo en serie de Fourier de una función periódica

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{b}{\int }}V(a,y)\sin \left(\frac{m\pi }{b}y\right)dy}={\displaystyle \underset{0}{\overset{b}{\int }}\left\{{\displaystyle \sum _{n=1}^{\infty }{A}_n\sinh \left(\frac{n\pi }{b}a\right)\sin \left(\frac{n\pi }{b}y\right)\sin \left(\frac{m\pi }{b}y\right)}\right\}dy}\\ {\displaystyle \underset{0}{\overset{b}{\int }}V(a,y)\sin \left(\frac{m\pi }{b}y\right)dy}={\displaystyle \sum _{n=1}^{\infty }{A}_n\sinh \left(\frac{n\pi }{b}a\right){\displaystyle \underset{0}{\overset{b}{\int }}\left\{\sin \left(\frac{n\pi }{b}y\right)\sin \left(\frac{m\pi }{b}y\right)\right\}dy}}\\ {\displaystyle \underset{0}{\overset{b}{\int }}V(a,y)\sin \left(\frac{m\pi }{b}y\right)dy}=\frac{b}{2}{A}_n\sinh \left(\frac{m\pi }{b}a\right)\end{array}}$

El potencial V₂(x,y) en cualquier punto (x,y) de la región rectangular es

${\displaystyle V_2(x,y)={\displaystyle \sum _{n=1}^{\infty }\left(A_n\sinh \left(\frac{n\pi }{b}x\right)\right)\sin \left(\frac{n\pi }{b}y\right)}}$

Conocido A_n, la expresión final es

${\displaystyle V_2(x,y)=\frac{2}{b}{\displaystyle \sum _{n=1}^{\infty }\left({\displaystyle \underset{0}{\overset{b}{\int }}V(a,y)\sin \left(\frac{n\pi }{b}y\right)dy}\left\{\frac{\sinh \left(\frac{n\pi }{b}x\right)}{\sinh \left(\frac{n\pi }{b}a\right)}\right\}\sin \left(\frac{n\pi }{b}y\right)\right)}}$

3. Potencial V₃(x,y)



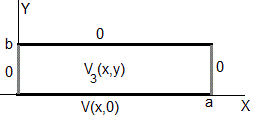
La solución es oscilatoria a lo largo del eje X, exponencial a lo largo del eje Y

${\displaystyle \begin{array}{l}X(x)=A\sin (kx)+B\cos (kx)\\ Y(y)=C\sinh (ky)+D\cosh (ky)\end{array}}$

La condición de contorno V(0, y)=0, hace que B=0, la condición de contorno V(a,y)=0, hace que ka=nπ (n=1,2,3...). En consecuencia

${\displaystyle X(x)=A\sin \left(\frac{n\pi }{a}x\right)}$

El potencial V₃(x,y) en cualquier punto del recinto rectangular 0≤x≤a, 0≤y≤b, es la superposición

${\displaystyle V_3(x,y)={\displaystyle \sum _{n=1}^{\infty }\left(C_n\sinh \left(\frac{n\pi }{a}y\right)+D_n\cosh \left(\frac{n\pi }{a}y\right)\right)\sin \left(\frac{n\pi }{a}x\right)}}$

En y=0, se cumple

${\displaystyle V(x\mathrm{,0})={\displaystyle \sum _{n=1}^{\infty }{D}_n\sin \left(\frac{n\pi }{a}x\right)}}$

Utilizando el procedimiento para calcular los coeficientes del desarrollo en serie de Fourier de una función periódica

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{a}{\int }}V(x\mathrm{,0})\sin \left(\frac{m\pi }{a}x\right)dx}={\displaystyle \underset{0}{\overset{a}{\int }}\left\{{\displaystyle \sum _{n=1}^{\infty }{D}_n\sin \left(\frac{n\pi }{a}x\right)\sin \left(\frac{m\pi }{a}x\right)}\right\}dx}\\ {\displaystyle \underset{0}{\overset{a}{\int }}V(x\mathrm{,0})\sin \left(\frac{m\pi }{a}x\right)dx}={\displaystyle \sum _{n=1}^{\infty }{D}_n{\displaystyle \underset{0}{\overset{a}{\int }}\left\{\sin \left(\frac{n\pi }{a}x\right)\sin \left(\frac{m\pi }{a}x\right)\right\}dy}}\\ {\displaystyle \underset{0}{\overset{a}{\int }}V(x\mathrm{,0})\sin \left(\frac{m\pi }{a}x\right)dx}=\frac{a}{2}{D}_m\end{array}}$

La otra condición de contorno es y=b es, V(x,b)=0

${\displaystyle \begin{array}{l}V(x,b)=0={\displaystyle \sum _{n=1}^{\infty }\left(C_n\sinh \left(\frac{n\pi }{a}b\right)+D_n\cosh \left(\frac{n\pi }{a}b\right)\right)\sin \left(\frac{n\pi }{a}x\right)}\\ C_n\sinh \left(\frac{n\pi }{a}b\right)+D_n\cosh \left(\frac{n\pi }{a}b\right)=0\\ C_n=-D_n\frac{\cosh \left(\frac{n\pi }{a}b\right)}{\sinh \left(\frac{n\pi }{a}b\right)}\end{array}}$

El potencial V₃(x,y) en cualquier punto (x,y) de la región rectangular es

${\displaystyle V_3(x,y)={\displaystyle \sum _{n=1}^{\infty }\left(C_n\sinh \left(\frac{n\pi }{a}y\right)+D_n\cosh \left(\frac{n\pi }{a}y\right)\right)\sin \left(\frac{n\pi }{a}x\right)}}$

Teniendo en cuenta que sinh(A-B)=sinh(A)cosh(B)-sinh(B)cosh(A), llegamos a una expresión más compacta para el potencial V₃(x,y)

${\displaystyle V_3(x,y)=\frac{2}{a}{\displaystyle \sum _{n=1}^{\infty }\left({\displaystyle \underset{0}{\overset{a}{\int }}V(x\mathrm{,0})\sin \left(\frac{n\pi }{a}x\right)dx}\left\{\frac{\sinh \left(\frac{n\pi }{a}(b-y)\right)}{\sinh \left(\frac{n\pi }{a}b\right)}\right\}\sin \left(\frac{n\pi }{a}x\right)\right)}}$

4. Potencial V₄(x,y)



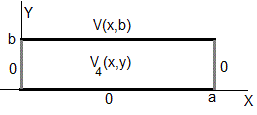
La solución es oscilatoria a lo largo del eje X, exponencial a lo largo del eje Y

${\displaystyle \begin{array}{l}X(x)=A\sin (kx)+B\cos (kx)\\ Y(y)=C\sinh (ky)+D\cosh (ky)\end{array}}$

La condición de contorno V(0, y)=0, hace que B=0, la condición de contorno V(a,y)=0, hace que ka=nπ (n=1,2,3...). En consecuencia

${\displaystyle X(x)=A\sin \left(\frac{n\pi }{a}x\right)}$

El potencial V₄(x,y) en cualquier punto del recinto rectangular 0≤x≤a, 0≤y≤b, es la superposición

${\displaystyle V_4(x,y)={\displaystyle \sum _{n=1}^{\infty }\left(C_n\sinh \left(\frac{n\pi }{a}y\right)+D_n\cosh \left(\frac{n\pi }{a}y\right)\right)\sin \left(\frac{n\pi }{a}x\right)}}$

En y=0, se cumple

${\displaystyle V(x\mathrm{,0})=0={\displaystyle \sum _{n=1}^{\infty }{D}_n\sin \left(\frac{n\pi }{a}x\right)}}$

Por lo que D_n=0

La otra condición de contorno en y=b es V(x,b)

${\displaystyle V(x,b)={\displaystyle \sum _{n=1}^{\infty }\left(C_n\sinh \left(\frac{n\pi }{a}b\right)\right)\sin \left(\frac{n\pi }{a}x\right)}}$

Utilizando el procedimiento para calcular los coeficientes del desarrollo en serie de Fourier de una función periódica

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{a}{\int }}V(x,b)\sin \left(\frac{m\pi }{a}x\right)dx}={\displaystyle \underset{0}{\overset{a}{\int }}\left\{{\displaystyle \sum _{n=1}^{\infty }{C}_n\sinh \left(\frac{n\pi }{a}b\right)\sin \left(\frac{n\pi }{a}x\right)\sin \left(\frac{m\pi }{a}x\right)}\right\}dx}\\ {\displaystyle \underset{0}{\overset{a}{\int }}V(x,b)\sin \left(\frac{m\pi }{a}x\right)dx}={\displaystyle \sum _{n=1}^{\infty }{C}_n\sinh \left(\frac{n\pi }{a}b\right){\displaystyle \underset{0}{\overset{a}{\int }}\left\{\sin \left(\frac{n\pi }{a}x\right)\sin \left(\frac{m\pi }{a}x\right)\right\}dx}}\\ {\displaystyle \underset{0}{\overset{a}{\int }}V(x,b)\sin \left(\frac{m\pi }{a}x\right)dx}=\frac{a}{2}{C}_n\sinh \left(\frac{m\pi }{a}b\right)\end{array}}$

El potencial V₄(x,y) en cualquier punto (x,y) de la región rectangular es

${\displaystyle V_4(x,y)={\displaystyle \sum _{n=1}^{\infty }\left(C_n\sinh \left(\frac{n\pi }{a}y\right)\right)\sin \left(\frac{n\pi }{a}x\right)}}$

Conocido C_n, la expresión final es

${\displaystyle V_4(x,y)=\frac{2}{a}{\displaystyle \sum _{n=1}^{\infty }\left({\displaystyle \underset{0}{\overset{a}{\int }}V(x,b)\sin \left(\frac{n\pi }{a}x\right)dx}\left\{\frac{\sinh \left(\frac{n\pi }{a}y\right)}{\sinh \left(\frac{n\pi }{a}b\right)}\right\}\sin \left(\frac{n\pi }{a}x\right)\right)}}$

Ejemplo

Podríamos deducir la expresión del potencial V(x,y) del ejemplo 1, a partir del caso general. Las condiciones de contorno V(0,y)=V₁, V(a,y)=V₂, V(x,0)=0, V(x,b)=0, dan lugar al potencial V(x,y)=V₁(x,y)+V₂(x,y)

${\displaystyle \begin{array}{l}{V}_1(x,y)=\frac{2}{b}{\displaystyle \sum _{n=1}^{\infty }\left({\displaystyle \underset{0}{\overset{b}{\int }}V(\mathrm{0,}y)\sin \left(\frac{n\pi }{b}y\right)dy}\left\{\frac{\sinh \left(\frac{n\pi }{b}(a-x)\right)}{\sinh \left(\frac{n\pi }{b}a\right)}\right\}\sin \left(\frac{n\pi }{b}y\right)\right)}=\frac{4V_1}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5..}}^{\infty }\left(\frac{1}{n}\left\{\frac{\sinh \left(\frac{n\pi }{b}(a-x)\right)}{\sinh \left(\frac{n\pi }{b}a\right)}\right\}\sin \left(\frac{n\pi }{b}y\right)\right)}\\ V_2(x,y)=\frac{2}{b}{\displaystyle \sum _{n=1}^{\infty }\left({\displaystyle \underset{0}{\overset{b}{\int }}V(a,y)\sin \left(\frac{n\pi }{b}y\right)dy}\left\{\frac{\sinh \left(\frac{n\pi }{b}x\right)}{\sinh \left(\frac{n\pi }{b}a\right)}\right\}\sin \left(\frac{n\pi }{b}y\right)\right)}=\frac{4V_2}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\left(\frac{1}{n}\left\{\frac{\sinh \left(\frac{n\pi }{b}x\right)}{\sinh \left(\frac{n\pi }{b}a\right)}\right\}\sin \left(\frac{n\pi }{b}y\right)\right)}\end{array}}$

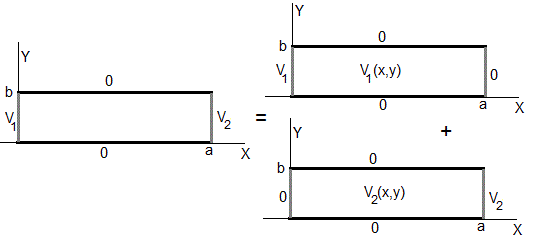
Otras condiciones de contorno

En este apartado, estudiamos condiciones de contorno definidas por la derivada primera de V, respecto de x o respecto de y. Consideremos el ejemplo de la figura, la derivada del potencial V(x,y) con respecto a x es nula en x=a

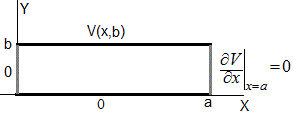
La solución es oscilatoria a lo largo del eje X, exponencial a lo largo del eje Y

${\displaystyle \begin{array}{l}X(x)=A\sin (kx)+B\cos (kx)\\ Y(y)=C\sinh (ky)+D\cosh (ky)\end{array}}$

La condición de contorno V(0,y)=0 hacen que B=0. La condición

${\displaystyle {\frac{\partial X}{\partial x}|}_{x=a}=Ak\cos (ka)=0}$

hacen que ka=(2n+1)π/2, (n=0,1,2,3...). En consecuencia

${\displaystyle X(x)=A\sin \left(\frac{(2n+1)\pi }{2a}x\right)}$

El potencial V(x,y) en cualquier punto del recinto rectangular 0≤x≤a, 0≤y≤b, es la superposición

${\displaystyle V(x,y)={\displaystyle \sum _{n=0}^{\infty }\left(C_n\sinh \left(\frac{(2n+1)\pi }{2a}y\right)+D_n\cosh \left(\frac{(2n+1)\pi }{2a}y\right)\right)\sin \left(\frac{(2n+1)\pi }{2a}x\right)}}$

En y=0, se cumple

${\displaystyle V(x\mathrm{,0})=0={\displaystyle \sum _{n=0}^{\infty }{D}_n\sin \left(\frac{(2n+1)\pi }{2a}x\right)}}$

Por lo que D_n=0

La otra condición de contorno en y=b es V(x,b)

${\displaystyle V(x,b)={\displaystyle \sum _{n=0}^{\infty }\left(C_n\sinh \left(\frac{(2n+1)\pi }{2a}b\right)\right)\sin \left(\frac{(2n+1)\pi }{2a}x\right)}}$

Utilizando el procedimiento para calcular los coeficientes del desarrollo en serie de Fourier de una función periódica

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{a}{\int }}V(x,b)\sin \left(\frac{(2m+1)\pi }{2a}x\right)dx}={\displaystyle \underset{0}{\overset{a}{\int }}\left\{{\displaystyle \sum _{n=0}^{\infty }{C}_n\sinh \left(\frac{(2n+1)\pi }{2a}b\right)\sin \left(\frac{(2n+1)\pi }{2a}x\right)\sin \left(\frac{(2m+1)\pi }{2a}x\right)}\right\}dx}\\ {\displaystyle \underset{0}{\overset{a}{\int }}V(x,b)\sin \left(\frac{(2m+1)\pi }{2a}x\right)dx}={\displaystyle \sum _{n=0}^{\infty }{C}_n\sinh \left(\frac{(2n+1)\pi }{2a}b\right){\displaystyle \underset{0}{\overset{a}{\int }}\left\{\sin \left(\frac{(2n+1)\pi }{2a}x\right)\sin \left(\frac{(2m+1)\pi }{2a}x\right)\right\}dx}}\\ {\displaystyle \underset{0}{\overset{a}{\int }}V(x,b)\sin \left(\frac{(2n+1)\pi }{2a}x\right)dx}=\frac{a}{2}{C}_n\sinh \left(\frac{(2n+1)\pi }{2a}b\right)\end{array}}$

El potencial V(x,y) en cualquier punto (x,y) de la región rectangular es

${\displaystyle V(x,y)={\displaystyle \sum _{n=0}^{\infty }\left(C_n\sinh \left(\frac{(2n+1)\pi }{2a}y\right)\right)\sin \left(\frac{(2n+1)\pi }{2a}x\right)}}$

Ejemplo

Sea V(x,b)=x. Para calcular el coeficiente C_n integramos por partes

${\displaystyle \begin{array}{l}\{\begin{array}{l}u=x,du=dx\\ dv=\sin \left(\frac{(2n+1)\pi }{2a}x\right)dx,v=-\frac{2a}{(2n+1)\pi }\cos \left(\frac{(2n+1)\pi }{2a}x\right)\end{array}\\ {\displaystyle \int x\sin \left(\frac{(2n+1)\pi }{2a}x\right)dx}=-x\frac{2a}{(2n+1)\pi }\cos \left(\frac{(2n+1)\pi }{2a}x\right)+{\left(\frac{2a}{(2n+1)\pi }\right)}^2\sin \left(\frac{(2n+1)\pi }{2a}x\right)\\ {\displaystyle \underset{0}{\overset{a}{\int }}x\sin \left(\frac{(2n+1)\pi }{2a}x\right)dx}={\left(-1\right)}^n{\left(\frac{2a}{(2n+1)\pi }\right)}^2\end{array}}$

El resultado es

${\displaystyle C_n={\left(-1\right)}^n\frac{8a}{{\left(2n+1\right)}^2{\pi }^2\sinh \left(\frac{(2n+1)\pi }{2a}b\right)}}$

Sea

• a=2
• b=1

Definimos la función que calcula el potencial V(x,y), empleando N=100 términos del desarrollo en serie

function z = laplace_potencial_2(x,y, N, a, b)
    z=0;
    for n=0:N
        C=8*a*(-1)^n/(((2*n+1)*pi)^2*sinh((2*n+1)*pi*b/(2*a)));
        z=z+C*sinh((2*n+1)*pi*y/(2*a)).*sin((2*n+1)*pi*x/(2*a));
    end
end

Representamos las líneas equipotenciales mediante fcontour

a=2; %dimensiones
b=1;
N=100;
f=@(x,y) laplace_potencial_2(x,y, N, a, b);
fcontour(f,[0,a,0,b], 'fill','on')
colorbar
xlabel('x')
ylabel('y')
title('V(x,y)')

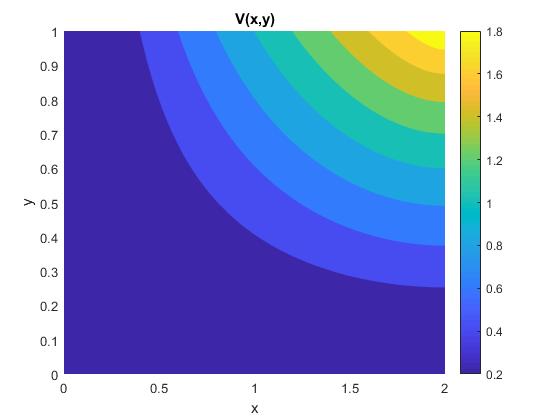
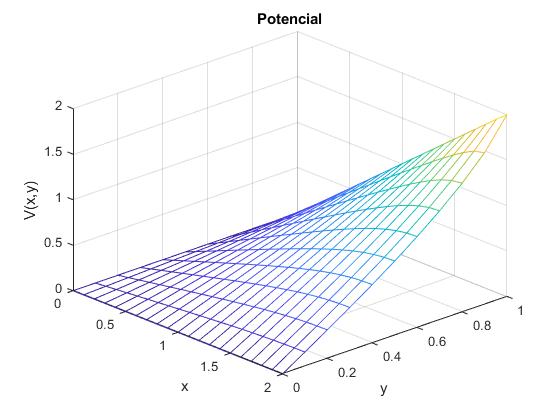
Representamos la función V(x,y) mediante mesh

a=2; %dimensiones
b=1;
[x,y] = meshgrid(0:0.1:a, 0:0.1:b);
N=100;
z=laplace_potencial_2(x,y, N, a, b);
mesh(x,y,z)
xlabel('x')
ylabel('y')
zlabel('V(x,y)')
title('Potencial')
view(47,32)

Aplicaremos el principio de superposición para resolver la ecuación de Laplace en un recinto rectangular con otras condiciones de contorno en cada uno de sus lados

Referencias

Larry Caretto, Solution of Laplace's Equation. College of Engineering and Computer Science. Mechanical Engineering Department. California State University. http://www.csun.edu/~lcaretto/me501b/laplace.doc. February 6, 2009