Placas conductoras perpendiculares

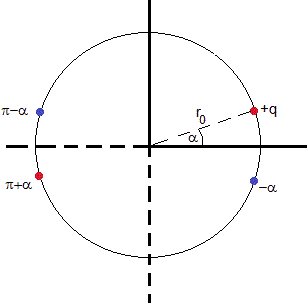
Consideremos dos placas conductoras planas e indefinidas conectadas a tierra, que se cruzan a lo largo del eje Z formando un ángulo de 90°. En la figura, se representa el corte en el plano z=0, es decir, el plano XY

Recordamos que el sistema formado por una carga y un conductor plano e indefinido conectado a tierra es equivalente a dos cargas una real y otra denominada imagen, iguales y opuestas

Situamos una carga +q en el punto de coordenadas polares (r₀, α).

• La carga imagen de +q (r₀, α) producida por el plano horizontal y=0 es -q (r₀, -α), en color azul
• La carga imagen de +q (r₀, α) producida por el plano vertical x=0 es -q (r₀, π-α), en color azul
• La carga imagen de -q (r₀, π-α) producida por el plano y=0 es +q (r₀, π+α), en color rojo

Como vemos en la figura, se ha dibujado la carga +q, sus cargas imagen y las imágenes de las imágenes.

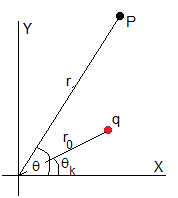
El potencial producido en el punto P (r, θ, z) por una carga +q situada en el punto (r₀, θ_k) es

${\displaystyle V_k=\frac{1}{4\pi {\epsilon }_0}\frac{q}{\sqrt{r^2+r_0^2+z^2-2r{r}_0\cos \left(\theta -{\theta }_k\right)}}}$

El potencial total creado en P por el sistema de cuatro cargas al que equivale el sistema formado por una carga positiva +q entre dos planos conductores conectados a tierra y que intersecan formando un ángulo de 90°, es

${\displaystyle \begin{array}{l}V=\frac{1}{4\pi {\epsilon }_0}\frac{q}{\sqrt{r^2+r_0^2+z^2-2r{r}_0\cos \left(\theta -\alpha \right)}}+\frac{1}{4\pi {\epsilon }_0}\frac{-q}{\sqrt{r^2+r_0^2+z^2-2r{r}_0\cos \left(\theta +\alpha \right)}}\\ +\frac{1}{4\pi {\epsilon }_0}\frac{-q}{\sqrt{r^2+r_0^2+z^2-2r{r}_0\cos \left(\theta -\pi +\alpha \right)}}+\frac{1}{4\pi {\epsilon }_0}\frac{q}{\sqrt{r^2+r_0^2+z^2-2r{r}_0\cos \left(\theta -\pi -\alpha \right)}}\end{array}}$

o bien

${\displaystyle \begin{array}{l}V=\frac{1}{4\pi {\epsilon }_0}\frac{q}{\sqrt{r^2+r_0^2+z^2-2r{r}_0\cos \left(\theta -\alpha \right)}}-\frac{1}{4\pi {\epsilon }_0}\frac{q}{\sqrt{r^2+r_0^2+z^2-2r{r}_0\cos \left(\theta +\alpha \right)}}\\ -\frac{1}{4\pi {\epsilon }_0}\frac{q}{\sqrt{r^2+r_0^2+z^2+2r{r}_0\cos \left(\theta +\alpha \right)}}+\frac{1}{4\pi {\epsilon }_0}\frac{q}{\sqrt{r^2+r_0^2+z^2+2r{r}_0\cos \left(\theta -\alpha \right)}}\end{array}}$

Conocido el potencial, calculamos el campo eléctrico

${\displaystyle \overrightarrow{E}=-\frac{\partial V}{\partial r}\widehat{r}-\frac{1}{r}\frac{\partial V}{\partial \theta }\widehat{\theta }-\frac{\partial V}{\partial z}\widehat{z}}$

La primera es la componente a lo largo de la dirección radial, la última es la componente a lo largo del eje Z de intersección de los planos. Tenemos interés en la componente del campo perpendicular a los planos, E_θ

${\displaystyle \begin{array}{l}{E}_{\theta }=\frac{q}{4\pi {\epsilon }_0}\frac{r_0\sin \left(\theta -\alpha \right)}{{\left(r^2+r_0^2+z^2-2r{r}_0\cos \left(\theta -\alpha \right)\right)}^{3/2}}-\frac{q}{4\pi {\epsilon }_0}\frac{r_0\sin \left(\theta +\alpha \right)}{{\left(r^2+r_0^2+z^2-2r{r}_0\cos \left(\theta +\alpha \right)\right)}^{3/2}}\\ +\frac{q}{4\pi {\epsilon }_0}\frac{r_0\sin \left(\theta +\alpha \right)}{{\left(r^2+r_0^2+z^2+2r{r}_0\cos \left(\theta +\alpha \right)\right)}^{3/2}}-\frac{q}{4\pi {\epsilon }_0}\frac{r_0\sin \left(\theta -\alpha \right)}{{\left(r^2+r_0^2+z^2+2r{r}_0\cos \left(\theta -\alpha \right)\right)}^{3/2}}\end{array}}$

Carga en el plano horizontal

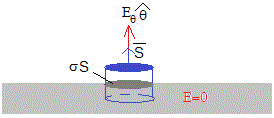
En la figura se representa el plano conductor horizontal. El campo eléctrico en el interior del conductor es cero, E=0. El campo eléctrico en las proximidades de un conductor es perpendicular a su superficie y viene dado por la componente E_θ para θ=0), que denominaremos E₀

Tomamos una superficie cilíndrica cuyas bases tiene área S. Como en el interior del conductor el campo es cero, no hay flujo por la base inferior del cilindro, por la superficie lateral tampoco hay flujo. El flujo del campo eléctrico se produce a través de la base superior de la superficie cilíndrica

${\displaystyle \overrightarrow{E}·\overrightarrow{S}=E_{0}S·\cos 0=E_{0}S}$

Sabiendo que la carga en el interior de la superficie cilíndrica es σS, aplicamos la ley de Gauss

${\displaystyle E_{0}S=\frac{\sigma S}{{\epsilon }_0}\sigma ={\epsilon }_0{E}_0}$

La densidad de carga en el plano horizontal es

${\displaystyle {\sigma }_f\left(\theta =0\right)=-\frac{2q}{4\pi }\frac{r_0\sin \alpha }{{\left(r^2+r_0^2+z^2-2r{r}_0\cos \alpha \right)}^{3/2}}+\frac{2q}{4\pi }\frac{r_0\sin \alpha }{{\left(r^2+r_0^2+z^2+2r{r}_0\cos \alpha \right)}^{3/2}}}$

Carga total en cada placa conductora horizontal es

${\displaystyle q\left(\theta =0\right)={\displaystyle \underset{r=0}{\overset{\infty }{\int }}{\displaystyle \underset{z=-\infty }{\overset{z=+\infty }{\int }}{\sigma }_f\left(\theta =0\right)dr·dz}}}$

Tenemos que calcular las integrales dobles

${\displaystyle q\left(\theta =0\right)=-\frac{q}{2\pi }{r}_0\sin \alpha \left\{\begin{array}{l}{\displaystyle \underset{0}{\overset{{}^{\infty }}{\int }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\frac{dr·dz}{{\left(r^2+r_0^2+z^2-2r{r}_0\cos \alpha \right)}^{3/2}}}}\\ -{\displaystyle \underset{0}{\overset{{}^{\infty }}{\int }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\frac{dr·dz}{{\left(r^2+r_0^2+z^2+2r{r}_0\cos \alpha \right)}^{3/2}}}}\end{array}\right\}}$

Primero integramos respecto a z una función de la forma

${\displaystyle {\displaystyle \underset{z=-\infty }{\overset{z=\infty }{\int }}\frac{dz}{{\left(a^2+z^2\right)}^{3/2}}}}$

Se hace un cambio de variable y se integra

${\displaystyle \begin{array}{l}z=a\tan xdz=\frac{a}{{\cos }^{2}x}dx\\ {\displaystyle \int \frac{dz}{{\left(a^2+z^2\right)}^{3/2}}=}\frac{1}{a^2}{\displaystyle \int \cos x·dx=\frac{1}{a^2}\sin x=}\frac{1}{a^2}\frac{z}{\sqrt{a^2+z^2}}\\ {\displaystyle \underset{z=-\infty }{\overset{z=\infty }{\int }}\frac{dz}{{\left(a^2+z^2\right)}^{3/2}}}=\frac{2}{a^2}\\ a^2=r^2+r_0^2\pm 2r{r}_0\cos \alpha \end{array}}$

La expresión de la carga en el plano horizontal se ha reducido a

${\displaystyle q\left(\theta =0\right)=-\frac{q}{\pi }{r}_0\sin \alpha \left\{{\displaystyle \underset{0}{\overset{{}^{\infty }}{\int }}\frac{dr}{r^2+r_0^2-2r{r}_0\cos \alpha }-{\displaystyle \underset{0}{\overset{{}^{\infty }}{\int }}\frac{dr}{r^2+r_0^2+2r{r}_0\cos \alpha }}}\right\}}$

Integramos una función de la forma

${\displaystyle {\displaystyle \int \frac{dx}{x^2+bx+c}}={\displaystyle \int \frac{dx}{{\left(x+\frac{b}{2}\right)}^2+\left(c-\frac{b^2}{4}\right)}=\frac{1}{\sqrt{c-\frac{b^2}{4}}}{\displaystyle \int \frac{du}{u^2+1}}}}$

Haciendo el cambio u=tant, du=dt/cos²t, la integral es inmediata

${\displaystyle \begin{array}{l}\frac{1}{\sqrt{c-\frac{b^2}{4}}}{\displaystyle \int dt}=\frac{1}{\sqrt{c-\frac{b^2}{4}}}{\tan }^{-1}\left(\frac{x+\frac{b}{2}}{\sqrt{c-\frac{b^2}{4}}}\right)=\frac{1}{r_0\sin \alpha }{\tan }^{-1}\left(\frac{r}{r_0\sin \alpha }\pm \cot \alpha \right)\\ b=\pm 2r_0\cos \alpha c=r_0^2\end{array}}$

El resultado final es

${\displaystyle \begin{array}{l}q\left(\theta =0\right)=-\frac{q}{\pi }\left\{\left(\frac{\pi }{2}-\frac{\pi }{2}\right)-\left({\tan }^{-1}\left(-\cot \alpha \right)-{\tan }^{-1}\left(\cot \alpha \right)\right)\right\}=\\ -\frac{q}{\pi }\left\{-\left(-\left(\frac{\pi }{2}-\alpha \right)-\left(\frac{\pi }{2}-\alpha \right)\right)\right\}=-\frac{q}{\pi }\left(\pi -2\alpha \right)\end{array}}$

Carga en el plano vertical

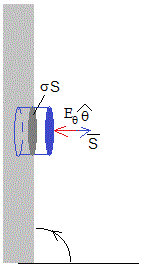
En la figura se representa el plano conductor horizontal. El campo eléctrico en el interior del conductor es cero, E=0. El campo eléctrico en las proximidades de un conductor es perpendicular a su superficie y viene dado por la componente E_θ para θ=π/2, que denominaremos E_π/2, dirigido hacia la placa

Tomamos una superficie cilíndrica cuyas bases tiene área S. Como en el interior del conductor el campo es cero, no hay flujo por la base izquierda del cilindro, por la superficie lateral tampoco hay flujo. El flujo del campo eléctrico se produce a través de la base derecha de la superficie cilíndrica

${\displaystyle \overrightarrow{E}·\overrightarrow{S}=E_{\pi /2}S·\cos 180º=-E_{\pi /2}S}$

Sabiendo que la carga en el interior de la superficie cilíndrica es σS, aplicamos la ley de Gauss

${\displaystyle -E_{\pi /2}S=\frac{\sigma S}{{\epsilon }_0}\sigma =-{\epsilon }_0{E}_{\pi /2}}$

La densidad de carga es

${\displaystyle {\sigma }_f\left(\theta =\frac{\pi }{2}\right)=-\frac{q}{2\pi }\frac{r_0\cos \alpha }{{\left(r^2+r_0^2+z^2-2r{r}_0\sin \alpha \right)}^{3/2}}+\frac{q}{2\pi }\frac{r_0\cos \alpha }{{\left(r^2+r_0^2+z^2+2r{r}_0\sin \alpha \right)}^{3/2}}}$

Integramos para obtener la carga en la placa conductora vertical

${\displaystyle q\left(\theta =\frac{\pi }{2}\right)={\displaystyle \underset{r=0}{\overset{\infty }{\int }}{\displaystyle \underset{z=-\infty }{\overset{z=+\infty }{\int }}{\sigma }_f\left(\theta =\frac{\pi }{2}\right)dr·dz}}}$

El procedimiento de integración lo hemos descrito en el apartado anterior, el resultado es

${\displaystyle \begin{array}{l}q\left(\theta =\frac{\pi }{2}\right)=-\frac{q}{2\pi }{r}_0\cos \alpha \left\{\begin{array}{l}{\displaystyle \underset{0}{\overset{{}^{\infty }}{\int }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\frac{dr·dz}{{\left(r^2+r_0^2+z^2-2r{r}_0\sin \alpha \right)}^{3/2}}}}-\\ {\displaystyle \underset{0}{\overset{{}^{\infty }}{\int }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\frac{dr·dz}{{\left(r^2+r_0^2+z^2+2r{r}_0\sin \alpha \right)}^{3/2}}}}\end{array}\right\}=\\ -\frac{q}{\pi }{r}_0\cos \alpha \left\{{\displaystyle \underset{0}{\overset{{}^{\infty }}{\int }}\frac{dr}{r^2+r_0^2-2r{r}_0\sin \alpha }-{\displaystyle \underset{0}{\overset{{}^{\infty }}{\int }}\frac{dr}{r^2+r_0^2+2r{r}_0\sin \alpha }}}\right\}=\\ -\frac{q}{\pi }{\left\{{\tan }^{-1}\left(\frac{r}{r_0\cos \alpha }-\tan \alpha \right)-{\tan }^{-1}\left(\frac{r}{r_0\cos \alpha }+\tan \alpha \right)\right\}}_0^{\infty }=\\ -\frac{q}{\pi }\left\{\left(\frac{\pi }{2}-\frac{\pi }{2}\right)-\left({\tan }^{-1}\left(-\tan \alpha \right)-{\tan }^{-1}\left(\tan \alpha \right)\right)\right\}=\\ -\frac{q}{\pi }\left\{-\left(-\alpha -\alpha \right)\right\}=-2\frac{q}{\pi }\alpha \end{array}}$

La suma de las cargas en el plano horizontal y en el plano vertical valen

${\displaystyle q\left(\theta =0\right)+q\left(\theta =\frac{\pi }{2}\right)=-\frac{q}{\pi }\left(\pi -2\alpha \right)-2\frac{q}{\pi }\alpha =-q}$

Los planos conductores forman un ángulo π/n

Una vez que hemos estudiado el caso de una carga positiva entre dos planos conductores conectados a tierra que forman un ángulo de 90°, consideremos el caso más general, suponiendo que los planos conductores forman un ángulo π/n, donde n es un número entero. Por ejemplo, n=2, corresponde a planos perpendiculares

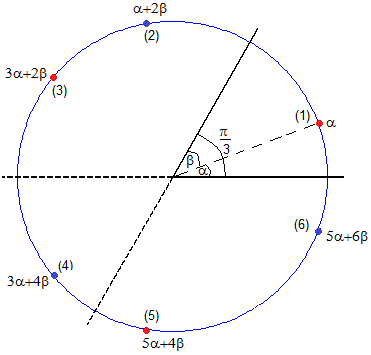
Consideremos que n=3, se sitúa una carga +q entre dos planos indefinidos conductores que forman un ángulo de π/3 rad ó 60°. La carga +q está a una distancia r₀ del eje (recta de intersección de los dos planos) y forma un ángulo α=20° con el plano horizontal y un ángulo β=90-α=40° con el plano inclinado, tal como se muestra en la figura.

Creamos un script para mostrar las cargas imágenes de +q y las imágenes de las imágenes y sus posiciones angulares en un circunferencia de radio r₀.

${\displaystyle {\theta }_k=\{\begin{array}{l}(k-1)\beta +k\alpha k\text{impar}\\ k\beta +(k-1)\alpha k\text{par}\end{array}}$

Donde el índice k va de 1 a 2n

ang=0:pi/180:2*pi;
n=3;
alfa=20*pi/180;
beta=pi/n-alfa;
hold on
plot(cos(ang),sin(ang))
line([0,1.1],[0,0],'lineWidth',1.5, 'color','k')
line([0,-1.1],[0,0],'lineWidth',1.5, 'color','k','lineStyle','--')
line([0,1.1*cos(pi/n)],[0,1.1*sin(pi/n)],'lineWidth',1.5, 'color','k')
line([0,-1.1*cos(pi/n)],[0,-1.1*sin(pi/n)],'lineWidth',1.5, 'color',
'k','lineStyle','--')
 
for k=1:2:2*n
    th=(k-1)*beta+k*alfa;
    plot(cos(th),sin(th),'o','markersize',6,'markeredgecolor','r',
'markerfacecolor','r')
   th=(k+1)*beta+(k+1-1)*alfa;
    plot(cos(th),sin(th),'o','markersize',6,'markeredgecolor','b',
'markerfacecolor','b')
end 
 
hold off
axis equal
ylim([-1.1,1.1])

El potencial producido en un punto P (r, θ, z), por el sistema de cargas positivas (rojas) y negativas (azules) es

${\displaystyle V=-\frac{q}{4\pi {\epsilon }_0}{\displaystyle \sum _{k=1}^{2n}\frac{{\left(-1\right)}^k}{\sqrt{r^2+r_0^2+z^2-2r{r}_0\cos \left(\theta -{\theta }_k\right)}}}}$

Para k=1, la carga es positiva, para k=2 la carga es negativa y así, sucesivamente

Calculamos la componente E_θ del campo

${\displaystyle E_{\theta }=-\frac{1}{r}\frac{\partial V}{\partial \theta }=-\frac{q}{4\pi {\epsilon }_0}{\displaystyle \sum _{k=1}^{2n}\frac{{\left(-1\right)}^k{r}_0\sin \left(\theta -{\theta }_k\right)}{{\left(r^2+r_0^2+z^2-2r{r}_0\cos \left(\theta -{\theta }_k\right)\right)}^{3/2}}}}$

Carga en el plano horizontal

La densidad de carga, aplicando la ley de Gauss en el plano conductor horizontal es

${\displaystyle {\sigma }_f\left(\theta =0\right)={\epsilon }_0{E}_{\theta }\left(\theta =0\right)=\frac{q}{4\pi }{\displaystyle \sum _{k=1}^{2n}\frac{{\left(-1\right)}^k{r}_0\sin {\theta }_k}{{\left(r^2+r_0^2+z^2-2r{r}_0\cos {\theta }_k\right)}^{3/2}}}}$

Comprobación: si ponemos n=2, β=π/2-α, sabiendo que las posiciones angulares de las cargas son: θ₁=α, θ₂=π-α, θ₃=π+α, θ₄=-α, obtenemos la misma expresión para la densidad de carga en el plano horizontal θ=0, que en el apartado anterior

Integramos para obtener la carga en dicho plano conductor

${\displaystyle \begin{array}{l}q\left(\theta =0\right)={\displaystyle \underset{r=0}{\overset{\infty }{\int }}{\displaystyle \underset{z=-\infty }{\overset{z=+\infty }{\int }}{\sigma }_f\left(\theta =0\right)dr·dz}}=\\ \frac{q}{4\pi }{\displaystyle \sum _{k=1}^{2n}{\left(-1\right)}^k{r}_0\sin {\theta }_k{\displaystyle \underset{r=0}{\overset{\infty }{\int }}{\displaystyle \underset{z=-\infty }{\overset{z=+\infty }{\int }}\frac{dr·dz}{{\left(r^2+r_0^2+z^2-2r{r}_0\cos {\theta }_k\right)}^{3/2}}}}}=\\ {\frac{q}{2\pi }{\displaystyle \sum _{k=1}^{2n}{\left(-1\right)}^k{\tan }^{-1}\left(\frac{r}{r_0\sin {\theta }_k}-\cot {\theta }_k\right)}|}_0^{\infty }=\\ \frac{q}{2\pi }{\displaystyle \sum _{k=1}^{2n}{\left(-1\right)}^k\left\{{\tan }^{-1}{\left(\frac{r}{r_0\sin {\theta }_k}\right)}_{r=\infty }+{\tan }^{-1}\left(\cot {\theta }_k\right)\right\}}\end{array}}$

Utilizamos MATLAB para obtener el resultado de la suma y para comprobar que es múltiplo del ángulo β, teniendo en cuenta que

${\displaystyle {\tan }^{-1}{\left(\frac{r}{r_0\sin {\theta }_k}\right)}_{r=\infty }=\{\begin{array}{l}\pi /20<{\theta }_k<\pi \\ -\pi /2\pi <{\theta }_k<2\pi \end{array}}$

n=3;
alfa=20*pi/180;
beta=pi/n-alfa;
suma=0;
for k=1:2:2*n
    th=(k-1)*beta+k*alfa;
    suma=suma+(-1)^k*(sign(sin(th))*pi/2+atan(1/tan(th)));
   th=(k+1)*beta+(k+1-1)*alfa;
   suma=suma+(-1)^(k+1)*(sign(sin(th))*pi/2+atan(1/tan(th)));
end 
disp(suma/beta)

-6.0000

El resultado de la suma es -2nβ. Se puede comprobar variando el ángulo β, o n

La carga en la placa conductora horizontal es

${\displaystyle q\left(\theta =0\right)=\frac{q}{2\pi }\left(-2n\beta \right)=-\frac{q}{\pi }n\beta }$

El mismo resultado que hemos obtenido anteriormente, con n=2 y β=π/2-α

Carga en el plano inclinado

La densidad de carga en el plano inclinado π/n es

${\displaystyle {\sigma }_f\left(\theta =\frac{\pi }{n}\right)=-{\epsilon }_0{E}_{\theta }\left(\theta =\frac{\pi }{n}\right)=\frac{q}{4\pi }{\displaystyle \sum _{k=1}^{2n}\frac{{\left(-1\right)}^k{r}_0\sin \left(\frac{\pi }{n}-{\theta }_k\right)}{{\left(r^2+r_0^2+z^2-2r{r}_0\cos \left(\frac{\pi }{n}-{\theta }_k\right)\right)}^{3/2}}}}$

Comprobación: si ponemos n=2, β=π/2-α, sabiendo que las posiciones angulares de las cargas son: θ₁=α, θ₂=π-α, θ₃=π+α, θ₄=-α, obtenemos la misma expresión para la densidad de carga en el plano vertical θ=π/2 que en el apartado anterior

Integramos para obtener la carga en dicho plano

${\displaystyle \begin{array}{l}q\left(\theta =\frac{\pi }{n}\right)={\displaystyle \underset{r=0}{\overset{\infty }{\int }}{\displaystyle \underset{z=-\infty }{\overset{z=+\infty }{\int }}{\sigma }_f\left(\theta =\frac{\pi }{n}\right)dr·dz}}=\\ \frac{q}{4\pi }{\displaystyle \sum _{k=1}^{2n}{\left(-1\right)}^k{r}_0\sin \left(\frac{\pi }{n}-{\theta }_k\right){\displaystyle \underset{r=0}{\overset{\infty }{\int }}{\displaystyle \underset{z=-\infty }{\overset{z=+\infty }{\int }}\frac{dr·dz}{{\left(r^2+r_0^2+z^2-2r{r}_0\cos \left(\frac{\pi }{n}-{\theta }_k\right)\right)}^{3/2}}}}}=\\ {\frac{q}{2\pi }{\displaystyle \sum _{k=1}^{2n}{\left(-1\right)}^k{\tan }^{-1}\left(\frac{r}{r_0\sin \left(\frac{\pi }{n}-{\theta }_k\right)}-\cot \left(\frac{\pi }{n}-{\theta }_k\right)\right)}|}_0^{\infty }=\\ \frac{q}{2\pi }{\displaystyle \sum _{k=1}^{2n}{\left(-1\right)}^k\left\{{\tan }^{-1}{\left(\frac{r}{r_0\sin \left(\frac{\pi }{n}-{\theta }_k\right)}\right)}_{r=\infty }+{\tan }^{-1}\left(\cot \left(\frac{\pi }{n}-{\theta }_k\right)\right)\right\}}\end{array}}$

Utilizamos MATLAB para obtener el resultado de la suma y comprobar que es un múltiplo del ángulo α

n=3;
alfa=20*pi/180;
beta=pi/n-alfa;
suma=0;
for k=1:2:2*n
    th=(k-1)*beta+k*alfa;
    suma=suma+(-1)^k*(sign(sin(pi/n-th))*pi/2+atan(1/tan(pi/n-th)));
   th=(k+1)*beta+(k+1-1)*alfa;
   suma=suma+(-1)^(k+1)*(sign(sin(pi/n-th))*pi/2+atan(1/tan(pi/n-th)));
end 
disp(suma/alfa)

-6.0000

El resultado de la suma es -2nα. La carga en la placa conductora inclinada es

${\displaystyle q\left(\theta =\frac{\pi }{n}\right)=\frac{q}{2\pi }\left(-2n\alpha \right)=-\frac{q}{\pi }n\alpha }$

La suma de las cargas en ambas placas conductoras es

${\displaystyle q\left(\theta =0\right)+q\left(\theta =\frac{\pi }{n}\right)=-\frac{q}{\pi }n\beta -\frac{q}{\pi }n\alpha =-\frac{q}{\pi }n(\alpha +\beta )=\frac{q}{\pi }n\frac{\pi }{n}=-q}$

Referencias

Markus Zahn. Point charge between two paralell grounded planes. Am. J. Phys. Vol. 44, No. 11, November 1976, pp. 1132-1134