Esfera cargada próxima a un plano conductor a potencial cero
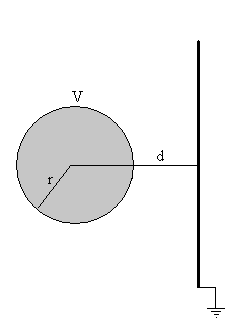
Consideremos una esfera cargada próxima a un plano conductor a potencial cero, tal como se aprecia en la figura
Sustituiremos la esfera y el plano por una sucesión de cargas puntuales de signos contrarios que converge a cero rápidamente y que hacen que las dos superficies (esfera y plano) sean equipotenciales.
Supongamos que la esfera de radio r, está a un potencial V y su centro dista d>r del plano a potencial cero.
Los pasos para aplicar el método de las imágenes son los siguientes:
-
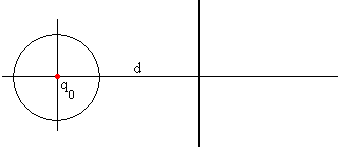
Colocamos una carga q0 en el centro de la esfera. Esto hace que la superficie esférica de radio r esté a un potencial V.
-
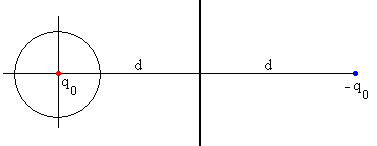
Colocamos una carga –q0 a una distancia 2d del centro de la esfera. Esto hace que el plano sea una superficie equipotencial, pero ya no lo es la esfera.
-
Colocamos una carga q1 en el interior de la esfera. Calculamos el valor de q1 y su posición x1 para que la esfera sea una superficie equipotencial, aunque deje de serlo el plano
-
Colocamos una carga –q1 simétrica a q1 para el plano sea equipotencial, pero deja de serlo la superficie esférica
-
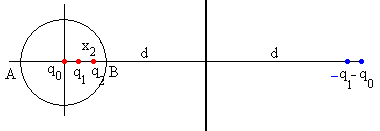
Colocamos una carga q2 en el interior de la esfera, para que esta sea equipotencial, aunque el plano deje de serlo
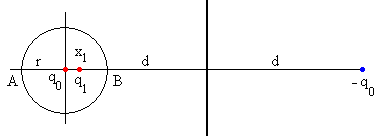
El potencial en A (-r, 0) debido a las cargas –q0 y q1 lo hacemos cero
El potencial en B (r, 0) debido a las cargas –q0 y q1 lo hacemos cero
Despejamos q1 y x1 de este sistema de dos ecuaciones con dos incógnitas
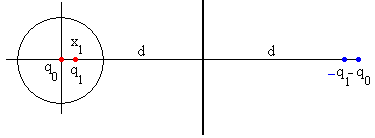
El potencial en A (-r, 0) debido a las cargas –q1 y q2 lo hacemos cero
El potencial en B (r, 0) debido a las cargas –q1 y q2 lo hacemos cero
Despejamos q2 y x2 en este sistema de dos ecuaciones con dos incógnitas
Continuamos el proceso que converge rápidamente hasta que tenemos la precisión deseada
Relaciones recursivas
Calculamos la sucesión de cargas qi y sus posiciones xi mediante las relaciones recursivas
Ejemplo:
Tomamos d=3r, q0=1 y r=1
d=3;
r=1;
x=0;
q=1;
i=0;
disp('Paso, posición, carga')
fprintf('%i, %1.8f, %1.8f\n',i,x,q)
format long;
for i=1:5
x=r^2/(2*d-x);
q=q*r/(2*d-x);
fprintf('%i, %1.8f, %1.8f\n',i,x,q)
end
Paso, posición, carga 0, 0.00000000, 1.00000000 1, 0.16666667, 0.17142857 2, 0.17142857, 0.02941176 3, 0.17156863, 0.00504626 4, 0.17157275, 0.00086580 5, 0.17157287, 0.00014855
| Paso | Posición xi | Carga qi |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0.166667 | 0.16667 |
| 2 | 0.171429 | 0.02857 |
| 3 | 0.171569 | 0.00490 |
| 4 | 0.171573 | 0.00084 |
| 5 | 0.171573 | 0.00014 |
Sustituímos la distribución de carga formada por una esfera de radio r y un plano a potencial cero situado a una distancia d>r del centro de la esfera, por una sucesión de cargas puntuales positivas situadas en la esfera y sus correspondientes cargas negativas situadas simétricamente respecto del plano. Esta sucesión tiende a cero rápidamente.
Así la carga qi está en la posición xi y su simétrica –qi está en la posición 2d-xi
La carga total de la esfera es
Solamente q0 contribuye al potencial de la esfera, las cargas q1, q2, ... anulan el potencial de la esfera y lo mismo ocurre con todos los restantes pares de cargas. El potencial de la esfera es, por tanto, V=q0/(4πє0r)
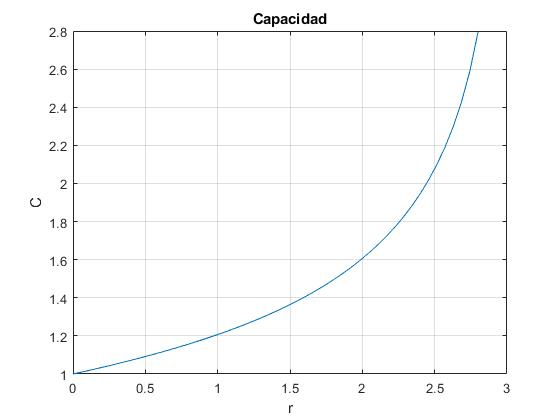
La capacidad
Representamos
en función de r<d
d=3;
q0=1;
rr=linspace(0,2.8,50);
j=1;
C=zeros(1,length(rr));
for r=rr
x=0;
q=q0;
Q=q;
for i=1:50
x=r^2/(2*d-x);
q=q*r/(2*d-x);
Q=Q+q;
end
C(j)=Q/q0;
j=j+1;
end
plot(rr,C)
xlabel('r')
ylabel('C')
grid on
title('Capacidad')
Líneas de campo y equipotenciales
Calculamos el campo y el potencial producido en el punto P (x, y) por el par de cargas qi situada en el punto xi y su simétrica –qi en la posición 2d-xi
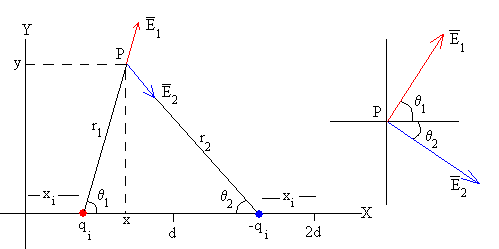
El módulo del campo E1 producido por la carga qi es
El módulo del campo E2 producido por la carga simétrica -qi es
Las componentes del campo son
Eix=E1·cosθ1+E2·cosθ2
Eiy=E1·sinθ1-E2·sinθ2
El potencial Vi en el punto P debido a las dos cargas es
El campo y el potencial total es la suma de todos los campos y potenciales producidos por los pares de cargas dispuestas simétricamente al plano
Actividades
Se introduce
-
La distancia d entre el centro de la esfera cargada y el plano a potencial cero en unidades del radio r de la esfera, en el control titulado Distancia
Se pulsa el botón titulado Nuevo
Se trazan las líneas de campo (en color blanco) y las superficies equipotenciales (en color azul claro).
Las superficies equipotenciales se han trazado, en intervalos de 0.05 unidades arbitrarias, tomando el potencial de la esfera como la unidad.
Referencias
Lorrain P. Corson D. Campos y ondas electromagnéticas. Selecciones Científicas (1972), págs. 159-162

