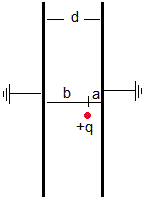
Cuando situamos una carga puntual q entre dos conductores planos paralelos separados una distancia d y conectados a tierra se producen infinitas cargas imagen, del mismo modo que un objeto situado entre dos espejos planos paralelos

Consideremos una carga puntual q situada a una distancia a del plano derecho y a una distancia b del plano izquierdo, siendo d=a+b la separación entre los dos planos paralelos conectados a Tierra

Situamos el origen del eje X en la carga real +q y calcularemos las distancias de las cargas imágenes a la carga real +q a uno y otro lado de dicha carga, en dos etapas:

1. La carga real +q (roja) se refleja en el plano izquierdo, dibujamos la carga imagen especular negativa -q (azul) y calculamos su distancia a la carga real. Esta carga imagen se refleja en el plano derecho, dibujamos la carga imagen +q (roja) y calculamos su distancia a la carga real y así, sucesivamente

2. La carga origen +q (roja) se refleja en el plano derecho, dibujamos la carga imagen especular negativa -q (azul) y calculamos su distancia a la carga real. Esta carga imagen se refleja en el plano izquierdo, dibujamos la carga imagen +q (roja) y calculamos su distancia a la carga origen y así, sucesivamente

La primera etapa, se muestra a la izquierda de la figura y la segunda, a la derecha

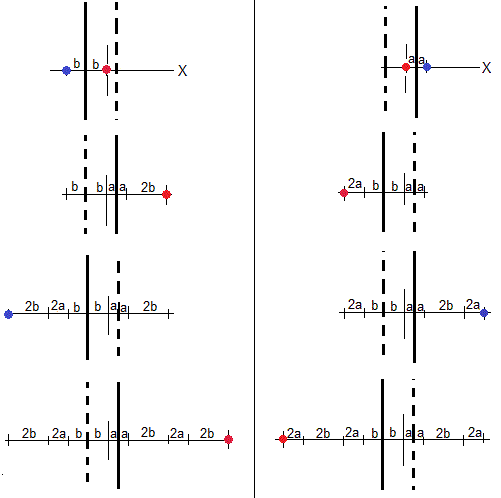
• Plano izquierdo

En la primera figura, la carga puntual +q (roja) se refleja en el plano conductor izquierdo a potencial cero, produciendo la carga imagen -q (azul) situada en -2b a la izquierda de la carga real.

En la segunda figura, dicha carga puntual -q se refleja en el plano conductor derecho a potencial cero, produciendo la carga imagen +q situada en (2a+2b) a la derecha de la carga real

En la tercera figura, dicha carga puntual +q se refleja en el plano conductor izquierdo, produciendo la carga imagen -q situada en -(2a+4b)

En la cuarta figura, dicha carga puntual -q se refleja en el plano conductor derecho, produciendo la carga imagen +q situada en (4a+4b)

y así, sucesivamente

• Plano derecho

En la primera figura, la carga puntual +q (roja) se refleja en el plano conductor derecho, produciendo la carga imagen -q (azul) situada en 2a

En la segunda figura, dicha carga puntual -q se refleja en el plano conductor izquierdo, produciendo la carga imagen +q (azul) situada en -(2a+2b)

En la tercera figura, dicha carga puntual +q se refleja en el plano conductor derecho, produciendo la carga imagen -q situada en (4a+2b)

En la cuarta figura, dicha carga puntual -q se refleja en el plano conductor izquierdo, produciendo la carga imagen +q situada en -(4a+4b)

y así, sucesivamente

Las distancias de las cargas imágenes de la carga real +q, situada entre dos planos conductores a potencial cero, son las siguientes:

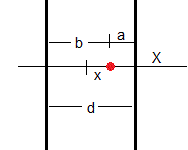
Llamamos a=d/2-x y b=d/2+x. Las distancias de las cargas imágenes de +q, a la carga origen expresados en términos de x, son las siguientes:

d=1; %distancia entre placas
n=3; %12 cargas imagen (6+ y 6-) a ambos lados
x=0.25; %posición de la carga real +q
%el origen en el punto medio entre placas
xPos=(-2*n:2:2*n)*d+x*ones(1,2*n+1);
xPos(n+1)=[]; %elimina el elemento central
xNeg=[-((2*(1:n)-ones(1,n))*d+2*x*ones(1,n)), ((2*(1:n)-ones(1,n))*d
-2*x*ones(1,n))]+x*ones(1,2*n); 

hold on
%cargas imagen
plot(xPos,0,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
plot(xNeg,0,'o','markersize',3,'markeredgecolor','b','markerfacecolor','b')
%placas conductoras a potencial cero
line([-d/2,-d/2],[-1,1],'lineWidth',1.5,'color','k')
line([d/2,d/2],[-1,1],'lineWidth',1.5,'color','k')
%carga real
plot(x,0,'o','markersize',5,'markeredgecolor','r','markerfacecolor','r')
hold off
set(gca,'ytick',[])
grid on
xlabel('x')
title('Cargas imagen')

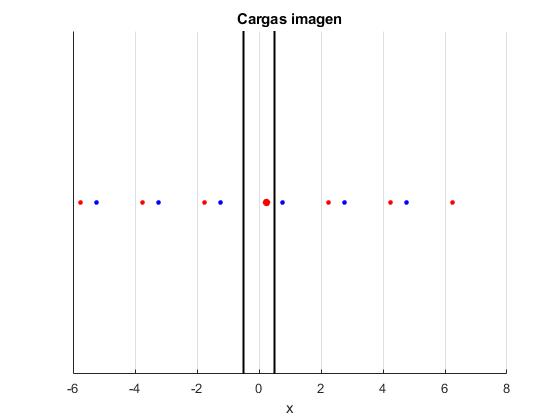
Fuerza que ejercen las cargas imagen sobre la carga +q

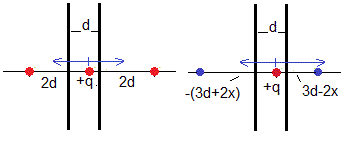
Nos daremos cuenta que las cargas imagen positivas están simétricamente dispuestas alrededor de la carga real, la fuerza que ejercen sobre dicha carga +q las cargas imágenes se anulan de dos en dos, tal como se muestra en la figura con las cargas imagen situadas en 2d y -2d.

La fuerza sobre la carga origen +q se debe únicamente a las cargas imagen negativas. Por ejemplo, la situada en -(3d+2x) produce en la carga real +q una fuerza atractiva hacia la izquerda. La situada en (3d-2x) produce en la carga real +q una fuerza hacia la derecha cuyo módulo es mayor al ser la distancia menor

La fuerza total sobre la carga origen +q es la suma

${\displaystyle \begin{array}{l}F=\frac{1}{4\pi {\epsilon }_0}\left(-\mathrm{...}-\frac{q^2}{{\left(5d+2x\right)}^2}-\frac{q^2}{{\left(3d+2x\right)}^2}-\frac{q^2}{{\left(d+2x\right)}^2}+\frac{q^2}{{\left(d-2x\right)}^2}+\frac{q^2}{{\left(3d-2x\right)}^2}+\frac{q^2}{{\left(5d-2x\right)}^2}+\mathrm{...}\right)=\hfill \\ \frac{q^2}{4\pi {\epsilon }_0}{\displaystyle \sum _{n=1}^{\infty }\left(\frac{1}{{\left((2n-1)d-2x\right)}^2}-\frac{1}{{\left((2n-1)d+2x\right)}^2}\right)=\frac{2q^2}{\pi {\epsilon }_0}xd{\displaystyle \sum _{n=1}^{\infty }\frac{2n-1}{{\left({\left(2n-1\right)}^2{d}^2-4x^2\right)}^2}}}\hfill \end{array}}$

Ejemplo

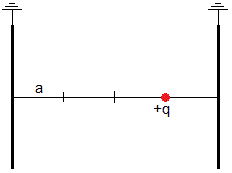
La carga +q está a una distancia x=a de la placa derecha y a 3a de la izquierda, la distancia entre las dos placas es d=4a. la fuerza sobre dicha carga vale

${\displaystyle \begin{array}{l}F=\frac{q^2}{4\pi {\epsilon }_0{a}^2}\left(-\mathrm{...}-\frac{1}{{22}^2}-\frac{1}{{14}^2}-\frac{1}{6^2}+\frac{1}{2^2}+\frac{1}{{10}^2}+\frac{1}{{18}^2}+\mathrm{...}\right)=\\ \frac{q^2}{4\pi {\epsilon }_0{a}^2}\frac{1}{4}\left(\frac{1}{1^2}-\frac{1}{3^2}+\frac{1}{5^2}-\frac{1}{7^2}+\frac{1}{9^2}-\frac{1}{{11}^2}+\mathrm{...}\right)\end{array}}$

Entre paréntesis tenemos la diferencia de dos series

${\displaystyle \begin{array}{l}\frac{1}{1^2}-\frac{1}{3^2}+\frac{1}{5^2}-\frac{1}{7^2}+\frac{1}{9^2}-\frac{1}{{11}^2}+\mathrm{...}={\displaystyle \sum _{k=1}^{\infty }\frac{1}{{\left(2(2k-1)-1\right)}^2}-{\displaystyle \sum _{k=1}^{\infty }\frac{1}{{\left(2(2k)-1\right)}^2}=}}\\ {\displaystyle \sum _{k=1}^{\infty }\frac{1}{{\left(4k-3\right)}^2}-{\displaystyle \sum _{k=1}^{\infty }\frac{1}{{\left(4k-1\right)}^2}}}\end{array}}$

Evaluamos la diferencia de las dos series utilizando Math Symbolic de MATLAB

>> syms k;
>> symsum(1/(4*k-3)^2,1,inf)-symsum(1/(4*k-1)^2,1,inf)
ans =pi^2/16 + catalan/2 - psi(1, 3/4)/16
>> double(ans)
ans =    0.9160

La fuerza F sobre la carga +q vale

${\displaystyle F=\frac{q^2}{16\pi {\epsilon }_0{a}^2}0.9160}$

Energía

Calculamos la energía potencial de la carga real +q debido a las interacciones con las cargas imagen

${\displaystyle \begin{array}{l}U=\frac{q^2}{4\pi {\epsilon }_0}\left\{\begin{array}{l}\mathrm{...}+\frac{1}{4d}+\frac{1}{2d}+\frac{1}{2d}+\frac{1}{4d}+\mathrm{...}\\ \mathrm{...}-\frac{1}{5d+2x}-\frac{1}{3d+2x}-\frac{1}{d+2x}-\frac{1}{d-2x}-\frac{1}{3d-2x}-\mathrm{...}\end{array}\right\}=\\ =-\frac{q^2}{4\pi {\epsilon }_0}{\displaystyle \sum _{n=1}^{\infty }\left(\frac{1}{(2n-1)d-2x}+\frac{1}{(2n-1)d+2x}-\frac{2}{2nd}\right)}\end{array}}$

Casos particulares

• Cuando d→∞,



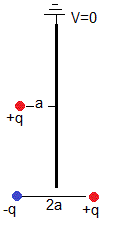
Expresamos la fuerza F en términos de la distancia a=d/2-x de la carga real +q al plano conductor derecho y calculamos el límite cuando la separación entre placas es muy grande, d→∞

${\displaystyle \begin{array}{l}F=\frac{q^2}{4\pi {\epsilon }_0}\left(\begin{array}{l}-\mathrm{...}-\frac{1}{{\left(6d-2a\right)}^2}-\frac{1}{{\left(4d-2a\right)}^2}-\frac{1}{{\left(2d-2a\right)}^2}\\ +\frac{1}{{\left(2a\right)}^2}+\frac{1}{{\left(2d+2a\right)}^2}+\frac{1}{{\left(4d+2a\right)}^2}+\mathrm{...}\end{array}\right)\\ \lim \underset{d\to \infty }{F}=\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{{\left(2a\right)}^2}\end{array}}$

Tenemos una carga +q enfrente de un plano conductor a potencial cero, que es equivalente a la carga real +q y su imagen -q situada a una distancia 2a. El valor del límite nos da la fuerza de atracción entre dichas cargas

• Cuando x=0. La carga se encuentra entre los dos planos conductores

${\displaystyle F=\frac{q^2}{4\pi {\epsilon }_0}\left(-\mathrm{...}-\frac{1}{{\left(5d\right)}^2}-\frac{1}{{\left(3d\right)}^2}-\frac{1}{d^2}+\frac{1}{d^2}+\frac{1}{{\left(3d\right)}^2}+\frac{1}{{\left(5d\right)}^2}+\mathrm{...}\right)=0}$

Equilibrio de un péndulo entre las placas de un condensador

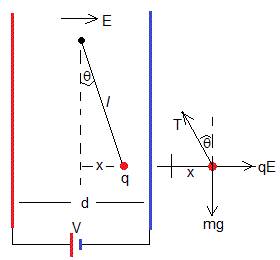
Supongamos una partícula de masa m cargada con carga +q que cuelga de un hilo de longitud l inextensible y de masa despreciable. Se sitúa el péndulo en la mitad de un condensador plano-paralelo cuyas placas están separadas d, entre las que se ha establecido una diferencia de potencial constante V. Vamos a calcular Las fuerzas sobre la carga y el desplazamiento x.

Las fuerzas que actúan sobre la partícula son:

• El peso de la partícula, mg
• La tensión T del hilo
• La fuerza qE que ejerce el campo eléctrico constante entre las placas, E=V/d

${\displaystyle \begin{array}{l}\{\begin{array}{l}T\sin \theta =qE\\ T\cos \theta =mg\end{array}\\ \tan \theta =\frac{1}{mg}qE\end{array}}$

Si el ángulo θ es pequeño, tanθ≈sinθ=x/l

${\displaystyle x\approx \left(\frac{qV}{d}\right)\frac{l}{mg}}$

Hasta aquí, la solución al problema que se propone habitualmente al estudiante de primer curso, cuando se estudia el efecto del campo eléctrico sobre las cargas

Ahora bien, una partícula cargada situada entre dos placas produce cargas imagen y hay que tener en cuenta, las fuerzas F_i entre la carga +q y sus imágenes

${\displaystyle F_i=\frac{2q^2}{\pi {\epsilon }_0}xd{\displaystyle \sum _{n=1}^{\infty }\frac{(2n-1)}{{\left({\left(2n-1\right)}^2{d}^2-4x^2\right)}^2}}}$

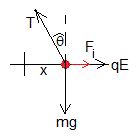
Calculamos el desplazamiento x, sabiendo que sinθ=x/l y

${\displaystyle \tan \theta =\frac{1}{mg}\left(qE+F_i\right)}$

Cuando la separación entre las placas d es mucho mayor que el desplazamiento de la partícula x, se desprecia 4x² frente a (2n-1)²d²

${\displaystyle F_i\approx \frac{2q^2}{\pi {\epsilon }_0}\frac{x}{d^3}{\displaystyle \sum _{n=1}^{\infty }\frac{1}{{\left(2n-1\right)}^3}}=\frac{2q^2}{\pi {\epsilon }_0{d}^3}x\frac{7}{8}\zeta (3)}$

Donde ζ se refiere a la función Zeta de Riemann

>> syms n;
>> symsum(1/(2*n-1)^3,1,inf)
 ans =(7*zeta(3))/8

Haciendo tanθ≈sinθ=x/l, despejamos el desplazamiento x

${\displaystyle x\approx \left(\frac{qV}{d}\right)\frac{l}{mg}{\left(1-\frac{7\zeta (3)q^2}{4\pi {\epsilon }_0{d}^3}\frac{l}{mg}\right)}^{-1}}$

Cuando el segundo término, entre paréntesis es pequeño, obtenemos la primera aproximación que no tiene en cuenta las cargas imagen. Es decir, cuando la partícula está cerca del origen, la fuerza que ejercen las cargas imagen es nula al estar simétricamente distribuidas.

Posiciones de equilibrio

La fuerza horizontal que ejerce el campo producido por las placas del condensador, las cargas imagen y la tensión de la cuerda es, F=qE+F_i-Tsinθ, que se anula cuando la partícula esta en equilibrio

${\displaystyle F=q\frac{V}{d}+\frac{2q^2}{\pi {\epsilon }_0}xd{\displaystyle \sum _{n=1}^{\infty }\frac{(2n-1)}{{\left({\left(2n-1\right)}^2{d}^2-4x^2\right)}^2}}-mg\frac{x}{\sqrt{l^2-x^2}}}$

Consideremos el siguiente dispositivo:

• Masa de la partícula, m=1 g
• Longitud del péndulo, l=6 m
• Separación entre las placas del condensador, d=1 m
• Diferencia de potencial entre las placas del condensador, V=10 000 V

Representamos la fuerza horizontal F en función de x para tres cargas +q

• q=38 nC
• q=41.3 nC
• q=70 nC

Sumamos N=10 términos de la serie, aunque bastaría con las dos cargas imágenes más próximas, N=1

m=0.001; %masa de la partícula
V=10000; %diferencia de potencial
d=1; %separación entre las placas
L=6; %longitud del hilo
N=10; %número de sumando
hold on
for q=[38,41.3,70]*1e-9
    n=1:N;
    F=@(x) q*V/d+72e9*q^2*d*x.*sum((2*n-1)./((2*n-1).^2*d^2-4*x.^2).^2)
-m*9.8*x./sqrt(L^2-x.^2);
    fplot(F, [0,0.4],'displayName',sprintf('%2.1f nC',q*1e9))
end
legend('-DynamicLegend','location','northwest')
hold off
xlabel('x')
ylabel('F')
grid on
title('Péndulo electrostático')

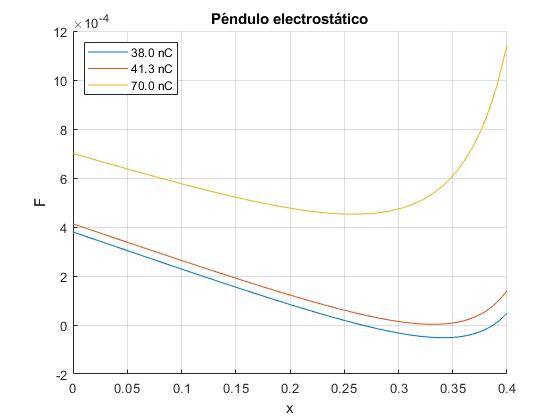
• Para q=38 nC, la fuerza F se hace cero (equilibrio) para x≈0.27 m y para x≈0.39 m

• Para q=41.3 nC, la fuerza F es tangente al eje X, hay una posición de equilibrio para x≈0.34 m.

• Para q=70 nC, la fuerza F no se anula, la partícula es acelerada hacia la placa derecha del condensador

Oscilaciones de un péndulo entre dos placas planas-paralelas conectadas a tierra

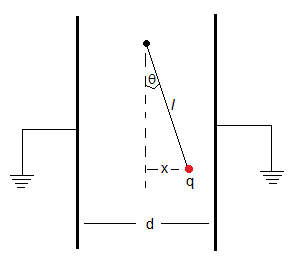
Consideremos una partícula de masa m que lleva una carga q unida a un hilo de longitud l inextensible y de masa despreciable que cuelga de un punto fijo situado en medio de dos placas conectadas a tierra.

La energía cinética de la partícula es

${\displaystyle E_k=\frac{1}{2}ml{\left(\frac{d\theta }{dt}\right)}^2}$

La energía potencial es la suma de la energía potencial gravitatoria mgl(1-cosθ) y la eléctrica U(x) que depende de x=lsinθ

La lagrangiana es

${\displaystyle \begin{array}{l}L=\frac{1}{2}m{\left(l\frac{d\theta }{dt}\right)}^2-mgl(1-\cos \theta )+\\ \frac{q^2}{4\pi {\epsilon }_0}{\displaystyle \sum _{n=1}^{\infty }\left(\frac{1}{(2n-1)d-2x}+\frac{1}{(2n-1)d+2x}-\frac{2}{2nd}\right)}\end{array}}$

La ecuación del movimiento

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ m{l}^2\frac{d^2\theta }{d{t}^2}+mgl\sin \theta -\frac{dU}{dx}l\cos \theta =0\end{array}}$

Calculamos el valor aproximado de dU(x)/dx

${\displaystyle \frac{dU}{dx}=\frac{4q^2}{\pi {\epsilon }_0}xd{\displaystyle \sum _{n=1}^{\infty }\frac{2n-1}{{\left({\left(2n-1\right)}^2{d}^2-4x^2\right)}^2}}\approx \frac{4q^2}{\pi {\epsilon }_0}\frac{x}{d^3}{\displaystyle \sum _{n=1}^{\infty }\frac{1}{{\left(2n-1\right)}^3}}}$

Ya que separación entre las placas d es mayor que el desplazamiento del péndulo x, se desprecia 4x² frente a (2n-1)²d²

Obtenemos el valor aproximado de la suma de infinitos de los términos de la serie, utilizando la función sum de MATLAB, para sumar 100 términos de la serie, o la función symsum de Math Symbolic para obtener la suma de los infinitos términos de la serie

>> n=1:100;
>> sum(1./(2*n-1).^3)
ans =    1.0518
>> clear
>> syms n;
>>  symsum(1/(2*n-1)^3,1,inf)
 ans =(7*zeta(3))/8
>> double(ans)
ans =    1.0518

Donde zeta se refiere a la función Zeta de Riemann

Teniendo en cuenta que x=lsinθ, la ecuación del movimiento se escribe

${\displaystyle m{l}^2\frac{d^2\theta }{d{t}^2}+mgl\sin \theta -\frac{4q^2}{\pi {\epsilon }_0{d}^3}k·l\sin \theta ·l\cos \theta =0}$

Con k=1.0518. Habitualmente, no conocemos la carga q de una esfera pero si conocemos el potencial V a la que ha sido cargada, la relación es

${\displaystyle V=\frac{q}{4\pi {\epsilon }_{0}R}}$

Resolvemos por procedimientos numéricos la ecuación diferencial, con las condiciones iniciales siguientes: para t=0, θ=θ₀, dθ/dt=0. El péndulo se desvía un ángulo θ₀ de la posición de equilibrio y se suelta

${\displaystyle \frac{d^2\theta }{d{t}^2}+\frac{g}{l}\sin \theta -\frac{32\pi {\epsilon }_0{R}^2{V}^2}{m{d}^3}k\sin (2\theta )=0}$

• Masa de la esfera conductora, m=0.02 kg
• Radio de la esfera conductora, R=0.02 m
• Potencial de la esfera conductora, V=10 000 V
• Longitud del hilo, l=0.5 m
• Distancia entre las placas paralelas conectadas a tierra, d=0.1 m
• El péndulo se separa un ángulo de θ₀=10° y se suelta

m=0.02; %masa
l=0.5; %longitud del hilo
V=10000; %potencial de la esfera conductora
R=0.02; %radio de la esfera
d=0.1; %separación entre placas

c=32*R^2*V^2*1.0518/(36e9*m*d^3);
fg=@(t,x)[x(2); -9.8*sin(x(1))/l+c*sin(2*x(1))];
[t,x]=ode45(fg,[0,10],[10*pi/180,0]);
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('\theta')
title('Péndulo entre dos placas')

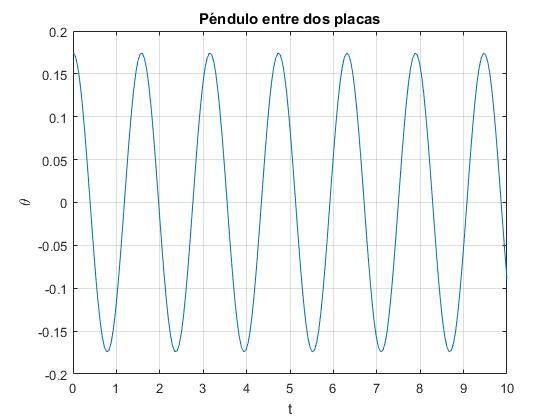
Los valores de los coeficientes de sinθ y sin(2θ) son

>> 9.8/l
ans =   19.6000
>> c
c =    1.8699

Aproximación

Cuando el ángulo θ es pequeño, aproximamos, sinθ≈θ

${\displaystyle \frac{d^2\theta }{d{t}^2}+\left(\frac{g}{l}-\frac{64\pi {\epsilon }_0{R}^2{V}^2}{m{d}^3}k\right)\theta =0}$

Se trata de la ecuación diferencial de un Movimiento Armónico Simple de frecuencia angular ω₀

${\displaystyle {\omega }_0=\sqrt{\frac{g}{l}-\frac{64\pi {\epsilon }_0{R}^2{V}^2}{m{d}^3}k}}$

Habrá oscilación siempre que el radicando sea un número positivo, lo que limita el potencial V de la esfera cargada

Referencias

D. S. Goodman, R. D. Fischetti, A. Hodges, H. A. Tekalp. Image-charge effects on an electrostatic pendulum in mechanical equilibrium. Am. J. Phys. 88(3), March 2020, pp. 222-228

Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 2058, pp. 595-598