Consideremos una carga puntual q a una distancia a de una pieza semi-infinita de dieléctrico de permitividad ε. El campo eléctrico producido por la carga q polariza el dieléctrico y aparece en su superficie una densidad de carga σ_b

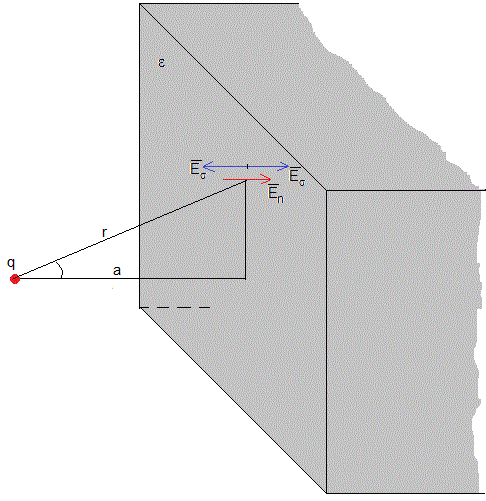
El campo eléctrico resultante en cada punto del sistema formado por la carga puntual y el dieléctrico es equivalente al producido por la carga puntual y un plano indefinido cargado con esta densidad superficial de carga σ_b como si estuvieran en el espacio vacío.

• El campo producido por la carga puntual q tiene por módulo

${\displaystyle E=\frac{1}{4\pi {\epsilon }_0}\frac{q}{r^2}}$

dirección radial y sentido hacia fuera. Su componente normal, perpendicular al plano x=a

${\displaystyle E_n=\frac{1}{4\pi {\epsilon }_0}\frac{q}{r^2}\cos \theta =\frac{1}{4\pi {\epsilon }_0}\frac{q}{a^2}{\cos }^3\theta }$

• El campo producido por el plano x=a cargado con densidad σ_b



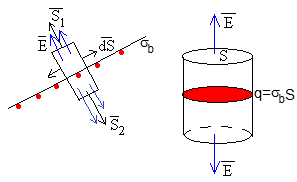
Aplicando la ley de Gauss. Tomamos una superficie cilíndrica perpendicular al plano cargado. A través de la superficie lateral no hay flujo del campo eléctrico. El flujo neto es

${\displaystyle \begin{array}{l}\overrightarrow{E}·\overrightarrow{S_1}+\overrightarrow{E}·\overrightarrow{S_2}=\frac{{\sigma }_{b}S}{{\epsilon }_0}\\ 2ES=\frac{{\sigma }_{b}S}{{\epsilon }_0},E_{\sigma }=\frac{{\sigma }_b}{2{\epsilon }_0}\end{array}}$

El campo eléctrico producido por el plano cargado es perpendicular a dicho plano

La componente del campo eléctrico resultante, perpendicular al plano, es

• Para x<a

${\displaystyle E_1=\frac{1}{4\pi {\epsilon }_0}\frac{q}{a^2}{\cos }^3\theta -\frac{{\sigma }_b}{2{\epsilon }_0}}$

• Para x>a

${\displaystyle E_2=\frac{1}{4\pi {\epsilon }_0}\frac{q}{a^2}{\cos }^3\theta +\frac{{\sigma }_b}{2{\epsilon }_0}}$

Superficie dieléctrica, x=a

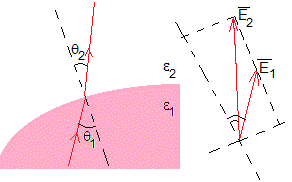
Supongamos dos medios dieléctricos de permitividades ε₁ y ε₂

El campo eléctrico cambia de módulo y dirección

La componente normal del campo, cumple, ε₁E₁cosθ₁=ε₂E₂cosθ₂. La componente tangencial, no cambia E₁sinθ₁=E₂sinθ₂

En este problema, la relación entre las componentes perpendiculares al plano dieléctrico, E₁ y E₂ es

ε₀E₁=εE₂

La permitividad relativa del dieléctrico ε_r es el cociente ε/ε₀

${\displaystyle \left(\frac{1}{4\pi {\epsilon }_0}\frac{q}{a^2}{\cos }^3\theta -\frac{{\sigma }_b}{2{\epsilon }_0}\right)={\epsilon }_r\left(\frac{1}{4\pi {\epsilon }_0}\frac{q}{a^2}{\cos }^3\theta +\frac{{\sigma }_b}{2{\epsilon }_0}\right)}$

Despejamos la densidad superficial de carga σ_b

${\displaystyle \frac{{\sigma }_b}{{\epsilon }_0}=-\left(\frac{{\epsilon }_r-1}{{\epsilon }_r+1}\right)\frac{1}{2\pi {\epsilon }_0}\frac{q}{a^2}{\cos }^3\theta }$

Potencial y campo eléctrico en un punto x<a

Calculamos el potencial y campo eléctrico producido por el plano x=a cargado en un punto P tal que x<a, a la izquierda de dicho plano

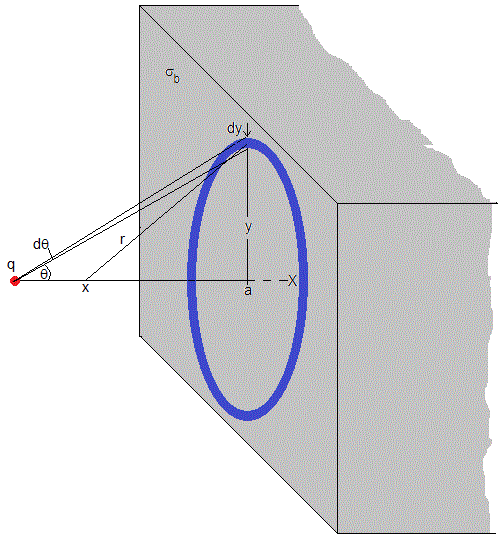
Dividimos el plano x=a del dieléctrico en anillos de radio y=atanθ, y de anchura dy=a·dθ/cos²θ. La carga dq del anillo es

${\displaystyle dq={\sigma }_b\left(2\pi y\right)dy=2\pi {\sigma }_{b}a\tan \theta \frac{a}{{\cos }^2\theta }d\theta =2\pi {\sigma }_b{a}^2\frac{\sin \theta }{{\cos }^3\theta }d\theta }$

El potencial en el punto P(x,0) es

${\displaystyle dV=\frac{1}{4\pi {\epsilon }_0}\frac{dq}{r},r=\sqrt{{\left(a-x\right)}^2+{\left(\frac{a}{\tan \theta }\right)}^2}}$

Calculamos el potencial en P producido por el plano cargado, sumando el potencial producido por los anillos

${\displaystyle \begin{array}{l}dV=\frac{{\sigma }_{b}a}{2{\epsilon }_0}\frac{\sin \theta }{{\cos }^2\theta }\frac{d\theta }{\sqrt{1-\frac{x}{a}\left(2-\frac{x}{a}\right){\cos }^2\theta }}\\ V=-\frac{q}{4\pi {\epsilon }_{0}a}\left(\frac{{\epsilon }_r-1}{{\epsilon }_r+1}\right){\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{\sin \theta ·\cos \theta }{\sqrt{1-\frac{x}{a}\left(2-\frac{x}{a}\right){\cos }^2\theta }}d\theta }\end{array}}$

La integral es inmediata, haciendo el cambio de variable, u=cos²θ, du=-2sinθcosθ·dθ

${\displaystyle {\displaystyle \int \frac{\sin \theta \cos \theta }{\sqrt{1-k{\cos }^2\theta }}d\theta }=-\frac{1}{2}{\displaystyle \int \frac{du}{\sqrt{1-ku}}}}$

Haciendo otro cambio de variable, v=1- ku, dv=-k·du

${\displaystyle {\displaystyle \int \frac{\sin \theta \cos \theta }{\sqrt{1-k{\cos }^2\theta }}d\theta }=-\frac{1}{2}{\displaystyle \int \frac{du}{\sqrt{1-ku}}}=\frac{1}{2k}{\displaystyle \int v^{-1/2}dv=}\frac{\sqrt{v}}{k}=\frac{\sqrt{1-ku}}{k}=\frac{1}{k}\sqrt{1-k{\cos }^2\theta }}$

El potencial en el punto P(x,0) debido a la distribución de carga en el plano x=a vale

${\displaystyle \begin{array}{l}V=-\frac{q}{4\pi {\epsilon }_{0}a}\left(\frac{{\epsilon }_r-1}{{\epsilon }_r+1}\right)\frac{1}{\frac{x}{a}\left(2-\frac{x}{a}\right)}\left(1-\sqrt{1-\frac{x}{a}\left(2-\frac{x}{a}\right)}\right)=-\frac{q}{4\pi {\epsilon }_{0}a}\left(\frac{{\epsilon }_r-1}{{\epsilon }_r+1}\right)\frac{1}{\frac{x}{a}\left(2-\frac{x}{a}\right)}\left(1-\left(1-\frac{x}{a}\right)\right)\\ -\frac{q}{4\pi {\epsilon }_{0}a}\left(\frac{{\epsilon }_r-1}{{\epsilon }_r+1}\right)\frac{1}{\frac{x}{a}\left(2-\frac{x}{a}\right)}\frac{x}{a}=-\frac{1}{4\pi {\epsilon }_0}\left(\frac{{\epsilon }_r-1}{{\epsilon }_r+1}\right)\frac{q}{\left(2a-x\right)}\end{array}}$

El campo eléctrico vale

${\displaystyle E=-\frac{dV}{dx}=\frac{1}{4\pi {\epsilon }_0}\left(\frac{{\epsilon }_r-1}{{\epsilon }_r+1}\right)\frac{q}{{\left(2a-x\right)}^2}}$

Este campo y potencial se pueden considerar producidos por una carga puntual imagen q₁ situada en el punto x=2a

${\displaystyle q_1=-\left(\frac{{\epsilon }_r-1}{{\epsilon }_r+1}\right)q}$

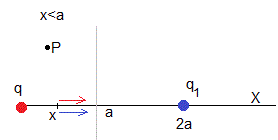
El campo y potencial en los puntos P, tales que x<a, producido por el sistema formado por una carga puntual situada a una distancia a de un diléctrico semi-infinito de permitividad ε es igual al campo y potencial producido por dicha carga puntual y otra carga q₁ imagen, de signo opuesto, situada en la posición x=2a, simétrica respecto del plano. Este sistema de dos cargas está en el vacío, permitividad ε₀

El campo resultante en un punto P(x, 0) es

${\displaystyle E_1=\frac{1}{4\pi {\epsilon }_0}\frac{q}{x^2}+\frac{1}{4\pi {\epsilon }_0}\left(\frac{{\epsilon }_r-1}{{\epsilon }_r+1}\right)\frac{q}{{\left(2a-x\right)}^2}}$

Potencial y campo eléctrico en un punto x>a

Calculamos el potencial y campo eléctrico producido por el plano x=a cargado en un punto x>a, a la derecha de dicho plano

El cálculo del potencial es análogo, la expresión de la distancia r del anillo al punto P no cambia

${\displaystyle r=\sqrt{{\left(x-a\right)}^2+{\left(\frac{a}{\tan \theta }\right)}^2}}$

Sin embargo, hemos de prestar atención a la raiz cuadrada, una vez efectuada la integral definida y antes de simplificar el resultado

${\displaystyle \begin{array}{l}V=-\frac{q}{4\pi {\epsilon }_{0}a}\left(\frac{{\epsilon }_r-1}{{\epsilon }_r+1}\right)\frac{1}{\frac{x}{a}\left(2-\frac{x}{a}\right)}\left(1-\sqrt{1-\frac{x}{a}\left(2-\frac{x}{a}\right)}\right)=-\frac{q}{4\pi {\epsilon }_{0}a}\left(\frac{{\epsilon }_r-1}{{\epsilon }_r+1}\right)\frac{1}{\frac{x}{a}\left(2-\frac{x}{a}\right)}\left(1-\left(\frac{x}{a}-1\right)\right)\\ -\frac{q}{4\pi {\epsilon }_{0}a}\left(\frac{{\epsilon }_r-1}{{\epsilon }_r+1}\right)\frac{1}{\frac{x}{a}\left(2-\frac{x}{a}\right)}\left(2-\frac{x}{a}\right)=-\frac{1}{4\pi {\epsilon }_0}\left(\frac{{\epsilon }_r-1}{{\epsilon }_r+1}\right)\frac{q}{x}\end{array}}$

El potencial debido a la carga puntual q y al plano cargado en los puntos P tales que en x>a es

${\displaystyle V=-\frac{1}{4\pi {\epsilon }_0}\left(\frac{{\epsilon }_r-1}{{\epsilon }_r+1}\right)\frac{q}{x}+\frac{1}{4\pi {\epsilon }_0}\frac{q}{x}=\frac{1}{4\pi {\epsilon }_0}\frac{2}{{\epsilon }_r+1}\frac{q}{x}=\frac{1}{4\pi \epsilon }\frac{2{\epsilon }_r}{{\epsilon }_r+1}\frac{q}{x}}$

El campo eléctrico vale

${\displaystyle E_2=-\frac{dV}{dx}=\frac{1}{4\pi \epsilon }\frac{2{\epsilon }_r}{{\epsilon }_r+1}\frac{q}{x^2}}$

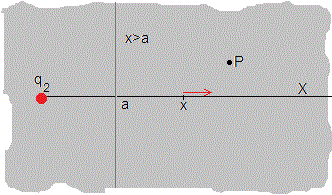
El campo y potencial en los puntos P, tales que x>a, producido por el sistema formado por una carga puntual situada a una distancia a de un diléctrico semi-infinito de permitividad ε es igual al campo y potencial producido por una carga puntual imagen q₂ situada en el origen, en la posición de la carga puntual q. Esta carga imagen está en un medio de permitividad ε

Comprobamos que en la superficie de separación x=a, los campos E₁ y E₂ están relacionados

${\displaystyle \begin{array}{l}{E}_1=\frac{1}{4\pi {\epsilon }_0}\frac{q}{a^2}+\frac{1}{4\pi {\epsilon }_0}\left(\frac{{\epsilon }_r-1}{{\epsilon }_r+1}\right)\frac{q}{a^2}=\frac{1}{4\pi {\epsilon }_0}\frac{2{\epsilon }_r}{{\epsilon }_r+1}\frac{q}{a^2}\\ E_2=\frac{1}{4\pi \epsilon }\frac{2{\epsilon }_r}{{\epsilon }_r+1}\frac{q}{a^2}\\ {\epsilon }_0{E}_1=\epsilon E_2\end{array}}$

Actividades

Se introduce

• la permitididad relativa ε_r del material dieléctrico, en el control titulado Permitididad relativa
• la distancia a entre la carga libre q y el dieléctrico, en el control titulado Distancia

Se pulsa el botón titulado Nuevo

Observamos las líneas de fuerza y las equipotenciales (en el plano XY) para los puntos P tales que x<a, en el vacío, y para x>a, en el dieléctrico

• Para los puntos x<a, corresponden al sistema formado por dos cargas q y q₁ de signo contrario, separadas una distancia 2a
• Para los puntos x>a, en el dieléctrico, corresponden a una carga q₂ situada en el origen (posición de la carga libre q). Las líneass de fuerza son rectas cuya prolongación pasa por el origen y las equipotenciales (en el plano XY) arcos de circunferencia centrados en el origen

Referencias

Taro Sometani. Kenroku Hasebe. Method for solving electrostatic problems having a simple dielectric boundary Am. J. Phys. 45 (10) October 1977, pp. 918-921

Lorrain P. Corson D. Campos y ondas electromagnéticas. Selecciones Científicas (1972), págs. 162-166