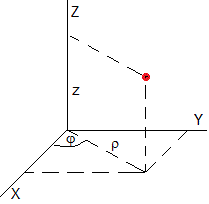
La posición de un punto en coordendas cilíndricas está especificada, por ρ, el ángulo φ y z: x=ρ·cosφ, y=ρ·sinφ, z=z

En coordenadas cilíndricas la ecuación de Laplace se escribe.

${\displaystyle \frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial V}{\partial \rho }\right)+\frac{1}{{\rho }^2}\frac{{\partial }^{2}V}{\partial {\phi }^2}+\frac{{\partial }^{2}V}{\partial z^2}=0}$

Consideremos un recinto 0≤ρ≤r, 0≤z≤h que no contiene carga. El potencial es independiente del ángulo φ. La ecuación de Laplace se escribe.

${\displaystyle \frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial V}{\partial \rho }\right)+\frac{{\partial }^{2}V}{\partial z^2}=0}$

La solución V(ρ,z) se escribe como producto de dos funciones una R(ρ) que depende solamente de ρ y otra Z(z), que depende solamente de z. V(ρ,z)=R(ρ)Z(z)

${\displaystyle \begin{array}{l}Z(z)\frac{1}{\rho }\frac{d}{d\rho }\left(\rho \frac{dR(\rho )}{d\rho }\right)+R(\rho )\frac{d^{2}Z(z)}{\partial z^2}=0\hfill \\ \frac{1}{R(\rho )}\frac{1}{\rho }\frac{d}{d\rho }\left(\rho \frac{dR(\rho )}{d\rho }\right)=-\frac{1}{Z(z)}\frac{d^{2}Z(z)}{d{z}^2}=k^2\hfill \end{array}}$

Esto da lugar a dos posibles soluciones, como en las coordenadas rectangulares. Estudiamos estas dos soluciones para dos recintos: cilíndrico y cilíndico con hueco, en los siguientes apartados:

• Primera solución
• Segunda solución

Recinto cilíndrico

Primera solución

${\displaystyle \begin{array}{l}\frac{d}{d\rho }\left(\rho \frac{dR(\rho )}{d\rho }\right)+k^2\rho R(\rho )=0\\ \frac{d^{2}Z(z)}{d{z}^2}-k^{2}Z(z)=0\end{array}}$

La solución de la segunda ecuación ya la hemos estudiado en coordenadas rectangulares

${\displaystyle Z(z)=A\sinh (kz)+B\cosh (kz)}$

Para hallar la solución de la primera, la escribimos

${\displaystyle \rho \frac{d^{2}R}{d{\rho }^2}+\frac{dR}{d\rho }+k^2\rho R=0}$

Haciendo el cambio de variable ξ=kρ

${\displaystyle \begin{array}{l}\xi \frac{d^{2}R}{d{\xi }^2}+\frac{dR}{d\xi }+\xi R=0\\ {\xi }^2\frac{d^{2}R}{d{\xi }^2}+\xi \frac{dR}{d\xi }+{\xi }^{2}R=0\end{array}}$

Que es la ecuación de Bessel con n=0. Cuya solución es

${\displaystyle R(\xi )=C{J}_0(\xi )+D{Y}_0(\xi )}$

La solución de la ecuación de Laplace es el producto

${\displaystyle V(\rho ,z)=R(\rho )Z(z)=\left(C{J}_0(k\rho )+D{Y}_0(k\rho )\right)\left(A\sinh (kz)+B\cosh (kz)\right)}$

Cuando ρ→0, Y(kρ)→∞, por tanto, se descarta este término de la solución

${\displaystyle V(\rho ,z)=R(\rho )Z(z)=C{J}_0(k\rho )\left(A\sinh (kz)+B\cosh (kz)\right)}$

Sea un recinto de forma cilíndrica de radio a y altura h

Condiciones de controrno

• Para ρ=a, V(a,z)=0
• Para z=0, V(ρ,0)=0
• Para z=h, V(ρ,h)

Para que V(a,z)=0 cuando ρ=a, se tiene que cumplir que J₀(ka)=0. En la página, titulada Funciones de Bessel se calculan las raíces α_n=k_na de la ecuación transcendente J₀(x)=0

Para que V(ρ,0)=0 cuando z=0

${\displaystyle \begin{array}{l}V(\rho \mathrm{,0})=R(\rho )Z(0)=\\ C{J}_0(k\rho )\left(A\sinh (0)+B\cosh (0)\right)=\\ BC{J}_0(k\rho )=0\end{array}}$

se tiene que cumplir que B=0

La solución de la ecuación de Laplace, V(ρ,z), es la superposición

${\displaystyle V(\rho ,z)={\displaystyle \sum _{n=1}^{\infty }{C}_n\sinh (k_{n}z)J_0}(k_n\rho )k_n=\frac{{\alpha }_n}{a}}$

Calculamos los coeficientes C_n con la condición de contorno en z=h

${\displaystyle V(\rho ,H)={\displaystyle \sum _{n=1}^{\infty }{C}_n\sinh (k_{n}H)J_0}(k_n\rho )}$

Teniendo en cuenta las relaciones de ortogonalidad

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{1}{\int }}x{J}_0({\alpha }_{m}x)J_0({\alpha }_{n}x)dx}=0m\ne n\\ {\displaystyle \underset{0}{\overset{1}{\int }}x{J}_0^2({\alpha }_{n}x)dx}=\frac{1}{2}\left(J_0^2({\alpha }_n)+J_1^2({\alpha }_n)\right)\end{array}}$

Donde α_n es la raíz n de la ecuación J₀(x)=0

Haciendo el cambio de variable, x=ρ/a, estas relaciones se transforman en las siguientes

${\displaystyle \begin{array}{l}\frac{1}{a^2}{\displaystyle \underset{0}{\overset{a}{\int }}\rho J_0(k_m\rho )J_0(k_n\rho )d\rho }=0m\ne n\\ \frac{1}{a^2}{\displaystyle \underset{0}{\overset{a}{\int }}\rho J_0^2(k_n\rho )d\rho }=\frac{1}{2}\left(J_0^2(k_{n}a)+J_1^2(k_{n}a)\right)=\frac{1}{2}{J}_1^2(k_{n}a)\end{array}}$

Los coeficientes C_n valen

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{a}{\int }}V(\rho ,h)}{J}_0(k_m\rho )d\rho ={\displaystyle \underset{0}{\overset{a}{\int }}\left({\displaystyle \sum _{n=1}^{\infty }{C}_n\sinh (k_{n}h)J_0}(k_n\rho )\right)}{J}_0(k_m\rho )d\rho \\ {\displaystyle \underset{0}{\overset{a}{\int }}\rho V(\rho ,h)}{J}_0(k_m\rho )d\rho ={\displaystyle \sum _{n=1}^{\infty }{C}_n\sinh (k_{n}h)\left\{{\displaystyle \underset{0}{\overset{a}{\int }}\rho J_0(k_n\rho )J_0(k_m\rho )d\rho }\right\}}\\ {\displaystyle \underset{0}{\overset{a}{\int }}\rho V(\rho ,h)}{J}_0(k_n\rho )d\rho =C_n\sinh (k_{n}h)\frac{a^2}{2}{J}_1^2(k_{n}a)\\ C_n=\frac{2{\displaystyle \underset{0}{\overset{a}{\int }}\rho V(\rho ,h)}{J}_0(k_n\rho )d\rho }{a^2\sinh (k_{n}h)J_1^2(k_{n}a)}\end{array}}$

Ejemplo

Consideremos el caso más sencillo, V(ρ, h)=V₀ es constante

Teniendo en cuenta la propiedad de la función de Bessel J₀

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{1}{\int }}x{J}_0({\alpha }_{n}x)dx}=\frac{1}{{\alpha }_n}{J}_1({\alpha }_n)\\ \frac{1}{a^2}{\displaystyle \underset{0}{\overset{1}{\int }}\rho J_0(k_n\rho )d\rho }=\frac{1}{k_{n}a}{J}_1(k_{n}a)\end{array}}$

La solución V(ρ,z) expresada en términos de las variables adimensionales, z/h, ρ/a

${\displaystyle \begin{array}{l}{C}_n=\frac{2V_0}{k_{n}a\sinh (k_{n}h)J_1(k_{n}a)}\\ V(\rho ,z)=2V_0{\displaystyle \sum _{n=1}^{\infty }\frac{\sinh \left({\alpha }_n\frac{h}{a}\frac{z}{h}\right)J_0\left({\alpha }_n\frac{\rho }{a}\right)}{{\alpha }_n\sinh \left({\alpha }_n\frac{h}{a}\right)J_1({\alpha }_n)}}\end{array}}$

Donde α_n es la raíz n de la ecuación J₀(x)=0

Sea un recinto en forma cilíndrica, de radio a=1, y de altura h=1

Definimos la función raices para calcular las raíces múltiples de una función f(x)

function r = raices(f, x)
    y=f(x);
    indices=find(y(1:end-1).*y(2:end)<0);
    r=zeros(1,length(indices));
    for k=1:length(indices)
        r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
    end
end

Definimos la función que calcula el potencial V(ρ,z), pasándole las primeras raíces de la ecuación transcendente J₀(x)=0

function res = laplace_potencial_7(rho,z, alfa)
    res=0;
    for n=1:length(alfa)
         res=res+2*sinh(alfa(n)*z).*besselj(0,alfa(n)*rho)/
(alfa(n)*sinh(alfa(n))*besselj(1,alfa(n)));
    end
end

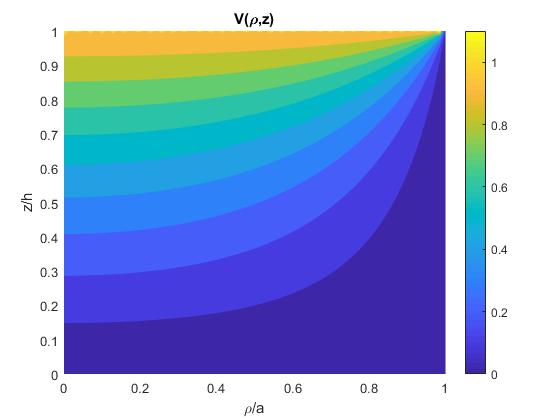
Representamos las líneas equipotenciales mediante fcontour

%Raíces de J_0(x)=0
x=linspace(0,200,200);
alfa=raices(@(x) besselj(0,x),x); 

f=@(rho,z) laplace_potencial_7(rho,z, alfa);
fcontour(f,[0,1,0,1], 'fill','on')
colorbar
xlabel('\rho/a')
ylabel('z/h')
title('V(\rho,z)')

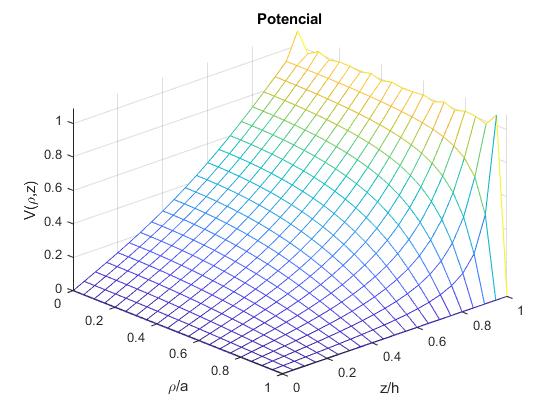
Representamos la función V(ρ,z) mediante mesh

%Raíces de J_0(x)=0
x=linspace(0,200,200);
alfa=raices(@(x) besselj(0,x),x); 

[x,y] = meshgrid(0:0.05:1, 0:0.05:1);
z=laplace_potencial_7(x,y, alfa);
mesh(x,y,z)
xlabel('\rho/a')
ylabel('z/h')
zlabel('V(\rho,z)')
title('Potencial')
view(47,32)

Segunda solución

${\displaystyle \begin{array}{l}\frac{d}{d\rho }\left(\rho \frac{dR(\rho )}{d\rho }\right)-k^2\rho R(\rho )=0\\ \frac{d^{2}Z(z)}{d{z}^2}+k^{2}Z(z)=0\end{array}}$

La solución de la segunda ecuación ya la hemos estudiado en coordenadas rectangulares

${\displaystyle Z(z)=A\sin (kz)+B\cos (kz)}$

Para encontrar la solución de la primera, hacemos el cambio de variable ξ=kρ

${\displaystyle \begin{array}{l}\xi \frac{d^{2}R}{d{\xi }^2}+\frac{dR}{d\xi }-\xi R=0\\ {\xi }^2\frac{d^{2}R}{d{\xi }^2}+\xi \frac{dR}{d\xi }-{\xi }^{2}R=0\end{array}}$

La solución de esta ecuación diferencial se expresa en términos de las funciones modificadas de Bessel I y K para n=0

${\displaystyle R(\rho )=C{I}_0(k\rho )+D{K}_0(k\rho )}$

La solución de la ecuación de Laplace es el producto

${\displaystyle V(\rho ,z)=R(\rho )Z(z)=\left(C{I}_0(k\rho )+D{K}_0(k\rho )\right)\left(A\sin (kz)+B\cos (kz)\right)}$

Cuando ρ→0, K₀(kρ)→∞, por tanto, se descarta este término de la solución

${\displaystyle V(\rho ,z)=R(\rho )Z(z)=C{I}_0(k\rho )\left(A\sin (kz)+B\cos (kz)\right)}$

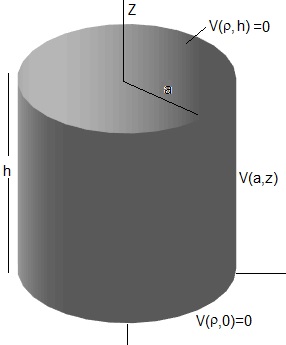
Sea un recinto de forma cilíndrica de radio a y altura h

Condiciones de controrno

• Para z=0, V(ρ,0)=0
• Para z=h, V(ρ,h)=0
• Para ρ=a, V(a,z)

La condición V(ρ,0)=0 hace que B=0,

V(ρ,0)=CI₀(kρ)B=0
B=0

Para la condición V(ρ,h)=0, se tiene que cumplir que

V(ρ,h)=CI₀(kρ)Asin(kh)=0
kh=nπ (n=1,2,3...)

La solución de la ecuación de Laplace, V(ρ,z), es la superposición

${\displaystyle V(\rho ,z)={\displaystyle \sum _{n=1}^{\infty }{C}_n\sin (k_{n}z)I_0}(k_n\rho )k_n=\frac{n\pi }{h}}$

Calculamos los coeficientes C_n con la condición de contorno en ρ=a

${\displaystyle \begin{array}{l}V(a,z)={\displaystyle \sum _{n=1}^{\infty }{C}_n\sin (k_{n}z)I_0}(k_{n}a)\\ {\displaystyle \underset{0}{\overset{h}{\int }}V(a,z)\sin (k_{m}z)dz={\displaystyle \underset{0}{\overset{h}{\int }}\left({\displaystyle \sum _{n=1}^{\infty }{C}_n\sin (k_{n}z)I_0}(k_{n}a)\right)\sin (k_{m}z)dz}}\\ {\displaystyle \underset{0}{\overset{h}{\int }}V(a,z)\sin (k_{m}z)dz={\displaystyle \sum _{n=1}^{\infty }{C}_n·I_0(k_{n}a)}{\displaystyle \underset{0}{\overset{h}{\int }}\sin (k_{n}z)\sin (k_{m}z)dz}}\\ {\displaystyle \underset{0}{\overset{h}{\int }}V(a,z)\sin (k_{n}z)dz=C_n·I_0(k_{n}a)}\frac{h}{2}\end{array}}$

El potencial V(ρ,z)

${\displaystyle V(\rho ,z)={\displaystyle \sum _{n=1}^{\infty }\frac{2{\displaystyle \underset{0}{\overset{h}{\int }}V(a,z)\sin \left(n\pi \frac{z}{h}\right)dz}}{h{I}_0\left(n\pi \frac{a}{h}\right)}\sin \left(n\pi \frac{z}{h}\right)I_0}\left(n\pi \frac{\rho }{h}\right)}$

Ejemplo

Consideremos el caso más sencillo, V(a, z)=V₀ es constante. La solución expresada en términos de las variables adimensionales, z/h, ρ/a

${\displaystyle V(\rho ,z)=4\frac{V_0}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{1}{n}\frac{I_0\left(n\pi \frac{a}{h}\frac{\rho }{a}\right)\sin \left(n\pi \frac{z}{h}\right)}{I_0\left(n\pi \frac{a}{h}\right)}}}$

Sea un recinto en forma cilíndrica, de radio a=1, y de altura h=1

Definimos la función que calcula el potencial V(ρ,z), empleando N=100 términos del desarrollo en serie

function res = laplace_potencial_8(rho,z, N)
    res=0;
    for n=1:N
         res=res+4*sin((2*n-1)*pi*z).*besseli(0,(2*n-1)*pi*rho)
/(pi*(2*n-1)*besseli(0,(2*n-1)*pi));
    end
end

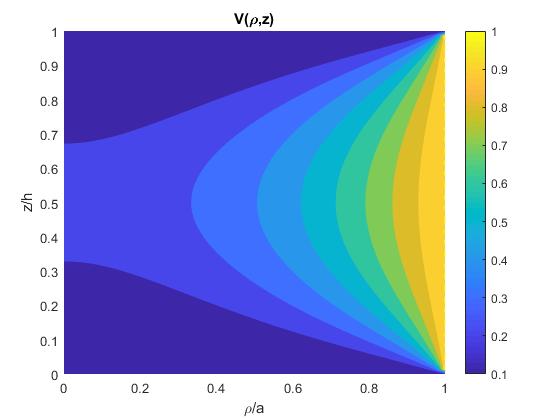
Representamos las líneas equipotenciales mediante fcontour

N=100;
f=@(rho,z) laplace_potencial_8(rho,z, N);
fcontour(f,[0,1,0,1], 'fill','on')
colorbar
xlabel('\rho/a')
ylabel('z/a')
title('V(\rho,z)')

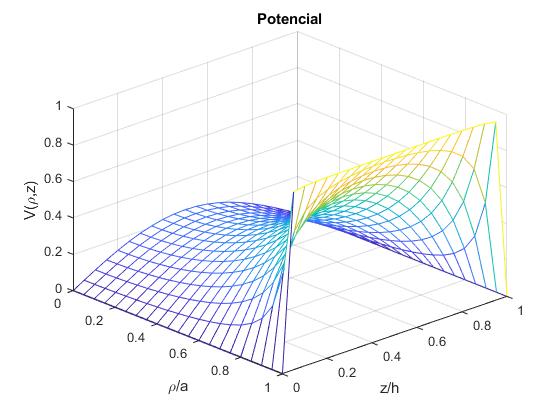
Representamos la función V(ρ,z) mediante mesh

N=100;
[x,y] = meshgrid(0:0.05:1, 0:0.05:1);
z=laplace_potencial_8(x,y, N);
mesh(x,y,z)
xlabel('\rho/a')
ylabel('z/h')
zlabel('V(\rho,z)')
title('Potencial')
view(47,32)

Cilindro hueco

Segunda solución

En un recinto cilíndrico, se descartaban de la solución V(ρ,z) los términos que se hacían infinito cuando ρ→0

• Cuando ρ→0, Y(kρ)→∞ (primera solución)

• Cuando ρ→0, K₀(kρ)→∞, (segunda solución)

En un cilindro hueco, esto ya no se puede hacer, hay que sustituirlo por la condición de contorno en la superficie cilíndrica interior

Repetimos el ejemplo anterior (segunda solucción) sustituyendo el recinto cilíndrico por uno con un hueco, tal como se muestra en la figura

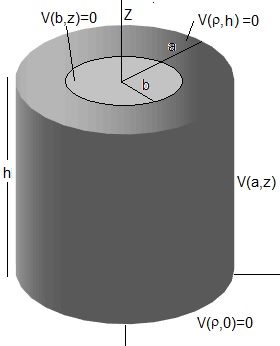
Sea un recinto de forma de cilíndro hueco de radio exterior a, interior b y altura h

Condiciones de controrno

• Para z=0, V(ρ,0)=0
• Para ρ=b, V(b, z)=0
• Para z=h, V(ρ,h)=0
• Para ρ=a, V(a,z)

La segunda solución de la ecuación de Laplace es el producto

${\displaystyle \begin{array}{l}V(\rho ,z)=R(\rho )Z(z)=\\ \left(C{I}_0(k\rho )+D{K}_0(k\rho )\right)\left(A\sin (kz)+B\cos (kz)\right)\end{array}}$

La condición V(ρ,0)=0 hace que B=0,

${\displaystyle \begin{array}{l}V(\rho \mathrm{,0})=\left(C{I}_0(k\rho )+D{K}_0(k\rho )\right)B=0\\ B=0\end{array}}$

En cuanto a la condición, V(ρ,h)=0, se tiene que cumplir que kh=nπ (n=1,2,3...).

${\displaystyle \begin{array}{l}V(\rho ,h)=\left(C{I}_0(k\rho )+D{K}_0(k\rho )\right)A\sin (kh)=0\\ k_{n}h=n\pi \end{array}}$

La condición V(b, z)=0 en el radio interior, lleva a una relación entre los coeficientes C y D

${\displaystyle C{I}_0(kb)+D{K}_0(kb)=0}$

La solución de la ecuación de Laplace, V(ρ,z), es la superposición

${\displaystyle V(\rho ,z)={\displaystyle \sum _{n=1}^{\infty }{C}_n\left(I_0(k_n\rho )-\frac{I_0(k_{n}b)}{K_0(k_{n}b)}{K}_0(k_n\rho )\right)\sin (k_{n}z)k_n=\frac{n\pi }{h}}}$

Calculamos los coeficientes C_n con la condición de contorno en ρ=a

${\displaystyle \begin{array}{l}V(a,z)={\displaystyle \sum _{n=1}^{\infty }{C}_n\sin (k_{n}z)\left(I_0(k_{n}a)-\frac{I_0(k_{n}b)}{K_0(k_{n}b)}{K}_0(k_{n}a)\right)}\\ {\displaystyle \underset{0}{\overset{h}{\int }}V(a,z)\sin (k_{m}z)dz={\displaystyle \sum _{n=1}^{\infty }{C}_n·\left(I_0(k_{n}a)-\frac{I_0(k_{n}b)}{K_0(k_{n}b)}{K}_0(k_{n}a)\right)}{\displaystyle \underset{0}{\overset{h}{\int }}\sin (k_{n}z)\sin (k_{m}z)dz}}\\ {\displaystyle \underset{0}{\overset{h}{\int }}V(a,z)\sin (k_{n}z)dz=C_n·\left(I_0(k_{n}a)-\frac{I_0(k_{n}b)}{K_0(k_{n}b)}{K}_0(k_{n}a)\right)}\frac{h}{2}\end{array}}$

El potencial V(ρ,z)

${\displaystyle V(\rho ,z)=\frac{2}{h}{\displaystyle \sum _{n=1}^{\infty }\frac{{\displaystyle \underset{0}{\overset{h}{\int }}V(a,z)\sin (k_{n}z)dz}}{\left(I_0(k_{n}a)-\frac{I_0(k_{n}b)}{K_0(k_{n}b)}{K}_0(k_{n}a)\right)}\left(I_0(k_n\rho )-\frac{I_0(k_{n}b)}{K_0(k_{n}b)}{K}_0(k_n\rho )\right)\sin (k_{n}z)}}$

Ejemplo

Consideremos el caso más sencillo, V(a, z)=V₀ es constante

${\displaystyle \begin{array}{l}V(\rho ,z)=\frac{4V_0}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{1}{n}\frac{\left(I_0\left(n\pi \frac{a}{h}\frac{\rho }{a}\right)-F_n{K}_0\left(n\pi \frac{a}{h}\frac{\rho }{a}\right)\right)}{\left(I_0\left(n\pi \frac{a}{h}\right)-F_n{K}_0\left(n\pi \frac{a}{h}\right)\right)}\sin \left(n\pi \frac{z}{h}\right)}\\ F_n=\frac{I_0\left(n\pi \frac{b}{a}\frac{a}{h}\right)}{K_0\left(n\pi \frac{b}{a}\frac{a}{h}\right)}\end{array}}$

Sea un recinto en forma de cilindro hueco, de radio interior b=0.5, exterior a=1 y de altura h=1

Definimos la función que calcula el potencial V(ρ,z), empleando N=100 términos del desarrollo en serie

function res = laplace_potencial_9(rho,z, N, b, a)
    res=0;
    for n=1:N
        Fn=besseli(0, (2*n-1)*pi*b*a)/besselk(0, (2*n-1)*pi*b*a);
         res=res+4*sin((2*n-1)*pi*z).*(besseli(0,(2*n-1)*pi*a*rho)
-Fn*besselk(0,(2*n-1)*pi*a*rho))/(pi*(2*n-1)*(besseli(0,(2*n-1)*pi*a)-
Fn*besselk(0,(2*n-1)*pi*a)));
    end
end

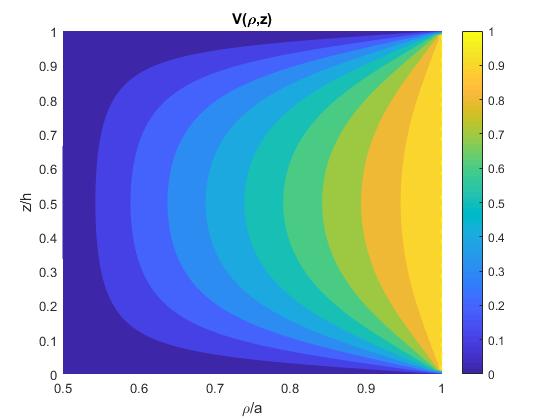
Representamos las líneas equipotenciales mediante fcontour

N=100;
b=0.5; %b/a
a=1; %a/h
f=@(rho,z) laplace_potencial_9(rho,z, N,b,a);
fcontour(f,[b,a,0,1], 'fill','on')
colorbar
xlabel('\rho/a')
ylabel('z/h')
title('V(\rho,z)')

Representamos la función V(ρ,z) mediante mesh

N=100;
b=0.5; %b/a
a=1; %a/h
[x,y] = meshgrid(b:0.05:a, 0:0.05:1);
z=laplace_potencial_9(x,y, N, b,a);
mesh(x,y,z)
xlabel('\rho/a')
ylabel('z/h')
zlabel('V(\rho,z)')
title('Potencial')
view(47,32)

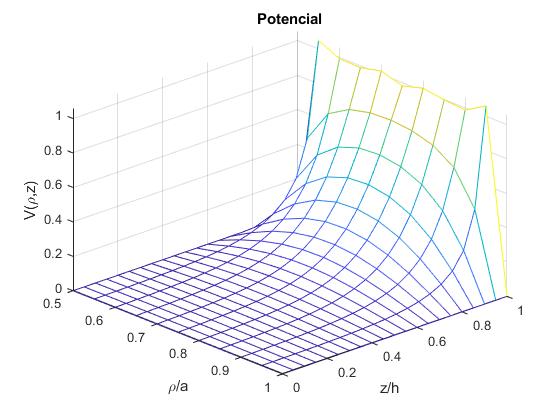
Primera solución

Repetimos el primer ejemplo (primera solución) sustituyendo el espacio cilíndrico por uno hueco. Pero veremos que el cálculo se complica notablemente

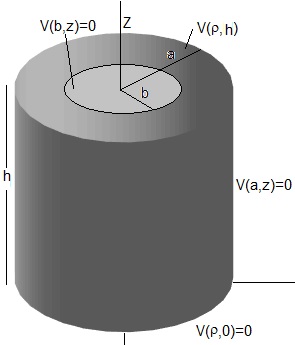
Sea un recinto en forma de cilíndro hueco de radio exterior a, interior b y altura h

Condiciones de controrno

• Para z=0, V(ρ,0)=0
• Para ρ=a, V(a,z)=0
• Para ρ=b, V(b, z)=0
• Para z=h, V(ρ,h)

La primera solución de la ecuación de Laplace es el producto

${\displaystyle \begin{array}{l}V(\rho ,z)=R(\rho )Z(z)=\\ \left(C{J}_0(k\rho )+D{Y}_0(k\rho )\right)\left(A\sinh (kz)+B\cosh (kz)\right)\end{array}}$

En un cilindro hueco, no se puede anular el coeficiente D de Y₀, hay que sustituirlo por la condición de contorno en la superficie cilíndrica interior

Las condiciones de contorno V(b, z)=0, V(a,z)=0, conducen al sistema de dos ecuaciones homogéneas

${\displaystyle \{\begin{array}{l}C{J}_0(kb)+D{Y}_0(kb)=0\\ C{J}_0(ka)+D{Y}_0(ka)=0\end{array}}$

El determinante deberá ser cero, tenemos una ecuación transcendente, cuyas raíces son α_n=k_na

${\displaystyle \begin{array}{l}{J}_0(kb)Y_0(ka)-Y_0(kb)J_0(ka)=0\\ J_0\left(\frac{\alpha }{a}b\right)Y_0(\alpha )-Y_0\left(\frac{\alpha }{a}b\right)J_0(\alpha )=0\end{array}}$

La condición V(ρ,0)=0, da lugar a B=0

${\displaystyle \begin{array}{l}V(\rho \mathrm{,0})=\left(C{J}_0(k\rho )+D{Y}_0(k\rho )\right)\left(A\sinh (0)+B\cosh (0)\right)=0\\ B=0\end{array}}$

La solución de la ecuación de Laplace V(ρ,z), es la superposición

${\displaystyle \begin{array}{l}V(\rho ,z)={\displaystyle \sum _{n=1}^{\infty }\left(C_n{J}_0(k_n\rho )+D_n{Y}_0(k_n\rho )\right)\sinh (k_{n}z)}\\ V(\rho ,z)={\displaystyle \sum _{n=1}^{\infty }{C}_n\left(J_0(k_n\rho )-\frac{J_0(k_{n}a)}{Y_0(k_{n}a)}{Y}_0(k_n\rho )\right)\sinh (k_{n}z)}=\\ {\displaystyle \sum _{n=1}^{\infty }\frac{C_n}{Y_0(k_{n}a)}\left(Y_0(k_{n}a)J_0(k_n\rho )-J_0(k_{n}a)Y_0(k_n\rho )\right)\sinh (k_{n}z)}=\\ {\displaystyle \sum _{n=1}^{\infty }\frac{C_n}{Y_0(k_{n}a)}{P}_0(k_n\rho )\sinh (k_{n}z)}\end{array}}$

P₀(k_nρ) es una combinación de dos funciones de Bessel J₀ e Y₀ que verifica:

• La propiedad de ortogonalidad

${\displaystyle {\displaystyle \underset{b}{\overset{a}{\int }}r{P}_0(k_n\rho )P_0(k_m\rho )}d\rho =\{\begin{array}{l}\mathrm{0,}m\ne n\\ m=n,\frac{2\left(J_0^2(k_{n}b)-J_0^2(k_{m}a)\right)}{{\left(\pi k_n{J}_0(k_{n}b)\right)}^2}\end{array}}$

• y esta otra propiedad

${\displaystyle {\displaystyle \underset{b}{\overset{a}{\int }}\rho P_0(k_n\rho )d\rho }=\frac{2\left(J_0(k_{n}b)-J_0(k_{n}a)\right)}{\pi k_n^2{J}_0(k_{n}b)}}$

Calculamos los coeficientes C_n con la condición de contorno en z=h

${\displaystyle \begin{array}{l}V(\rho ,h)={\displaystyle \sum _{n=1}^{\infty }\frac{C_n}{Y_0(k_{n}a)}{P}_0(k_n\rho )\sinh (k_{n}h)}\\ {\displaystyle \underset{b}{\overset{a}{\int }}\rho V(\rho ,h)P_0(k_m\rho )d\rho =}{\displaystyle \underset{b}{\overset{a}{\int }}\rho \left\{{\displaystyle \sum _{n=1}^{\infty }\frac{C_n}{Y_0(k_{n}a)}{P}_0(k_n\rho )\sinh (k_{n}h)}\right\}{P}_0(k_m\rho )d\rho }\\ {\displaystyle \underset{b}{\overset{a}{\int }}\rho V(\rho ,h)P_0(k_m\rho )d\rho }={\displaystyle \sum _{n=1}^{\infty }\frac{C_n}{Y_0(k_{n}a)}\sinh (k_{n}h){\displaystyle \underset{b}{\overset{a}{\int }}\rho P_0(k_n\rho )P_0(k_m\rho )d\rho }}\\ {\displaystyle \underset{b}{\overset{a}{\int }}\rho V(\rho ,h)P_0(k_n\rho )d\rho }=\frac{C_n}{Y_0(k_{n}a)}\sinh (k_{n}h)\frac{2\left(J_0^2(k_{n}b)-J_0^2(k_{n}a)\right)}{{\left(\pi k_n{J}_0(k_{n}b)\right)}^2}\end{array}}$

El potencial V(ρ,z)

${\displaystyle V(\rho ,z)={\displaystyle \sum _{n=1}^{\infty }\left\{\frac{{\left(\pi k_n{J}_0({\lambda }_{n}b)\right)}^2{\displaystyle \underset{b}{\overset{a}{\int }}\rho V(\rho ,h)P_0(k_n\rho )d\rho }}{2\left(J_0^2(k_{n}b)-J_0^2(k_{n}a)\right)\sinh (k_{n}h)}\right\}{P}_0(k_n\rho )\sinh (k_{n}z)}}$

Ejemplo

Consideremos el caso más sencillo, V(ρ,h)=V₀ es constante

${\displaystyle \begin{array}{l}V(\rho ,z)=\pi V_0{\displaystyle \sum _{n=1}^{\infty }\left\{\frac{J_0(k_{n}b)}{\left(J_0(k_{n}b)+J_0(k_{n}a)\right)\sinh (k_{n}h)}\right\}\left(Y_0(k_{n}a)J_0(k_n\rho )-J_0(k_{n}a)Y_0(k_n\rho )\right)\sinh (k_{n}z)}\\ V(\rho ,z)=\pi V_0{\displaystyle \sum _{n=1}^{\infty }\left\{\frac{J_0\left({\alpha }_n\frac{b}{a}\right)}{\left(J_0\left({\alpha }_n\frac{b}{a}\right)+J_0\left({\alpha }_n\right)\right)\sinh \left({\alpha }_n\frac{h}{a}\right)}\right\}\left(Y_0({\alpha }_n)J_0\left({\alpha }_n\frac{\rho }{a}\right)-J_0({\alpha }_n)Y_0\left({\alpha }_n\frac{\rho }{a}\right)\right)\sinh \left({\alpha }_n\frac{h}{a}\frac{z}{h}\right)}\end{array}}$

Sea un recinto en forma de cilindro hueco, de radio interior b=0.5, exterior a01 y de altura h=1

Calculamos las raíces de la ecuación transcendente, como en el primer apartado

b=0.5; %b/a
a=1; %a/h
%Raíces
x=linspace(0,200,200);
f=@(x) besselj(0,x*b/a).*bessely(0,x)-bessely(0,x*b/a).*besselj(0,x);
alfa=raices(f,x); 
...

Definimos la función que calcula el potencial V(ρ,z), pasándole las raíces de la ecuación transcendente

function res = laplace_potencial_10(rho,z, alfa, b, a)
    res=0;
    for n=1:length(alfa)
        Fn=pi*besselj(0,alfa(n)*b/a)/(sinh(alfa(n)/a)*(besselj(0,alfa(n)*b/a)
+besselj(0, alfa(n))));
         res=res+Fn*(bessely(0,alfa(n))*besselj(0,alfa(n)*rho/a)-
besselj(0,alfa(n))*bessely(0,alfa(n)*rho/a)).*sinh(alfa(n)*z/a);
    end
end

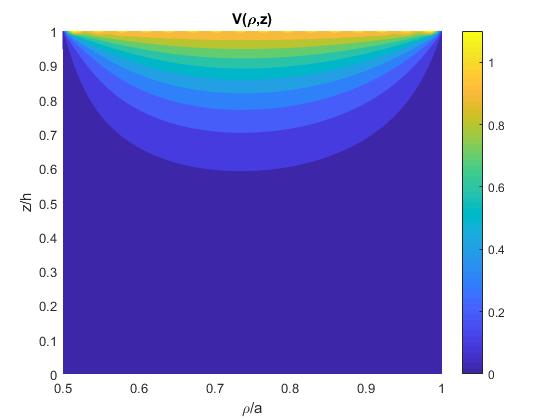
Representamos las líneas equipotenciales mediante fcontour

b=0.5; %b/a
a=1; %a/h
%Raíces
x=linspace(0,200,200);
f=@(x) besselj(0,x*b/a).*bessely(0,x)-bessely(0,x*b/a).*besselj(0,x);
alfa=raices(f,x); 

f=@(rho,z) laplace_potencial_10(rho,z, alfa,b,a);
fcontour(f,[b,a,0,1], 'fill','on')
colorbar
xlabel('\rho/a')
ylabel('z/h')
title('V(\rho,z)')

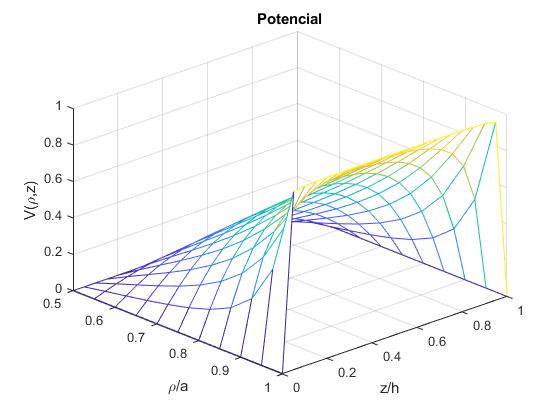
Representamos la función V(ρ,z) mediante mesh

b=0.5; %b/a
a=1; %a/h
%Raíces
x=linspace(0,200,200);
f=@(x) besselj(0,x*b/a).*bessely(0,x)-bessely(0,x*b/a).*besselj(0,x);
alfa=raices(f,x); 

[x,y] = meshgrid(b:0.05:a, 0:0.05:1);
z=laplace_potencial_10(x,y, alfa, b,a);
mesh(x,y,z)
xlabel('\rho/a')
ylabel('z/h')
zlabel('V(\rho,z)')
title('Potencial')
view(47,32)

Referencias

Larry Caretto, Solution of Laplace's Equation. College of Engineering and Computer Science. Mechanical Engineering Department. California State University. http://www.csun.edu/~lcaretto/me501b/laplace.doc. February 6, 2009