En esta página y en la siguiente, vamos a considerar situaciones con simetría alrededor de un eje Z. Utilizando coordenadas esféricas (r, θ, φ), el potencial eléctrico es independiente de φ.

La solución de la ecuación de Laplace en coordenadas esféricas es

${\displaystyle V(r,\theta )={\displaystyle \sum _{n=0}^{\infty }\left(A_n{r}^n+\frac{B_n}{r^{n+1}}\right)P_n(\cos \theta )}}$

Supongamos que es fácil calcular el potencial V(z) en los puntos del eje de simetría (por ejemplo, el anillo, el disco, la varilla uniformente cargadas). Podemos desarrollar esta función en serie de potencias de z ó 1/z

Sabiendo que para los puntos del eje Z, z>0 (θ=0) y para z<0 (θ=π) los polinomios de Legendre valen

${\displaystyle P_n(\cos \theta )=\{\begin{array}{l}\mathrm{1,}\theta =0\\ {\left(-1\right)}^n,\theta =\pi \end{array}}$

A_n y B_n se pueden determinar igualando los coeficientes en potencias de z ó 1/z de ambas series.

Conocidos los coeficientes A_n y B_n, se determina el potencial eléctrico V(r, θ) en cualquier punto del espacio.

Varilla uniformemente cargada

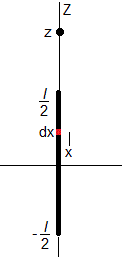
Sea una varilla de longitud l, cargada con una carga q o con una densidad de carga λ=q/l C/m. La carga dq contenida en el elemento diferencial dx comprendido entre x y x+dx produce en el punto P (0, z) situado en el eje Z un potencial

${\displaystyle \frac{1}{4\pi {\epsilon }_0}\frac{dq}{r}=\frac{1}{4\pi {\epsilon }_0}\frac{\lambda dx}{z-x}}$

El potencial V(z) producido por todos los elementos de carga de la varilla es

${\displaystyle V(z)=\frac{\lambda }{4\pi {\epsilon }_0}{\displaystyle \underset{-l/2}{\overset{l/2}{\int }}\frac{dx}{z-x}}=\frac{q}{4\pi {\epsilon }_{0}l}\left\{\ln \left(1+\frac{l}{2z}\right)-\ln \left(1-\frac{l}{2z}\right)\right\}}$

Partiendo del desarrollo en serie de las funciones ln(1+x) y ln(1-x)

${\displaystyle \ln \left(1+x\right)=x-\frac{1}{2}{x}^2+\frac{1}{3}{x}^3-\frac{1}{4}{x}^4+\mathrm{...}={\displaystyle \sum _{n=1}^{\infty }\frac{{\left(-1\right)}^{n+1}}{n}}{x}^n}$

>> syms x;
>> t1=taylor(log(1+x))
t1 =x^5/5 - x^4/4 + x^3/3 - x^2/2 + x
>> t2=taylor(log(1-x))
t2 =- x^5/5 - x^4/4 - x^3/3 - x^2/2 - x
>> t1-t2
ans =(2*x^5)/5 + (2*x^3)/3 + 2*x

La diferencia vale

${\displaystyle \begin{array}{l}\ln \left(1+\frac{l}{2z}\right)-\ln \left(1-\frac{l}{2z}\right)=2\left(\frac{l}{2z}\right)+2\frac{1}{3}{\left(\frac{l}{2z}\right)}^3+2\frac{1}{5}{\left(\frac{l}{2z}\right)}^5+\mathrm{...}\\ V(z)=\frac{q}{4\pi {\epsilon }_{0}l}{\displaystyle \sum _{n=0}^{\infty }\frac{1}{2^{2n}(2n+1)}}{\left(\frac{l}{z}\right)}^{2n+1}\end{array}}$

La solución de la ecuación de Laplace en coordenadas esféricas es

${\displaystyle V(r,\theta )={\displaystyle \sum _{n=0}^{\infty }\left(A_n{r}^n+\frac{B_n}{r^{n+1}}\right)P_n(\cos \theta )}}$

Para los puntos del espacio r>l/2. Los coeficientes A_n tiene que ser nulos para que el potencial no se haga infinito cuando r se hace grande, r→∞

${\displaystyle V(r,\theta )={\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{r^{n+1}}{P}_n(\cos \theta )}}$

El problema tiene simetría (plano z=0) por lo que solamente es necesario calcular el potencial para z>0

Para los puntos del eje Z, (z>0) el ángulo θ=0

${\displaystyle V(r\mathrm{,0})=V(z)={\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{z^{n+1}}{P}_n(1)}={\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{z^{n+1}}}=\frac{B_0}{z}+\frac{B_1}{z^2}+\frac{B_2}{z^3}+\frac{B_3}{z^4}+\frac{B_4}{z^5}+\mathrm{...}}$

Los coeficientes B_n valen

${\displaystyle \begin{array}{l}{B}_0=\frac{q}{4\pi {\epsilon }_{0}l}\\ B_1=\mathrm{0,}{B}_3=\mathrm{0,......}{B}_{2n+1}=0\\ B_{2n}=\frac{q}{4\pi {\epsilon }_0}\frac{l^{2n}}{2^n\left(2n+1\right)},n=\mathrm{1,2,3....}\end{array}}$

El potencial en los puntos del espacio (r, θ) con r>l/2 es

${\displaystyle V(r,\theta )=\frac{q}{4\pi {\epsilon }_{0}l}{\displaystyle \sum _{n=0}^{\infty }\left(\frac{1}{2^{2n}\left(2n+1\right)}{\left(\frac{l}{r}\right)}^{2n+1}\right)}{P}_{2n}(\cos \theta )}$

No se puede calcular el potencial para los puntos r<l/2

Comprobación

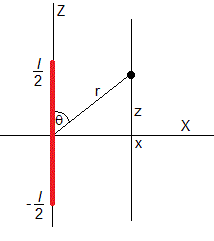
El potencial producido por una varilla de longitud l uniformemente cargada con una carga q en los puntos del plano (x, z) es

${\displaystyle V(x,z)=\frac{q}{4\pi {\epsilon }_{0}l}\ln \left(\frac{z+\frac{l}{2}+\sqrt{{\left(z+\frac{l}{2}\right)}^2+x^2}}{z-\frac{l}{2}+\sqrt{{\left(z-\frac{l}{2}\right)}^2+x^2}}\right)}$

Nota: en la página donde se ha deducido esta fórmula, el eje X es el de la varilla cargada y el eje Y es perpendicular. En este caso, el eje de la varilla es Z y el perpendicular es X. Por tanto, hemos cambiado x por z e y por x

Las coordenadas polares del punto P (x, z) son

${\displaystyle r=\sqrt{x^2+z^2},\tan \theta =\frac{x}{z}}$

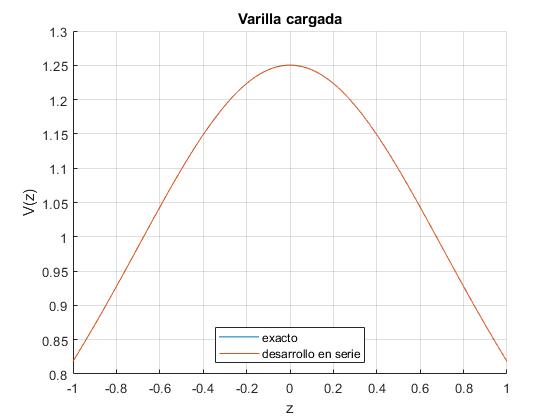
Calculamos por los dos procedimientos (exacto y desarrollo en serie), el potencial V(x, z) producido por una varilla de longitud l=1, en los puntos de la recta x=0.75 (mayor que l/2), paralela al eje Z, comprendidos entre z=-1 y z=1. Por simetría, solamente es necesario calcular el potencial en los puntos z>0

La solución de la ecuación de Laplace es la suma de infintos términos, es suficiente tomar los cinco primeros términos para que la representación gráfica de ambas expresiones del potencial V(0.75, z) coincidan, tal como se aprecia en la figura

L=1; %longitud varilla
x=0.75;
V=@(z) log((z+L/2+sqrt((z+L/2).^2+x^2))./(z-L/2+sqrt((z-L/2).^2+x^2)));
hold on
fplot(V,[-1,1])

%desarrollo en serie
zz=linspace(0,1,50);
W=zeros(1,length(zz));
i=1;
for z=zz
    th=atan(x/z);
    r=sqrt(x^2+z^2);
    for n=0:5
        W(i)=W(i)+(L/r)^(2*n+1)*legendreP(2*n,cos(th))/(2^(2*n)*(2*n+1)*L);
    end
    i=i+1;
end
plot([-fliplr(zz),zz],[fliplr(W),W]);
hold off
xlabel('z')
legend('exacto','desarrollo en serie','Location','south')
ylabel('V(z)')
grid on
title('Varilla cargada')

Superficie semiesférica, uniformemente cargada

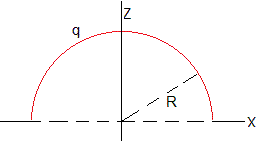
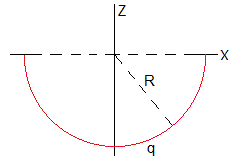
Calcularemos el potencial en el punto P situado en el eje Z producido por una superficie semiesférica de radio R, uniformemente cargada con densidad superficial σ=q/(2πR²).

En esta situación, el plano z=0 no es un plano de simetría y tendremos que calcular el potencial para z>0 y para z<0

Por otra parte, la solución de la ecuación de Laplace es distinta para r<R que para r>R. En la sección anterior, la hemos calculado para r>l/2. Tendremos que analizar cuatro situaciones distintas, dependiendo de la posición del punto P(0,z)

Primer caso, r>R

• z>0



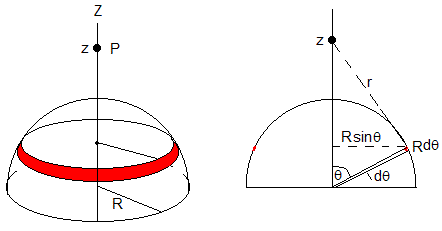
El potencial en P producido por el anillo de radio Rsinθ, y anchura R·dθ que contiene la carga dq=σ(2πRsinθ)(R·dθ) es

${\displaystyle \frac{1}{4\pi {\epsilon }_0}\frac{dq}{r}=\frac{1}{4\pi {\epsilon }_0}\frac{\sigma \left(2\pi R\sin \theta \right)\left(R·d\theta \right)}{r}}$

El potencial en P producido por todos los anillos comprendidos entre θ=0 y θ=π/2 es

${\displaystyle \begin{array}{l}V(z)=\frac{q}{4\pi {\epsilon }_0}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{\sin \theta }{\sqrt{R^2{\sin }^2\theta +{\left(z-R\cos \theta \right)}^2}}}d\theta =\frac{q}{4\pi {\epsilon }_0}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{\sin \theta }{\sqrt{R^2+z^2-2Rz\cos \theta }}}d\theta =\\ \frac{q}{4\pi {\epsilon }_0}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{1}{\sqrt{R^2+z^2-2zRu}}}du=\frac{q}{4\pi {\epsilon }_0}\frac{2}{-2zR}{\sqrt{R^2+z^2-2zRu}|}_0^1=\\ \frac{q}{4\pi {\epsilon }_0}\frac{1}{Rz}\left(\sqrt{R^2+z^2}-(z-R)\right),z>R\end{array}}$

Expresamos el potencial V(z) de la forma

${\displaystyle V(z)=\frac{q}{4\pi {\epsilon }_{0}R}\left(\sqrt{1+\frac{R^2}{z^2}}-1+\frac{R}{z}\right)}$

Desarrollamos en serie de potencias el término raíz cuadrada

${\displaystyle \begin{array}{l}{\left(1+x\right)}^n=1+nx+\frac{1}{2!}n(n-1)x^2+\frac{1}{3!}n(n-1)(n-2)x^3+\mathrm{....}+\frac{n(n-1)\mathrm{....}(n-m+1)}{m!}{x}^m+\mathrm{...}\\ {\left(1+x\right)}^{1/2}=1+\frac{1}{2}x+\frac{1}{2!}\left(\frac{1}{2}\right)\left(-\frac{1}{2}\right)x^2+\frac{1}{3!}\left(\frac{1}{2}\right)\left(-\frac{1}{2}\right)\left(-\frac{3}{2}\right)x^3+\mathrm{....}+\frac{\left(\frac{1}{2}\right)\left(-\frac{1}{2}\right)\left(-\frac{3}{2}\right)\mathrm{....}\left(\frac{1}{2}-m+1\right)}{m!}{x}^m+\mathrm{...}\\ {\left(1+x\right)}^{1/2}=1+\frac{1}{2}x-\frac{1}{2!}\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)x^2+\frac{1}{3!}\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)\left(\frac{3}{2}\right)x^3+\mathrm{....}+{\left(-1\right)}^{m-1}\frac{1·3·\mathrm{5....}\left(2m-3\right)}{2^{m}m!}{x}^m+\mathrm{...}\\ {\left(1+x\right)}^{1/2}=1+{\displaystyle \sum _{m=1}^{\infty }{\left(-1\right)}^{m-1}\frac{1·3·\mathrm{5....}\left(2m-3\right)\left(2m-1\right)}{\left(2m-1\right)2^{m}m!}{x}^m}=1-{\displaystyle \sum _{m=1}^{\infty }{\left(-1\right)}^m\frac{(2m)!}{\left(2m-1\right){\left(2^{m}m!\right)}^2}{x}^m}\end{array}}$

Math Symbolic de MATLAB nos proporciona el resultado del producto 1·3·5...·(2n-1)

>> syms n;
>> res=symprod((2*n-1),n,1,n);
>> simplify(res)
ans =factorial(2*n)/(2^n*factorial(n))

Los polinomios de Legendre cumplen

P₁(0)=P₃(0),...P_2n-1(0)=0
P₀(0)=1, P₂(0)=-1/2, P₄(0)=3/8, P₆(0)=-5/16...

${\displaystyle P_{2n}(0)={\left(-1\right)}^n\frac{(2n)!}{{\left(2^{n}n!\right)}^2}}$

>> format rat
>> P4=(-1)^2*factorial(2*2)/(2^2*factorial(2))^2
P4 =       3/8  
>> P6=(-1)^3*factorial(2*3)/(2^3*factorial(3))^2
P6 =      -5/16      

En términos de los polinomios de Legendre, el desarrollo en serie se expresa

${\displaystyle {\left(1+{\left(\frac{R}{z}\right)}^2\right)}^{1/2}=1-\frac{P_2(0)}{2·1-1}\left(\frac{R^2}{z^2}\right)-\frac{P_4(0)}{2·2-1}{\left(\frac{R^2}{z^2}\right)}^2-\frac{P_6(0)}{2·3-1}{\left(\frac{R^2}{z^2}\right)}^3-\mathrm{...}\frac{P_{2n}(0)}{2n-1}{\left(\frac{R^2}{z^2}\right)}^n}$

El desarrollo en serie del potencial V(z) es

${\displaystyle V(z)=\frac{q}{4\pi {\epsilon }_0}\left(\frac{1}{z}-\frac{1}{R}{\displaystyle \sum _{n=1}^{\infty }\frac{P_{2n}(0)}{2n-1}{\left(\frac{R}{z}\right)}^{2n}}\right)}$

Para los puntos del espacio r>R. Los coeficientes A_n de la solución de la ecuación de Laplace, tiene que ser nulos para que el potencial no se haga infinito cuando r se hace grande, r→∞

${\displaystyle V(r,\theta )={\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{r^{n+1}}{P}_n(\cos \theta )}}$

Para puntos del eje Z, tal que z>0, el ángulo θ=0

${\displaystyle V(r\mathrm{,0})=V(z)={\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{z^{n+1}}{P}_n(1)}={\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{z^{n+1}}}=\frac{B_0}{z}+{\displaystyle \sum _{n=1}^{\infty }\frac{B_n}{z^{n+1}}}}$

Los coeficientes B_n valen

${\displaystyle \begin{array}{l}{B}_0=\frac{q}{4\pi {\epsilon }_0}\\ B_2=\mathrm{0,}{B}_4=\mathrm{0,......}{B}_{2n}=0\\ B_{2n-1}=-\frac{q}{4\pi {\epsilon }_{0}R}\frac{P_{2n}(0)}{2n-1}{R}^{2n},n=\mathrm{1,2,3....}\end{array}}$

El potencial en cualquier punto del espacio (r, θ), tal que z>0 y exterior a la semiesfera r>R es

${\displaystyle V(r,\theta )=\frac{q}{4\pi {\epsilon }_{0}r}-\frac{q}{4\pi {\epsilon }_{0}R}{\displaystyle \sum _{n=1}^{\infty }\frac{P_{2n}(0)}{2n-1}{\left(\frac{R}{r}\right)}^{2n}}{P}_{2n-1}(\cos \theta )}$

• z<0



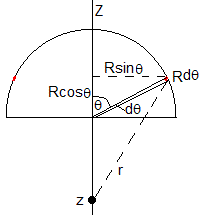
El potencial en un punto del eje Z, z<0, tal que, |z|>R

${\displaystyle \begin{array}{l}V(z)=\frac{q}{4\pi {\epsilon }_0}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{\sin \theta }{\sqrt{R^2{\sin }^2\theta +{\left(\left|z\right|+R\cos \theta \right)}^2}}}d\theta =\\ \frac{q}{4\pi {\epsilon }_0}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{1}{\sqrt{R^2+z^2+2\left|z\right|Ru}}}du=\\ \frac{q}{4\pi {\epsilon }_0}\frac{2}{2\left|z\right|R}{\sqrt{R^2+z^2+2\left|z\right|Ru}|}_0^1=\\ \frac{q}{4\pi {\epsilon }_0}\frac{1}{R\left|z\right|}\left(\left(\left|z\right|+R\right)-\sqrt{R^2+z^2}\right),\left|z\right|>R\end{array}}$

Expresamos el potencial V(z) de la forma

${\displaystyle V(z)=\frac{q}{4\pi {\epsilon }_{0}R}\left(1+\frac{R}{\left|z\right|}-\sqrt{1+\frac{R^2}{z^2}}\right)}$

El desarrollo en serie del potencial V(z) es

${\displaystyle V(z)=\frac{q}{4\pi {\epsilon }_0}\left(\frac{1}{\left|z\right|}+\frac{1}{R}{\displaystyle \sum _{n=1}^{\infty }\frac{P_{2n}(0)}{2n-1}{\left(\frac{R}{\left|z\right|}\right)}^{2n}}\right)}$

Para puntos del eje Z, tal que z<0, el ángulo θ=π, la solución de la ecuación de Laplace para r>R es

${\displaystyle V(r,\pi )=V(z)={\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{{\left|z\right|}^{n+1}}{P}_n(-1)}={\displaystyle \sum _{n=0}^{\infty }{\left(-1\right)}^n\frac{B_n}{{\left|z\right|}^{n+1}}}=\frac{B_0}{\left|z\right|}-\frac{B_1}{{\left|z\right|}^2}+\frac{B_2}{{\left|z\right|}^3}-\frac{B_3}{{\left|z\right|}^4}+\mathrm{...}}$

Los coeficientes B_n valen

${\displaystyle \begin{array}{l}{B}_0=\frac{q}{4\pi {\epsilon }_0}\\ B_2=\mathrm{0,}{B}_4=\mathrm{0,......}{B}_{2n}=0\\ B_{2n-1}=-\frac{q}{4\pi {\epsilon }_{0}R}\frac{P_{2n}(0)}{2n-1}{R}^{2n},n=\mathrm{1,2,3....}\end{array}}$

El potencial en cualquier punto del espacio (r, θ), tal que z<0 y r>R es

${\displaystyle V(r,\theta )=\frac{q}{4\pi {\epsilon }_{0}r}-\frac{q}{4\pi {\epsilon }_{0}R}{\displaystyle \sum _{n=1}^{\infty }\frac{P_{2n}(0)}{2n-1}{\left(\frac{R}{r}\right)}^{2n}}{P}_{2n-1}(\cos \theta )}$

Se obtiene la misma expresión

Segundo caso, r<R

• z>0



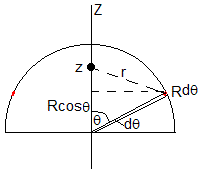
El potencial en un punto del eje Z, z>0, tal que, z<R

${\displaystyle \begin{array}{l}V(z)=\frac{q}{4\pi {\epsilon }_0}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{\sin \theta }{\sqrt{R^2+z^2-2Rz\cos \theta }}}d\theta =\\ \frac{q}{4\pi {\epsilon }_0}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{1}{\sqrt{R^2+z^2-2zRu}}}du=\frac{q}{4\pi {\epsilon }_0}\frac{2}{-2zR}{\sqrt{R^2+z^2-2zRu}|}_0^1\\ =\frac{q}{4\pi {\epsilon }_0}\frac{1}{Rz}\left(\sqrt{R^2+z^2}-\left(R-z\right)\right),z<R\end{array}}$

Expresamos el potencial V(z) de la forma

${\displaystyle V(z)=\frac{q}{4\pi {\epsilon }_{0}z}\left(\sqrt{1+\frac{z^2}{R^2}}-1+\frac{z}{R}\right)}$

El desarrollo en serie del potencial V(z) es

${\displaystyle V(z)=\frac{q}{4\pi {\epsilon }_{0}R}\left(1-{\displaystyle \sum _{n=1}^{\infty }\frac{P_{2n}(0)}{2n-1}{\left(\frac{z}{R}\right)}^{2n-1}}\right)}$

Para los puntos del espacio r<R. Los coeficientes B_n de la solución de la ecuación de Laplace, tienen que ser nulos para que el potencial no se haga infinito cuando r→0

${\displaystyle V(r,\theta )={\displaystyle \sum _{n=0}^{\infty }{A}_n{r}^n{P}_n(\cos \theta )}}$

Para puntos del eje Z, tal que z>0, el ángulo θ=0

${\displaystyle V(z\mathrm{,0})={\displaystyle \sum _{n=0}^{\infty }{A}_n{z}^n{P}_n(1)}=A_0+{\displaystyle \sum _{n=1}^{\infty }{A}_n{z}^n}}$

Los coeficientes A_n valen

${\displaystyle \begin{array}{l}{A}_0=\frac{q}{4\pi {\epsilon }_{0}R}\\ A_2=\mathrm{0,}{A}_4=\mathrm{0,......}{A}_{2n}=0\\ A_{2n-1}=-\frac{q}{4\pi {\epsilon }_0}\frac{P_{2n}(0)}{2n-1}\frac{1}{R^{2n}},n=\mathrm{1,2,3....}\end{array}}$

El potencial en cualquier punto del espacio (r, θ), tal que z>0 e interior a la semiesfera r<R es

${\displaystyle V(r,\theta )=\frac{q}{4\pi {\epsilon }_{0}R}-\frac{q}{4\pi {\epsilon }_{0}R}{\displaystyle \sum _{n=1}^{\infty }\frac{P_{2n}(0)}{2n-1}{\left(\frac{r}{R}\right)}^{2n-1}}{P}_{2n-1}(\cos \theta )}$

• z<0



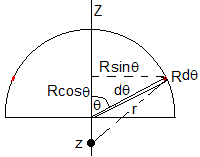
El potencial en un punto del eje Z, z<0, tal que, |z|<R

${\displaystyle \begin{array}{l}V(z)=\frac{q}{4\pi {\epsilon }_0}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{\sin \theta }{\sqrt{R^2{\sin }^2\theta +{\left(\left|z\right|+R\cos \theta \right)}^2}}}d\theta =\\ \frac{q}{4\pi {\epsilon }_0}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{1}{\sqrt{R^2+z^2+2\left|z\right|Ru}}}du=\frac{q}{4\pi {\epsilon }_0}\frac{2}{2\left|z\right|R}{\sqrt{R^2+z^2+2\left|z\right|Ru}|}_0^1=\\ \frac{q}{4\pi {\epsilon }_0}\frac{1}{R\left|z\right|}\left(\left(R+\left|z\right|\right)-\sqrt{R^2+z^2}\right),\left|z\right|<R\end{array}}$

Expresamos el potencial V(z) de la forma

${\displaystyle V(z)=\frac{q}{4\pi {\epsilon }_0\left|z\right|}\left(1+\frac{\left|z\right|}{R}-\sqrt{1+\frac{z^2}{R^2}}\right)}$

El desarrollo en serie del potencial V(z) es

${\displaystyle V(z)=\frac{q}{4\pi {\epsilon }_{0}R}\left(1+{\displaystyle \sum _{n=1}^{\infty }\frac{P_{2n}(0)}{2n-1}{\left(\frac{\left|z\right|}{R}\right)}^{2n-1}}\right)}$

Para puntos del eje Z, tal que z<0, el ángulo θ=π

${\displaystyle V(\left|z\right|,\theta )={\displaystyle \sum _{n=0}^{\infty }{A}_n{\left|z\right|}^n{P}_n(-1)}=A_0+{\displaystyle \sum _{n=1}^{\infty }{\left(-1\right)}^n{A}_n{\left|z\right|}^n}=A_0-A_1\left|z\right|+A_2{\left|z\right|}^2-A_3{\left|z\right|}^3+\mathrm{...}}$

Los coeficientes A_n valen

${\displaystyle \begin{array}{l}{A}_0=\frac{q}{4\pi {\epsilon }_{0}R}\\ A_2=\mathrm{0,}{A}_4=\mathrm{0,......}{A}_{2n}=0\\ A_{2n-1}=-\frac{q}{4\pi {\epsilon }_0}\frac{P_{2n}(0)}{2n-1}\frac{1}{R^{2n}},n=\mathrm{1,2,3....}\end{array}}$

El potencial en cualquier punto del espacio (r, θ), tal que z<0 y r<R es

${\displaystyle V(r,\theta )=\frac{q}{4\pi {\epsilon }_{0}R}-\frac{q}{4\pi {\epsilon }_{0}R}{\displaystyle \sum _{n=1}^{\infty }\frac{P_{2n}(0)}{2n-1}{\left(\frac{r}{R}\right)}^{2n-1}}{P}_{2n-1}(\cos \theta )}$

Se obtiene la misma expresión

Resumen

• Para r>R

${\displaystyle V(r,\theta )=\frac{q}{4\pi {\epsilon }_{0}r}-\frac{q}{4\pi {\epsilon }_{0}R}{\displaystyle \sum _{n=1}^{\infty }\frac{P_{2n}(0)}{2n-1}{\left(\frac{R}{r}\right)}^{2n}}{P}_{2n-1}(\cos \theta )}$

• Para r<R

${\displaystyle V(r,\theta )=\frac{q}{4\pi {\epsilon }_{0}R}-\frac{q}{4\pi {\epsilon }_{0}R}{\displaystyle \sum _{n=1}^{\infty }\frac{P_{2n}(0)}{2n-1}{\left(\frac{r}{R}\right)}^{2n-1}}{P}_{2n-1}(\cos \theta )}$

Para r=R ambas expresiones coinciden

Resultados

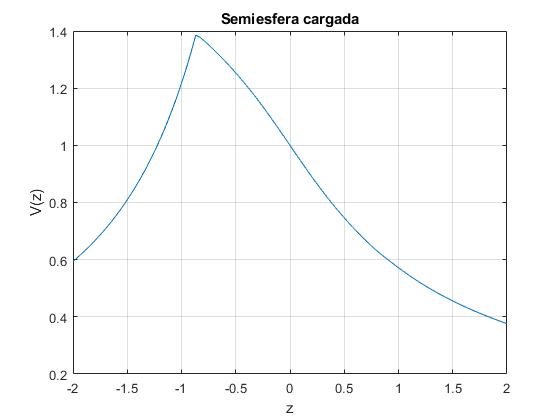
Potencial de los puntos del eje de simetría Z

Representamos el potencial eléctrico V(z) de los puntos a lo largo del eje Z. La semiesfera tiene radio R=1, asignamos a q/(4πε₀)=1

Obtenemos la misma representación gráfica, utilizando el desarrollo en serie en términos de los polinomios de Legendre. Basta tomar cinco términos pra obtener una buena aproximación. En este caso, r=|z|. Para z>0, θ=0, cosθ=1 y para z<0, θ=π, cosθ=-1

R=1; %radio semiesfera
hold on
f=@(z) (sqrt(1+(R./z).^2)-1+R./z)/R;
fplot(f,[1,2])
f=@(z) (sqrt(1+(z/R).^2)-1+z/R)./z;
fplot(f,[0,1])
f=@(z) (-sqrt(1+(z/R).^2)+1+abs(z)/R)./abs(z);
fplot(f,[-1,0])
f=@(z) (-sqrt(1+(R./z).^2)+1+R./abs(z))/R;
fplot(f,[-2,-1])

%desarrollo en serie
zz=linspace(-2,2,100);
V=zeros(1,length(zz));
i=1;
for z=zz
     r=abs(z);
    if r<R
        V(i)=1/R;
        for n=1:5
            V(i)=V(i)-legendreP(2*n,0)*(r/R)^(2*n-1)*legendreP(2*n-1,sign(z))
/(R*(2*n-1));
        end
    else
        V(i)=1/r;
        for n=1:5
            V(i)=V(i)-legendreP(2*n,0)*(R/r)^(2*n)*legendreP(2*n-1,sign(z))
/(R*(2*n-1));
        end
    end        
    i=i+1;
end
plot(zz,V,'r')
hold off
legend('exacta', 'desarrollo en serie','Location','best')
xlabel('z')
ylabel('V(z)')
grid on
title('Semiesfera cargada')

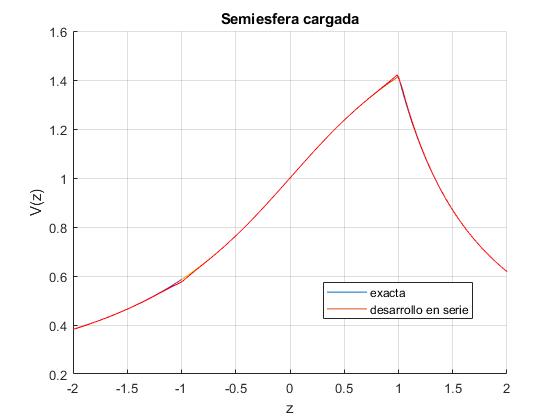
Potencial de los puntos de una recta paralela al eje Z

Representamos el potencial para los puntos de la recta paralela al eje Z, x=R/2. Cambiando a x=0, reproducimos la figura anterior

R=1; %radio semiesfera
x=R/2; %recta

zz=linspace(-2,2,100);
V=zeros(1,length(zz));
i=1;
for z=zz
    th=atan2(x,z);
    r=sqrt(x^2+z^2);
    if r<R
        V(i)=1/R;
        for n=1:5
            V(i)=V(i)-legendreP(2*n,0)*(r/R)^(2*n-1)*legendreP(2*n-1,cos(th))
/(R*(2*n-1));
        end
    else
        V(i)=1/r;
        for n=1:5
            V(i)=V(i)-legendreP(2*n,0)*(R/r)^(2*n)*legendreP(2*n-1,cos(th))
/(R*(2*n-1));
        end
    end        
    i=i+1;
end
plot(zz,V)
xlabel('z')
ylabel('V(z)')
grid on
title('Semiesfera cargada')

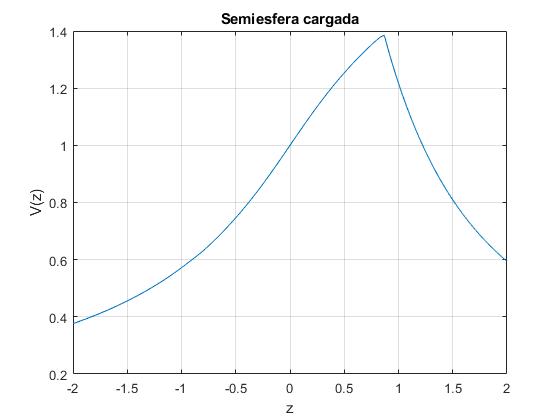
Representamos el potencial para los puntos de la recta paralela al eje Z, x=3R/2. Para todos ellos se cumple r>R

R=1; %radio semiesfera
x=3*R/2; %recta
zz=linspace(-2,2,100);
V=zeros(1,length(zz));
i=1;
for z=zz
    th=atan2(x,z);
    r=sqrt(x^2+z^2);
    V(i)=1/r;
    for n=1:5
        V(i)=V(i)-legendreP(2*n,0)*(R/r)^(2*n)*legendreP(2*n-1,cos(th))
/(R*(2*n-1));
    end
    i=i+1;
end
plot(zz,V)
xlabel('z')
ylabel('V(z)')
grid on
title('Semiesfera cargada')

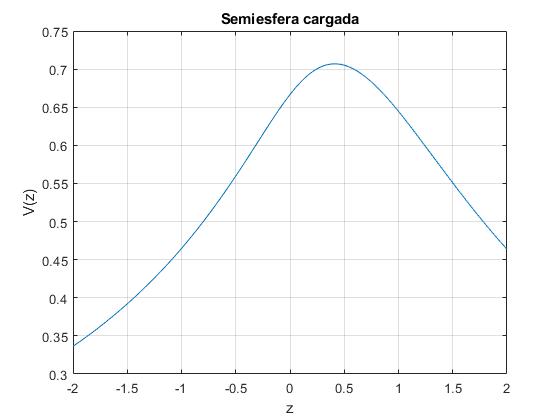
Superposición

Para representar el potencial producido por una semiesfera invertida uniformente cargada, basta hacer el cambio θ por π-θ, como puede comprobarse cambiando en los dos script anteriores la línea de código

...
    th=atan2(x,z);
....

por esta otra

...
    th=pi-atan2(x,z);
....

El resultado para la primera es

Potencial de una esfera unformemente cargada con 2q

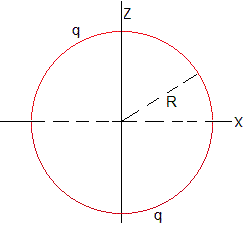
Calculamos el potencial producido por dos semiesferas iguales de radio R uniformemente cargadas con una carga q. Teniendo en cuenta que para la semiesfera inferior, cos(π-θ)=-cos(θ), y la propiedad de los polinomios de Legendre de índice impar $P_{2n-1}(-x)=-P_{2n-1}(x)$, la series infinitas se cancelan, obteniendo

${\displaystyle \begin{array}{l}V(r>R,\theta )=V(r>R,\theta )+V(r>R,\pi -\theta )=\frac{2q}{4\pi {\epsilon }_{0}r}\\ V(r<R,\theta )=V(r<R,\theta )+V(r<R,\pi -\theta )=\frac{2q}{4\pi {\epsilon }_{0}R}\end{array}}$

Resultado que que obtenemos rápidamente aplicando la ley de Gauss

Dada la simetría esférica del problema, el flujo del campo eléctrico producido por la distribución de carga a través de una superficie esférica concéntrica de radio r es E·4πr²

• La carga en el interior de una superficie esférica de radio r<R es cero, el campo eléctrico en el interior de la esfera es nulo

• La carga en el interior de una superficie esférica de radio r>R es 2q, el campo eléctrico en el exterior de la esfera es

${\displaystyle E=\frac{1}{4\pi {\epsilon }_0}\frac{2q}{r^2}}$

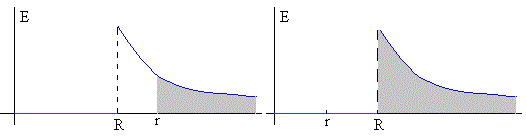
El potencial es el área sombreada, en la representación del campo eléctrico E en función de la distancia radial r

${\displaystyle \begin{array}{l}V(r>R)={\displaystyle \underset{r}{\overset{\infty }{\int }}\frac{1}{4\pi {\epsilon }_0}\frac{2q}{r^2}dr=}\frac{1}{4\pi {\epsilon }_0}\frac{2q}{r}\\ V(r<R)={\displaystyle \underset{R}{\overset{\infty }{\int }}\frac{1}{4\pi {\epsilon }_0}\frac{2q}{r^2}dr=\frac{1}{4\pi {\epsilon }_0}\frac{2q}{R}}\end{array}}$

Dipolo eléctrico

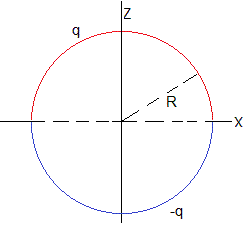
Otra situación relevante, se produce cuando las semiesferas tienen la misma carga pero de signos opuestos, un dipolo eléctrico

En la página titulada La ecuación de Laplace, coordenadas esféricas estudiamos una situación similar. Las semiesferas son conductores a potenciales iguales y opuestos

${\displaystyle \begin{array}{l}V(r>R,\theta )=\left\{\frac{q}{4\pi {\epsilon }_{0}r}-\frac{q}{4\pi {\epsilon }_{0}R}{\displaystyle \sum _{n=1}^{\infty }\frac{P_{2n}(0)}{2n-1}{\left(\frac{R}{r}\right)}^{2n}}{P}_{2n-1}(\cos \theta )\right\}+\left\{\frac{-q}{4\pi {\epsilon }_{0}r}-\frac{-q}{4\pi {\epsilon }_{0}R}{\displaystyle \sum _{n=1}^{\infty }\frac{P_{2n}(0)}{2n-1}{\left(\frac{R}{r}\right)}^{2n}}{P}_{2n-1}\left(\cos (\pi -\theta )\right)\right\}\\ =-\frac{2q}{4\pi {\epsilon }_{0}R}{\displaystyle \sum _{n=1}^{\infty }\frac{P_{2n}(0)}{2n-1}{\left(\frac{R}{r}\right)}^{2n}}{P}_{2n-1}(\cos \theta )\\ V(r<R,\theta )=\left\{\frac{q}{4\pi {\epsilon }_{0}R}-\frac{q}{4\pi {\epsilon }_{0}R}{\displaystyle \sum _{n=1}^{\infty }\frac{P_{2n}(0)}{2n-1}{\left(\frac{r}{R}\right)}^{2n-1}}{P}_{2n-1}(\cos \theta )\right\}+\left\{\frac{-q}{4\pi {\epsilon }_{0}R}-\frac{-q}{4\pi {\epsilon }_{0}R}{\displaystyle \sum _{n=1}^{\infty }\frac{P_{2n}(0)}{2n-1}{\left(\frac{r}{R}\right)}^{2n-1}}{P}_{2n-1}\left(\cos (\pi -\theta )\right)\right\}\\ =-\frac{2q}{4\pi {\epsilon }_{0}R}{\displaystyle \sum _{n=1}^{\infty }\frac{P_{2n}(0)}{2n-1}{\left(\frac{r}{R}\right)}^{2n-1}}{P}_{2n-1}(\cos \theta )\end{array}}$

Referencias

T. E. P. Bueno, U. Camara da Silva. Two methods for solving electrostatic problems with azimuthal symmetry. Revista Brasileira de Ensino de Física, vol. 42, e20190225 (2020). https://www.scielo.br/j/rbef/i/2020.v42/