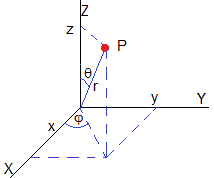
La posición de un punto en coordendas esféricas está especificada, por r, los ángulos φ y θ:

${\displaystyle \{\begin{array}{l}x=r\sin \theta \cos \phi \\ y=r\sin \theta \sin \phi \\ z=r\cos \theta \end{array}}$

La ecuación de Laplace en coordenadas esféricas es

${\displaystyle \frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial V}{\partial r}\right)+\frac{1}{r^2\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial V}{\partial \theta }\right)+\frac{1}{r^2{\sin }^2\theta }\frac{{\partial }^{2}V}{\partial {\phi }^2}=0}$

Estudiaremos solamente, aquellas situaciones en las que el potencial es V(r, θ) independiente del ángulo φ

${\displaystyle \frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial V}{\partial r}\right)+\frac{1}{r^2\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial V}{\partial \theta }\right)=0}$

La solución V(r,θ) se escribe como producto de dos funciones una R(r) que depende solamente de r y otra Θ(θ), que depende solamente de θ. V(r,θ)=R(r)Θ(θ)

${\displaystyle \begin{array}{l}\frac{\Theta (\theta )}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial R(r)}{\partial r}\right)+\frac{R(r)}{r^2\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial \Theta (\theta )}{\partial \theta }\right)=0\\ \frac{1}{R}\frac{d}{dr}\left(r^2\frac{dR}{dr}\right)+\frac{1}{\Theta \sin \theta }\frac{d}{d\theta }\left(\sin \theta \frac{d\Theta }{d\theta }\right)=0\end{array}}$

De este modo, se convierte la ecuación de Laplace en derivadas parciales en un par de ecuaciones diferenciales ordinarias, tal como se ha hecho para coordenadas rectangulares y cilíndricas, en las que hemos cambiado la constante k² por n(n+1)

${\displaystyle \begin{array}{l}\frac{d}{dr}\left(r^2\frac{dR}{dr}\right)-n(n+1)R=0\\ \frac{1}{\sin \theta }\frac{d}{d\theta }\left(\sin \theta \frac{d\Theta }{d\theta }\right)+n(n+1)\Theta =0\end{array}}$

Solución de la ecuación diferencial radial

Hacemos la sustitución r=e^x, x=lnr, quedando una ecuación diferencial de coeficientes constantes, cuya solución es inmediata.

${\displaystyle \begin{array}{l}\frac{dR}{dr}=\frac{dR}{dx}\frac{dx}{dr}=\frac{dR}{dx}\frac{1}{r}=\frac{dR}{dx}{e}^{-x}\\ \frac{d^{2}R}{d{r}^2}=\frac{d}{dr}\left(\frac{dR}{dr}\right)=\frac{d}{dx}\left(\frac{dR}{dr}\right)\frac{dx}{dr}=\frac{d}{dx}\left(\frac{dR}{dx}{e}^{-x}\right)\frac{dx}{dr}=e^{-2x}\frac{d^{2}R}{d{x}^2}-e^{-2x}\frac{dR}{dx}\\ r^2\frac{d^{2}R}{d{\rho }^2}+2r\frac{dR}{d\rho }-n(n+1)R=0\\ e^{2x}\left(e^{-2x}\frac{d^{2}R}{d{x}^2}-e^{-2x}\frac{dR}{dx}\right)+2e^x\left(\frac{dR}{dx}{e}^{-x}\right)-n(n+1)R=0\\ \frac{d^{2}R}{d{x}^2}+\frac{dR}{dx}-n(n+1)R=0\end{array}}$

La ecuación característica, s²+s-n(n+1)=0, tiene dos raíces reales distintas

${\displaystyle s=\frac{-1\pm \sqrt{1+4n(n+1)}}{2}=\{\begin{array}{l}n\\ -(n+1)\end{array}}$

La solución de la parte radial es

${\displaystyle R(r)=A{r}^n+\frac{B}{r^{n+1}}}$

Solución de la ecuación diferencial angular

${\displaystyle \frac{d^2\Theta }{d{\theta }^2}+\frac{\cos \theta }{\sin \theta }\frac{d\Theta }{d\theta }+n(n+1)\Theta =0}$

Hacemos el cambio x=cosθ

${\displaystyle \begin{array}{l}\frac{d\Theta }{d\theta }=\frac{d\Theta }{dx}\frac{dx}{d\theta }=-\frac{d\Theta }{dx}\sin \theta =-\sqrt{1-x^2}\frac{d\Theta }{dx}\\ \frac{d^2\Theta }{d{\theta }^2}=\frac{d}{d\theta }\left(\frac{d\Theta }{d\theta }\right)=\frac{d}{dx}\left(\frac{d\Theta }{d\theta }\right)\frac{dx}{d\theta }=\frac{d}{dx}\left(-\sqrt{1-x^2}\frac{d\Theta }{dx}\right)\left(-\sqrt{1-x^2}\right)=\left(1-x^2\right)\frac{d^2\Theta }{d{x}^2}-x\frac{d\Theta }{dx}\\ \frac{d^2\Theta }{d{\theta }^2}+\frac{\cos \theta }{\sin \theta }\frac{d\Theta }{d\theta }+n(n+1)\Theta =0\\ \left(1-x^2\right)\frac{d^2\Theta }{d{x}^2}-x\frac{d\Theta }{dx}+\frac{x}{\sqrt{1-x^2}}\left(-\sqrt{1-x^2}\frac{d\Theta }{dx}\right)+n(n+1)\Theta =0\\ \left(1-x^2\right)\frac{d^2\Theta }{d{x}^2}-2x\frac{d\Theta }{dx}+n(n+1)\Theta =0\end{array}}$

que es la ecuación de Legendre. Su solución es

${\displaystyle \Theta (\theta )=C·P(\cos \theta )+D·Q(\cos \theta )}$

donde P(cosθ) y Q(cosθ) son funciones de Legendre de primera y segunda especie, respectivamente. Se descartan las funciones Q, por que se hacen infinitas para cosθ=±1, o para θ=0,π. Se utilizarán las funciones Q(cosθ) en las situaciones en las que cosθ≠±1.

El potencial V(r,θ) es la superposición

${\displaystyle V(r,\theta )={\displaystyle \sum _{n=0}^{\infty }\left(A_n{r}^n+\frac{B_n}{r^{n+1}}\right)P_n(\cos \theta )}}$

En la página titulada Polinomios de Legendre, se proorciona los primeros polinomios de Legendre en términos de x=cosθ.

Estudiamos ejemplos de la aplicación de la ecuación de Laplace en coordendas esféricas con distintas condiciones de contorno

La superficie de la esfera está a un potencial que depende del ángulo θ

Supongamos que el potencial V(a,θ) de la superficie de una esfera de radio a es una función del ángulo θ.

Puntos interiores de la esfera

Vamos a calcular el potencial en un punto interior de la esfera (r<a, θ). Dado que V(r,θ) no puede se infinito cuando r→0, los coeficientes B_n=0 tienen anularse

${\displaystyle V(r,\theta )={\displaystyle \sum _{l=0}^{\infty }{A}_n{r}^n{P}_n(\cos \theta )}}$

En la superficie de la esfera

${\displaystyle V(a,\theta )={\displaystyle \sum _{n=0}^{\infty }{A}_n{a}^n{P}_n(\cos \theta )}}$

Utilizamos las relaciones de ortogonalidad de los polinomios de Legendre

${\displaystyle {\displaystyle \underset{-1}{\overset{1}{\int }}{P}_m(x)P_n(x)dx}=\{\begin{array}{l}\frac{2}{2n+1}m=n\\ 0m\ne n\end{array}}$

como x=cosθ

${\displaystyle {\displaystyle \underset{0}{\overset{\pi }{\int }}{P}_m(\cos \theta )P_n(\cos \theta )\sin \theta d\theta }=\{\begin{array}{l}\frac{2}{2n+1}m=n\\ 0m\ne n\end{array}}$

La condición de contorno en r=a nos permite calcular los coeficientes A_n

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\pi }{\int }}V(a,\theta )P_m(\cos \theta )\sin \theta ·d\theta }={\displaystyle \underset{0}{\overset{\pi }{\int }}\left({\displaystyle \sum _{n=0}^{\infty }{A}_n{a}^n{P}_n(\cos \theta )}\right)P_m(\cos \theta )\sin \theta ·d\theta }\\ {\displaystyle \underset{0}{\overset{\pi }{\int }}V(a,\theta )P_m(\cos \theta )\sin \theta ·d\theta }={\displaystyle \sum _{n=0}^{\infty }{A}_n{a}^n{\displaystyle \underset{0}{\overset{\pi }{\int }}{P}_m(\cos \theta )P_n(\cos \theta )\sin \theta ·d\theta }}\\ {\displaystyle \underset{0}{\overset{\pi }{\int }}V(a,\theta )P_n(\cos \theta )\sin \theta ·d\theta }=A_n{a}^n\frac{2}{2n+1}\end{array}}$

El potencial V(r,θ) en los puntos interiores r<a es

${\displaystyle V(r,\theta )=\frac{1}{2}{\displaystyle \sum _{n=0}^{\infty }\frac{(2n+1){\displaystyle \underset{0}{\overset{\pi }{\int }}V(a,\theta )P_n(\cos \theta )\sin \theta ·d\theta }}{a^n}{r}^n{P}_n(\cos \theta )}}$

Puntos exteriores de la esfera

Vamos a calcular el potencial en un punto exterior de la esfera (r>a, θ). Dado que V(r,θ) no puede se infinito cuando r→∞, los coeficientes A_n=0 tienen anularse

${\displaystyle V(r,\theta )={\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{r^{n+1}}{P}_n(\cos \theta )}}$

En la superficie de la esfera

${\displaystyle V(a,\theta )={\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{a^{n+1}}{P}_n(\cos \theta )}}$

Utilizamos las relaciones de ortogonalidad de los polinomios de Legendre para calcular los coeficientes B_n

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\pi }{\int }}V(a,\theta )P_m(\cos \theta )\sin \theta ·d\theta }={\displaystyle \underset{0}{\overset{\pi }{\int }}\left({\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{a^{n+1}}{P}_n(\cos \theta )}\right)P_m(\cos \theta )\sin \theta ·d\theta }\\ {\displaystyle \underset{0}{\overset{\pi }{\int }}V(a,\theta )P_m(\cos \theta )\sin \theta ·d\theta }={\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{a^{n+1}}{\displaystyle \underset{0}{\overset{\pi }{\int }}{P}_m(\cos \theta )P_n(\cos \theta )\sin \theta ·d\theta }}\\ {\displaystyle \underset{0}{\overset{\pi }{\int }}V(a,\theta )P_n(\cos \theta )\sin \theta ·d\theta }=\frac{B_n}{a^{n+1}}\frac{2}{2n+1}\end{array}}$

El potencial V(r,θ) en los puntos exteriores r>a es

${\displaystyle V(r,\theta )=\frac{1}{2}{\displaystyle \sum _{n=0}^{\infty }\left\{(2n+1)a^{n+1}{\displaystyle \underset{0}{\overset{\pi }{\int }}V(a,\theta )P_n(\cos \theta )\sin \theta ·d\theta }\right\}\frac{1}{r^{n+1}}{P}_n(\cos \theta )}}$

Ejemplo

Supongamos que el potencial en la superficie de la esfera es V(a,θ)=cos(4θ)

${\displaystyle \begin{array}{l}V(a,\theta )=\cos (4\theta )={\cos }^2(2\theta )-{\sin }^2(2\theta )=2{\cos }^2(2\theta )-1=\\ 2{\left(2{\cos }^2\theta -1\right)}^2-1=8{\cos }^4\theta -8{\cos }^2\theta +1\end{array}}$

Expresamos el polinomio f(x)=8x⁴-8x²+1, de grado 4 como combinación lineal de los cinco primeros polinomios de Legendre, f(x)=c₀P₀(x)+c₁P₁(x)+c₂P₂(x)+c₃P₃(x)+c₄P₄(x)

syms x;
p=[8,0,-8,0,1]; %coeficientes del polinomio
pol=poly2sym(p); %polinomio
for n=0:length(p)-1
    c=(2*n+1)*int(pol*legendreP(n,x),x,-1,1)/2; %coeficientes
    disp([n,c])
end

[ 0, -1/15]
[ 1, 0
[ 2, -16/21]
[ 3, 0]
[ 4, 64/35]

${\displaystyle \begin{array}{l}8x^4-8x^2+1=\frac{64}{35}{P}_4(x)-\frac{16}{21}{P}_2(x)-\frac{1}{15}{P}_0(x)\\ V(a,\theta )=8{\cos }^4\theta -8{\cos }^2\theta +1=\frac{64}{35}{P}_4(\cos \theta )-\frac{16}{21}{P}_2(\cos \theta )-\frac{1}{15}{P}_0(\cos \theta )\end{array}}$

Calculamos los coeficientes A_n y B_n, utilizando relaciones de ortogonalidad de los polinomios de Legendre

Puntos exteriores

${\displaystyle \begin{array}{l}V(r>a,\theta )=\frac{1}{2}{\displaystyle \sum _{n=0}^{\infty }\left\{(2n+1)a^{n+1}{\displaystyle \underset{0}{\overset{\pi }{\int }}\left(\frac{64}{35}{P}_4(\cos \theta )-\frac{16}{21}{P}_2(\cos \theta )-\frac{1}{15}{P}_0(\cos \theta )\right)P_n(\cos \theta )\sin \theta ·d\theta }\right\}\frac{1}{r^{n+1}}{P}_n(\cos \theta )}=\\ \frac{1}{2}9\frac{64}{35}\frac{2}{9}\frac{a^5}{r^5}{P}_4(\cos \theta )-\frac{1}{2}5\frac{16}{21}\frac{2}{5}\frac{a^3}{r^3}{P}_2(\cos \theta )-\frac{1}{2}1\frac{1}{15}\frac{2}{1}\frac{a}{r}{P}_0(\cos \theta )\end{array}}$

El resultado es

${\displaystyle V(r>a,\theta )=\frac{64}{35}{\left(\frac{a}{r}\right)}^5{P}_4(\cos \theta )-\frac{16}{21}{\left(\frac{a}{r}\right)}^3{P}_2(\cos \theta )-\frac{1}{15}\frac{a}{r}}$

Puntos interiores

${\displaystyle \begin{array}{l}V(r,\theta )=\frac{1}{2}{\displaystyle \sum _{n=0}^{\infty }\frac{(2n+1){\displaystyle \underset{0}{\overset{\pi }{\int }}\left(\frac{64}{35}{P}_4(\cos \theta )-\frac{16}{21}{P}_2(\cos \theta )-\frac{1}{15}{P}_0(\cos \theta )\right)P_n(\cos \theta )\sin \theta ·d\theta }}{a^n}{r}^n{P}_n(\cos \theta )=}\\ \frac{1}{2}9\frac{64}{35}\frac{2}{9}{\left(\frac{r}{a}\right)}^4{P}_4(\cos \theta )-\frac{1}{2}5\frac{16}{21}\frac{2}{5}{\left(\frac{r}{a}\right)}^2{P}_2(\cos \theta )-\frac{1}{2}1\frac{1}{15}\frac{2}{1}{P}_0(\cos \theta )\end{array}}$

El resultado es

${\displaystyle V(r<a,\theta )=\frac{64}{35}{\left(\frac{r}{a}\right)}^4{P}_4(\cos \theta )-\frac{16}{21}{\left(\frac{r}{a}\right)}^2{P}_2(\cos \theta )-\frac{1}{15}}$

Cuando r=a, ambas expresiones (interior y exterior) coinciden

Condensador formado por dos mitades de esfera a potenciales iguales y opuestos

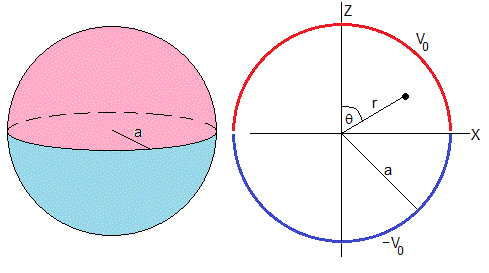
Consideremos una superficie esférica de radio a, dividida en dos mitades, la mitad superior está a potencial V₀ y la mitad inferior a -V₀. Las condiciones de contorno son:

${\displaystyle V(a,\theta )=\{\begin{array}{l}{V}_{0}0\le \theta <\frac{\pi }{2}\\ -V_0\frac{\pi }{2}<\theta \le \pi \end{array}}$

El potencial V(r,θ) es

${\displaystyle V(r,\theta )={\displaystyle \sum _{n=0}^{\infty }\left(A_n{r}^n+\frac{B_n}{r^{n+1}}\right)P_n(\cos \theta )}}$

Vamos a calcular el potencial en los puntos interiores y exteriores de la esfera.

Puntos interiores de la esfera

Vamos a calcular el potencial en un punto interior de la esfera (r<a, θ). Dado que V(r,θ) no puede se infinito cuando r→0, los coeficientes B_n=0 tienen anularse

${\displaystyle V(r,\theta )={\displaystyle \sum _{n=0}^{\infty }{A}_n{r}^n{P}_n(\cos \theta )}}$

En la superficie de la esfera

${\displaystyle V(a,\theta )={\displaystyle \sum _{n=0}^{\infty }{A}_n{a}^n{P}_n(\cos \theta )}}$

Utilizamos las relaciones de ortogonalidad de los polinomios de Legendre para calcular los coeficientes A_n

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\pi }{\int }}V(a,\theta )P_m(\cos \theta )\sin \theta ·d\theta }={\displaystyle \underset{0}{\overset{\pi }{\int }}\left({\displaystyle \sum _{n=0}^{\infty }{A}_n{a}^n{P}_n(\cos \theta )}\right)P_m(\cos \theta )\sin \theta ·d\theta }\\ V_0{\displaystyle \underset{0}{\overset{\pi /2}{\int }}{P}_m(\cos \theta )\sin \theta ·d\theta }-V_0{\displaystyle \underset{\pi /2}{\overset{\pi }{\int }}{P}_m(\cos \theta )\sin \theta ·d\theta }={\displaystyle \sum _{n=0}^{\infty }{A}_n{a}^n}{\displaystyle \underset{0}{\overset{\pi }{\int }}{P}_n(\cos \theta )P_m(\cos \theta )\sin \theta ·d\theta }\\ V_0\left({\displaystyle \underset{0}{\overset{1}{\int }}{P}_n(x)dx-{\displaystyle \underset{-1}{\overset{0}{\int }}{P}_n(x)dx}}\right)=A_n{a}^n\frac{2}{2n+1}\\ A_n=\frac{2n+1}{2}\frac{V_0\left({\displaystyle \underset{0}{\overset{1}{\int }}{P}_n(x)dx-{\displaystyle \underset{-1}{\overset{0}{\int }}{P}_n(x)dx}}\right)}{a^n}=\{\begin{array}{l}0n\text{par}\\ A_n=(2n+1)\frac{V_0{\displaystyle \underset{0}{\overset{1}{\int }}{P}_n(x)dx}}{a^n}n\text{impar}\end{array}\end{array}}$

En la representación gráfica de lospolinomios de Legendre nos daremos cuenta que para n par, P_n(x) es simétrica, para n impar, P_n(x) es antisimétrica. La diferencia entre las dos integrales es cero en el primer caso, y doble en el segundo.

syms x;
for n=0:8
    c=int(legendreP(n,x),0,1)- int(legendreP(n,x),-1,0);
    disp([n,c])
end

[ 0, 0]
[ 1, 1]
[ 2, 0]
[ 3, -1/4]
[ 4, 0]
[ 5, 1/8]
[ 6, 0]
[ 7, -5/64]
[ 8, 0]

El potencial V(r,θ) en los puntos interiores r<a es

${\displaystyle V(r,\theta )=V_0{\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }(2n+1)\left({\displaystyle \underset{0}{\overset{1}{\int }}{P}_n(x)dx}\right){\left(\frac{r}{a}\right)}^n{P}_n(\cos \theta )}}$

Calculamos los coeficientes c_n

${\displaystyle c_n=(2n+1)\left({\displaystyle \underset{0}{\overset{1}{\int }}{P}_n(x)dx}\right)}$

syms x;
for n=1:2:21 
    c=(2*n+1)*int(legendreP(n,x),0,1);
    disp([n,c])
end

[ 1, 3/2]
[ 3, -7/8]
[ 5, 11/16]
[ 7, -75/128]
[ 9, 133/256]

Los primeros términos del desarrollo en serie son

${\displaystyle \frac{V(r,\theta )}{V_0}=\frac{3}{2}\left(\frac{r}{a}\right)P_1(\cos \theta )-\frac{7}{8}{\left(\frac{r}{a}\right)}^3{P}_3(\cos \theta )+\frac{11}{16}{\left(\frac{r}{a}\right)}^5{P}_5(\cos \theta )+\mathrm{...}}$

Puntos exteriores de la esfera

Vamos a calcular el potencial en un punto exterior de la esfera (r>a, θ). Dado que V(r,θ) no puede se infinito cuando r→∞, los coeficientes A_n=0 tienen anularse

${\displaystyle V(r,\theta )={\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{r^{n+1}}{P}_n(\cos \theta )}}$

En la superficie de la esfera

${\displaystyle V(a,\theta )={\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{a^{n+1}}{P}_n(\cos \theta )}}$

Utilizamos las relaciones de ortogonalidad de los polinomios de Legendre para calcular los coeficientes B_n

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\pi }{\int }}V(a,\theta )P_m(\cos \theta )\sin \theta ·d\theta }={\displaystyle \underset{0}{\overset{\pi }{\int }}\left({\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{a^{n+1}}{P}_n(\cos \theta )}\right)P_m(\cos \theta )\sin \theta ·d\theta }\\ V_0{\displaystyle \underset{0}{\overset{\pi /2}{\int }}{P}_m(\cos \theta )\sin \theta ·d\theta }-V_0{\displaystyle \underset{\pi /2}{\overset{\pi }{\int }}{P}_m(\cos \theta )\sin \theta ·d\theta }={\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{a^{n+1}}}{\displaystyle \underset{0}{\overset{\pi }{\int }}{P}_n(\cos \theta )P_m(\cos \theta )\sin \theta ·d\theta }\\ V_0\left({\displaystyle \underset{0}{\overset{1}{\int }}{P}_n(x)dx-{\displaystyle \underset{-1}{\overset{0}{\int }}{P}_n(x)dx}}\right)=\frac{B_n}{a^{n+1}}\frac{2}{2n+1}\\ B_n=(2n+1)a^{n+1}{V}_0{\displaystyle \underset{0}{\overset{1}{\int }}{P}_n(x)dx}\end{array}}$

El potencial V(r,θ) en los puntos exteriores r>a es

${\displaystyle V(r,\theta )=V_0{\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }(2n+1)\left({\displaystyle \underset{0}{\overset{1}{\int }}{P}_n(x)dx}\right){\left(\frac{a}{r}\right)}^{n+1}{P}_n(\cos \theta )}=V_0{\displaystyle \sum _{n=0}^{\infty }{c}_n{\left(\frac{a}{r}\right)}^{n+1}{P}_n(\cos \theta )}}$

Los coeficientes c_n se han calculado para los puntos interiores

Los primeros términos del desarrollo en serie son

${\displaystyle \frac{V(r,\theta )}{V_0}=\frac{3}{2}{\left(\frac{a}{r}\right)}^2{P}_1(\cos \theta )-\frac{7}{8}{\left(\frac{a}{r}\right)}^4{P}_3(\cos \theta )+\frac{11}{16}{\left(\frac{a}{r}\right)}^6{P}_5(\cos \theta )+\mathrm{...}}$

Cuando r=a, ambas expresiones (interior y exterior) coinciden

Representamos V(a,θ)/V₀ en función de θ, tomando N=11 términos del desarrollo en serie

syms x V;
V=0;
for n=1:2:21 
    c=(2*n+1)*int(legendreP(n,x),0,1);
    V=V+c*legendreP(n,x);
end
fplot(V,[-1,1])
set(gca,'XTick',-1:0.5:1)
set(gca,'XTickLabel',{'\pi', '3\pi/4','\pi/2','\pi/4', '0'})
set(gca, 'XDir','reverse')

grid on
xlabel('\theta')
ylabel('V/V_0')
title('Potencial para r=a')

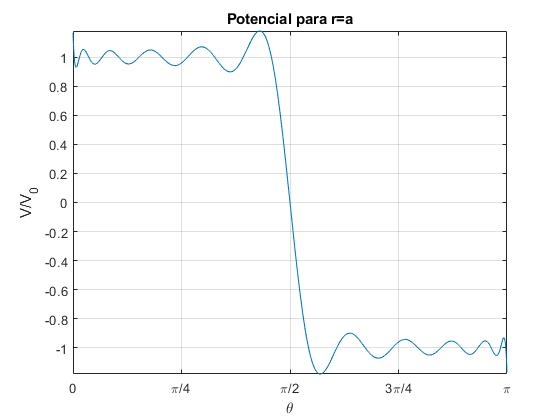
La suma se va aproximando a la condición de contorno

${\displaystyle V(a,\theta )=\{\begin{array}{l}{V}_{0}0\le \theta <\frac{\pi }{2}\\ -V_0\frac{\pi }{2}<\theta \le \pi \end{array}}$

Referencias

How to Solve Laplace's Equation in Spherical Coordinates