Anillo cargado

Vamos a calcular el potencial en el punto P producido por un anillo de radio a cargado con carga q. En la página titulada Campo y potencial eléctrico de una distribución continua de carga calculamos el potencial en un punto P del eje, θ=0, del anillo, distante r.

${\displaystyle V(r\mathrm{,0})=\frac{1}{4\pi {\epsilon }_0}\frac{q}{\sqrt{a^2+r^2}}=\frac{q}{4\pi {\epsilon }_{0}a}\frac{1}{\sqrt{1+\frac{r^2}{a^2}}}}$

Puntos P que distan r<a del centro del anillo

Para estos puntos, el coeficiente B_n=0, para evitar que el potencial se haga infinito cuando r→0

${\displaystyle V_{r<a}(r,\theta )={\displaystyle \sum _{n=0}^{\infty }{A}_n{r}^n{P}_n(\cos \theta )}}$

El desarrollo en serie de (1+x)ⁿ con el exponente n=-1/2 es

${\displaystyle \begin{array}{l}{\left(1+x\right)}^n=1+nx+\frac{1}{2!}n(n-1)x^2+\frac{1}{3!}n(n-1)(n-2)x^3+\mathrm{....}+\frac{n(n-1)\mathrm{....}(n-m+1)}{m!}{x}^m+\mathrm{...}\\ {\left(1+x\right)}^{-1/2}=1-\frac{1}{2}x+\frac{1}{2!}\left(-\frac{1}{2}\right)\left(-\frac{3}{2}\right)x^2+\frac{1}{3!}\left(-\frac{1}{2}\right)\left(-\frac{3}{2}\right)\left(-\frac{5}{2}\right)x^3+\mathrm{....}+\frac{\left(-\frac{1}{2}\right)\left(-\frac{3}{2}\right)\mathrm{....}\left(-\frac{1}{2}-m+1\right)}{m!}{x}^m+\mathrm{...}\end{array}}$

El desarrollo en serie del potencial V(r,0) en un punto P del eje es proporcional a

${\displaystyle \begin{array}{l}{\left(1+{\left(\frac{r}{a}\right)}^2\right)}^{-1/2}=1-\frac{1}{2}{\left(\frac{r}{a}\right)}^2+{\left(-1\right)}^2\frac{1}{2!}\frac{1·3}{2^2}{\left(\frac{r}{a}\right)}^4+{\left(-1\right)}^3\frac{1}{3!}\frac{1·3·5}{2^{{}^3}}{\left(\frac{r}{a}\right)}^6+\mathrm{....}+{\left(-1\right)}^m\frac{1}{m!}\frac{1·3·\mathrm{5...}(2m-1)}{2^m}{\left(\frac{r}{a}\right)}^{2m}+\mathrm{...}\\ {\left(1+{\left(\frac{r}{a}\right)}^2\right)}^{-1/2}=1-\frac{1}{2}{\left(\frac{r}{a}\right)}^2+\frac{3}{8}{\left(\frac{r}{a}\right)}^4-\frac{5}{16}{\left(\frac{r}{a}\right)}^6+\mathrm{...}{\left(-1\right)}^m\frac{(2m)!}{2^{m}m!·2^{m}m!}{\left(\frac{r}{a}\right)}^{2m}+\mathrm{...}\end{array}}$

Math Symbolic de MATLAB nos proporciona el resultado del producto 1·3·5...·(2n-1)

>> syms n;
>> res=symprod((2*n-1),n,1,n);
>> simplify(res)
ans =factorial(2*n)/(2^n*factorial(n))

Los polinomios de Legendre cumplen

P₁(0)=P₃(0),...P_2n-1(0)=0
P₀(0)=1, P₂(0)=-1/2, P₄(0)=3/8, P₆(0)=-5/16...

${\displaystyle P_{2n}(0)={\left(-1\right)}^n\frac{(2n)!}{{\left(2^{n}n!\right)}^2}}$

>> format rat
>> P4=(-1)^2*factorial(2*2)/(2^2*factorial(2))^2
P4 =       3/8  
>> P6=(-1)^3*factorial(2*3)/(2^3*factorial(3))^2
P6 =      -5/16      

En términos de los polinomios de Legendre, el desarrollo en serie se expresa

${\displaystyle {\left(1+{\left(\frac{r}{a}\right)}^2\right)}^{-1/2}=P_0(0)+P_2(0){\left(\frac{r}{a}\right)}^2+P_4(0){\left(\frac{r}{a}\right)}^4+P_6(0){\left(\frac{r}{a}\right)}^6+\mathrm{...}{P}_{2n}(0){\left(\frac{r}{a}\right)}^{2n}}$

Comparando el potencial en un punto del eje del anillo, V(r, 0) con la solución de la ecuación de Laplace para los puntos del eje del anillo θ=0, obtenemos los valores de los coeficientes A_n. Teniendo en cuenta que P_n(1)=1

${\displaystyle \begin{array}{l}V(r\mathrm{,0})={\displaystyle \sum _{l=0}^{\infty }{A}_n{r}^n{P}_n(1)}={\displaystyle \sum _{l=0}^{\infty }{A}_n{r}^n}\\ \{\begin{array}{l}{A}_1=\mathrm{0,}{A}_3=\mathrm{0,}{A}_5=\mathrm{0,...}\\ A_0=\frac{q}{4\pi {\epsilon }_{0}a}{P}_0(0),A_2=\frac{q}{4\pi {\epsilon }_{0}a}\frac{P_2(0)}{a^2}\mathrm{,...,}{A}_{2n}=\frac{q}{4\pi {\epsilon }_{0}a}\frac{P_{2n}(0)}{a^{2n}}\mathrm{,...}\end{array}\end{array}}$

La solución de la ecuación de Laplace para cualquier punto P (r,θ) con r<a es

${\displaystyle V_{r<a}(r,\theta )=\frac{q}{4\pi {\epsilon }_{0}a}\left\{P_0(\cos \theta )+P_2(0){\left(\frac{r}{a}\right)}^2{P}_2(\cos \theta )+P_4(0){\left(\frac{r}{a}\right)}^4{P}_4(\cos \theta )+\mathrm{....}{P}_{2n}(0){\left(\frac{r}{a}\right)}^{2n}{P}_{2n}(\cos \theta )+\mathrm{...}\right\}}$

Puntos P que distan r>a del centro del anillo

Para estos puntos el coeficiente A_n=0, para evitar que el potencial se haga infinito cuando r→∞

${\displaystyle V_{r>a}(r,\theta )={\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{r^{n+1}}{P}_n(\cos \theta )}}$

Escribimos el potencial en un punto del eje del anillo de la forma

${\displaystyle V(r\mathrm{,0})=\frac{1}{4\pi {\epsilon }_0}\frac{q}{\sqrt{a^2+r^2}}=\frac{q}{4\pi {\epsilon }_{0}r}\frac{1}{\sqrt{\frac{a^2}{r^2}+1}}}$

Desarrollamos en serie (1+x²)^-1/2 y calculamos los coeficientes B_n comparando el potencial en un punto del eje del anillo, V(r, 0) con la solución de la ecuación de Laplace para los puntos del eje del anillo θ=0

${\displaystyle {\left(1+{\left(\frac{a}{r}\right)}^2\right)}^{-1/2}=1-\frac{1}{2}{\left(\frac{a}{r}\right)}^2+\frac{3}{8}{\left(\frac{a}{r}\right)}^4-\frac{5}{16}{\left(\frac{a}{r}\right)}^6+\mathrm{...}{\left(-1\right)}^m\frac{(2m)!}{2^{m}m!·2^{m}m!}{\left(\frac{a}{r}\right)}^{2m}+\mathrm{...}}$

La solución de la ecuación de Laplace para cualquier punto P (r,θ) con r>a es

${\displaystyle V_{r>a}(r,\theta )=\frac{q}{4\pi {\epsilon }_{0}r}\left\{P_0(\cos \theta )+P_2(0){\left(\frac{a}{r}\right)}^2{P}_2(\cos \theta )+P_4(0){\left(\frac{a}{r}\right)}^4{P}_4(\cos \theta )+\mathrm{....}{P}_{2n}(0){\left(\frac{a}{r}\right)}^{2n}{P}_{2n}(\cos \theta )+\mathrm{...}\right\}}$

Ambas soluciones coinciden para r=a

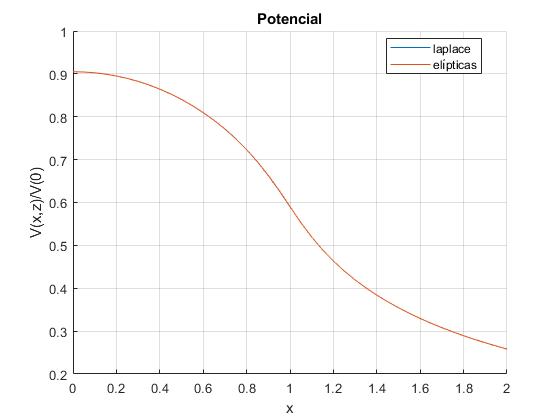
Sea un anillo de radio a=1. Representamos el potencial, en unidades del potencial en el centro del anillo V(0,0)=q/(4πε₀a), en la dirección radial de los puntos del plano paralelo al anillo y distante z=0.1. Comparamos esta representación gráfica con la que obtuvimos en la página titulada Campo y potencial eléctrico fuera del eje en términos de integrales elípticas

a=1; %radio del anillo
z=0.1; %por encima del plano del anillo
n=0:50; %número de términos del desarrollo en serie
xx=0:0.05:2;
V=zeros(1,length(xx));
i=0;
for x=xx
    r=sqrt(x^2+z^2);
    ch=cos(atan(x/z));
    i=i+1;
    if r<a
       V(i)=sum(legendreP(2*n,0).*legendreP(2*n,ch).*(r/a).^(2*n)); 
    else
       V(i)=a*sum(legendreP(2*n,0).*legendreP(2*n,ch).*(a/r).^(2*n))/r;       
    end
end
hold on
plot(xx,V);

%en términos de integrales elípticas
m=@(x) 4*a*x./(z.^2+(x+a).^2);
V=@(x) 2*a*ellipke(m(x))./sqrt(z.^2+(x+a).^2)/pi;
fplot(V,[0,2])

hold off
grid on
xlabel('x')
legend('legendre','elíptica','location','best')
ylabel('V(x,z)/V(0)')
title('Potencial')

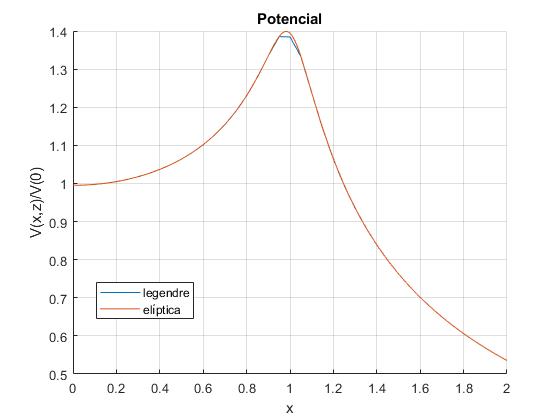
Observamos una pequeña discrepancia para puntos situados encima del anillo, r≈a

Se sugiere al lector cambiar el valor de la variable z=0.25, 0.5, 1. Observar el efecto del número de términos del desarrollo en serie, en esta representación gráfica, se han tomado n=50, probar con 10, etc.

Potencial de un disco

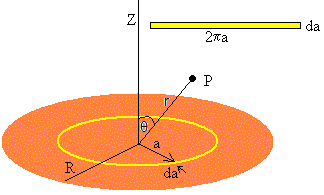
El potencial producido por un disco de radio R uniformente cargado con una carga Q en un punto P, es la suma de los potenciales producidos en P por los anillos concéntricos de carga dq de radio a y anchura da

La carga dq de un anillo de radio a es

${\displaystyle dq=\frac{Q}{\pi R^2}2\pi a·da=2\frac{Q}{R^2}a·da}$

En las dos expresiones del potencial producido por un anillo cargado, sustituimos la carga q por la carga dq

${\displaystyle \begin{array}{l}d{V}_{r<a}(r,\theta )=\frac{Q}{2\pi {\epsilon }_0{R}^2}da\left\{P_0(\cos \theta )+P_2(0){\left(\frac{r}{a}\right)}^2{P}_2(\cos \theta )+P_4(0){\left(\frac{r}{a}\right)}^4{P}_4(\cos \theta )+\mathrm{....}{P}_{2n}(0){\left(\frac{r}{a}\right)}^{2n}{P}_{2n}(\cos \theta )+\mathrm{...}\right\}\\ d{V}_{r>a}(r,\theta )=\frac{Q}{2\pi {\epsilon }_0{R}^2}\frac{a}{r}da\left\{P_0(\cos \theta )+P_2(0){\left(\frac{a}{r}\right)}^2{P}_2(\cos \theta )+P_4(0){\left(\frac{a}{r}\right)}^4{P}_4(\cos \theta )+\mathrm{....}{P}_{2n}(0){\left(\frac{a}{r}\right)}^{2n}{P}_{2n}(\cos \theta )+\mathrm{...}\right\}\end{array}}$

Puntos P que distan r>R del centro del disco

Para todos los anillos que componen el disco cargado se cumple la condición r>a.

${\displaystyle \begin{array}{l}{V}_{r>R}(r,\theta )=\frac{Q}{2\pi {\epsilon }_0{R}^2}\frac{1}{r}{\displaystyle \underset{0}{\overset{R}{\int }}\left\{P_0(\cos \theta )+P_2(0){\left(\frac{a}{r}\right)}^2{P}_2(\cos \theta )+P_4(0){\left(\frac{a}{r}\right)}^4{P}_4(\cos \theta )+\mathrm{....}{P}_{2n}(0){\left(\frac{a}{r}\right)}^{2n}{P}_{2n}(\cos \theta )+\mathrm{...}\right\}a·da}=\\ \frac{Q}{2\pi {\epsilon }_0{R}^2}\frac{1}{r}\left\{P_0(\cos \theta )\frac{R^2}{2}+P_2(0)\frac{1}{r^2}\frac{R^4}{4}{P}_2(\cos \theta )+P_4(0)\frac{1}{r^4}\frac{R^6}{6}{P}_4(\cos \theta )+\mathrm{....}{P}_{2n}(0)\frac{1}{r^{2n}}\frac{R^{2n+2}}{2n+2}{P}_{2n}(\cos \theta )+\mathrm{...}\right\}=\\ \frac{Q}{2\pi {\epsilon }_0}\frac{1}{r}\left\{\frac{1}{2}{P}_0(\cos \theta )+\frac{1}{4}{P}_2(0){\left(\frac{R}{r}\right)}^2{P}_2(\cos \theta )+\frac{1}{6}{P}_4(0){\left(\frac{R}{r}\right)}^4{P}_4(\cos \theta )+\mathrm{....}\frac{1}{2n+2}{P}_{2n}(0){\left(\frac{R}{r}\right)}^{2n}{P}_{2n}(\cos \theta )+\mathrm{...}\right\}\end{array}}$

El resultado es

${\displaystyle V_{r>R}(r,\theta )=\frac{Q}{2\pi {\epsilon }_{0}R}{\displaystyle \sum _{n=0}^{\infty }\frac{1}{2n+2}}{\left(\frac{R}{r}\right)}^{2n+1}{P}_{2n}(0)P_{2n}(\cos \theta )}$

Puntos P que distan r<R del centro del disco

El potencial en P es la suma de dos potenciales, la producida por

• Los anillos de radio a<r, integral de dV_r>a(r,θ)
• Los anillos de radio a>r, integral de dV_r<a(r,θ)

${\displaystyle \begin{array}{l}{V}_{r<R}(r,\theta )=\frac{Q}{2\pi {\epsilon }_0{R}^2}\frac{1}{r}{\displaystyle \underset{0}{\overset{r}{\int }}\left\{P_0(\cos \theta )+P_2(0){\left(\frac{a}{r}\right)}^2{P}_2(\cos \theta )+P_4(0){\left(\frac{a}{r}\right)}^4{P}_4(\cos \theta )+\mathrm{....}{P}_{2n}(0){\left(\frac{a}{r}\right)}^{2n}{P}_{2n}(\cos \theta )+\mathrm{...}\right\}a·da}+\\ \frac{Q}{2\pi {\epsilon }_0{R}^2}{\displaystyle \underset{r}{\overset{R}{\int }}\left\{P_0(\cos \theta )+P_2(0){\left(\frac{r}{a}\right)}^2{P}_2(\cos \theta )+P_4(0){\left(\frac{r}{a}\right)}^4{P}_4(\cos \theta )+\mathrm{....}{P}_{2n}(0){\left(\frac{r}{a}\right)}^{2n}{P}_{2n}(\cos \theta )+\mathrm{...}\right\}da}=\\ \frac{Q}{2\pi {\epsilon }_{0}R}\frac{r}{R}\left\{\frac{1}{2}{P}_0(\cos \theta )+\frac{1}{4}{P}_2(0)P_2(\cos \theta )+\frac{1}{6}{P}_4(0)P_4(\cos \theta )+\mathrm{....}\frac{1}{2n+2}{P}_{2n}(0)P_{2n}(\cos \theta )+\mathrm{...}\right\}+\\ \frac{Q}{2\pi {\epsilon }_0{R}^2}\left\{P_0(\cos \theta )\left(R-r\right)+P_2(0)\left(\frac{1}{r}-\frac{1}{R}\right)r^2{P}_2(\cos \theta )+P_4(0)\frac{1}{3}\left(\frac{1}{r^3}-\frac{1}{R^3}\right)r^4{P}_4(\cos \theta )+\mathrm{....}{P}_{2n}(0)\frac{1}{2n-1}\left(\frac{1}{r^{2n-1}}-\frac{1}{R^{2n-1}}\right)r^{2n}{P}_{2n}(\cos \theta )+\mathrm{...}\right\}=\\ \frac{Q}{2\pi {\epsilon }_{0}R}\frac{r}{R}\left\{\frac{1}{2}{P}_0(\cos \theta )+\frac{1}{4}{P}_2(0)P_2(\cos \theta )+\frac{1}{6}{P}_4(0)P_4(\cos \theta )+\mathrm{....}\frac{1}{2n+2}{P}_{2n}(0)P_{2n}(\cos \theta )+\mathrm{...}\right\}+\\ \frac{Q}{2\pi {\epsilon }_{0}R}\frac{r}{R}\left\{-P_0(\cos \theta )+P_2(0)P_2(\cos \theta )+P_4(0)\frac{1}{3}{P}_4(\cos \theta )+\mathrm{....}{P}_{2n}(0)\frac{1}{2n-1}{P}_{2n}(\cos \theta )+\mathrm{...}\right\}\\ -\frac{Q}{2\pi {\epsilon }_{0}R}\left\{-P_0(\cos \theta )\frac{r}{R}+P_2(0)\frac{r^2}{R^2}{P}_2(\cos \theta )+P_4(0)\frac{1}{3}\frac{r^4}{R^4}{P}_4(\cos \theta )+\mathrm{....}{P}_{2n}(0)\frac{1}{2n-1}\frac{r^{2n}}{R^{2n}}{P}_{2n}(\cos \theta )+\mathrm{...}\right\}\end{array}}$

El resultado es

${\displaystyle V_{r<R}(r,\theta )=\frac{Q}{2\pi {\epsilon }_{0}R}\frac{r}{R}{\displaystyle \sum _{n=0}^{\infty }\left(\frac{1}{2n+2}+\frac{1}{2n-1}\right)}{P}_{2n}(0)P_{2n}(\cos \theta )-\frac{Q}{2\pi {\epsilon }_{0}R}{\displaystyle \sum _{n=0}^{\infty }\frac{1}{2n-1}{\left(\frac{r}{R}\right)}^{2n}{P}_{2n}(0)P_{2n}(\cos \theta )}}$

El potencial en la superficie del disco θ=π/2 es

${\displaystyle V_{r<R}\left(r,\frac{\pi }{2}\right)=\frac{Q}{2\pi {\epsilon }_{0}R}\frac{r}{R}{\displaystyle \sum _{n=0}^{\infty }\left(\frac{1}{2n+2}+\frac{1}{2n-1}\right)}{P}_{2n}^2(0)-\frac{Q}{2\pi {\epsilon }_{0}R}{\displaystyle \sum _{n=0}^{\infty }\frac{1}{2n-1}\frac{r^{2n}}{R^{2n}}{P}_{2n}^2(0)}}$

Calculamos el potencial en el centro del disco r=0, el primer término es nulo y en el segundo, el primer sumando n=0 de la serie es distinto de cero

${\displaystyle V\left(\mathrm{0,}\frac{\pi }{2}\right)=-\frac{Q}{2\pi {\epsilon }_{0}R}\frac{1}{-1}{P}_0^2(0)=\frac{Q}{2\pi {\epsilon }_{0}R}}$

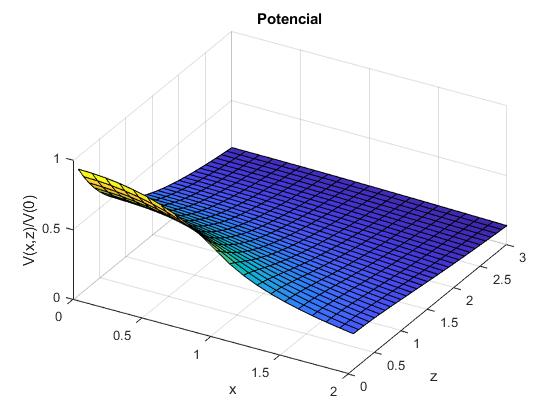
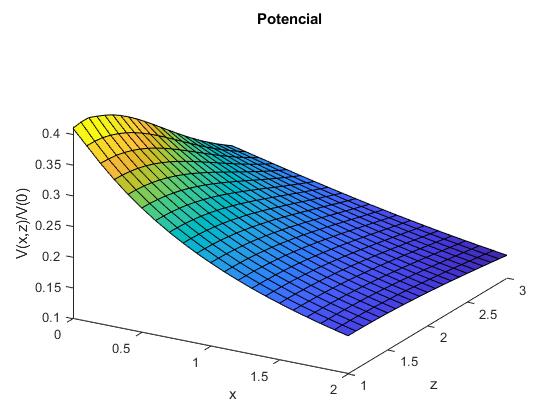
Representamos el potencial, en unidades del potencial en el centro del disco, de un disco de radio R=1 uniformemente cargado, en función de la distancia radial al eje y de la distancia z la plano del disco.

R=1; %radio del disco
xx=0:0.1:2;
zz=0.1:0.1:3;
V=zeros(length(zz),length(xx));
i=0; j=0;
n=0:20; %número de términos de la serie
for z=zz
    i=i+1;
    j=0;
    for x=xx
        j=j+1;
        r=sqrt(x^2+z^2);
        ch=cos(atan(x/z));
        if r<R
            V(i,j)=r*sum(legendreP(2*n,0).*legendreP(2*n,ch).
*(1./(2*n+2)+1./(2*n-1)))/R-sum(legendreP(2*n,0).*legendreP(2*n,ch).
*(r/R).^(2*n)./(2*n-1));
        else
            V(i,j)=sum(legendreP(2*n,0).*legendreP(2*n,ch).
*(R/r).^(2*n+1)./(2*n+2));       
        end
    end
end
[xx,zz]=meshgrid(xx,zz);
surf(xx,zz,V)
xlabel('x')
ylabel('z')
zlabel('V(x,z)/V(0)')
title('Potencial')
view(30,47)

Sea un disco de radio R=1. Representamos el potencial, en unidades del potencial en el centro del disco V(0,0)=Q/(4πε₀a), en la dirección radial de los puntos del plano paralelo al disco y distante z=0.1. Comparamos esta representación gráfica con la que obtuvimos en la página titulada Campo y potencial eléctrico fuera del eje en términos de integrales elípticas

function disco_1()
R=1; %radio del disco
n=0:50; %número de términos de la serie
z=0.1; %por encima del plano del disco
hold on

xx=0:0.05:2;
V=zeros(1,length(xx));
i=0;
for x=xx
    r=sqrt(x^2+z^2);
    ch=cos(atan(x/z));
    i=i+1;
    if r<R
        V(i)=r*sum(legendreP(2*n,0).*legendreP(2*n,ch).*
(1./(2*n+2)+1./(2*n-1)))/R-sum(legendreP(2*n,0).*
legendreP(2*n,ch).*(r/R).^(2*n)./(2*n-1));
    else
        V(i)=sum(legendreP(2*n,0).*legendreP(2*n,ch).*
(R/r).^(2*n+1)./(2*n+2));       
    end
end
plot(xx,V)

%funciones elípticas
V=zeros(1,length(xx));
i=1;
for x=xx
    V(i)=2*integral(@ potencial, 0,R)/(pi*R);
    i=i+1;
end
plot(xx,V)

hold off
grid on
xlabel('x')
legend('laplace','elípticas','location','best')
ylabel('V(x,z)/V(0)')
title('Potencial')

  
function res=potencial(a)
        m=4*a.*x./(z^2+(x+a).^2);
        res=a.*ellipke(m)./sqrt(z^2+(x+a).^2);
    end
end

Se sugiere al lector cambiar el valor de la variable z=0.25, 0.5, 1. Observar el efecto del número de términos del desarrollo en serie, en esta representación gráfica, se han tomado n=50, probar con 10, etc.

Ecuación de Laplace para el disco, r>R

En este apartado, buscamos la solución alternativa de la ecuación de Laplace en coordenadas esféricas para los puntos r>R

${\displaystyle V(r,\theta )={\displaystyle \sum _{n=0}^{\infty }\left(A_n{r}^n+\frac{B_n}{r^{n+1}}\right)}{P}_n(\cos \theta )}$

Como V→0 cuando r→∞, A_n=0 en la región del espacio r>R que rodea al disco

${\displaystyle V(r,\theta )={\displaystyle \sum _{n=0}^{\infty }\frac{B_n}{r^{n+1}}{P}_n(\cos \theta )}}$

Puntos por encima del plano del disco, z>0

En la página previa hemos calculado el potencial producido por un disco cargado en un punto de su eje, θ=0 (z>0), r=z, lo que nos permite calcular los coeficientes B_n, sabiendo que para θ=0, cos θ=1, los polinomios de Legendre, P_n(1)=1.

${\displaystyle \begin{array}{l}V(r\mathrm{,0})={\displaystyle \sum _{n=0}^{\infty }{B}_n{\left(\frac{R}{r}\right)}^{n+1}}=\frac{\sigma }{2{\epsilon }_0}\left(\sqrt{R^2+r^2}-r\right)\\ V(r\mathrm{,0})={\displaystyle \sum _{n=0}^{\infty }{B}_n{\left(\frac{R}{r}\right)}^{n+1}}=\frac{\sigma }{2{\epsilon }_0}r\left(\sqrt{{\left(\frac{R}{r}\right)}^2+1}-1\right)\end{array}}$

Desarrollamos en serie el miembro derecho

>> syms x;
>> taylor(sqrt(1+x^2),x, 0,'Order',12)
ans =(7*x^10)/256 - (5*x^8)/128 + x^6/16 - x^4/8 + x^2/2 + 1

${\displaystyle \begin{array}{l}{\displaystyle \sum _{n=0}^{\infty }{B}_n}{x}^{n+1}=\frac{\sigma R}{2{\epsilon }_0}\frac{1}{x}\left(\sqrt{x^2+1}-1\right)\\ B_{0}x+B_1{x}^2+B_2{x}^3+B_3{x}^4+B_4{x}^5+B_5{x}^6+B_6{x}^7+B_7{x}^8+B_8{x}^9+B_9{x}^{10}+\mathrm{..}\approx \\ \frac{\sigma R}{2{\epsilon }_0}\left(\frac{x}{2}-\frac{x^3}{8}+\frac{x^5}{16}-\frac{5x^7}{128}+\frac{7x^9}{256}\mathrm{...}\right)\\ B_{2n-1}=0\\ B_{2n-2}=\frac{\sigma R}{2{\epsilon }_0}\frac{\frac{1}{2}\left(\frac{1}{2}-1\right)\mathrm{....}\left(\frac{1}{2}-n+1\right)}{n!}\end{array}}$

Por ejemplo, el coeficiente B₆ es proporcional a -5/128. B₆=B_2·4-2, n=4

>> n=4;
>> j=1:n;
>> prod(1/2-j+1)/factorial(n)
ans =   -0.0391
>> -5/128
ans =    -0.0391

Por ejemplo, el coeficiente B₈ es proporcional a 7/256. B₈=B_2·5-2, n=5

>> n=5;
>> j=1:n;
>> prod(1/2-j+1)/factorial(n)
ans =    0.0273
>> 7/256
ans =    0.0273

El potencial en un punto (r,θ), tal que r>R por encima del disco z>0, es

${\displaystyle V(r,\theta )=\frac{\sigma R}{2{\epsilon }_0}{\displaystyle \sum _{n=1}^{\infty }\frac{\frac{1}{2}\left(\frac{1}{2}-1\right)\mathrm{....}\left(\frac{1}{2}-n+1\right)}{n!}{\left(\frac{R}{r}\right)}^{2n-1}}{P}_{2n-2}(\cos \theta )}$

Puntos por debajo del plano del disco, z<0

En la página previa hemos calculado el potencial producido por un disco cargado en un punto de su eje, lo que nos permite calcular los coeficientes B_n, sabiendo que para θ=π (z<0), r=|z|, cos θ=-1, los polinomios de Legendre, P_n(-1)=(-1)ⁿ.

${\displaystyle \begin{array}{l}V(r\mathrm{,}\pi )={\displaystyle \sum _{n=0}^{\infty }{B}_n{\left(\frac{R}{r}\right)}^{n+1}}{\left(-1\right)}^n=\frac{\sigma }{2{\epsilon }_0}\left(\sqrt{R^2+r^2}-r\right)\\ V(r\mathrm{,}\pi )={\displaystyle \sum _{n=0}^{\infty }{B}_n{\left(\frac{R}{r}\right)}^{n+1}}{\left(-1\right)}^n=\frac{\sigma }{2{\epsilon }_0}r\left(\sqrt{{\left(\frac{R}{r}\right)}^2+1}-1\right)\end{array}}$

Los coeficientes B_n valen

${\displaystyle \begin{array}{l}{\displaystyle \sum _{n=0}^{\infty }{B}_n{\left(\frac{R}{r}\right)}^{n+1}{\left(-1\right)}^n}=\frac{\sigma R}{2{\epsilon }_0}\frac{r}{R}\left(\sqrt{{\left(\frac{R}{r}\right)}^2+1}-1\right)\\ {\displaystyle \sum _{n=0}^{\infty }{B}_n}{x}^{n+1}{\left(-1\right)}^n=\frac{\sigma R}{2{\epsilon }_0}\frac{1}{x}\left(\sqrt{x^2+1}-1\right)\\ B_{0}x-B_1{x}^2+B_2{x}^3-B_3{x}^4+B_4{x}^5-B_5{x}^6+B_6{x}^7-B_7{x}^8+B_8{x}^9-B_9{x}^{10}+\mathrm{..}\approx \\ \frac{\sigma R}{2{\epsilon }_0}\left(\frac{x}{2}-\frac{x^3}{8}+\frac{x^5}{16}-\frac{5x^7}{128}+\frac{7x^9}{256}\mathrm{...}\right)\\ B_{2n-1}=0\\ B_{2n-2}=\frac{\sigma R}{2{\epsilon }_0}\frac{\frac{1}{2}\left(\frac{1}{2}-1\right)\mathrm{....}\left(\frac{1}{2}-n+1\right)}{n!}\end{array}}$

Obtenemos el mismo resultado que para z>0, como cabría esperar

Representamos el potencial V(x,z) en unidades del potencial en el centro del disco V(0)=σR/(2ε₀) para los puntos r>R

R=1; %radio del disco
x=0:0.1:2;
z=1:0.1:3;  %r>R
V=zeros(length(x), length(z));
for i=1:length(x)
    for j=1:length(z)
        vp=0;
        X=0.1*(i-1);
        Z=1+(j-1)*0.1;
        th=atan2(X,Z);
        r=sqrt(X^2+Z^2);
        for n=1:10
            k=1:n;
            vp=vp+prod(1/2-k+1)*(R/r)^(2*n-1)*legendreP(2*n-2, cos(th))
/factorial(n);
        end
        V(i,j)=vp/R;
    end
end
hold on
[x,z]=meshgrid(x,z);
surf(x,z,V)
xlabel('x')
ylabel('z')
zlabel('V(x,z)/V(0)')
title('Potencial')
view(30,30)

Representamos el potencial V(x,z) en unidades del potencial en el centro del disco V(0)=σR/(2ε₀) para los puntos r>R, utilizando las dos soluciones de la ecuación de Laplace

R=1; %radio del disco
z=1.2; %por encima del plano del disco r>R
hold on

xx=0:0.05:2;
%primera solución de la ecuación de Laplace
V=zeros(1,length(xx));
i=0;
n=0:50; %número de términos de la serie
for x=xx
    r=sqrt(x^2+z^2);
    ch=cos(atan(x/z));
    i=i+1;
    if r<R
        V(i)=r*sum(legendreP(2*n,0).*legendreP(2*n,ch).*
(1./(2*n+2)+1./(2*n-1)))/R-sum(legendreP(2*n,0).*legendreP(2*n,ch).
*(r/R).^(2*n)./(2*n-1));
    else
        V(i)=sum(legendreP(2*n,0).*legendreP(2*n,ch).*
(R/r).^(2*n+1)./(2*n+2));       
    end
end
plot(xx,V)

%segunda solución de la ecuación de Laplace
V=zeros(1,length(xx));
i=0;
for x=xx
    r=sqrt(x^2+z^2);
    ch=cos(atan(x/z));
    i=i+1;
    vp=0;
    for n=1:10
       k=1:n;
       vp=vp+prod(1/2-k+1)*(R/r)^(2*n-1)*legendreP(2*n-2, ch)
/factorial(n);
     end
     V(i)=vp/R;
end
plot(xx,V)

hold off
grid on
xlabel('x')
legend('laplace 1','laplace 2','location','best')
ylabel('V(x,z)/V(0)')
title('Potencial')

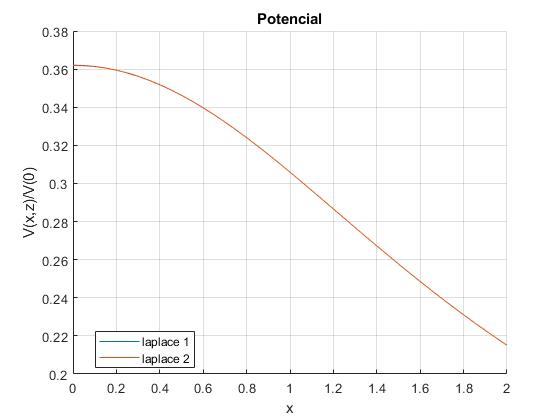
Observamos que ambas soluciones de la ecuación de Laplace para el disco coinciden

Campo eléctrico, para los puntos r>R

${\displaystyle \overrightarrow{E}=-\frac{\partial V(r,\theta )}{\partial r}\widehat{r}-\frac{1}{r}\frac{\partial V(r,\theta )}{\partial \theta }\widehat{\theta }}$

Las componentes del campo eléctrico

${\displaystyle \begin{array}{l}{E}_r(r,\theta )=\frac{\sigma }{2{\epsilon }_0}{\displaystyle \sum _{n=1}^{\infty }\frac{\frac{1}{2}\left(\frac{1}{2}-1\right)\mathrm{....}\left(\frac{1}{2}-n+1\right)}{n!}(2n-1){\left(\frac{R}{r}\right)}^{2n}}{P}_{2n-2}(\cos \theta )\\ E_{\theta }(r,\theta )=\frac{\sigma }{2{\epsilon }_0}{\displaystyle \sum _{n=1}^{\infty }\frac{\frac{1}{2}\left(\frac{1}{2}-1\right)\mathrm{....}\left(\frac{1}{2}-n+1\right)}{n!}{\left(\frac{R}{r}\right)}^{2n}}\sin (\theta ){\frac{d{P}_{2n-2}(x)}{dx}|}_{x=\cos \theta }\end{array}}$

Utilizamos la propiedad de los polinomios de Legendre P_n(x) para calcular su derivada respecto de x=cosθ

${\displaystyle \begin{array}{l}\frac{d{P}_{n+1}(x)}{dx}=(n+1)P_n(x)+x\frac{d{P}_n(x)}{dx}\\ \frac{d{P}_0(x)}{dx}=\mathrm{0,}\frac{d{P}_1(x)}{dx}=\mathrm{1,}\frac{d{P}_2(x)}{dx}=3x\mathrm{,....}\end{array}}$

Las componentes rectangulares del campo eléctrico

${\displaystyle \begin{array}{l}{E}_x=E_r\sin \theta +E_{\theta }\cos \theta \\ E_z=E_r\cos \theta -E_{\theta }\sin \theta \end{array}}$

R=1; %radio del disco
hold on
X=linspace(0,2,100);
Ez=zeros(1,length(X));
Ex=zeros(1,length(X));
z=1.5;%mayor que R
i=1;
for x=X
    th=atan2(x,z);
    r=sqrt(x^2+z^2);
    Er=0;
    Et=0;
    Dp=0;    
    for n=1:10
        k=1:n;
        Er=Er+prod(1/2-k+1)*(R/r)^(2*n)*(2*n-1)*legendreP(2*n-2, cos(th))
/factorial(n);
        Et=Et+prod(1/2-k+1)*(R/r)^(2*n)*sin(th)*Dp/factorial(n);
        Dp1=(2*n-1)*legendreP(2*n-2, cos(th))+cos(th)*Dp;
        Dp=2*n*legendreP(2*n-1, cos(th))+cos(th)*Dp1;
    end
    Ex(i)=(Er*sin(th)+Et*cos(th))*pi;
    Ez(i)=(Er*cos(th)-Et*sin(th))*pi;
    i=i+1;
end
plot(X, Ex)
plot(X,Ez)
hold off
grid on
xlabel('x')
ylabel('E_x, E_z')
legend('E_x','E_z')
title('Componentes, E_x, E_z')   

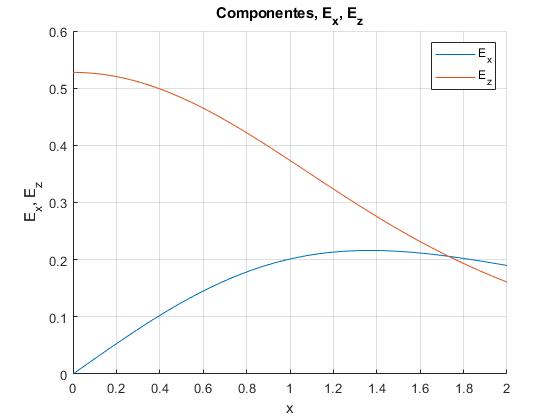
Obtenemos una representación similar a la obtenida utilizando funciones elípticas. Cabe resaltar el considerable tiempo de cálculo que le lleva a MATLAB, tomando 2n=20 términos de la serie

Referencias

Tingting Liu, Haibin Sun. Electric Potential of a Uniform Charged Disc in Whole by Method of Superposition. Applied Physics Research, Vol. 2, No. 1, May 2010, ISSN: 1916-9639

Lim Yung-kuo. Problems and Solutions on Electromagnetism. World Scientific (1993). Problem 1009, pp. 11-14