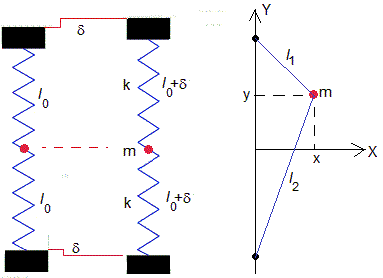
Sea una partícula de masa m unida a dos muelles elásticos iguales de constante k, supondremos que están en el plano horizontal y la partícula desliza en este plano sin rozamiento alguno. l₀ es la longitud de los muelles sin deformar, cuando la separación entre los extremos de los muelles es 2l₀.

Separamos los extremos de los muelles 2(l₀+δ) y desplazamos la partícula al punto de coordendas (x,y)

La energía potencial elástica del sistema formado por los dos muelles iguales es

${\displaystyle \begin{array}{l}U(x,y)=\frac{1}{2}k{\left(l_1-l_0\right)}^2+\frac{1}{2}k{\left(l_2-l_0\right)}^2\\ l_1^2={\left(l_0+\delta -y\right)}^2+x^2\\ l_2^2={\left(l_0+\delta +y\right)}^2+x^2\end{array}}$

Las ecuaciones del movimiento de la partícula son

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-\frac{\partial U}{\partial x}\\ m\frac{d^{2}y}{d{t}^2}=-\frac{\partial U}{\partial y}\\ m\frac{d^{2}x}{d{t}^2}=-2kx+kx\left(\frac{l_0}{\sqrt{{\left(l_0+\delta -y\right)}^2+x^2}}+\frac{l_0}{\sqrt{{\left(l_0+\delta +y\right)}^2+x^2}}\right)\\ m\frac{d^{2}y}{d{t}^2}=-2ky+k{l}_0\left(\frac{l_0+\delta +y}{\sqrt{{\left(l_0+\delta +y\right)}^2+x^2}}-\frac{l_0+\delta -y}{\sqrt{{\left(l_0+\delta -y\right)}^2+x^2}}\right)\end{array}}$

En principio, δ podría ser positivo o negativo. En el caso de que fuese negativo, la partícula estaría en un estado inestable en el origen, por tanto, no vamos a tratar este caso. Consideraremos solamente el caso δ≥0.

Dada la posición inicial y la velocidad inicial de la partícula, se resuelve el sistema de dos ecuaciones diferenciales por procedimientos numéricos.

Casos particulares:

• Vibración a lo largo del eje Y, x=0

${\displaystyle m\frac{d^{2}y}{d{t}^2}=-2ky}$

La partícula describe un Movimiento Armónico Simple, que la se ha estudiado

• Vibración a lo largo del eje X, y=0

${\displaystyle m\frac{d^{2}x}{d{t}^2}=-2kx+2kx\frac{l_0}{\sqrt{{\left(l_0+\delta \right)}^2+x^2}}}$

Supongamos que el desplazamiento x de la partícula es mucho más pequeño que l₀+δ

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-2kx+2kx\frac{l_0}{l_0+\delta }{\left(1+\frac{x^2}{{\left(l_0+\delta \right)}^2}\right)}^{-1/2}\approx -2kx+2kx\frac{l_0}{l_0+\delta }\left(1-\frac{1}{2}\frac{x^2}{{\left(l_0+\delta \right)}^2}\right)\\ m\frac{d^{2}x}{d{t}^2}\approx -2k\left(\frac{\delta }{l_0+\delta }\right)x-k\frac{l_0}{{\left(l_0+\delta \right)}^3}{x}^3\end{array}}$

En esta página, estudiamos lasoscilaciones de la partícula a lo largo del eje X, que son no armónicas, incluso cuando el desplazamiento x es pequeño

Para encontrar la ecuación del movimiento de la partícula a lo largo del eje X, empezaremos por el caso más simple, δ=0, la ecuación del movimiento se reduce a

${\displaystyle \frac{d^{2}x}{d{t}^2}\approx -\frac{k}{m{l}_0^2}{x}^3}$

Oscilaciones a lo largo del eje X, δ=0

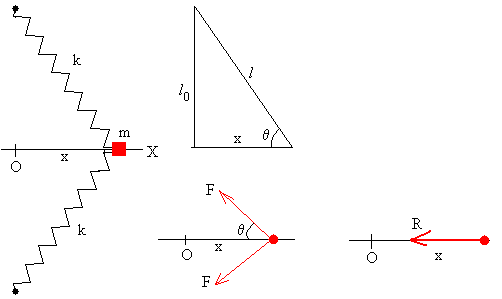
Sea un bloque de masa m unido a dos muelles elásticos iguales de constante k. La longitud de los muelles si deformar es l₀, cuando el sistema está en la posición de equilibrio estable x=0.

Cuando se separa el bloque una distancia x de la posición de equilibrio y se suelta, empieza a oscilar con un periodo P.

La fuerza F que ejerce cada uno de los muelles sobre el bloque es

${\displaystyle F=k\left(\sqrt{x^2+l_0^2}-l_0\right)}$

La resultante es

${\displaystyle R=2F\cos \theta =2F\frac{x}{\sqrt{x^2+l_0^2}}=2k\left(1-\frac{l_0}{\sqrt{x^2+l_0^2}}\right)x}$

Energía potencial

La resultante es una fuerza conservativa, su energía potencial E_p(x) es

${\displaystyle \begin{array}{l}-2k\left(1-\frac{l_0}{\sqrt{x^2+l_0^2}}\right)x=-\frac{d{E}_p(x)}{dx}\\ E_p(x)={\displaystyle \int 2k\left(1-\frac{l_0}{\sqrt{x^2+l_0^2}}\right)x·dx+c}\end{array}}$

Elegimos la constante aditiva c de modo que cuando x=0, (muelles sin deformar) E_p(0)=0

${\displaystyle E_p(x)=k{x}^2-2k{l}_0\sqrt{x^2+l_0^2}+2k{l}_0^2}$

Dada la energía total (cinética más potencial) E, la partícula se puede mover entre -A y +A, siendo A la amplitud, la raíz positiva de la ecuación bicuadrada

${\displaystyle \begin{array}{l}E=E_p(x)\\ E=k{x}^2-2k{l}_0\sqrt{x^2+l_0^2}+2k{l}_0^2\\ x^4-2\frac{E}{k}{x}^2+{\left(\frac{E}{k}\right)}^2-4\frac{E}{k}{l}_0^2=0\end{array}}$

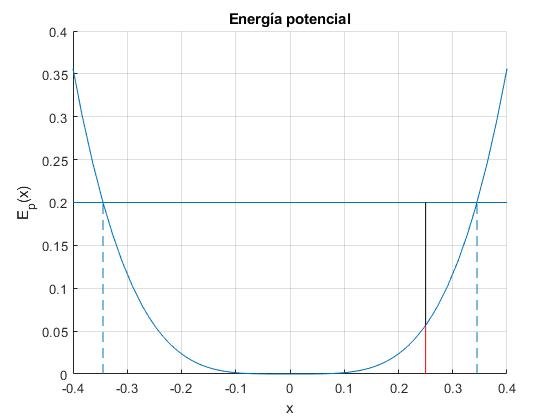
Representamos, la energía potencial, E_p(x) para k=60 N/m y l₀=1. La energía total E=0.2, se representa como una recta horizontal. Sus extremos son la amplitud ±A. Para x=0.25 m, el segmento vertical rojo, representa la energía potencial y el negro la energía cinética

k=60; %cociente k/m
l0=1; %longitud del muelle sin deformar
Ep=@(x) k*(x.^2-2*l0*sqrt(l0^2+x.^2))+2*k*l0^2;
hold on
fplot(Ep,[-0.4,0.4])
E=0.2;%0.1163;
b=-2*E/k;
c=(E/k)^2-4*E*l0^2/k;
x1=sqrt((-b+sqrt(b^2-4*c))/2); %amplitud
line([-0.4,0.4],[E,E]) %energía total
line([-x1,-x1],[0,E],'lineStyle','--')
line([x1,x1],[0,E],'lineStyle','--')
x=0.25;
line([x,x],[0,Ep(x)],'color','r') %energía potencial
line([x,x],[Ep(x),E],'color','k') %energía cinética
hold off
grid on
xlabel('x')
ylabel('E_p(x)')
title('Energía potencial')

Ecuación del movimiento

La ecuación del movimiento es

${\displaystyle m\frac{d^{2}x}{d{t}^2}=-2k\left(1-\frac{l_0}{\sqrt{x^2+l_0^2}}\right)x}$

Se transforma en

${\displaystyle \frac{d^{2}x}{d{t}^2}+\frac{2k}{m}x\left\{1-{\left(1+{\left(\frac{x}{l_0}\right)}^2\right)}^{-1/2}\right\}}$

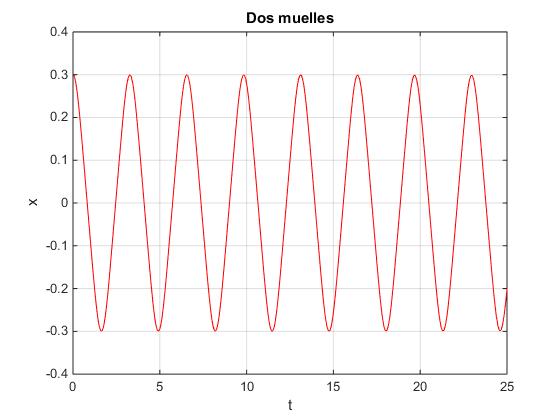
Esta ecuación, se resuelve aplicando procedimientos numéricos con las condiciones iniciales siguientes: en el instante inicial t=0, x=A, y v=dx/dt=0, siendo A la amplitud de la oscilación.

Utilizamos el procedimiento ode45 de MATLAB para resolver numéricamente la ecuación diferencial de segundo orden, para los valores de k/m=60, l₀=1 y una amplitud A=0.3

k=60; %cociente k/m
l0=1; %longitud del muelle sin deformar
f=@(t,x) [x(2);-2*k*x(1)*(1-1/sqrt(1+(x(1)/l0)^2))]; 
tspan=[0 25];
[t,x]=ode45(f,[0 25],[0.3,0]);
plot(t,x(:,1),'r')
grid on
xlabel('t')
ylabel('x');
title('Dos muelles')

Comprobamos que la energía por unidad de masa, permanece constante.

E=x(:,2).^2/2+k*(x(:,1).^2-2*l0*sqrt(l0^2+x(:,1).^2))+2*k*l0^2
    E =
    0.1163
    0.1163
    ....
    0.1147
    0.1147

Solución analítica

Cuando x<<l₀ la ecuación diferencial se aproxima a

${\displaystyle \frac{d^{2}x}{d{t}^2}+\frac{k}{m{l}_0^2}{x}^3=0}$

Las condiciones iniciales son: en el instante t=0, la partícula parte de la posición x=A, con velocidad nula, v=dx/dt=0

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=\frac{dv}{dt}=\frac{dv}{dx}·\frac{dx}{dt}=v\frac{dv}{dx}\\ v\frac{dv}{dx}=-\frac{k}{m{l}_0^2}{x}^3\end{array}}$

Integramos esta ecuación diferencial

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{v}{\int }}vdv}=-\frac{k}{m{l}_0^2}{\displaystyle \underset{A}{\overset{x}{\int }}{x}^{3}dx}\\ v=\sqrt{\frac{k}{2m{l}_0^2}(A^4-x^4)}\end{array}}$

es el módulo de la velocidad

Como la partícula parte de x=+A y se dirige hacia el origen la velocidad es negativa en el primer cuarto de periodo

${\displaystyle v=-\sqrt{\frac{k}{2m{l}_0^2}(A^4-x^4)}}$

Para obtener la posición x del oscilador en función del tiempo t tenemos que integrar nuevamente

${\displaystyle \begin{array}{l}\frac{dx}{dt}=-\sqrt{\frac{k}{2m{l}_0^2}(A^4-x^4)}\\ t=-\sqrt{\frac{2m{l}_0^2}{k}}{\displaystyle \underset{A}{\overset{x}{\int }}\frac{dx}{\sqrt{A^4-x^4}}}\end{array}}$

Hacemos el cambio de variable

${\displaystyle x=A\sqrt{1-z^2}}$

La integral se transforma

${\displaystyle \begin{array}{l}t=\frac{1}{A}\sqrt{\frac{2m{l}_0^2}{k}}{\displaystyle \underset{0}{\overset{z}{\int }}\frac{dz}{\sqrt{1-z^2}\sqrt{2-z^2}}}\\ \frac{A}{l_0}\sqrt{\frac{k}{m}}t={\displaystyle \underset{0}{\overset{z}{\int }}\frac{dz}{\sqrt{1-z^2}\sqrt{1-\frac{1}{2}{z}^2}}}\end{array}}$

Se hace el cambio de variable z=sinφ, obtenemos la integral elíptica F(θ, $\frac{1}{\sqrt{2}}$)

${\displaystyle \begin{array}{l}\frac{A}{l_0}\sqrt{\frac{k}{m}}t={\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{d\phi }{\sqrt{1-\frac{1}{2}{\sin }^2\phi }}}\\ \frac{A}{l_0}\sqrt{\frac{k}{m}}t=u\\ \text{sn}u=\sin \theta =z\end{array}}$

Las funciones sn y cn están relacionadas

sn²u+cn²u=1

Deshacemos el cambio de variable de z a x.

${\displaystyle \begin{array}{l}x=A\sqrt{1-z^2}=A\sqrt{1-{\text{sn}}^{2}u}=A\text{cn}u\hfill \\ x=A·\text{cn}\left(\frac{A}{l_0}\sqrt{\frac{k}{m}}t,\frac{1}{\sqrt{2}}\right)\hfill \end{array}}$

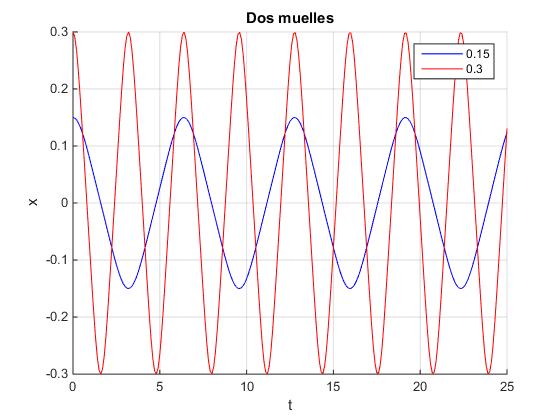
Tomando l₀=1, k/m=60, representamos el desplazamiento x del oscilador en función del tiempo t, para dos valores de la amplitud A=0.15 y A=0.3

k_m=sqrt(60);
A=0.15;
t=0:0.1:25;
[sn,cn,dn]=ellipj(A*k_m*t,1/2);
hold on
plot(t,cn*A,'b')
A=0.3;
[sn,cn,dn]=ellipj(A*k_m*t, 1/2);
plot(t,cn*A,'r')
hold off
xlabel('t')
ylabel('x')
legend ('0.15','0.3')
title('Dos muelles')
grid on

Periodo del movimiento

El tiempo que tarda en describir un cuarto de periodo P es

${\displaystyle \frac{P}{4}=-\sqrt{\frac{2m{l}_0^2}{k}}{\displaystyle \underset{A}{\overset{0}{\int }}\frac{dx}{\sqrt{A^4-x^4}}}}$

Haciendo el cambio de variable x=Acosφ

${\displaystyle \begin{array}{l}\frac{P}{4}=\frac{l_0}{A}\sqrt{\frac{m}{k}}\underset{0}{\overset{\pi /2}{{\displaystyle \int }}}\frac{d\phi }{\sqrt{1-\frac{1}{2}{\sin }^2\phi }}\\ \frac{P}{4}=\frac{l_0}{A}\sqrt{\frac{m}{k}}K\left(\frac{1}{\sqrt{2}}\right)\end{array}}$

El último término es la integral elíptica completa de primera especie. Su valor aproximado es 1.8541.

>> k2=1/2;
>> ellipke(k2)
ans =    1.8541

${\displaystyle P\approx 7.4164\frac{l_0}{A}\sqrt{\frac{m}{k}}}$

En la figura, se muestra cómo el periodo P depende de la amplitud A

• La curva en color rojo, la amplitud es A=0.3, el periodo es P=3.19 s
• La curva en color azul, la amplitud es A=0.15, el periodo es P=6.38 s

Oscilaciones a lo largo del eje X, δ≠0

La ecuación del movimiento de la particula a lo largo del eje X, con x<<(l₀+δ), es

${\displaystyle \frac{d^{2}x}{d{t}^2}=-Ax-B{x}^3\{\begin{array}{l}A=2\frac{k}{m}\left(\frac{\delta }{l_0+\delta }\right)\\ B=\frac{k}{m}\frac{l_0}{{\left(l_0+\delta \right)}^3}\end{array}}$

Las condiciones iniciales son: en el instante t=0, la partícula parte de la posición x=0 (origen), con velocidad, v=dx/dt=v₀

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=\frac{dv}{dt}=\frac{dv}{dx}·\frac{dx}{dt}=v\frac{dv}{dx}\hfill \\ v\frac{dv}{dx}=-Ax-B{x}^3\hfill \end{array}}$

Integramos esta ecuación diferencial

${\displaystyle \begin{array}{l}{\displaystyle \underset{v_0}{\overset{v}{\int }}vdv}=-{\displaystyle \underset{0}{\overset{x}{\int }}\left(Az+B{z}^3\right)dx}\\ {\left(\frac{dx}{dt}\right)}^2=\frac{1}{2}B\left(\frac{2v_0^2}{B}-\frac{2A}{B}{x}^2-x^4\right)\\ \sqrt{\frac{B}{2}}t={\displaystyle \underset{0}{\overset{x}{\int }}\frac{dz}{\sqrt{\frac{2v_0^2}{B}-\frac{2A}{B}{z}^2-z^4}}}\\ \sqrt{\frac{B}{2}}t={\displaystyle \underset{0}{\overset{x}{\int }}\frac{dz}{\sqrt{(a^2+z^2)(b^2-z^2)}}}\{\begin{array}{l}{b}^2=\sqrt{\frac{A^2}{B^2}+\frac{2v_0^2}{B}}-\frac{A}{B}\\ a^2=\sqrt{\frac{A^2}{B^2}+\frac{2v_0^2}{B}}+\frac{A}{B}\end{array}\end{array}}$

Buscamos en el libro titulado 'Table of Integrals, Series, and Products', la solución a integrales de este tipo y la encontramos en el apartado 3.152, n° 3 de la página 279

${\displaystyle {\displaystyle \underset{0}{\overset{x}{\int }}\frac{dz}{\sqrt{(z^2+a^2)(b^2-z^2)}}}=\frac{1}{\sqrt{a^2+b^2}}F\left(\gamma ,r\right)\{\begin{array}{l}\gamma =\arcsin \left(\frac{x}{b}\sqrt{\frac{a^2+b^2}{a^2+x^2}}\right)\\ r=\frac{b}{\sqrt{a^2+b^2}}\end{array},b\ge x>0}$

Despejamos la posición x en función del tiempo t, utilizando la función elíptica sn de Jacobi

${\displaystyle \begin{array}{l}\sqrt{B\frac{a^2+b^2}{2}}t=F\left(\gamma ,r\right)\\ \sin \gamma =\text{sn}\left(\sqrt{B\frac{a^2+b^2}{2}}t,r\right)\\ \frac{x}{b}\sqrt{\frac{a^2+b^2}{a^2+x^2}}=\text{sn}\left(\alpha t,r\right),\alpha =\sqrt{B\frac{a^2+b^2}{2}}\\ x=\frac{ab·\text{sn}\left(\alpha t,r\right)}{\sqrt{a^2+b^2{\text{cn}}^2\left(\alpha t,r\right)}}\end{array}}$

Se ha utilizado la relación

sn²u+cn²u=1

Periodo

En un Movimiento Armónico Simple, x=Asin(ωt+φ), es una función periódica de periodo P, tal que cuando se incrementa el tiempo t en P, la fase (argumento del seno) se incrementa en 2π

ω(t+P)+φ=ωt+φ+2π, P=2π/ω

Del mismo modo sn(αt,r) y cn(αt,r) son funciones periódicas que cuando el tiempo se incrementa en P, el argumento de se incrementa en 4K(r)

${\displaystyle \begin{array}{l}\alpha (t+P)=\alpha t+4K(r)\\ P=\frac{4K(r)}{\alpha }=\frac{8K(r)}{B\sqrt{a^2+b^2}}\end{array}}$

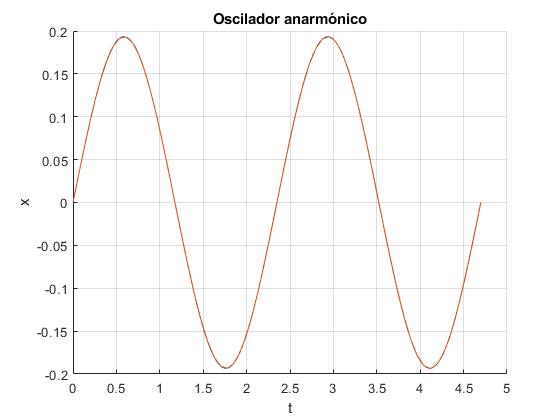
Representamos la posición x en función del tiempo t durante dos periodos, para δ=0.05, el cociente k/m=60, la longitud del muelle sin deformar l₀=1. La posición inicial x₀=0, y la velocidad inicial es v₀=0.5.

Comparamos la solución analítica y numérica, vemos que coinciden

k=60; %cociente k/m
l0=1; %longitud del muelle sin deformar
delta=0.05; %deformación inicial
v0=0.5; %velocidad inicial

A=2*k*delta/(l0+delta);
B=k*l0/(l0+delta)^3;
b2=-A/B+sqrt(A^2/B^2+2*v0^2/B);
a2=A/B+sqrt(A^2/B^2+2*v0^2/B);
r=sqrt(b2)/sqrt(a2+b2);
alfa=sqrt(B*(a2+b2)/2);
P=4*ellipke(r^2)/alfa; %periodo

t=linspace(0,2*P,200);
[sn,cn,dn]=ellipj(alfa*t,r^2);
x=sqrt(a2*b2)*sn./sqrt(a2+b2*cn.^2);
%procedimiento numérico
f=@(t,x) [x(2);-A*x(1)-B*x(1)^3]; 
[tt,xx]=ode45(f,[0,2*P],[0,v0]);
hold on
plot(t,x); %analítico
plot(tt,xx(:,1)) %numérico
hold off

grid on
xlabel('t')
ylabel('x');
title('Oscilador anarmónico')

Velocidad

Dada la posición x(t) respecto del tiempo, derivamos para calcular la velocidad, dx/dt. El lector puede consultar las fórmulas de la derivada de las funciones elípticas de Jacobi, sn(x) y cn(x)

${\displaystyle \begin{array}{l}v=\frac{dx}{dt}=ab\frac{\alpha ·\text{cn·dn}\sqrt{a^2+b^2{\text{cn}}^2}+\frac{b^2\alpha ·c\text{n·sn·dn}}{\sqrt{a^2+b^2{\text{cn}}^2}}}{a^2+b^2{\text{cn}}^2}=\\ \alpha ab·\frac{a^2+b^2}{{\left(a^2+b^2{\text{cn}}^2\left(\alpha t,r\right)\right)}^{3/2}}c\text{n}\left(\alpha t,r\right)\text{dn}\left(\alpha t,r\right)\end{array}}$

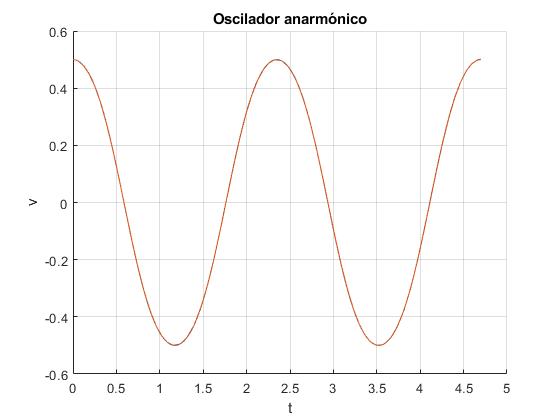
Representamos la posición v en función del tiempo t durante dos periodos, para δ=0.05, el cociente k/m=60, la longitud del muelle sin deformar l₀=1. La posición inicial x₀=0, y la velocidad inicial es v₀=0.5.

Comparamos la solución analítica y numérica, vemos que coinciden

k=60; %cociente k/m
l0=1; %longitud del muelle sin deformar
delta=0.05; %deformación inicial
v0=0.5; %velocidad inicial

A=2*k*delta/(l0+delta);
B=k*l0/(l0+delta)^3;
b2=-A/B+sqrt(A^2/B^2+2*v0^2/B);
a2=A/B+sqrt(A^2/B^2+2*v0^2/B);
r=sqrt(b2)/sqrt(a2+b2);
alfa=sqrt(B*(a2+b2)/2);
P=4*ellipke(r^2)/alfa;

t=linspace(0,2*P,200);
[sn,cn,dn]=ellipj(alfa*t,r^2);
v=alfa*sqrt(a2*b2)*(a2+b2)*cn.*dn./(a2+b2*cn.^2).^(3/2); %velocidad
%procedimiento numérico
f=@(t,x) [x(2);-A*x(1)-B*x(1)^3]; 
[tt,xx]=ode45(f,[0,2*P],[0,v0]);
hold on
plot(t,v); %analítico
plot(tt,xx(:,2)) %numérico
hold off

grid on
xlabel('t')
ylabel('v');
title('Oscilador anarmónico')  

Referencias

Detcheva V., Spassov V., A simple nonlinear oscillator: analytical and numerical solution. Phys. Educ. 28 (1993) pp. 39-42

I.S. Gradshteyn, I.M. Ryzhik. Table of Integrals, Series, and Products. Seventh Edition. Elsevier, 2007

John Thomchick, J. P. McKelvey. Anharmonic vibration of an 'ideal' Hooke's law oscillator. Am. J. Phys. 46 (1) jan. 1978, pp. 40-45