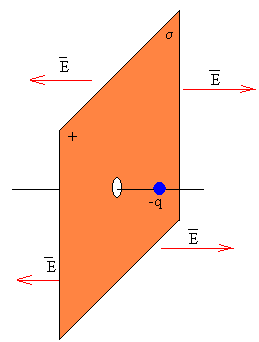
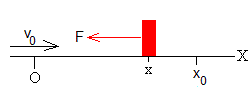
Consideremos una partícula de masa m cargada con una carga negativa q, en las proximidades de una placa indefinida cargada con una densidad de carga positiva σ C/m².

En la placa se ha hecho un pequeño agujero para que pueda pasar la partícula cargada, tal como se muestra en la figura

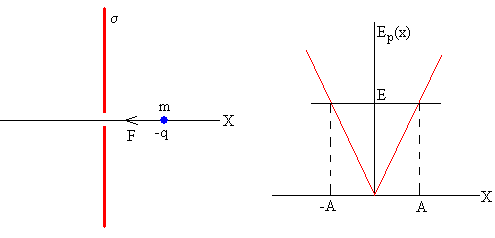
La fuerza que ejerce el campo eléctrico producido por una placa plana sobre la carga negativa q, es constante en módulo y de sentido contrario al campo eléctrico

${\displaystyle F=\frac{\sigma }{2{\epsilon }_0}q}$

• Cuando la partícula está a la derecha x>0 de la placa, la fuerza es negativa F<0

• Cuando la partícula está a la izquierda x<0 de la placa, la fuerza es positiva F>0

La energía potencial E_p(x) correspondiente a la fuerza conservativa F, es una función que tiene forma de V con el vértice en la posición de equilibrio x=0.

${\displaystyle E_p(x)=\frac{\sigma q}{2{\epsilon }_0}\left|x\right|}$

Esta función no se puede desarrollar en serie alrededor de x=0.

Un ejemplo más de este tipo de oscilador, es el movimiento de una pieza de dieléctrico entre las placas de un condensador conectado a una batería.

Oscilaciones libres

La posición y velocidad de la partícula en cualquier instante t se calculan mediante las ecuaciones del movimiento uniformemente acelerado

Denominamos f=F/m

• Primera etapa:



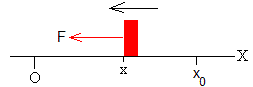
Desde la posición inicial x=x₀ a la posición x=0

${\displaystyle v=-f·tx=x_0-\frac{1}{2}f·t^2}$

Llega al origen en el instante t₀, y el módulo de su velocidad es v₀.

${\displaystyle t_0=\sqrt{\frac{2x_0}{f}}{v}_0=\sqrt{2f·x_0}}$

• Segunda etapa



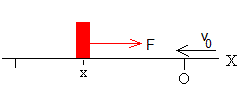
Desde que sale del origen hasta que regresa al mismo punto bajo la acción de la fuerza constante F.

${\displaystyle v=-v_0+f(t-t_0)x=-v_0(t-t_0)+\frac{1}{2}f{(t-t_0)}^2}$

Regresa al origen en el instante t=3·t₀, con velocidad v₀.

• Tercera etapa



Desde que sale del origen x=0, hasta que regresa a la posición inicial x=x₀

${\displaystyle v=v_0-f(t-3t_0)x=v_0(t-3t_0)-\frac{1}{2}f{(t-3t_0)}^2}$

Llega a la posición inicial x=x₀ en el instante 4·t₀, con velocidad nula v=0.

El periodo P es cuatro veces el tiempo t₀ que tarda en llegar por primer a vez al origen x=0, desde la posición inicial x=x₀, que es la amplitud A de la oscilación

${\displaystyle P=4\sqrt{\frac{2A}{f}}}$

El periodo P depende de la amplitud A

Expresamos de forma alternativa, las ecuaciones del movimiento, en términos del periodo P y la amplitud A, teniendo en cuenta que, v₀=8A/P y f=32A/P²

${\displaystyle \begin{array}{l}0\le t<\frac{P}{4}\{\begin{array}{l}v=-\frac{8A}{P}\left(4\frac{t}{P}\right)\\ x=A\left(1-16\frac{t^2}{P^2}\right)\end{array}\\ \frac{P}{4}\le t<\frac{3}{4}P\{\begin{array}{l}v=\frac{8A}{P}\left(-2+4\frac{t}{P}\right)\\ x=A\left(3-16\frac{t}{P}+16\frac{t^2}{P^2}\right)\end{array}\\ \frac{3}{4}P\le t<P\{\begin{array}{l}v=\frac{8A}{P}\left(4-4\frac{t}{P}\right)\\ x=A\left(-15+32\frac{t}{P}-16\frac{t^2}{P^2}\right)\end{array}\end{array}}$

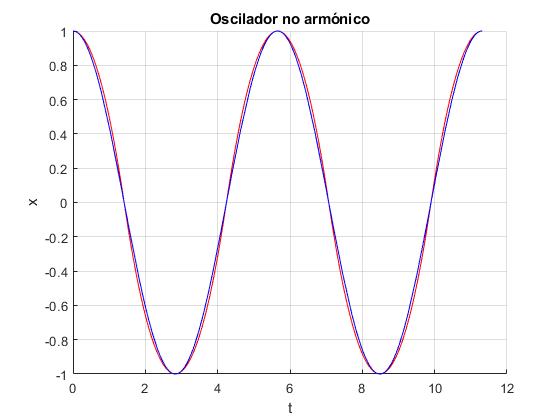
Representamos la posición x del móvil en función del tiempo t, (en color rojo) y la comparamos con el movimiento armónico simple de la misma amplitud A y periodo P, x=Acos(2πt/P)(en color azul)

A=1; %amplitud, posición inicial
f=1; %fuerza/masa
P=4*sqrt(2*A/f); %periodo
hold on
n=2; %oscilaciones
t=linspace(0,P,100);
x=(t>=0 &t<P/4).*(1-16*t.^2/P^2)+(t>=P/4 & t<3*P/4).*(3-16*t/P+16*t.^2/P^2)
+(t>=3*P/4 & t<=P).*(-15+32*t/P-16*t.^2/P^2);
for i=1:n
    plot(t+(i-1)*P,A*x, 'r') %no armónico
end
fplot(@(t) A*cos(2*pi*t/P),[0,n*P],'b') %armónico
hold off
grid on
xlabel('t')
ylabel('x')
title('Oscilador no armónico')

Observamos que la diferencia es pequeña

Análisis armónico

El desarrollo en serie de Fourier de la función periódica f(t) de periodo P es

${\displaystyle \begin{array}{l}f(t)=\frac{a_0}{2}+{\displaystyle \sum _{k=1}^{\infty }\left(a_k\cos \frac{2k\pi t}{P}+b_k\sin \frac{2k\pi t}{P}\right)}\\ \begin{array}{l}{a}_k=\frac{2}{P}\underset{0}{\overset{P}{{\displaystyle \int }}}f(t)\cos \frac{2k\pi t}{P}dt\hfill \\ b_k=\frac{2}{P}\underset{0}{\overset{P}{{\displaystyle \int }}}f(t)\sin \frac{2k\pi t}{P}dt\hfill \end{array}\end{array}}$

El cálculo de los coeficientes a_k y b_k es muy laborioso por lo que preparamos un script para determinar los primeros términos del desarrollo en serie de Fourier. Al ser una función par, comprobamos que los coeficientes b_k son nulos

syms t A P;
f1=A*(1-16*t^2/P^2);
f2=A*(3-16*t/P+16*t^2/P^2);
f3=A*(-15+32*t/P-16*t^2/P^2);
a=@(k) (int(f1*cos(2*k*pi*t/P),0,P/4)+int(f2*cos(2*k*pi*t/P),P/4,3*P/4)+
int(f3*cos(2*k*pi*t/P),3*P/4,P))*2/P;
b=@(k) (int(f1*sin(2*k*pi*t/P),0,P/4)+int(f2*sin(2*k*pi*t/P),P/4,3*P/4)+
int(f3*sin(2*k*pi*t/P),3*P/4,P))*2/P;
fs=(int(f1,0,P/4)+int(f2,P/4,3*P/4)+int(f3,3*P/4,P))/P;
for k=1:6
    fs=fs+a(k)*cos(2*k*pi*t/P)+b(k)*sin(2*k*pi*t/P);
end
f=subs(fs,{P,A},{4*sqrt(2),1})
ezplot(f,[0,6])
grid on
xlabel('t')
ylabel('x')
title('Oscilador no armónico')

Utilizamos el comando latext de MATLAB en combinación con MathType para mostar los primeros términos del desarrollo en serie que guarda la variable simbólica fs

>> latex(fs)
ans =
\frac{32\, A\, \cos\!\left(\frac{2\, \pi\, t}{P}\right)}{{\pi}^3} - 
\frac{32\, A\, \cos\!\left(\frac{6\, \pi\, t}{P}\right)}{27\, {\pi}^3} +
 \frac{32\, A\, \cos\!\left(\frac{10\, \pi\, t}{P}\right)}{125\, {\pi}^3}

${\displaystyle \frac{32A\cos \text{}\left(\frac{2\pi t}{P}\right)}{{\pi }^3}-\frac{32A\cos \text{}\left(\frac{6\pi t}{P}\right)}{27{\pi }^3}+\frac{32A\cos \text{}\left(\frac{10\pi t}{P}\right)}{125{\pi }^3}}$

O bien, de forma más compacta

${\displaystyle f(t)=32\frac{A}{{\pi }^3}\left(\frac{\cos \text{}\left(\frac{1·2\pi t}{P}\right)}{1}-\frac{\cos \text{}\left(\frac{3·2\pi t}{P}\right)}{3^3}+\frac{\cos \text{}\left(\frac{5·2\pi t}{P}\right)}{5^3}-\mathrm{....}\right)}$

Como 32/π³=1.0320.., y el segundo término es 1/27 veces el primero, el tercero 1/125 veces el primero, etc. La aproximación armónica x=Acos(2πt/P) difiere muy poco de la exacta, tal como hemos apreciado en la figura anterior

Procedimiento numérico

Definimos la función signo, sign(x)

${\displaystyle \text{sign}(x)\{\begin{array}{l}1x>0\\ 0x=0\\ -1x<0\end{array}}$

La fuerza F que se ejerce sobre la partícula es constante, pero cambia de sentido, si x>0, entonces F<0, en cambio si x<0, entonces F>0. La ecuación del movimiento se escribe

${\displaystyle \frac{d^{2}x}{d{t}^2}=-f\text{sign}(x)}$

Resolvemos la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales: en el instante t=0, x=x₀, v=0, parte del reposo

Creamos un script para representar la posición x de la partícula en función del tiempo t.

x0=1; %posición inicial, parte del reposo
f=1; %fuerza/masa
g=@(t,x) [x(2);-f*sign(x(1))]; 
[t,x]=ode45(g,[0,12],[x0,0]);
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('x');
title('Oscilador no armónico')

Actividades

Se introduce

• El valor del campo eléctrico producido por la placa plana positiva σ/(2є₀), en el control titulado Campo

• La posición inicial de la partícula, su distancia a la placa cargada, en el control titulado Posición

• La carga y la masa de la partícula se fijan el valor m=q=1

Se pulsa el botón titulado Nuevo

Se observa el movimiento de la partícula.

A la derecha se representa la energía potencial E_p(x). La recta horizontal es la energía total, y la recta vertical está dividida en dos porciones de color rojo y azul, la primera representa la energía potencial y la segunda, la energía cinética. También, se representa mediante una flecha la fuerza sobre la partícula.

Ejemplo

• Sea el valor del campo o de la fuerza sobre la partícula, F=60.
• La carga y la masa de la partícula valen, q=m=1
• La partícula parte de la posición inicial, A=0.7

El periodo de las oscilaciones es

${\displaystyle P=4\sqrt{\frac{2A}{f}}P=4\sqrt{\frac{2·0.7}{60}}=0.61}$

Oscilaciones amortiguadas

En este apartado, vamos a estudiar dos casos: fuerza de rozamiento constante y fuerza de rozamiento proporcional a la velocidad. Situaciones similares se estudian en las páginas tituladas Oscilador amortiguado por una fuerza de módulo constante (I) y Oscilaciones amortiguadas, respectivamente.

Fuerza de rozamiento constante

Supongamos que la partícula de masa m desliza en un plano horizontal con rozamiento cuyo coeficiente estático es μ_s y cinético μ_k≤μ_s. Supondremos que la fuerza F es mayor que μ_smg

Denominamos f=F/m>μ_sg

1. Movimiento hacia la izquierda, la partícula parte de la posición x₀ en el instante t=t₀=0 en reposo y se mueve hacia el origen



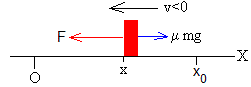
Cuando el bloque se mueve hacia la izquierda (v<0), la ecuación del movimiento es

ma=-F+ μ_kmg,

La posición y velocidad de la partícula son

${\displaystyle \begin{array}{l}x=x_0+\frac{1}{2}\left(-f+{\mu }_{k}g\right)t^2\\ v=\left(-f+{\mu }_{k}g\right)t\end{array}}$

El tiempo t₁ que tarda en llegar al origen x=0 y la velocidad v₁ de la partícula son

${\displaystyle \begin{array}{l}{t}_1=\sqrt{\frac{2x_0}{f-{\mu }_{k}g}}\\ v_1=-\sqrt{2(f-{\mu }_{k}g)x_0}\end{array}}$

2. Movimiento hacia la izquierda, la partícula parte del origen en el instante t=0 con velocidad inicial v₁ hasta que alcanza la posición x₂ en reposo



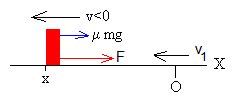
Cuando el bloque se mueve hacia la izquierda (v<0), la ecuación del movimiento es

ma=F+ μ_kmg,

La posición y velocidad de la partícula son

${\displaystyle \begin{array}{l}x=v_{1}t+\frac{1}{2}\left(f+{\mu }_{k}g\right)t^2\\ v=v_1+\left(f+{\mu }_{k}g\right)t\end{array}}$

El tiempo t₂ que tarda en detenerse y la posición x₂ son

${\displaystyle \begin{array}{l}{t}_2=\frac{-v_1}{f+{\mu }_{k}g}=\frac{\sqrt{2(f-{\mu }_{k}g)x_0}}{f+{\mu }_{k}g}\\ x_2=-\frac{(f-{\mu }_{k}g)}{f+{\mu }_{k}g}{x}_0\end{array}}$

3. Movimiento hacia la derecha, la partícula parte de la posición x₂ en reposo en el instante t=0 y se mueve hacia el origen



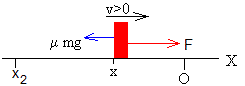
Cuando el bloque se mueve hacia la derecha(v>0), la ecuación del movimiento es

ma=F- μ_kmg,

La posición y velocidad de la partícula son

${\displaystyle \begin{array}{l}x=x_2+\frac{1}{2}\left(f-{\mu }_{k}g\right)t^2\\ v=\left(f-{\mu }_{k}g\right)t\end{array}}$

El tiempo t₃ que tarda en llegar al origen x=0 y la velocidad v₃ de la partícula son

${\displaystyle \begin{array}{l}{t}_3=\sqrt{\frac{-2x_2}{f-{\mu }_{k}g}}=\sqrt{\frac{2x_0}{f+{\mu }_{k}g}}\\ v_3=\sqrt{-2(f-{\mu }_{k}g)x_2}=(f-{\mu }_{k}g)\sqrt{\frac{2x_0}{f+{\mu }_{k}g}}\end{array}}$

4. Movimiento hacia la derecha, la partícula parte del origen en el instante t=0 con velocidad inicial v₃ hasta que alcanza la posición x₄ en reposo



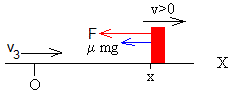
Cuando el bloque se mueve hacia la derecha (v>0), la ecuación del movimiento es

ma=-F-μ_kmg,

La posición y velocidad de la partícula son

${\displaystyle \begin{array}{l}x=v_{3}t+\frac{1}{2}\left(-f-{\mu }_{k}g\right)t^2\\ v=v_3+\left(-f-{\mu }_{k}g\right)t\end{array}}$

El tiempo t₄ que tarda en detenerse y la posición x₄ son

${\displaystyle \begin{array}{l}{t}_4=\frac{v_3}{f+{\mu }_{k}g}=\frac{f-{\mu }_{k}g}{f+{\mu }_{k}g}\sqrt{\frac{2x_0}{f+{\mu }_{k}g}}\\ x_4=\frac{{\left(f-{\mu }_{k}g\right)}^2}{{\left(f+{\mu }_{k}g\right)}^2}{x}_0\end{array}}$

La posición inicial para el siguiente periodo t₀=t₁+t₂+t₃+t₄ es x₀=x₄

Representamos la posición x de la partícula en función del tiempo t, durante cuatro oscilaciones, para f=1 y μ_kg=0.1. La partícula parte de la posición inicial x₀=1, en reposo

x0=1; %posición inicial
f=1; %fuerza/masa
mu=0.1; %rozamiento, mu*g
n=4; %oscilaciones
hold on

t0=0;
for i=1:n
    t1=t0+sqrt(2*x0/(f-mu));
    t2=t1+sqrt(2*(f-mu)*x0)/(f+mu);
    t3=t2+sqrt(2*x0/(f+mu));
    t4=t3+(f-mu)*sqrt(2*x0/(f+mu))/(f+mu);
    v1=-sqrt(2*(f-mu)*x0);
    v3=(f-mu)*sqrt(2*x0/(f+mu));
    x2=-(f-mu)*x0/(f+mu);
    x4=x0*(f-mu)^2/(f+mu)^2;
    t=linspace(t0,t4,100);
    x=(t>=t0 & t<t1).*(x0-(f-mu)*(t-t0).^2/2)+(t>=t1 & t<t2).*(v1*(t-t1)+
(f+mu)*(t-t1).^2/2)+(t>=t2 & t<t3).*(x2+(f-mu)*(t-t2).^2/2)+
(t>=t3 & t<=t4).*(v3*(t-t3)-(f+mu)*(t-t3).^2/2);
   plot(t,x,'r')
    x0=x4;
   t0=t4;
end

hold off
grid on
xlabel('t')
ylabel('x')
title('Oscilador no armónico, amortiguado')

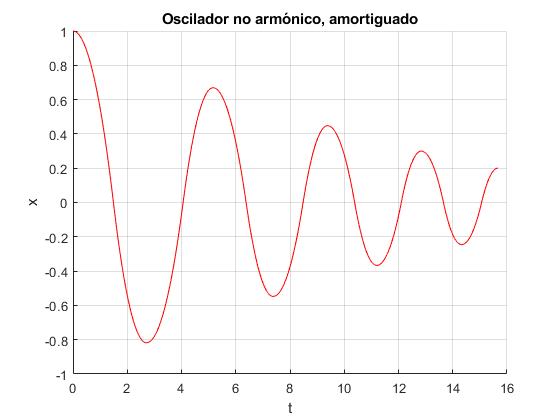
Representamos la velocidad v de la partícula en función del tiempo t, durante cuatro oscilaciones, para f=1 y μ_kg=0.1. La partícula parte de la posición inicial x₀=1, en reposo

x0=1; %posición inicial
f=1; %fuerza/masa
mu=0.1; %rozamiento, mu*g
n=4; %oscilaciones
hold on

t0=0;
for i=1:n
    t1=t0+sqrt(2*x0/(f-mu));
    t2=t1+sqrt(2*(f-mu)*x0)/(f+mu);
    t3=t2+sqrt(2*x0/(f+mu));
    t4=t3+(f-mu)*sqrt(2*x0/(f+mu))/(f+mu);
    v1=-sqrt(2*(f-mu)*x0);
    v3=(f-mu)*sqrt(2*x0/(f+mu));
    x2=-(f-mu)*x0/(f+mu);
    x4=x0*(f-mu)^2/(f+mu)^2;
    t=linspace(t0,t4,100);
    v=(t>=t0 & t<t1).*(-(f-mu)*(t-t0))+(t>=t1 & t<t2).*(v1+(f+mu)*(t-t1))+
(t>=t2 & t<t3).*((f-mu)*(t-t2))+(t>=t3 & t<=t4).*(v3-(f+mu)*(t-t3));
     plot(t,v,'b')
   x0=x4;
   t0=t4;
end
hold off
grid on
xlabel('t')
ylabel('v')
title('Oscilador no armónico, amortiguado')

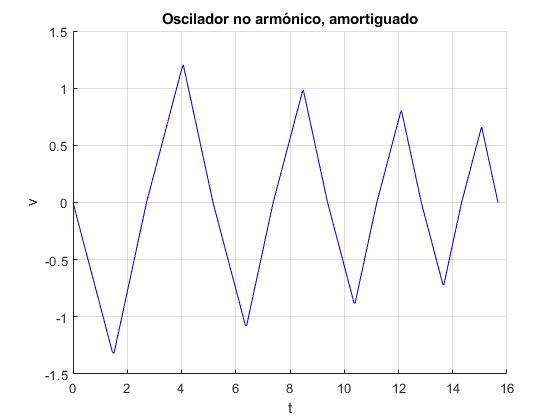
Comprobamos que el periodo, o tiempo que tarda en describir una oscilación no es constante, va disminuyendo con el número de oscilaciones

x0=1; %posición inicial
f=1; %fuerza/masa
mu=0.1; %rozamiento, mu*g
n=20; %oscilaciones
P=zeros(1,n);
t0=0;
for i=1:n
    t1=t0+sqrt(2*x0/(f-mu));
    t2=t1+sqrt(2*(f-mu)*x0)/(f+mu);
    t3=t2+sqrt(2*x0/(f+mu));
    t4=t3+(f-mu)*sqrt(2*x0/(f+mu))/(f+mu);
    v1=-sqrt(2*(f-mu)*x0);
    v3=(f-mu)*sqrt(2*x0/(f+mu));
    x2=-(f-mu)*x0/(f+mu);
    x4=x0*(f-mu)^2/(f+mu)^2;
   x0=x4;
   P(i)=t4-t0;
   t0=t4;
end

plot(1:n,P, 'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
grid on
xlabel('n')
ylabel('P')
title('Oscilador no armónico, amortiguado')

Procedimiento numérico

La fuerza F que se ejerce sobre la partícula es constante, pero cambia de sentido, si x>0, entonces F<0, en cambio si x<0, entonces F>0. La fuerza de rozamiento es siempre de sentido contrario a la velocidad. La ecuación del movimiento se escribe

${\displaystyle \[ \frac{d^{2}x}{d{t}^2}=-f·\text{sign}(x)-{\mu }_{k}g·\text{sign}\left(\frac{dx}{dt}\right) \]}$

Resolvemos la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales: en el instante t=0, x=x₀, v=0, parte del reposo

Creamos un script para representar la posición x de la partícula en función del tiempo t.

x0=1; %amplitud
f=1; %fuerza/masa
mu=0.1; %rozamiento, mu*g

f1=@(t,x) [x(2);-f*sign(x(1))-mu*sign(x(2))]; 
[t,x]=ode45(f1,[0,t4],[x0,0]);
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('x')
title('Oscilador no armónico, amortiguado')

Fuerza de rozamiento proporcional a la velocidad

Sobre la partícula además de la fuerza F, supondremos que actúa una fuerza de rozamiento porporcional a la velocidad v=dx/dt y de sentido contrario a esta

• Primera etapa:



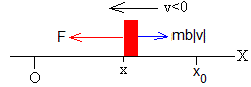
Desde la posición inicial x=x₀ a la posición x=0, la partícula se mueve hacia el origen, v<0, bajo la acción de una fuerza F, negativa y una fuerza de rozamiento positiva. La ecuación del movimiento es

${\displaystyle \frac{dv}{dt}=-f-bv,v<0}$

sabiendo que en el instante t=0, la partícula parte del reposo v=0

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{v}{\int }}\frac{dv}{f+bv}}=-{\displaystyle \underset{0}{\overset{t}{\int }}dt}\hfill \\ v=-\frac{f}{b}\left(1-\exp (-bt)\right)\hfill \end{array}}$

Integramos de nuevo v=dx/dt para obtener la posición x en función del tiempo t, sabiendo que en el instante t=0, x=x₀

${\displaystyle \begin{array}{l}{\displaystyle \underset{x_0}{\overset{x}{\int }}dx}=-\frac{f}{b}{\displaystyle \underset{0}{\overset{t}{\int }}\left(1-\exp (-bt)\right)}dt\hfill \\ x=x_0-\frac{f}{b}\left(t+\frac{1}{b}\exp (-bt)-\frac{1}{b}\right)\hfill \end{array}}$

Llega al origen x=0 en el instante t₁, raíz de la ecuación trascendente

${\displaystyle x_0-\frac{f}{b}\left(t+\frac{1}{b}\exp (-bt)-\frac{1}{b}\right)=0}$

con velocidad

${\displaystyle v_1=-\frac{f}{b}\left(1-\exp (-b{t}_1)\right)}$

• Segunda etapa



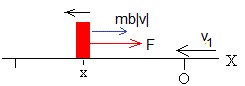
Desde que sale del origen hasta que regresa al mismo punto bajo la acción de la fuerza constante F (positiva) y una fuerza de rozamiento de sentido contrario a la velocidad.

${\displaystyle \frac{dv}{dt}=f-bv}$

sabiendo que en el instante t=t₁, la partícula parte con velocidad v₁

${\displaystyle \begin{array}{l}{\displaystyle \underset{v_1}{\overset{v}{\int }}\frac{dv}{f-bv}}={\displaystyle \underset{t_1}{\overset{t}{\int }}dt}\hfill \\ v=\left(v_1-\frac{f}{b}\right)\exp \left(-b(t-t_1)\right)+\frac{f}{b}\hfill \end{array}}$

Integramos de nuevo v=dx/dt para obtener la posición x en función del tiempo t, sabiendo que en el instante t=t₁, parte del origen, x=0

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{x}{\int }}dx}={\displaystyle \underset{t_1}{\overset{t}{\int }}\left\{\left(v_1-\frac{f}{b}\right)\exp \left(-b(t-t_1)\right)+\frac{f}{b}\right\}}dt\hfill \\ x=\frac{1}{b}\left\{\left(v_1-\frac{f}{b}\right)\left(1-\exp \left(-b(t-t_1)\right)\right)+f(t-t_1)\right\}\hfill \end{array}}$

Llega al origen en el instante t₂, raíz de la ecuación trascendente, x=0 con velocidad

${\displaystyle v_2=\left(v_1-\frac{f}{b}\right)\exp \left(-b(t_2-t_1)\right)+\frac{f}{b}}$

• Tercera etapa



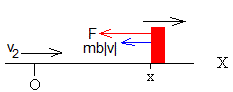
Desde que sale del origen x=0, con velocidad v₂ hasta que su velocidad se hace nula v=0

${\displaystyle \frac{dv}{dt}=-f-bv}$

Integramos la ecuación diferencial, sabiendo que en el instante t=t₂, la partícula parte con velocidad v₂

${\displaystyle \begin{array}{l}{\displaystyle \underset{v_2}{\overset{v}{\int }}\frac{dv}{f+bv}}=-{\displaystyle \underset{t_2}{\overset{t}{\int }}dt}\hfill \\ v=\left(v_2+\frac{f}{b}\right)\exp \left(-b(t-t_2)\right)-\frac{f}{b}\hfill \end{array}}$

Integramos de nuevo v=dx/dt para obtener la posición x en función del tiempo t, sabiendo que en el instante t=t₂, parte del origen, x=0

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{x}{\int }}dx}={\displaystyle \underset{t_1}{\overset{t}{\int }}\left\{\left(v_2+\frac{f}{b}\right)\exp \left(-b(t-t_2)\right)-\frac{f}{b}\right\}}dt\hfill \\ x=\frac{1}{b}\left\{\left(v_2+\frac{f}{b}\right)\left(1-\exp \left(-b(t-t_2)\right)\right)-f(t-t_2)\right\}\hfill \end{array}}$

Se detiene v=0 en el instante t₃, raíz de la ecuación trascendente,

${\displaystyle \left(v_2+\frac{f}{b}\right)\exp \left(-b(t-t_2)\right)-\frac{f}{b}=0}$

En la posición

${\displaystyle x_1=\frac{1}{b}\left\{-\left(v_2+\frac{f}{b}\right)\exp \left(-b(t_3-t_2)\right)+\left(v_2+\frac{f}{b}\right)-f(t_3-t_2)\right\}}$

t₃ es el primer periodo de la oscilación amortiguada

y así, sucesivamente

x0=1; %posción inicial
f=1; %fuerza
b=1/20; %amortiguamiento
n=5; %oscilaciones
t0=0; 
hold on
for i=1:n % oscilaciones    
    P=4*sqrt(2*x0/f); %periodo no amortiguado
    v=@(t) -(1-exp(-b*t))*f/b;
    x=@(t) x0-(t-(1-exp(-b*t))/b)*f/b;
    t1=fzero(x, P/4);
    tt=linspace(0,t1,50);
    plot(tt+t0,x(tt),'r')

    v0=v(t1); %velocidad inicial
    v=@(t) (v0-f/b)*exp(-b*(t-t1))+f/b;
    x=@(t) ((v0-f/b)*(1-exp(-b*(t-t1)))+f*(t-t1))/b;
    t2=fzero(x,3*P/4);
    tt=linspace(t1,t2,100);
    plot(tt+t0,x(tt),'r')

    v0=v(t2);
    v=@(t) (v0+f/b)*exp(-b*(t-t2))-f/b;
    x=@(t) ((v0+f/b)*(1-exp(-b*(t-t2)))-f*(t-t2))/b;
    t3=fzero(v,P);
    x0=x(t3);
    tt=linspace(t2,t3,50);
    plot(tt+t0,x(tt),'r')
    t0=t0+t3;
end

hold off
grid on
xlabel('t')
ylabel('x')
title('Oscilador amortiguado no armónico')

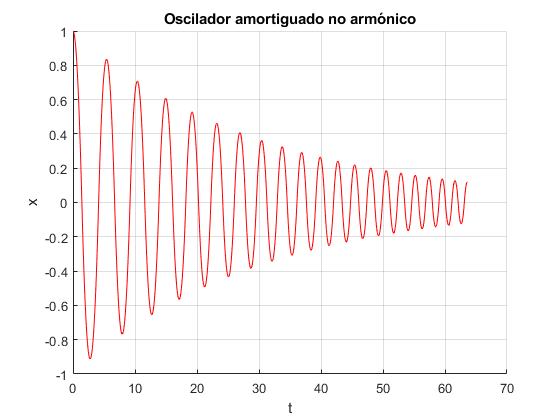
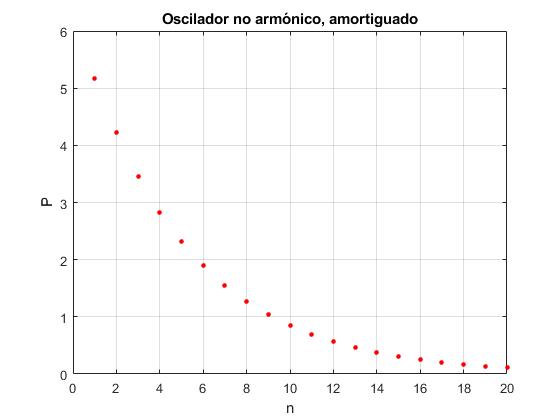
Comprobamos que el periodo, o tiempo que tarda en describir una oscilación no es constante, va disminuyendo con el número de oscilaciones

x0=1; %posción inicial
f=1; %fuerza
b=1/20; %amortiguamiento
t0=0; 
n=20; %oscilaciones
Pe=zeros(1,n);
for i=1:n 
    P=4*sqrt(2*x0/f); %periodo no amortiguado
    v=@(t) -(1-exp(-b*t))*f/b;
    x=@(t) x0-(t-(1-exp(-b*t))/b)*f/b;
    t1=fzero(x, P/4);

    v0=v(t1);
    v=@(t) (v0-f/b)*exp(-b*(t-t1))+f/b;
    x=@(t) ((v0-f/b)*(1-exp(-b*(t-t1)))+f*(t-t1))/b;
    t2=fzero(x,3*P/4);

    v0=v(t2);
    v=@(t) (v0+f/b)*exp(-b*(t-t2))-f/b;
    x=@(t) ((v0+f/b)*(1-exp(-b*(t-t2)))-f*(t-t2))/b;
    t3=fzero(v,P);
    x0=x(t3);
    t0=t0+t3;
    Pe(i)=t3;   
end
plot(1:n,Pe, 'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')

grid on
xlabel('n')
ylabel('P')
title('Oscilador amortiguado no armónico')

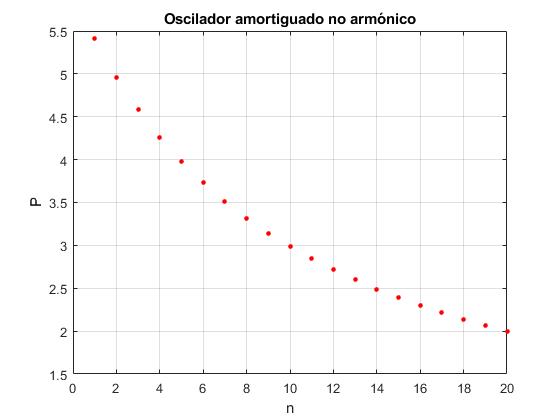
Procedimiento numérico

La fuerza F que se ejerce sobre la partícula es constante, pero cambia de sentido, si x>0, entonces F<0, en cambio si x<0, entonces F>0. La fuerza de rozamiento es siempre de sentido contrario a la velocidad. La ecuación del movimiento se escribe

${\displaystyle \frac{d^{2}x}{d{t}^2}=-f\text{sign}(x)-b\frac{dx}{dt}}$

Resolvemos la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales: en el instante t=0, x=x₀, v=0, parte del reposo

x0=1; %posición inicial, parte del reposo
f=1; %fuerza/masa
P=4*sqrt(2*x0/f); %periodo no amortiguado
b=1/20; %amortiguamiento
f=@(t,x) [x(2);-b*x(2)-f*sign(x(1))]; 
[t,x]=ode45(f,[0,4*P],[x0,0]);
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('x');
title('oscilador no armónico amortiguado')

Referencias

Ian R. Gatland, Theory of nonharmonic oscillator, Am. J. Phys. 59 (2) February 1991, pp. 155-158