Demostración de la ley de Faraday

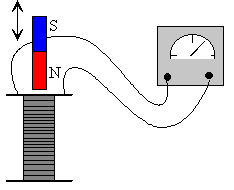
La ley de Faraday no es fácil de entender para los estudiantes. Para introducir esta ley fundamental en la Física se realizan las siguientes experiencias con una bobina, un amperímetro y un imán:

Se sitúa el imán en reposo dentro del solenoide.
Se introduce despacio/deprisa el imán en el solenoide.
Se saca despacio/deprisa el imán del solenoide.
Se observa el movimiento de la aguja del amperímetro
Se aplica la ley de Lenz, para determinar el sentido de la corriente inducida.

Flujo y f.e.m.

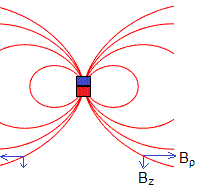
En la página, Campo magnético producido por una imán hemos supuesto que un imán se comporta como un dipolo magnético de momento μ. Las componentes del campo son

$\begin{array}{l} B_{ρ} = \frac{μ_{0} μ}{4 π} \frac{3 ρ z}{{(\sqrt{z^{2} + ρ^{2}})}^{5}} \\ B_{z} = \frac{μ_{0} μ}{4 π} \frac{2 z^{2} - ρ^{2}}{{(\sqrt{z^{2} + ρ^{2}})}^{5}} \end{array}$

El flujo del campo producido por el imán a través de una bobina de radio a formada por de N espiras apretadas es.

$Φ = N \int_{S} \vec{B} \cdot \vec{d S} = N \int_{S} (B_{ρ} \hat{j} + B_{z} \hat{k}) \cdot d S \cdot \hat{k} = - N \int_{S} B_{z} \cdot d S$

El flujo depende solamente de la componente B_z del campo magnético

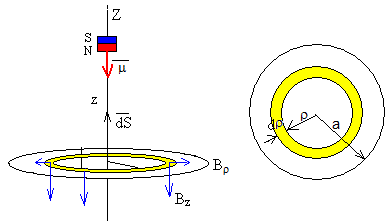
El elemento diferencial de superficie dS, es el área de un anillo de radio ρ y de espesor dρ, su valor es dS=2πρ·dρ

$\begin{array}{l} Φ = - N \int_{0}^{a} \frac{μ_{0} \cdot μ}{4 π} (\frac{3 z^{2}}{{(\sqrt{ρ^{2} + z^{2}})}^{5}} - \frac{1}{{(\sqrt{ρ^{2} + z^{2}})}^{3}}) 2 π ρ \cdot d ρ \\ Φ = - \frac{μ_{0} N \cdot μ}{4} (3 z^{2} \int_{0}^{a} \frac{2 ρ \cdot d ρ}{{(\sqrt{ρ^{2} + z^{2}})}^{5}} - \int_{0}^{a} \frac{2 ρ \cdot d ρ}{{(\sqrt{ρ^{2} + z^{2}})}^{3}}) = - \frac{μ_{0} μ N \cdot a^{2}}{2 {(\sqrt{b^{2} + z^{2}})}^{3}} \end{array}$

Aplicando la ley de Faraday

$V_{ε} = - \frac{d Φ}{d t} = - \frac{d Φ}{d z} \frac{d z}{d t} = - \frac{d Φ}{d z} (- v) = \frac{3 μ_{0} μ N a^{2}}{2} \frac{z v}{{(a^{2} + z^{2})}^{5 / 2}}$

El imán se mueve con velocidad constante

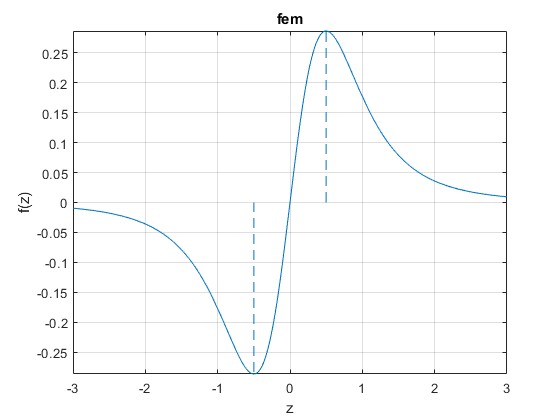
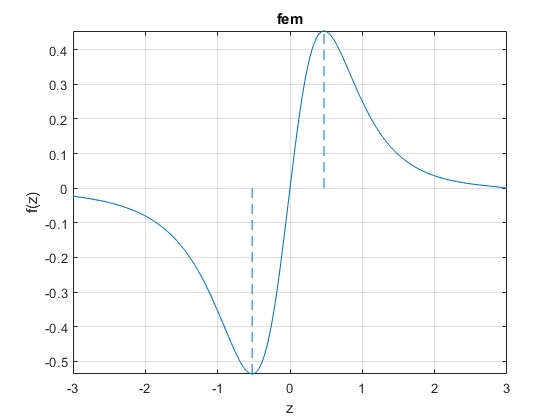
Esta función tiene dos extremos (un máximo y un mínimo) que calculamos haciendo dV_ε/dz=0 y se sitúan en z=±a/2. La fem es proporcional a

$\begin{array}{l} y = \frac{z}{{(z^{2} + a^{2})}^{5 / 2}} \\ \frac{d y}{d z} = \frac{{(z^{2} + a^{2})}^{5 / 2} - \frac{5}{2} 2 z {(z^{2} + a^{2})}^{3 / 2} z}{{(z^{2} + a^{2})}^{5}} = 0 \\ z^{2} + a^{2} - 5 z^{2} = 0 \\ 4 z^{2} = a^{2}, {\begin{cases} z = \frac{a}{2} \\ z = - \frac{a}{2} \end{cases} \end{array}$

presenta un mínimo para -a/2 y un máximo para a/2, tal como se aprecia en la gráfica y se calcula con MATLAB

a=1;
f=@(z) z./(z.^2+a^2).^(5/2);
fplot(f,[-3,3])
line([a/2,a/2],[0,f(a/2)], 'lineStyle','--')
line([-a/2,-a/2],[0,f(-a/2)], 'lineStyle','--')
grid on
xlabel('z')
ylabel('f(z)')
title('fem')

El valor máximo de la fem es

$V_{m} = \frac{24 μ_{0} μ N v}{{(\sqrt{5})}^{5} a^{2}}$

El valor máximo de la fem V_ε es más grande para bobinas de menor radio a.

a=0.03; %radio de la bobina
N=400;  %número de espiras 
v=0.80; %velocidad del imán
m=2.35; %momento magnético del imán
flujo=@(z) -10*4*pi*1e-7*m*N*a^2/(2*(a^2+z^2)^(3/2));  %flujo
fem= @(z) 3*4*pi*1e-7*m*N*a^2*z*v/(2*(a^2+z^2)^(5/2)); %fem
hold on
fplot(flujo, [-0.1,0.1]);
fplot(fem, [-0.1,0.1]);
hold off
xlabel('z(m)');
ylabel('V_\epsilon, \Phi')
grid on
legend('Flujo','fem')
title('Demostración de la ley de Faraday')

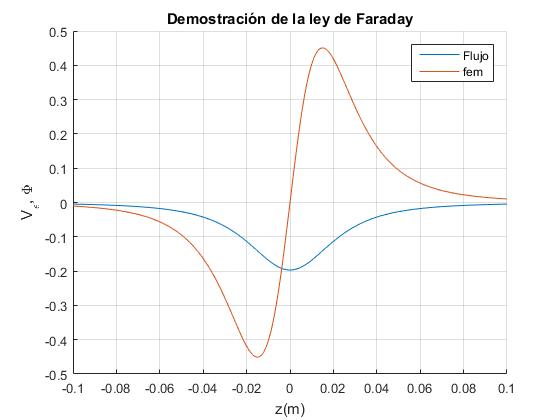
En la figura, se muestra el flujo (en color azul) y la fem (en color rojo).

Actividades

En la experiencia descrita en el artículo mencionado en las referencias, se usa un imán de 1.0 cm de espesor y de 0.9 cm de radio. Se determina experimentalmente su momento magnético μ, midiendo el campo magnético en distintas posiciones a lo largo de su eje Z. Poniendo r=z en la expresión de la componente B_z del campo magnético producido por el imán.

$B = \frac{μ_{0} μ}{2 π z^{3}}$

El valor experimental del momento dipolar magnético es de μ=2.35 Am².

El campo magnético producido por el imán atraviesa una bobina de N=400 espiras con una velocidad constante del orden de 70-90 cm/s. Los radios de las bobinas empleadas son del orden de 3 cm.

Ejemplo:

Supongamos que la bobina tiene a=3 cm de radio y la velocidad del imán es de v=80 cm/s. El valor máximo de la fem es de

$V_{m} = \frac{24 \cdot 4 \cdot π \cdot 10^{- 7} \cdot 2.35 \cdot 400 \cdot 0.8}{{(\sqrt{5})}^{5} \cdot {0.03}^{2}} = 0.45 V$

Se introduce los valores de los parámetros:

La velocidad constante del imán v en cm/s, en el control titulado Velocidad.
El radio a de la bobina en cm en el control titulado Radio.
El momento dipolar magnético se ha fijado en μ=2.35 Am².
El número de espiras de la bobina se ha fijado en N=400

Se pulsa en el botón titulado Nuevo.

Se observa el imán acercándose a la bobina, el campo magnético se incrementa rápidamente cuando el imán se encuentra cerca de la bobina. Se representa mediante un vector el flujo del campo magnético producido por el imán a través de las espiras de la bobina.

El movimiento de los puntos de color rojo situados sobre la bobina nos señala el sentido de la corriente inducida. El sentido antihorario se toma como positivo y el sentido horario como negativo.

Finalmente, se representa la fem (en color rojo) y el flujo (en color azul) en función de z, la distancia entre el imán y la bobina. Observamos que el máximo se sitúa en la posición z=-a/2, y el mínimo en la posición simétrica z=a/2. La separación entre le máximo y el mínimo es igual al radio de la bobina.

Radio (cm):
Velocidad (cm/s):

El imán cae libremente desde una altura z₀

Las ecuaciones del movimiento del imán son

${\begin{cases} v = g t \\ z = z_{0} - \frac{1}{2} g t^{2} \end{cases}$

La fem en función del tiempo es

$V_{ε} (t) = \frac{3 μ_{0} μ N a^{2}}{2} \frac{z_{0} - \frac{1}{2} g t^{2}}{{({(z_{0} - \frac{1}{2} g t^{2})}^{2} + a^{2})}^{5 / 2}} g t$

La fem en función de la altura z del imán

$V_{ε} (z) = \frac{3 μ_{0} μ N a^{2}}{2} \frac{z}{{(z^{2} + a^{2})}^{5 / 2}} \sqrt{2 g (z_{0} - z)}$

Los extremos se producen cuando

$\begin{array}{l} \frac{d V_{ε} (z)}{d z} = 0 \\ \frac{d}{d z} (\frac{z \sqrt{z_{0} - z}}{{(z^{2} + a^{2})}^{5 / 2}}) = 0 \\ (\sqrt{z_{0} - z} - \frac{z}{2 \sqrt{z_{0} - z}}) {(z^{2} + a^{2})}^{5 / 2} - \frac{5}{2} (2 z) {(z^{2} + a^{2})}^{3 / 2} z \sqrt{z_{0} - z} = 0 \\ \frac{2 z_{0} - 3 z}{2 \sqrt{z_{0} - z}} (z^{2} + a^{2}) - 5 z^{2} \sqrt{z_{0} - z} = 0 \\ (2 z_{0} - 3 z) (z^{2} + a^{2}) - 10 z^{2} (z_{0} - z) = 0 \\ 7 z^{3} - 8 z_{0} z^{2} - 3 a^{2} z + 2 z_{0} a^{2} = 0 \end{array}$

Los extremos (máximo y mínimo) son dos raíces reales de una ecuación de tercer grado

function fem
    a=1;
    z0=3;
    f=@(z) (z.*sqrt(z0-z))./(z.^2+a^2).^(5/2);
    fplot(f,[-3,3])
    raiz=raices_3([1,-8*z0/7,-3*a^2/7,2*z0*a^2/7]);
    disp(raiz)
    line([raiz(1),raiz(1)],[0,f(raiz(1))], 'lineStyle','--')
    line([raiz(3),raiz(3)],[0,f(raiz(3))], 'lineStyle','--')
     grid on
    xlabel('z')
    ylabel('f(z)')
    title('fem')

    function x = raices_3(p)
        Q=(p(2)*p(2)-3*p(3))/9;
        R=(2*p(2)^3-9*p(2)*p(3)+27*p(4))/54;
        x=zeros(3,1); %reserva memoria para un vector de tres elementos
        if (R*R)<(Q^3)
            tetha=acos(R/sqrt(Q^3));
            x(1)=-2*sqrt(Q)*cos(tetha/3)-p(2)/3;
            x(2)=-2*sqrt(Q)*cos((tetha+2*pi)/3)-p(2)/3;
            x(3)=-2*sqrt(Q)*cos((tetha-2*pi)/3)-p(2)/3;
        else
            A=-sign(R)*nthroot(abs(R)+sqrt(R*R-Q^3),3);
            if A==0
                B=0;
            else
                B=Q/A;
            end
            x(1)=(A+B)-p(2)/3;
            x(2)=-(A+B)/2-p(2)/3+(sqrt(3)*(A-B)/2)*sqrt(-1); %mejor que i
            x(3)=-(A+B)/2-p(2)/3-(sqrt(3)*(A-B)/2)*sqrt(-1);
        end
    end
end

Las tres raíces reales de la ecuación de tercer grado son

  -0.5231
    3.4810
    0.4707

Son válidas la primera y la tercera

Cuando la altura inicial del imán es grande comparado con el radio a, por ejemplo, z₀=10, los extremos se aproximan a ±a/2

Referencias

Kingman R., Clark Rowland S., Popescu S. An experimental observation of Faraday’s law of induction. Am. J. Phys. 70 (6) June 2002, pp. 595-598.