Coordenadas rectangulares

Las ecuaciones de Navier-Stokes para un fluido incompresible en coordenadas rectangulares son

• En forma vectorial

${\displaystyle \begin{array}{l}\nabla ·\overrightarrow{u}=0\\ {\rho }_f\left(\frac{\partial \overrightarrow{u}}{\partial t}+\overrightarrow{u}·\nabla \overrightarrow{u}\right)=-\nabla p+{\rho }_f\overrightarrow{g}+\eta \Delta \overrightarrow{u}\end{array}}$

La primera, es la ecuación de continuidad. p es la presión hidrostática y $\overrightarrow{g}$ la aceleración de la gravedad

• En coordenadas rectangulares

${\displaystyle \begin{array}{l}\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}+\frac{\partial u_z}{\partial z}=0\\ \{\begin{array}{l}{\rho }_f\left(\frac{\partial u_x}{\partial t}+u_x\frac{\partial u_x}{\partial x}+u_y\frac{\partial u_x}{\partial y}+u_z\frac{\partial u_x}{\partial z}\right)=-\frac{\partial p}{\partial x}+{\rho }_f{g}_x+\eta \left(\frac{{\partial }^2{u}_x}{\partial x^2}+\frac{{\partial }^2{u}_x}{\partial y^2}+\frac{{\partial }^2{u}_x}{\partial z^2}\right)\\ {\rho }_f\left(\frac{\partial u_y}{\partial t}+u_x\frac{\partial u_y}{\partial x}+u_y\frac{\partial u_y}{\partial y}+u_z\frac{\partial u_y}{\partial z}\right)=-\frac{\partial p}{\partial y}+{\rho }_f{g}_y+\eta \left(\frac{{\partial }^2{u}_y}{\partial x^2}+\frac{{\partial }^2{u}_y}{\partial y^2}+\frac{{\partial }^2{u}_y}{\partial z^2}\right)\\ {\rho }_f\left(\frac{\partial u_z}{\partial t}+u_x\frac{\partial u_z}{\partial x}+u_y\frac{\partial u_z}{\partial y}+u_z\frac{\partial u_z}{\partial z}\right)=-\frac{\partial p}{\partial z}+{\rho }_f{g}_z+\eta \left(\frac{{\partial }^2{u}_z}{\partial x^2}+\frac{{\partial }^2{u}_z}{\partial y^2}+\frac{{\partial }^2{u}_z}{\partial z^2}\right)\end{array}\end{array}}$

El tensor de esfuerzo viscoso (simétrico)

${\displaystyle \tau =\left(\begin{array}{ccc}{\tau }_{xx}& {\tau }_{xy}& {\tau }_{xz}\\ {\tau }_{yx}& {\tau }_{yy}& {\tau }_{yz}\\ {\tau }_{zx}& {\tau }_{zy}& {\tau }_{zz}\end{array}\right)=\left(\begin{array}{ccc}2\eta \frac{\partial u_x}{\partial x}& \eta \left(\frac{\partial u_x}{\partial y}+\frac{\partial u_y}{\partial x}\right)& \eta \left(\frac{\partial u_x}{\partial z}+\frac{\partial u_z}{\partial x}\right)\\ \eta \left(\frac{\partial u_y}{\partial x}+\frac{\partial u_x}{\partial y}\right)& 2\eta \frac{\partial u_y}{\partial y}& \eta \left(\frac{\partial u_y}{\partial z}+\frac{\partial u_z}{\partial y}\right)\\ \eta \left(\frac{\partial u_z}{\partial x}+\frac{\partial u_x}{\partial z}\right)& \eta \left(\frac{\partial u_z}{\partial y}+\frac{\partial u_y}{\partial z}\right)& 2\eta \frac{\partial u_z}{\partial z}\end{array}\right)}$

Representamos las fuerzas (por unidad de área) sobre un elemento de fluido

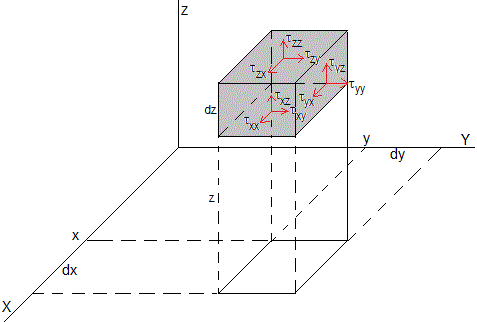
Estudiaremos un fluido incompresible entre dos placas planas paralelas que distan h. El problema a estudiar se reduce a dos dimensiones, se elimina la componente Z del sistema de ecuaciones diferenciales en derivadas parciales

${\displaystyle \begin{array}{l}\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}=0\\ \{\begin{array}{l}{\rho }_f\left(\frac{\partial u_x}{\partial t}+u_x\frac{\partial u_x}{\partial x}+u_y\frac{\partial u_x}{\partial y}\right)=-\frac{\partial p}{\partial x}+{\rho }_f{g}_x+\eta \left(\frac{{\partial }^2{u}_x}{\partial x^2}+\frac{{\partial }^2{u}_x}{\partial y^2}\right)\\ {\rho }_f\left(\frac{\partial u_y}{\partial t}+u_x\frac{\partial u_y}{\partial x}+u_y\frac{\partial u_y}{\partial y}\right)=-\frac{\partial p}{\partial y}+{\rho }_f{g}_y+\eta \left(\frac{{\partial }^2{u}_y}{\partial x^2}+\frac{{\partial }^2{u}_y}{\partial y^2}\right)\end{array}\end{array}}$

La placa superior se mueve con velocidad constante v

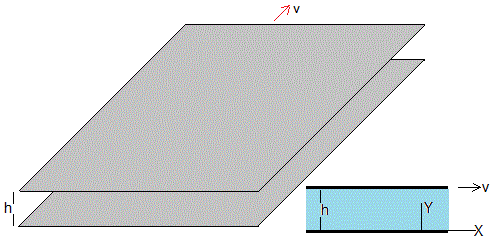
Supondremos

• En el estado es estacionario (no depende del tiempo), las derivadas respecto de t son nulas
• El flujo es laminar entre las dos placas planas paralelas y no cambia en la dirección X. La componente u_y y sus derivadas son nulas
• La presión p no depende de x, solamente de y

Condiciones de contorno

• En la placa inferior y=0, las componentes de la velocidad u_x=u_y=0
• En la placa superior y=h, las componentes de la velocidad u_x=v, u_y=0

El fluido en contacto con la placa se mueve con la misma velocidad

El sistema de tres ecuaciones diferenciales en derivadas parciales, se transforma en otro más simple

${\displaystyle \begin{array}{l}\frac{\partial u_x}{\partial x}=0\\ \{\begin{array}{l}\frac{{\partial }^2{u}_x}{\partial y^2}=0\\ -\frac{\partial p}{\partial y}-\rho g=0\end{array}\end{array}}$

La ecuación de continuidad nos indica que la componente u_x de la velocidad del fluido es función únicamente de y lo que simplifica las otras dos ecuaciones diferenciales en derivadas parciales

Integrando u_x dos veces

${\displaystyle \begin{array}{l}\frac{\partial u_x}{\partial y}=c_1\\ u_x=c_{1}y+c_2\end{array}}$

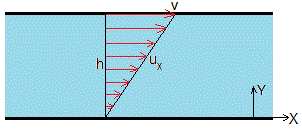
Las constantes c₁ y c₂ se determinan a partir de las condiciones de contorno: u_x(0)=0, c₂=0. u_x(h)=v, c₁=v/h

${\displaystyle u_x=\frac{v}{h}y}$

Integrando la presión p

${\displaystyle p=-\rho gy+p_0}$

Para y=0, la presión es p₀

La presión no afecta al movimiento del fluido

Esfuerzo viscoso

${\displaystyle \tau =\left(\begin{array}{ccc}0& \eta \frac{v}{h}& 0\\ \eta \frac{v}{h}& 0& 0\\ 0& 0& 0\end{array}\right)}$

La fuerza por unidad de área

${\displaystyle \frac{F}{A}=\eta \frac{v}{h}}$

Esta relación lineal es el fundamento físico de los experimentos que miden la viscosidad de un fluido

Dos fluidos inmiscibles

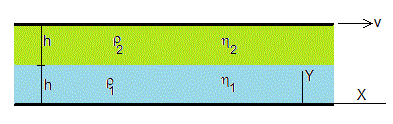
Consideremos dos fluidos inmiscibles (agua y aceite) de densidades ρ₁ y ρ₂ y viscosidades η₁ y η₂, respectivamente. Ambos fluidos tienen un espesor h

Para calcular las velocidades u_1x y u_2x de los dos fluidos a lo largo de eje X resolveremos las ecuaciones diferenciales

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{{\partial }^2{u}_{1x}}{\partial y^2}=0\\ \frac{{\partial }^2{u}_{2x}}{\partial y^2}=0\end{array}\\ \{\begin{array}{l}{u}_{1x}=a_{1}y+a_2\\ u_{2x}=b_{1}y+b_2\end{array}\end{array}}$

Las condiciones de contorno, determinan los cuatro coeficientes a₁, a₂, b₁, b₂

${\displaystyle \{\begin{array}{l}{u}_{2x}(2h)=v\\ u_{1x}(0)=0\end{array}}$

Las velocidades de los fluidos coinciden en y=h

${\displaystyle u_{2x}(h)=u_{1x}(h)}$

El esfuero viscoso τ_xy de un fluido sobre el otro coinciden en y=h

${\displaystyle \begin{array}{l}{\tau }_{xy}=\eta \left(\frac{\partial u_x}{\partial y}+\frac{\partial u_y}{\partial x}\right)=\eta \frac{\partial u_x}{\partial y}\\ {{\eta }_1\frac{\partial u_{1x}}{\partial y}|}_{y=h}={\eta }_2{\frac{\partial u_{2x}}{\partial y}|}_{y=h}\end{array}}$

El sistema de cuatro ecuaciones con cuatro incógnitas es

${\displaystyle \begin{array}{l}\{\begin{array}{l}{a}_2=0\\ v=b_1(2h)+b_2\\ a_{1}h=b_{1}h+b_2\\ {\eta }_1{a}_1={\eta }_2{b}_1\end{array}\\ a_1=\frac{v}{h}\frac{{\eta }_2}{{\eta }_1+{\eta }_2},b_1=\frac{v}{h}\frac{{\eta }_1}{{\eta }_1+{\eta }_2},b_2=v\frac{{\eta }_2-{\eta }_1}{{\eta }_1+{\eta }_2}\end{array}}$

El perfil de velocidades de los dos fluidos viene descrito por

${\displaystyle \{\begin{array}{l}{u}_{1x}=\frac{v}{\frac{{\eta }_1}{{\eta }_2}+1}\frac{y}{h},0\le y\le h\\ u_{2x}=\frac{v}{\frac{{\eta }_1}{{\eta }_2}+1}\left(\frac{{\eta }_1}{{\eta }_2}\left(\frac{y}{h}-1\right)+1\right),h\le y\le 2h\end{array}}$

Representamos el perfil de las velocidades de los dos fluidos, para η₁/η₂=0.5, 1.5.

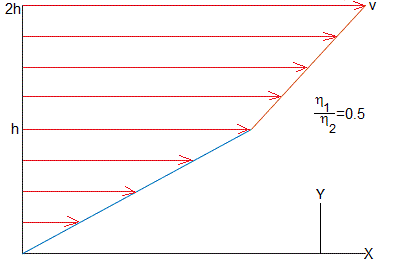
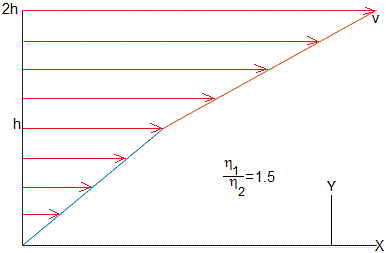
eta=0.5; %eta_1/eta_2
hold on
u1=@(y) y;
u2=@(y) eta*(y-1)+1;
fplot(u1,[0,1])
fplot(u2,[1,2])
hold off
xlabel('y')
ylabel('u_x/v')
title('Perfil de velocidades')
view (90,-90)

Además, se establece un gardiente de presión

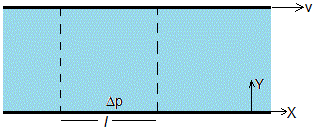
La placa superior se mueve con velocidad constante v y se establece un gradiente de presión

${\displaystyle \frac{\partial p}{\partial x}=\frac{p_2-p_1}{x_2-x_1}=\frac{\Delta p}{l}}$

El gradiente de presión es positivo, si p₂>p₁, o Δp>0. El fluido se mueve hacia la derecha, si p₂<p₁, si el gradiente de presión es negativo, Δp<0

El sistema de ecuaciones diferenciales en derivadas parciales se transforma en otro más simple

${\displaystyle \begin{array}{l}\frac{\partial u_x}{\partial x}=0\\ \{\begin{array}{l}-\frac{\partial p}{\partial x}+\eta \frac{{\partial }^2{u}_x}{\partial y^2}=0\\ -\frac{\partial p}{\partial y}-\rho g=0\end{array}\end{array}}$

La ecuación de continuidad nos indica que la componente u_x de la velocidad del fluido es función únicamente de y

Integrando u_x dos veces

${\displaystyle \begin{array}{l}\eta \frac{{\partial }^2{u}_x}{\partial y^2}=\frac{\Delta p}{l}\\ u_x=\frac{1}{2}\frac{\Delta p}{\eta l}{y}^2+c_{1}y+c_2\end{array}}$

Las constantes c₁ y c₂ se determinan a partir de las condiciones de contorno: u_x(0)=0, c₂=0. u_x(h)=v

${\displaystyle \begin{array}{l}v=\frac{1}{2}\frac{\Delta p}{\eta l}{h}^2+c_{1}h\\ c_1=\frac{v}{h}-\frac{1}{2}\frac{\Delta p}{\eta l}h\\ u_x=\frac{1}{2}\frac{\Delta p}{\eta l}{y}^2+\left(\frac{v}{h}-\frac{1}{2}\frac{\Delta p}{\eta l}h\right)y=\frac{v}{h}y-\frac{1}{2}\frac{\Delta p}{\eta l}\left(h-y\right)y\end{array}}$

El perfil de velocidades del fluido entre las dos placas es

En forma adimensional

${\displaystyle \frac{u_x}{v}=\frac{y}{h}-\frac{1}{2}\frac{\Delta p{h}^2}{\eta lv}\left(1-\frac{y}{h}\right)\frac{y}{h}}$

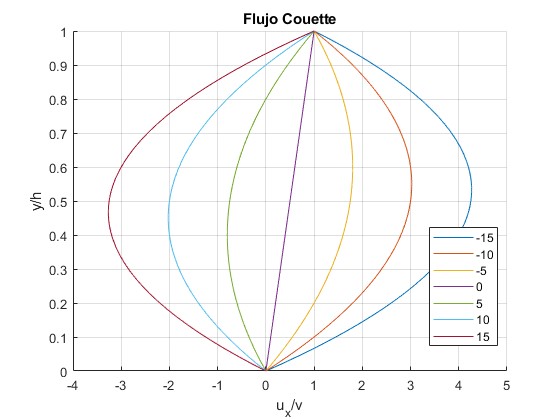
Representamos la función u_x/v en función de y/h para varios valores del parámetro

${\displaystyle k=\frac{1}{2}\frac{\Delta p{h}^2}{\eta lv}}$

hold on
for k=-15:5:15
    f=@(y) y-k*(1-y).*y;
    fplot(f,[0,1],'displayName',num2str(k))
end
hold off
grid on
xlabel('y/h')
ylabel('u_x/v')
legend('-DynamicLegend','location','best')
title('Flujo Couette')
view (90,-90)

El gasto

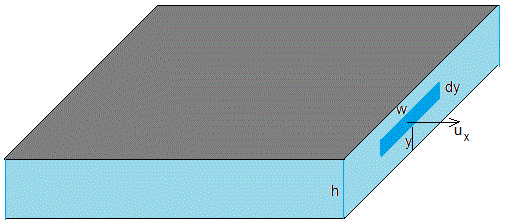
El volumen de fluido que atraviesa el área de longitud w y anchura dy (señalada en color azul en la figura) en la unidad de tiempo es u_x(w·dy). El flujo o gasto (m³/s) es

${\displaystyle G={\displaystyle \underset{0}{\overset{h}{\int }}{u}_x\left(wdy\right)}=vw{\displaystyle \underset{0}{\overset{h}{\int }}\left(\frac{y}{h}-k\left(1-\frac{y}{h}\right)\frac{y}{h}\right)dy}=v{w\left(\frac{1}{2}\frac{y^2}{h}-\frac{1}{2}k\frac{y^2}{h}+\frac{1}{3}k\frac{y^3}{h^2}\right)|}_0^h=whv\left(\frac{1}{2}-\frac{1}{6}k\right)}$

Para k=3, el gasto G es nulo

La placa superior no se mueve

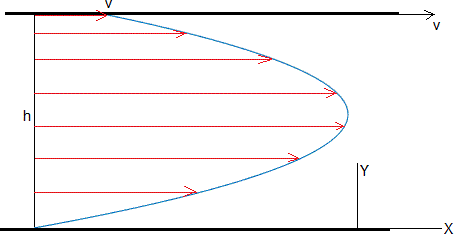
En el caso de que la placa superior no se mueva, v=0. El fluido se mueve bajo acción del gradiente de presión

${\displaystyle u_x=-\frac{1}{2}\frac{\Delta p}{\eta l}\left(h-y\right)y}$

El perfil de velocidades del fluido entre las dos placas es parabólico y se denomina flujo de Poiseuille

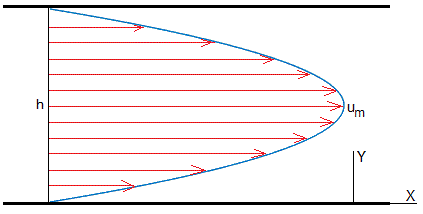
La máxima velocidad se produce para y=h/2

${\displaystyle u_m=-\frac{1}{8}\frac{\Delta p}{\eta l}{h}^2}$

Gasto

${\displaystyle G={\displaystyle \underset{0}{\overset{h}{\int }}{u}_x\left(wdy\right)}=-\frac{1}{2}\frac{\Delta p}{\eta l}w{\displaystyle \underset{0}{\overset{h}{\int }}\left(\left(h-y\right)y\right)dy}=-{\frac{1}{2}\frac{\Delta p}{\eta l}w\left(\frac{1}{2}h{y}^2-\frac{1}{3}{y}^3\right)|}_0^h=-\frac{1}{12}\frac{\Delta p}{\eta l}w{h}^3}$

Dos fluidos inmiscibles

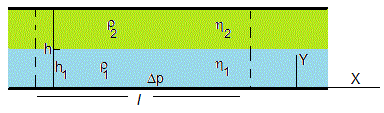
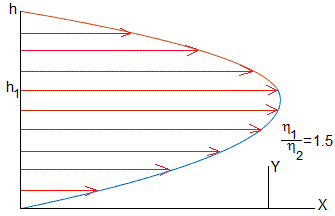
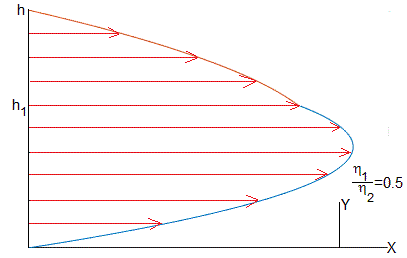
Consideremos dos fluidos inmiscibles (agua y aceite) de densidades ρ₁ y ρ₂ y viscosidades η₁ y η₂, respectivamente. El primer fluido tiene un espesor h₁ y el segundo un espesor h-h₁. Ambos fluidos se mueven a lo largo del eje X bajo la acción de un gradiente de presión Δp/l

Para calcular las velocidades u_1x y u_2x de los dos fluidos a lo largo de eje X, resolveremos las ecuaciones diferenciales

${\displaystyle \begin{array}{l}\{\begin{array}{l}{\eta }_1\frac{{\partial }^2{u}_{1x}}{\partial y^2}=\frac{\Delta p}{l}\\ {\eta }_2\frac{{\partial }^2{u}_{2x}}{\partial y^2}=\frac{\Delta p}{l}\end{array}\\ \{\begin{array}{l}{u}_{1x}=\frac{1}{2}\frac{\Delta p}{{\eta }_{1}l}{y}^2+a_{1}y+a_2\\ u_{2x}=\frac{1}{2}\frac{\Delta p}{{\eta }_{2}l}{y}^2+b_{1}y+b_2\end{array}\end{array}}$

Las condiciones de contorno, determinan los cuatro coeficientes a₁, a₂, b₁, b₂

${\displaystyle \{\begin{array}{l}{u}_{2x}(h)=0\\ u_{1x}(0)=0\end{array}}$

Las velocidades de los fluidos coinciden en y=h₁

${\displaystyle u_{2x}(h_1)=u_{1x}(h_1)}$

El esfuero viscoso τ_xy de un fluido sobre el otro coinciden en y=h₁

${\displaystyle \begin{array}{l}{\tau }_{xy}=\eta \frac{\partial u_x}{\partial y}\\ {{\eta }_1\frac{\partial u_{1x}}{\partial y}|}_{y=h_1}={\eta }_2{\frac{\partial u_{2x}}{\partial y}|}_{y=h_1}\end{array}}$

El sistema de cuatro ecuaciones con cuatro incógnitas es

${\displaystyle \begin{array}{l}\{\begin{array}{l}{a}_2=0\\ \frac{1}{2}\frac{\Delta p}{{\eta }_{2}l}{h}^2+b_{1}h+b_2=0\\ \frac{1}{2}\frac{\Delta p}{{\eta }_{1}l}{h}_1^2+a_1{h}_1=\frac{1}{2}\frac{\Delta p}{{\eta }_{2}l}{h}_1^2+b_1{h}_1+b_2\\ {\eta }_1\left(\frac{\Delta p}{{\eta }_{1}l}{h}_1+a_1\right)={\eta }_2\left(\frac{\Delta p}{{\eta }_{2}l}{h}_1+b_1\right)\end{array}\\ a_1=-\frac{1}{2}\frac{\Delta p}{l}\frac{h_1^2\left(\frac{1}{{\eta }_1}-\frac{1}{{\eta }_2}\right)+\frac{h^2}{{\eta }_2}}{h_1\left(1-\frac{{\eta }_1}{{\eta }_2}\right)+\frac{{\eta }_1}{{\eta }_2}h},b_1=\frac{{\eta }_1}{{\eta }_2}{a}_1\\ b_2=-\frac{1}{2}\frac{\Delta p}{{\eta }_{2}l}{h}^2-b_{1}h\end{array}}$

El perfil de velocidades de los dos fluidos viene descrito por

${\displaystyle \begin{array}{l}{u}_{1x}=\frac{1}{2}\frac{\Delta p}{l}\frac{h^2}{{\eta }_2}\left\{\frac{{\eta }_2}{{\eta }_1}\frac{y^2}{h^2}+\frac{{\left(\frac{h_1}{h}\right)}^2\left(1-\frac{{\eta }_2}{{\eta }_1}\right)-1}{\frac{h_1}{h}\left(1-\frac{{\eta }_1}{{\eta }_2}\right)+\frac{{\eta }_1}{{\eta }_2}}\frac{y}{h}\right\}\\ u_{2x}=\frac{1}{2}\frac{\Delta p}{l}\frac{h^2}{{\eta }_2}\left\{\left(\frac{y^2}{h^2}-1\right)-\frac{{\left(\frac{h_1}{h}\right)}^2\left(1-\frac{{\eta }_1}{{\eta }_2}\right)+\frac{{\eta }_1}{{\eta }_2}}{\frac{h_1}{h}\left(1-\frac{{\eta }_1}{{\eta }_2}\right)+\frac{{\eta }_1}{{\eta }_2}}\left(\frac{y}{h}-1\right)\right\}\end{array}}$

Representamos el perfil de las velocidades de los dos fluidos, el primero, de espesor h₁=0.6h, el segundo 0.4h, para η₁/η₂=0.5, 1.5.

eta=0.5; %eta_1/eta_2
h1=0.6; %h1/h
hold on
u1=@(y) -y.^2/eta-(h1^2*(1-1/eta)-1)*y/(h1*(1-eta)+eta);
u2=@(y) -(y.^2-1)+(h1^2*(1-eta)+eta)*(y-1)/(h1*(1-eta)+eta);
fplot(u1,[0,h1])
fplot(u2,[h1,1])
hold off
xlabel('y')
ylabel('u_x/v')
title('Perfil de velocidades')
view (90,-90)

Flujo a lo largo de un plano inclinado

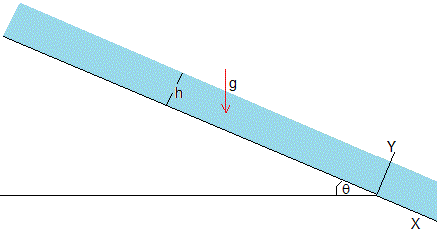
Un fluido incompresible fluye por un plano inclinado θ. En el estado estacionario, el espesor h de fluido es constante.

En este caso, probamos los efectos de la aceleración de la gravedad sobre el perfil de velocidades del fluido

La superficie libre el fluido está en contacto con el aire, que se considera un fluido perfecto a la presión p₀. Como la presión es uniforme en la superficie libre, la presión p en en el fluido no depende de x solamente de y

El flujo es paralelo al plano inclinado (ejeX) por lo que u_y=0

El sistema de ecuaciones diferenciales en derivadas parciales se transforma en otro más simple

${\displaystyle \begin{array}{l}\frac{\partial u_x}{\partial x}=0\\ \{\begin{array}{l}0={\rho }_{f}g\sin \theta +\eta \frac{{\partial }^2{u}_x}{\partial y^2}\\ 0=-\frac{\partial p}{\partial y}-{\rho }_{f}g\cos \theta \end{array}\end{array}}$

La ecuación de continuidad nos indica que la componente u_x de la velocidad del fluido es función únicamente de y

Integrando u_x dos veces

${\displaystyle \begin{array}{l}{\rho }_{f}g\sin \theta +\eta \frac{{\partial }^2{u}_x}{\partial y^2}=0\\ \frac{\partial u_x}{\partial y}=-\frac{{\rho }_{f}g\sin \theta }{\eta }y+c_1\\ u_x=-\frac{1}{2}\frac{{\rho }_{f}g\sin \theta }{\eta }{y}^2+c_{1}y+c_2\end{array}}$

Las constantes c₁ y c₂ se determinan a partir de las condiciones de contorno: u_x(0)=0, c₂=0. La otra condición es que en la superficie libre, el esfuerzo viscoso τ_xy=0

${\displaystyle \begin{array}{l}{\tau }_{xy}=\eta \left(\frac{\partial u_x}{\partial y}+\frac{\partial u_y}{\partial x}\right)=\eta \frac{\partial u_x}{\partial y}\\ {\frac{\partial u_x}{\partial y}|}_{x=h}=0\end{array}}$

Determinamos la constante c₁

${\displaystyle 0=-\frac{{\rho }_{f}g\sin \theta }{\eta }h+c_1}$

El resultado es

${\displaystyle u_x=\frac{{\rho }_{f}g\sin \theta }{2\eta }\left(2h-y\right)y}$

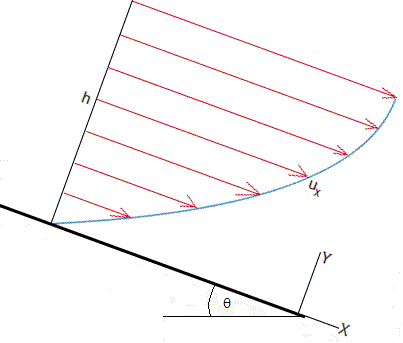
La velocidad máxima para y=h es

${\displaystyle u_m=\frac{{\rho }_{f}g\sin \theta }{2\eta }{h}^2}$

El volumen de fluido que atraviesa el área de longitud w y anchura dy en la unidad de tiempo es u_x(w·dy). El flujo o gasto (m³/s) es

${\displaystyle G={\displaystyle \underset{0}{\overset{h}{\int }}{u}_x\left(wdy\right)}=w{\displaystyle \underset{0}{\overset{h}{\int }}\left(\frac{{\rho }_{f}g\sin \theta }{2\eta }\left(2h-y\right)y\right)dy}=w\frac{{\rho }_{f}g\sin \theta }{2\eta }{\left(h{y}^2-\frac{y^3}{3}\right)|}_0^h=\frac{{\rho }_{f}g\sin \theta }{3\eta }w{h}^3}$

Dos fluidos inmiscibles

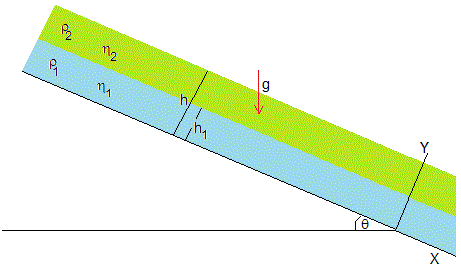
Consideremos dos fluidos inmiscibles (agua y aceite) de densidades ρ₁ y ρ₂ y viscosidades η₁ y η₂, respectivamente. El primer fluido tiene un espesor h₁ y el segundo un espesor h-h₁. Ambos fluidos se mueven a lo largo del eje X bajo la acción de la componenente del peso

Para calcular las velocidades u_1x y u_2x de los dos fluidos a lo largo de eje X, resolveremos las ecuaciones diferenciales

${\displaystyle \begin{array}{l}\{\begin{array}{l}{\eta }_1\frac{{\partial }^2{u}_{1x}}{\partial y^2}=-{\rho }_{1}g\sin \theta \\ {\eta }_2\frac{{\partial }^2{u}_{2x}}{\partial y^2}=-{\rho }_{2}g\sin \theta \end{array}\\ \{\begin{array}{l}{u}_{1x}=-\frac{1}{2}\frac{{\rho }_{1}g\sin \theta }{{\eta }_1}{y}^2+a_{1}y+a_2\\ u_{2x}=-\frac{1}{2}\frac{{\rho }_{2}g\sin \theta }{{\eta }_2}{y}^2+b_{1}y+b_2\end{array}\end{array}}$

Las condiciones de contorno son

• En el plano inclinado y=0

${\displaystyle u_{1x}(0)=0}$

• En la superficie de separación entre dos dos fluidos, y=h₁

La velocidad de ambos líquidos es la misma

${\displaystyle u_{1x}(h_1)=u_{2x}(h_1)}$

El esfuero viscoso τ_xy de un fluido sobre el otro coinciden en y=h₁

${\displaystyle \begin{array}{l}{\tau }_{xy}=\eta \frac{\partial u_x}{\partial y}\\ {{\eta }_1\frac{\partial u_{1x}}{\partial y}|}_{y=h_1}={\eta }_2{\frac{\partial u_{2x}}{\partial y}|}_{y=h_1}\end{array}}$

• En la superficie libre y=h, el esfuerzo viscoso τ_xy=0

${\displaystyle {{\eta }_2\frac{\partial u_{2x}}{\partial y}|}_{x=h}=0}$

Tenemos un sistema de cuatro ecuaciones con cuatro incógnitas, cuya solución es

${\displaystyle \begin{array}{l}{a}_2=0\\ b_1=\frac{{\rho }_{2}g\sin \theta }{{\eta }_2}h\\ a_1=\frac{{\rho }_{2}g\sin \theta \left(h-h_1\right)+{\rho }_{1}g\sin \theta ·h_1}{{\eta }_1}\\ b_2=-\frac{{\rho }_{1}g\sin \theta }{2{\eta }_1}{h}_1^2+a_1{h}_1+\frac{{\rho }_{2}g\sin \theta }{2{\eta }_2}{h}_1^2-b_1{h}_1\end{array}}$

Expresamos el perfil de velocidades en unidades adimensionales dividiendo u_1x y u_2x entre $u_m=\frac{{\rho }_{2}g\sin \theta }{2{\eta }_2}{h}^2$

El resultado es

${\displaystyle \begin{array}{l}\frac{u_{1x}}{u_m}=-\frac{{\rho }_1}{{\rho }_2}\frac{{\eta }_2}{{\eta }_1}\frac{y^2}{h^2}+2\frac{{\eta }_2}{{\eta }_1}\left(1+\left(\frac{{\rho }_1}{{\rho }_2}-1\right)\frac{h_1}{h}\right)\frac{y}{h}\\ \frac{u_{2x}}{u_m}=-\frac{y^2}{h^2}+2\frac{y}{h}+2\left(\frac{{\eta }_2}{{\eta }_1}-1\right)\frac{h_1}{h}+\left(1+\frac{{\rho }_1}{{\rho }_2}\frac{{\eta }_2}{{\eta }_1}-2\frac{{\eta }_2}{{\eta }_1}\right)\frac{h_1^2}{h^2}\end{array}}$

Representamos el perfil de las velocidades de los dos fluidos, el primero, de espesor h₁=0.6h, el segundo 0.4h, para el cociente de viscosidades η₂/η₁=0.2 y para el cociente de densidades ρ₁/ρ₂=1.25.

eta=0.2; %eta_2/eta_1
rho=1.25; %rho_1/rho_2
h1=0.6; %h1/h
hold on
u1=@(y) -rho*eta*y.^2+2*eta*(1-h1+rho*h1)*y;
fplot(u1, [0,h1])
u2=@(y) -y.^2+2*y+2*(eta-1)*h1+(1+rho*eta-2*eta)*h1^2;
fplot(u2, [h1,1])
hold off
grid on
xlabel('y/h')
xlabel('u_x/u_m')
title('Perfil de velocidades')
view (90,-90)

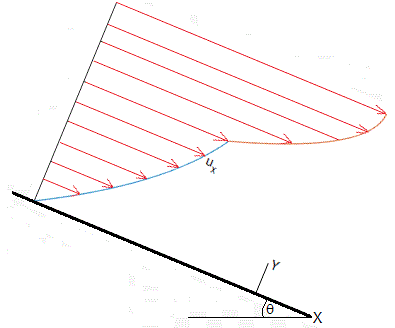
Flujo entre dos placas porosas, planas y paralelas

Hemos estudiado el caso de un fluido ente dos placas planas y paralelas separadas una distancia h, sometido a un gradiente de presión Δp/l. El perfil u_x(y) de la velocidad del fluido tiene forma parabólica

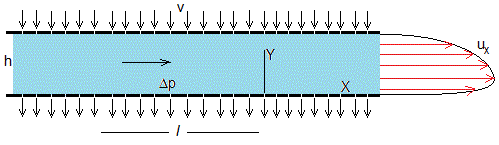
Supongamos que las placas son porosas y el fluido que entra por la placa superior con velocidad v sale por la placa inferior con la misma velocidad. Vamos a determinar el perfil u_x(y) de la velocidad del fluido

En este caso u_y≠0, tenemos que resolver la ecuación diferencial

${\displaystyle {\rho }_f{u}_y\frac{\partial u_x}{\partial y}=-\frac{\Delta p}{l}+\eta \frac{{\partial }^2{u}_x}{\partial y^2}}$

Con las condiciones de contorno:

• u_y=-v en y=0 y en y=h

• u_x=0 en y=0 y en y=h

La ecuación de continuidad nos dice que

${\displaystyle \frac{\partial u_y}{\partial y}=0}$

lo que indica que u_y=cte, u_y=-v.

Integramos la ecuación diferencial

${\displaystyle \upsilon \frac{{\partial }^2{u}_x}{\partial y^2}+v\frac{\partial u_x}{\partial y}=\frac{1}{{\rho }_f}\frac{\Delta p}{l},\upsilon =\frac{\eta }{{\rho }_f}}$

La solución de la homogénea es

${\displaystyle u_x=c_1+c_2\exp \left(-\frac{v}{\upsilon }y\right)}$

Como la constante c₁ es solución de la homogénea, la solución particular es de la forma c₃y. Introduciendo en la ecuación diferencial determinamos el coeficiente c₃

${\displaystyle \begin{array}{l}v{c}_3=\frac{1}{{\rho }_f}\frac{\Delta p}{l}\\ c_3=\frac{1}{{\rho }_{f}v}\frac{\Delta p}{l}\end{array}}$

La solución completa de la ecuación diferencial es la suma de la particular y al homogénea

${\displaystyle u_x=c_1+c_2\exp \left(-\frac{v}{\upsilon }y\right)+\frac{1}{{\rho }_{f}v}\frac{\Delta p}{l}y}$

Los coeficientes c₁ y c₂ se determinan a partir de las condiciones de contorno en y=0 y en y=h

${\displaystyle \begin{array}{l}\{\begin{array}{l}0=c_1+c_2\\ 0=c_1+c_2\exp \left(-\frac{v}{\upsilon }h\right)+\frac{1}{{\rho }_{f}v}\frac{\Delta p}{l}h\end{array}\\ c_2=\frac{\frac{1}{{\rho }_{f}v}\frac{\Delta p}{l}h}{1-\exp \left(-\frac{v}{\upsilon }h\right)},c_1=-c_2\end{array}}$

El perfil de velocidades es

${\displaystyle \begin{array}{l}{u}_x=\frac{1}{{\rho }_{f}v}\frac{\Delta p}{l}\left\{y-h\frac{1-\exp \left(-\frac{v}{\upsilon }y\right)}{1-\exp \left(-\frac{v}{\upsilon }h\right)}\right\}\\ u_x=\frac{1}{{\rho }_{f}v}\frac{\Delta p}{l}h\left\{\frac{y}{h}-\frac{1-\exp \left(-k\frac{y}{h}\right)}{1-\exp \left(-k\right)}\right\},k=\frac{{\rho }_{f}vh}{\eta }\end{array}}$

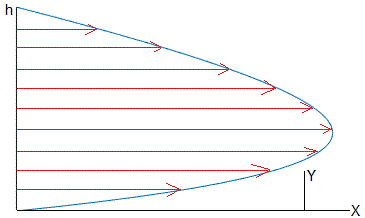
Cuando las placas no son porosas, calculamos la velocidad máxima del fluido sometido al gradiente de presión

${\displaystyle u_m=-\frac{1}{8}\frac{\Delta p}{\eta l}{h}^2}$

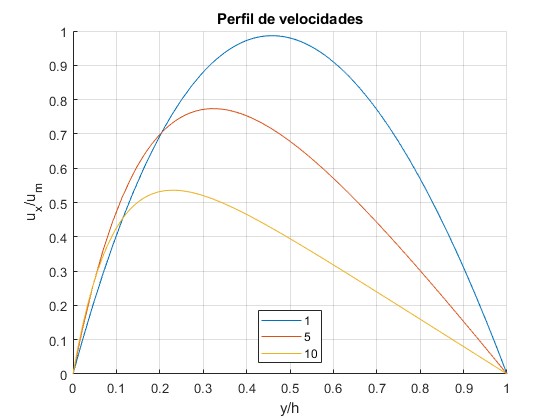
Expresamos el perfil de velocidades del fluido de forma adimensional dividiendo u_x(y) entre u_m

${\displaystyle \frac{u_x}{-\frac{1}{8}\frac{\Delta p}{\eta l}{h}^2}=\frac{8}{k}\left\{\frac{1-\exp \left(-k\frac{y}{h}\right)}{1-\exp \left(-k\right)}-\frac{y}{h}\right\}}$

Representamos el perfil de velocidades u_x/u_m en función de y/h para k= 1, 5, 10

hold on
for k=[1, 5, 10]
    f=@(y) 8*((1-exp(-k*y))/(1-exp(-k))-y)/k;
    fplot(f,[0,1],'displayName',num2str(k))
end
hold off
grid on
legend('-DynamicLegend','location','best')
xlabel('y/h')
ylabel('u_x/u_m')
title('Perfil de velocidades')

Gasto

${\displaystyle \begin{array}{l}G={\displaystyle \underset{0}{\overset{h}{\int }}{u}_x\left(wdy\right)}=w{\displaystyle \underset{0}{\overset{h}{\int }}\left(\frac{1}{{\rho }_{f}v}\frac{\Delta p}{l}h\left\{\frac{y}{h}-\frac{1-\exp \left(-k\frac{y}{h}\right)}{1-\exp \left(-k\right)}\right\}\right)dy}=\\ w\frac{1}{{\rho }_{f}v}\frac{\Delta p}{l}h{\left\{\frac{1}{2}\frac{y^2}{h}-\frac{1}{1-\exp \left(-k\right)}\left(y+\frac{h}{k}\exp \left(-k\frac{y}{h}\right)\right)\right\}|}_0^h=\\ w\frac{1}{{\rho }_{f}v}\frac{\Delta p}{l}{h}^2\left\{\frac{1}{2}+\frac{\frac{1}{k}\left(1-\exp \left(-k\right)\right)-1}{1-\exp \left(-k\right)}\right\}\end{array}}$

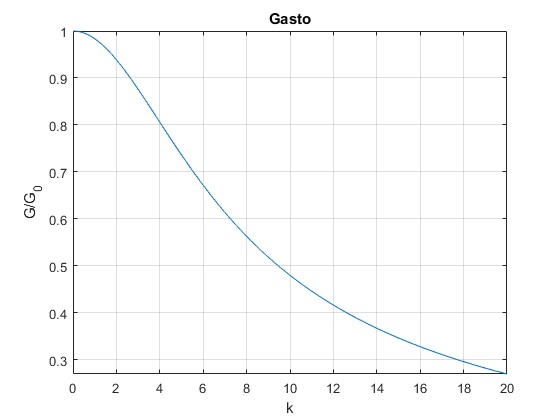
Cuando las placas no son porosas, calculamos el gasto del fluido sometido al gradiente de presión

${\displaystyle G_0=-\frac{1}{12}\frac{\Delta p}{\eta l}w{h}^3}$

Dividimos el gasto G entre G₀

${\displaystyle \frac{G}{G_0}=\frac{\frac{1}{{\rho }_{f}v}\left\{\frac{1}{2}+\frac{\frac{1}{k}\left(1-\exp \left(-k\right)\right)-1}{1-\exp \left(-k\right)}\right\}}{-\frac{1}{12}\frac{h}{\eta }}=-\frac{12}{k}\left\{\frac{1}{2}+\frac{\frac{1}{k}\left(1-\exp \left(-k\right)\right)-1}{1-\exp \left(-k\right)}\right\}}$

Representamos G/G₀ en función de k

f=@(k) -12*(1/2+((1-exp(-k))./k-1)./(1-exp(-k)))./k;
fplot(f,[0,20])
grid on
ylabel('G/G_0')
xlabel('k')
title('Gasto')

Referencias

Simon Schneiderbauer, Michael Krieger. What do Navier-Stokes equations mean?. Eur. J. Phys. 35 (2014), 015020

Michel O. Deville. An Introduction to the Mechanics of Incompressible Fluids. Springer (2022), pp. 51-57

Charles R. (Chuck) Smith. Introduction to Graduate Fluid Mechanics. Fourth Edition. Self-Published, 2023. pp. 131-136, 139-149