Presión en el interior de un globo

Cuando un globo sin deformar de radio r₀ se infla hasta alcanzar un radio r>r₀, la superficie del globo adquiere una energía elástica debido a la deformación. La expresión de la energía elástica cuando el globo se encuentra en un ambiente a la temperatura T es

${\displaystyle U=4\pi r_0^{2}kRT\left(2\frac{r^2}{r_0^2}+\frac{r_0^4}{r^4}-3\right)}$

donde k es una constante en unidades mol/m², R=8.3143 J/(K·mol) es la constante de los gases .

El trabajo necesario para incrementar el radio del globo de r a r+dr bajo la acción de una diferencia de presión ΔP entre el interior P_int y el exterior P_ext es el producto de la diferencia de presión ΔP por el incremento de volumen $dV=d\left(\frac{4}{3}\pi r^3\right)=4\pi r^{2}dr$

dW=4πr²ΔP·dr

Este trabajo se invierte en incrementar la energía elástica de la superficie del globo.

${\displaystyle \begin{array}{l}dW=\left(\frac{dU}{dr}\right)dr=16\pi kRT\left(r-\frac{r_0^6}{r^5}\right)dr\\ 4\pi r^2\Delta Pdr=16\pi kRT\left(r-\frac{r_0^6}{r^5}\right)dr\\ \Delta P=\frac{4kRT}{r_0}\left(\frac{r_0}{r}-\frac{r_0^7}{r^7}\right)\\ P_{\mathrm{int}}-P_{ext}=\frac{4kRT}{r_0}\left(\frac{1}{\lambda }-\frac{1}{{\lambda }^7}\right)\lambda =\frac{r}{r_0}\end{array}}$

En la figura se muestra la gráfica de la función

${\displaystyle f(\lambda )=\left(\frac{1}{\lambda }-\frac{1}{{\lambda }^7}\right)}$

>> syms x;
>> y=1/x-1/x^7;
>> ezplot(y,[0.5,5])
>> grid on
>> xlabel('\lambda')
>> ylabel('y')
>> title('Presión en el interior de un globo')

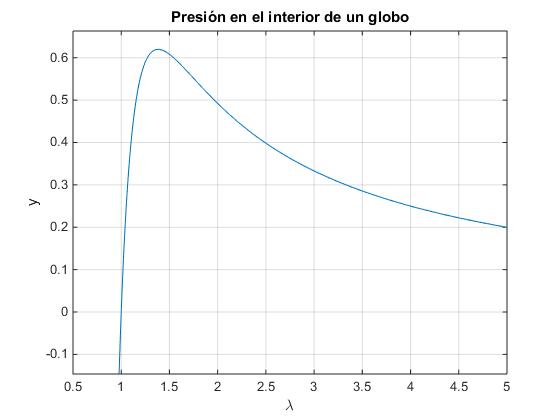
La diferencia de presión se incrementa rápidamente con el cociente λ=r/r₀, alcanza un máximo y luego, disminuye como 1/λ para grandes valores de λ.

Obtenemos el extremo de la función, igualando la derivada de la función f(λ) a cero

${\displaystyle \begin{array}{l}-\frac{1}{{\lambda }^2}+7\frac{1}{{\lambda }^8}=0{\lambda }^6=7\\ \lambda =1.383\end{array}}$

Inflando el globo

Inicialmente el globo está en un ambiente a la presión atmosférica P_ext=P₀ y a la temperatura T₀, contiene n₀ moles de gas Helio y su radio es r₀. La presión del gas en el interior del globo es P₀. La ecuación de los gases ideales es

${\displaystyle P_0\frac{4}{3}\pi r_0^3=n_{0}R{T}_0}$

Conectamos el globo a una bombona de gas que le suministra Δn moles. El número de moles de gas en el interior del globo es n=n₀+Δn. La presión en el interior del globo de forma esférica de radio r es P.

De la ecuación de los gases ideales tenemos que

${\displaystyle \begin{array}{l}P\frac{4}{3}\pi r^3=nR{T}_0=\frac{n}{n_0}{P}_0\frac{4}{3}\pi r_0^3\\ P{\lambda }^3=P_0\frac{n}{n_0}\end{array}}$

Como la diferencia de presión entre el interior y exterior de un globo es

${\displaystyle P-P_0=\frac{4kR{T}_0}{r_0}\left(\frac{1}{\lambda }-\frac{1}{{\lambda }^7}\right)}$

Combinando estas dos ecuaciones, calculamos el radio λ=r/r₀ del globo

${\displaystyle \frac{n}{n_0}\frac{1}{{\lambda }^3}-1=\frac{16\pi k{r}_0^2}{3n_0}\left(\frac{1}{\lambda }-\frac{1}{{\lambda }^7}\right)}$

la raíz real del polinomio

${\displaystyle {\lambda }^7+b{\lambda }^6-a{\lambda }^4-b=0a=\frac{n}{n_0}b=\frac{16\pi k{r}_0^2}{3n_0}}$

Una vez calculado λ, por algún procedimiento numérico, la diferencia de presión entre el interior y exterior del globo es

${\displaystyle \Delta P=P_0\frac{16\pi k{r}_0^2}{3n_0}\left(\frac{1}{\lambda }-\frac{1}{{\lambda }^7}\right)}$

Ejemplo.

• Presión atmosférica, P₀=101300 Pa
• Temperatura ambiente, T₀=30º=303 K
• Radio inicial del globo r₀=42 cm
• Se ha fijado el valor de la constante k=0.46235

Número de moles iniciales de gas

${\displaystyle P_0\frac{4}{3}\pi r_0^3=n_{0}R{T}_0{n}_0=12.5}$

Cada vez que se conecta la bomba de inyección, el gas contenido en el globo se incrementa en 5 moles.

Para calcular el nuevo radio del globo hay que resolver la ecuación

${\displaystyle \begin{array}{l}{\lambda }^7+b{\lambda }^6-a{\lambda }^4-b=0\\ a=\frac{12.5+i·5}{12.5}b=\frac{16\pi ·0.4623·{0.42}^2}{3·12.5}=0.10931i=\mathrm{1,2,3...}\\ \Delta P=101300·0.10931\left(\frac{1}{\lambda }-\frac{1}{{\lambda }^7}\right)=11073.1\left(\frac{1}{\lambda }-\frac{1}{{\lambda }^7}\right)\text{Pa}\end{array}}$

por algún procedimiento numérico y luego, calcularemos la diferencia de presión ΔP entre el interior y el exterior del globo.

k=0.46235;
r0=0.42;  %radio inicial
%moles iniciales de gas a presión atmosférica y temperatura ambiente.
n0=101300*4*pi*r0^3/(3*8.3143*303); 
b=16*pi*k*r0^2/(3*n0);
dn=5; %incremento del número de moles
for i=1:5;
    a=(n0+i*dn)/n0;
    f=@(x) x^7+b*x^6-a*x^4-b;
    x0=fzero(f,1.5); %resuelve 
    h=101300*b*(1/x0-1/x0^7)/(10*2*9.8) %presión en cm de agua
end

Obtenemos la presión en cm de agua, multiplicando h por dos, tal como vemos en la simulación más abajo

h =   22.8014
h =   31.0049
h =   34.0267
h =   34.9765
h =   35.0266

Actividades

Se pulsa el botón titulado Nuevo

Se pulsa el botón titulado Empieza

Se inyectan 5 moles de gas en el globo

El programa interactivo calcula el radio r del globo en cm y la diferencia de presión ΔP entre el interior y el exterior del globo en Pa. El manómetro mide la diferencia de presión en cm de agua. Por ejemplo, una diferencia de presión de 4473.3 Pa equivale a

${\displaystyle \frac{\Delta P}{\rho g}=\frac{4473.3}{1000·9.8}=0.4564\text{m}=2·22.8\text{cm}}$

Se vuelve a pulsar el botón titulado Empieza y se infla el globo con otros 5 moles de gas y así, sucesivamente.

Un globo que asciende

El globo de forma esférica se llena con n moles de gas Helio a nivel del mar donde la presión es P₀ y la temperatura T₀. Si P_int es la presión en el interior del globo

${\displaystyle P_{\mathrm{int}}\frac{4}{3}\pi r^3=nR{T}_0}$

La diferencia de presión entre el interior y el exterior del globo es

${\displaystyle P_{\mathrm{int}}-P_0=\frac{4kR{T}_0}{r_0}\left(\frac{1}{\lambda }-\frac{1}{{\lambda }^7}\right)\lambda =\frac{r}{r_0}}$

El radio del globo a nivel del mar es la raíz de la ecuación

${\displaystyle {\lambda }^7+b{\lambda }^6-a{\lambda }^4-b=0a=\frac{n}{n_0}b=\frac{16\pi k{r}_0^2}{3n_0}}$

Variación de la presión con la altura en una atmósfera lineal

Supondremos que la temperatura T disminuye linealmente con la altura y.

${\displaystyle T=T_0\left(1-\frac{y}{y_0}\right)}$

La variación de la presión con la altura se deduce a partir de la ecuación fundamental de la estática de fluidos

dP=-ρg·dy

junto a la ecuación de los gases ideales

${\displaystyle PV=\frac{m}{M_A}RTP=\frac{\rho }{M_A}RT}$

donde M_A=0.0289 kg/mol es el masa molecular del aire.

${\displaystyle \begin{array}{l}dP=-P\frac{M_{A}g{y}_0}{R{T}_0}\frac{1}{y_0-y}dy\\ {\displaystyle \underset{P_0}{\overset{P}{\int }}\frac{dP}{P}}=-\frac{M_{A}g{y}_0}{R{T}_0}{\displaystyle \underset{0}{\overset{y}{\int }}\frac{1}{y_0-y}dy}\\ \ln \frac{P}{P_0}=\eta \left(\ln \left(y_0-y\right)-\ln y_0\right)\eta =\frac{M_{A}g{y}_0}{R{T}_0}\\ P=P_0{\left(1-\frac{y}{y_0}\right)}^{\eta }\end{array}}$

• M_A=0.0289 kg/mol es el masa molecular del aire.
• R=8.3143 J/(K·mol) es la constante de los gases .
• Para ajustar la dependencia lineal de la temperatura T con la altura y un determinado día del año, se toma T₀=303 K a nivel del mar e y₀=49 km=49000 m

y0=49000;
T0=273+30; %kelvin
eta=0.0289*9.8*y0/(8.3143*T0);
y=0:500:49000;
p=(1-y/y0).^eta;
plot(y/1000,p)
grid on
xlabel('y (km)')
ylabel('P/P_0')
title('Modelo de atmósfera')

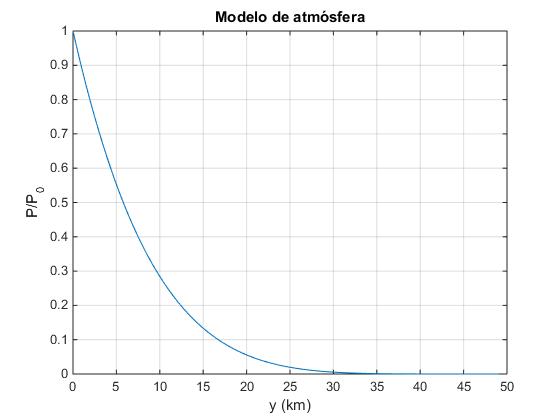
A medida que el globo asciende la diferencia de presión entre el interior y el exterior aumenta y por tanto, el radio del globo cambia.

A una altura y la presión es P y la temperatura es T. Para calcular el nuevo radio del globo utilizamos ecuaciones similares a las empleadas para calcular el radio del globo a nivel del mar.

${\displaystyle \begin{array}{l}{P}_{\mathrm{int}}\frac{4}{3}\pi r^3=nRT\\ P_{\mathrm{int}}-P=\frac{4kRT}{r_0}\left(\frac{1}{\lambda }-\frac{1}{{\lambda }^7}\right)\lambda =\frac{r}{r_0}\end{array}}$

Obtenemos la ecuación

${\displaystyle \begin{array}{l}\frac{3nR{T}_0\left(1-\frac{y}{y_0}\right)}{4\pi r^3}-P_0{\left(1-\frac{y}{y_0}\right)}^{\eta }=\frac{4kR{T}_0\left(1-\frac{y}{y_0}\right)}{r_0}\left(\frac{1}{\lambda }-\frac{1}{{\lambda }^7}\right)\\ \frac{n}{n_0}\frac{P_0}{{\lambda }^3}\left(1-\frac{y}{y_0}\right)-P_0{\left(1-\frac{y}{y_0}\right)}^{\eta }=\frac{16\pi k{P}_0{r}_0^2}{3n_0}\left(1-\frac{y}{y_0}\right)\left(\frac{1}{\lambda }-\frac{1}{{\lambda }^7}\right)\\ \frac{n}{n_0}\frac{1}{{\lambda }^3}-{\left(1-\frac{y}{y_0}\right)}^{\eta -1}=\frac{16\pi k{r}_0^2}{3n_0}\left(\frac{1}{\lambda }-\frac{1}{{\lambda }^7}\right)\\ {\left(1-\frac{y}{y_0}\right)}^{\eta -1}{\lambda }^7+b{\lambda }^6-a{\lambda }^4-b=0a=\frac{n}{n_0}b=\frac{16\pi k{r}_0^2}{3n_0}\end{array}}$

Resolviendo esta ecuación obtenemos el radio r del globo o λ, a una altura y.

Cuando y=0 al nivel del mar obtenemos la ecuación de la sección anterior.

• M_A=0.0289 kg/mol es el masa molecular del aire.
• R=8.3143 J/(K·mol) es la constante de los gases .
• Se ha fijado el valor de la constante k=0.46235
• Tomamos T₀=303 K a nivel del mar e y₀=49 km=49000 m
• Presión atmosférica a nivel del mar (y=0), P₀=101300 Pa
• Radio inicial del globo, r₀=42 cm
• Se llena el globo con 45 moles de He, queremos calcular el radio del globo a la altura y=1000 m

k=0.46235;
r0=0.42;  %radio inicial
n0=101300*4*pi*r0^3/(3*8.3143*303); %moles iniciales de gas
b=16*pi*k*r0^2/(3*n0);
y0=49000;
eta=0.0289*9.8*y0/(8.3143*303);
n=45; %número de moles
a=n/n0;
y=1000;  %altura del globo
c=(1-y/y0)^eta;
f=@(x) c*x^7+b*x^6-a*x^4-b;
r=fzero(f,1.5)*r0 %radio del globo con n moles

r =    0.6533

Equilibrio

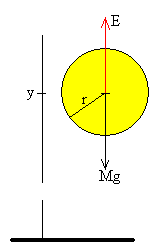
Supongamos que la masa del globo, incluyendo el gas y el lastre es M.

El globo detiene su ascensión cuando el peso se equilibra con el empuje.

El empuje es el peso del aire desalojado por el globo

${\displaystyle \begin{array}{l}E={\rho }_{aire}g\frac{4}{3}\pi r^3=\frac{M_{A}P}{RT}g\frac{4}{3}\pi r^3=\\ \frac{M_A{P}_0}{R{T}_0}{\left(1-\frac{y}{y_0}\right)}^{\eta -1}g\frac{4}{3}\pi r^3\\ E=M_A{n}_{0}g{\lambda }^3{\left(1-\frac{y}{y_0}\right)}^{\eta -1}\end{array}}$

En el equilibrio el peso es igual al empuje, Mg=E.

Combinado la ecuación que obtiene el radio del globo a una altura y con la ecuación de equilibrio a dicha altura.

${\displaystyle \begin{array}{l}M=M_A{n}_0\frac{b+a{\lambda }^4-b{\lambda }^6}{{\lambda }^7}\\ b{\lambda }^6+\left(\frac{M}{M_A{n}_0}-a\right){\lambda }^4-b=0\\ x^3+\frac{1}{b}\left(\frac{M}{M_A{n}_0}-a\right)x^2-1=0x={\lambda }^2\end{array}}$

Una vez obtenido λ=r/r₀, se despeja la altura máxima y en la primera ecuación.

Ejemplo:

• Presión atmosférica a nivel del mar (y=0), P₀=101300 Pa
• Radio inicial del globo, r₀=42 cm
• Se ha fijado el valor de la constante k=0.46235

Número de moles iniciales de gas

${\displaystyle P_0\frac{4}{3}\pi r_0^3=n_{0}R{T}_0{n}_0=12.5}$

• Se llena el globo con n=45 moles de gas Helio
• El peso del globo incluyendo el gas y el lastre es de M=1.12 kg
• M_A=0.0289 kg/mol es el masa molecular del aire.
• Tomamos T₀=303 K a nivel del mar e y₀=49 km=49000 m

Se suelta el globo. Calcular la altura máxima que alcanza

Tenemos que resolver la ecuación cúbica

${\displaystyle x^3+\frac{1}{b}\left(\frac{M}{M_A{n}_0}-a\right)x^2-1=0x={\lambda }^{2}a=\frac{n}{n_0}b=\frac{16\pi k{r}_0^2}{3n_0}}$

Con los datos suministrados,

x³-4.57047x²-1=0

esta ecuación tiene una raíz real y dos complejas conjugadas. Utilizando la calculadora para realizar las operaciones indicadas en la página titulada “Raíces de una ecuación cúbica” obtenemos la solución real x=4.6174, o bien, λ=2.1488.

En el apartado anterior, resolvimos el problema, dada la altura y calcular el radio del globo. Ahora resolvemos el problema inverso, dado el radio o λ calcular la altura y en la que el globo permanece en equilibrio

${\displaystyle {\left(1-\frac{y}{y_0}\right)}^{\eta -1}=\frac{b+a{\lambda }^4-b{\lambda }^6}{{\lambda }^7}\eta =\frac{M_{A}g{y}_0}{R{T}_0}}$

obtenemos y=11143 m

k=0.46235;
r0=0.42;  %radio inicial
n0=101300*4*pi*r0^3/(3*8.3143*303); %moles iniciales de gas
b=16*pi*k*r0^2/(3*n0);
y0=49000;
eta=0.0289*9.8*y0/(8.3143*303);
n=45; %número de moles
a=n/n0;
M=1.12;  %masa del globo
c=M/(0.0289*n0);
f=@(x) x^3+(c-a)*x^2/b-1;
lambda=sqrt(fzero(f,1.5))
%altura de equilibrio
y=y0-((b+a*lambda^4-b*lambda^6)/lambda^7)^(1/(eta-1))*y0

lambda =    2.1488
y =  1.1128e+04

Movimiento del globo desde el suelo hasta alcanzar la altura de equilibrio

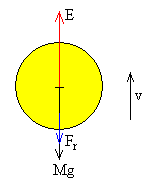
Las fuerzas sobre el globo son:

• El peso, Mg
• El empuje, E
• La fuerza de rozamiento F_r proporcional al cuadrado de la velocidad.

Supondremos que en todo momento las tres fuerzas se equilibran, el tiempo que tarda en alcanzar la velocidad límite es muy pequeño partiendo de una velocidad muy próxima.

Supondremos que la fuerza de rozamiento es proporcional al cuadrado de la velocidad, como en el caso del paracaidas. La constante de proporcionalidad de la fuerza de rozamiento es

${\displaystyle \frac{\rho A\delta }{2}}$

•  ρ es la densidad del aire que cambia con la altura y.
• A es el área de la sección transversal frontal expuesta al aire, para una esfera A=πr²
• δ es un coeficiente que depende de la forma del objeto, para una esfera δ=0.4

La ecuación del movimiento es

E-Mg-F_r=0

${\displaystyle \begin{array}{l}{M}_A{n}_{0}g{\lambda }^3{\left(1-\frac{y}{y_0}\right)}^{\eta -1}-Mg=0.2\frac{M_A{P}_0}{R{T}_0}{\left(1-\frac{y}{y_0}\right)}^{\eta -1}\pi r^2{v}^2\\ M_A{n}_{0}g{\lambda }^3{\left(1-\frac{y}{y_0}\right)}^{\eta -1}-Mg=0.3\frac{M_A{n}_0}{2r_0}{\left(1-\frac{y}{y_0}\right)}^{\eta -1}{\lambda }^2{v}^2\end{array}}$

Hay que resolver la ecuación diferencial de primer orden, con la condición inicial siguiente: en el instante t=0, y=0, parte del nivel del mar.

${\displaystyle \frac{dy}{dt}=\sqrt{\frac{20}{3}g{r}_0\left\{\lambda -\frac{M}{M_A{n}_0}\frac{1}{{\lambda }^2}{\left(1-\frac{y}{y_0}\right)}^{1-\eta }\right\}}}$

Para cada valor de y hay que calcular el radio r del globo o bien, el cociente λ=r/r₀ resolviendo la ecuación.

${\displaystyle {\left(1-\frac{y}{y_0}\right)}^{\eta -1}{\lambda }^7+b{\lambda }^6-a{\lambda }^4-b=0a=\frac{n}{n_0}b=\frac{16\pi k{r}_0^2}{3n_0}\eta =\frac{M_{A}g{y}_0}{R{T}_0}}$

Ejemplo:

• Se llena el globo con n=45 moles de gas Helio

Calcular la velocidad inicial del globo, cuando y=0.

Con el programa interactivo de la sección anterior, calculamos el radio inicial del globo a nivel del mar.

λ=1.50, r=63.0 cm

${\displaystyle v=\sqrt{\frac{20}{3}9.8·0.42\left\{1.5-\frac{1.12}{0.0289·12.5}\frac{1}{{1.5}^2}\right\}}=1.83\text{m/s}}$

Representamos la velocidad del globo dy/dt en función de la altura y del globo hasta que alcanza la altura de equilibrio. Completamos el script anterior, con los mismos datos:

• M_A=0.0289 kg/mol es el masa molecular del aire.
• R=8.3143 J/(K·mol) es la constante de los gases .
• Se ha fijado el valor de la constante k=0.46235
• Tomamos T₀=303 K a nivel del mar e y₀=49 km=49000 m
• Presión atmosférica a nivel del mar (y=0), P₀=101300 Pa
• Radio inicial del globo, r₀=42 cm
• Se llena el globo con 45 moles de He

k=0.46235;
r0=0.42;  %radio inicial
n0=101300*4*pi*r0^3/(3*8.3143*303); %moles iniciales de gas
b=16*pi*k*r0^2/(3*n0);
y0=49000;
eta=0.0289*9.8*y0/(8.3143*303);
n=45; %número de moles
a=n/n0;
M=1.12;  %masa del globo
c=M/(0.0289*n0);
f=@(x) x^3+(c-a)*x^2/b-1;
lambda=sqrt(fzero(f,1.5));
%altura de equilibrio
yMax=y0-((b+a*lambda^4-b*lambda^6)/lambda^7)^(1/(eta-1))*y0;
fprintf('Altura máxima %4.1f\n',yMax);

%velocidad con la que asciende el globo
h=zeros(1,100);
v=zeros(1,100);
i=1;
for y=0:yMax/100:yMax
    h(i)=y;
    fp=@(x) (1-y/y0)^(eta-1)*x^7+b*x^6-a*x^4-b;
    lambda=fzero(fp,1.5);
    v(i)=sqrt((20*9.8*r0/3)*(lambda-c*(1-y/y0)^(1-eta)/lambda^2));
    i=i+1;
end
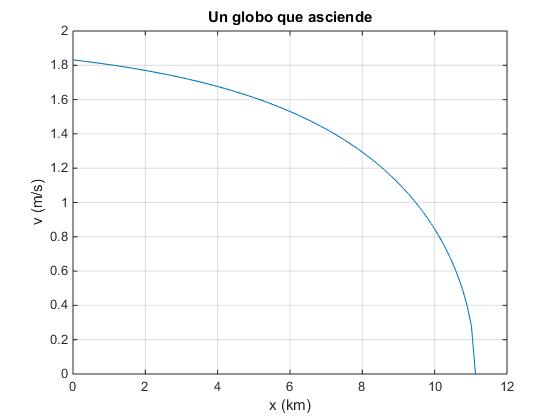
plot(h/1000,v)
grid on
xlabel('x (km)')
ylabel('v (m/s)')
title('Un globo que asciende')

Altura máxima 11128.5

Actividades

Se introduce

• La masa M del globo incluyendo el gas y el lastre, en el control titulado Masa
• El número n de moles de gas con el que se infla el globo, en el control titulado Moles.

Se pulsa el botón titulado Nuevo

Si el empuje es mayor que el peso el globo asciende. Sobre el globo también actúa una fuerza de rozamiento proporcional al cuadrado de la velocidad que mantiene en todo momento el globo en equilibrio, (la aceleración es nula). Sin embargo, la velocidad cambia debido a que el empuje cambia con la altura del globo.

Observamos:

En la parte izquierda, la variación de la presión con la altura,

${\displaystyle P=P_0{\left(1-\frac{y}{y_0}\right)}^{\eta }}$

se suministra el dato de la temperatura en grados centígrados.

${\displaystyle T=T_0\left(1-\frac{y}{y_0}\right)}$

Una franja de color rojo, nos indica que la densidad del aire disminuye con la altura, el color rojo oscuro indica aire más denso y el color rojo claro aire menos denso.

${\displaystyle \rho ={\rho }_0{\left(1-\frac{y}{y_0}\right)}^{\eta -1}}$

En la franja se mueve el globo y se muestran mediante flechas las fuerzas que actúan sobre el mismo:

• Peso, en color negro
• El empuje, en color rojo
• La fuerza de rozamiento, en color azul

En la parte superior derecha, se muestra el globo, como se incrementa su radio a medida que asciende.

En la parte inferior derecha, se representa la velocidad del globo en función de la altura.

Observamos que la velocidad se mantiene casi constante e igual a la velocidad inicial durante casi todo el trayecto de ascensión y disminuye rápidamente, en las proximidades de la altura máxima que alcanza.

Referencias

Theoretical Question 2. International Physics Olympiad Competition 2004 in South Korea.

Merritt D. R., Weinhaus F. The pressure curve for a rubber balloon. Am. J. Phys. 46 (10) October 1978. pp. 976-977