Campo eléctrico producido por todas las cargas del conductor

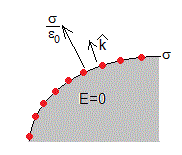
En las páginas anteriores hemos estudiado los conductores:

• El campo en el interior de un conductor es cero. El exceso de carga se sitúa en la superficie del conductor.
• La dirección del campo eléctrico en las proximidades de la superficie de un conductor es perpendicular a dicha superficie (la dirección del vector unitario $\widehat{k}$ ) y su módulo es σ/ε₀, siendo σ la carga por unidad de superficie

${\displaystyle \begin{array}{l}{\overrightarrow{E}}_{\text{interior}}=0\hfill \\ {\overrightarrow{E}}_{\text{exterior}}=\frac{\sigma }{{\epsilon }_0}\widehat{k}\hfill \end{array}}$

Campo eléctrico producido por las cargas contenidas en un elemento dA

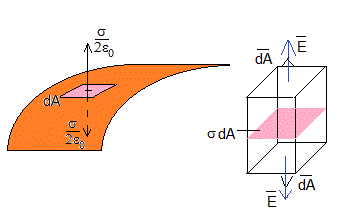
En la figura, se muestra una porción de la superficie de un conductor cargado con σ C/m², en dicha superficie tomamos un elemento de área dA alrededor de un punto P. Aplicando la ley de Gauss vamos a calcular el campo producido por la carga dq=σ·dA que contiene este elemento diferencial de área.

Consideremos la superficie cerrada en forma de paralepípedo de la figura de la derecha. La dirección del campo eléctrico es perpendicular a la superficie que contiene la carga dA. Por la superficie lateral del paralepípedo no hay flujo, ya que el vector campo eléctrico y el vector superficie son perpendiculares. El flujo del campo eléctrico a través de una de las bases es $\overrightarrow{E}·\overrightarrow{dA}=E·dA·\cos 0º=E·dA$ .

El flujo total del campo eléctrico producido por la carga dq=σ·dA a través de la superficie del paralepípedo es 2E·dA. Aplicando la ley de Gauss

${\displaystyle \begin{array}{l}{{\displaystyle \oint }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}=\frac{q}{{\epsilon }_0}\\ 2E·dA=\frac{\sigma ·dA}{{\epsilon }_0}E=\frac{\sigma }{2{\epsilon }_0}\end{array}}$

El elemento de carga dq=σ·dA produce la mitad del campo total en el punto P, en las proximidades de la superficie del conductor, en el interior y en el exterior, tal como se muestra en la figura

${\displaystyle \begin{array}{l}{\overrightarrow{E}}_{\text{interior}}=-\frac{\sigma }{2{\epsilon }_0}\widehat{k}\hfill \\ {\overrightarrow{E}}_{\text{exterior}}=\frac{\sigma }{2{\epsilon }_0}\widehat{k}\hfill \end{array}}$

Campo eléctrico producido por las restantes cargas del conductor

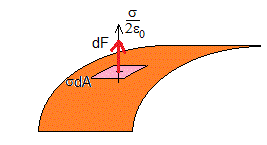
Vamos a calcular el campo producido por las restantes cargas del conductor, sabiendo el campo producido por todas las cargas del conductor

Si el elemento de carga dq=σ·dA produce la mitad del campo total en el exterior, el resto de las cargas del conductor producirán en la posición que ocupa dicho elemento dA la otra mitad σ/ε₀.

${\displaystyle \begin{array}{l}{\overrightarrow{E}}_{\text{interior}}=\frac{\sigma }{2{\epsilon }_0}\widehat{k}\hfill \\ {\overrightarrow{E}}_{\text{exterior}}=\frac{\sigma }{2{\epsilon }_0}\widehat{k}\hfill \end{array}}$

El campo eléctrico producido por las restantes cargas del conductor en el punto P de la superficie del conductor tiene un único valor σ/(2ε₀)

La fuerza dF que ejerce este campo sobre la carga dq contenida en el elemento de área dA vendrá dada por el producto

${\displaystyle dF=\frac{\sigma }{2{\epsilon }_0}\sigma ·dA}$

La fuerza por unidad de área, denominada presión electrostática es

${\displaystyle \frac{dF}{dA}=\frac{{\sigma }^2}{2{\epsilon }_0}}$

Campo producido por una esfera conductora

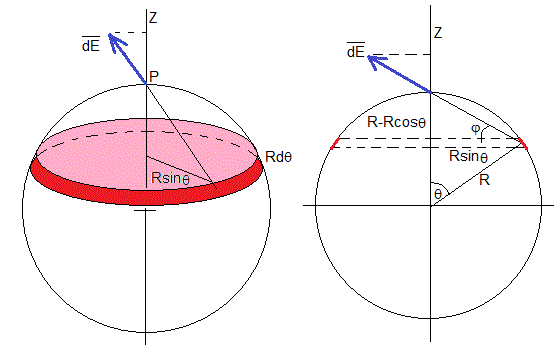
Consideremos una esfera conductora de radio R, con una carga q uniformemente distribuida en su superficie con densidad σ=q/(4πR²). Calculamos el campo producido por esta distribución de carga en el punto P

Por simetría el campo eléctrico tiene dirección radial y en el punto P, su dirección será a lo largo del eje Z de la esfera

Calculamos el campo eléctrico producido por la porción de carga dq contenida en la banda de radio Rsinθ y anchura R·dθ señalada en color rojo y a continuación, su proyección sobre el eje Z.

El área de esta banda es 2πRsinθ(R·dθ). El modulo del campo que produce en P es

${\displaystyle dE=\frac{1}{4\pi {\epsilon }_0}\frac{2\pi \sigma R^2\sin \theta ·d\theta }{{\left(R-R\cos \right)}^2+{\left(R\sin \theta \right)}^2}}$

Su proyección sobre el eje Z es, dE_z=dE·sinφ

Establecemos la relación entre los ángulo θ y φ

${\displaystyle \begin{array}{l}\tan \phi =\frac{R-R\cos \theta }{R\sin \theta }=\tan \frac{\theta }{2}\\ \phi =\frac{\theta }{2}\end{array}}$

La proyección del campo $\overrightarrow{dE}$ a lo largo del eje Z es

${\displaystyle d{E}_z=\frac{\sigma }{4{\epsilon }_0}\cos \frac{\theta }{2}d\theta }$

El campo producido por la carga de la esfera conductora en el punto P es la suma de todas las componentes Z

${\displaystyle E_P=\frac{\sigma }{4{\epsilon }_0}{\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \frac{\theta }{2}d\theta }=\frac{\sigma }{2{\epsilon }_0}{\displaystyle \underset{0}{\overset{\pi }{\int }}\left(\cos \frac{\theta }{2}\right)d}\frac{\theta }{2}=\frac{\sigma }{2{\epsilon }_0}}$

Que es el resultado que obtuvimos anteriormente, para un conductor de forma cualesquiera

Fuerza de atracción entre las placas de un condensador

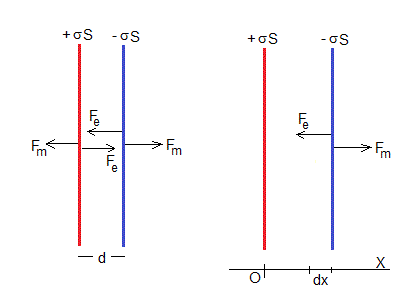
Consideremos un condensador plano-paralelo, formado por dos placas de área S y separadas d, cargadas con cargas iguales y opuestas σS. Las placas se atraen con una fuerza F_e, para mantenerlas separadas, tendremos que aplicar dos fuerzas iguales y opuestas F_m a cada una de las placas tal como se muestra en la figura.

La energía del condensador cargado es

${\displaystyle U=\frac{1}{2}\frac{q^2}{C}=\left(\frac{{\sigma }^2}{2{\epsilon }_0}\right)\left(Sd\right)}$

Supongamos que las placas están aisladas, de forma que la carga no cambia, mantenemos fija la placa izquierda en el origen y desplazamos la otra placa una distancia dx, realizando un trabajo F_m·dx. El campo eléctrico no cambia (es constante entre las placas del condensador), el volumen del condensador cambia S·dx y también la energía dU.

${\displaystyle \begin{array}{l}dU=\left(\frac{{\sigma }^2}{2{\epsilon }_0}\right)\left(Sdx\right)=F_{m}dx\\ F_m=\frac{{\sigma }^2}{2{\epsilon }_0}S\end{array}}$

De nuevo encontramos la expresión de la fuerza por unidad de área

Referencias

Paul Lorrain, Dale R. Corson. Campos y ondas electromagnéticos. Selecciones Científicas. 1972. págs. 83-86