Para una función no periódica P-->∞

${\displaystyle F(\omega )={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(t)e^{-i\omega t}dt}f(t)=\frac{1}{2\pi }{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}F(\omega )e^{i\omega t}d\omega }}$

La primera integral que obtiene F(ω) se denomina transformada de Fourier de f(t), y la segunda se denomina transformada inversa de Fourier.

El cuadrado f²(t) nos da una idea de cómo la energía contenida en la onda se distribuye en el tiempo, mientas que F²(ω) nos da una idea de como la energía se distribuye en el espectro de frecuencias. Naturalmente,

${\displaystyle {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\left|f(t)\right|}^{2}dt=}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\left|F(\omega )\right|}^{2}d\omega }}$

Pulso rectangular

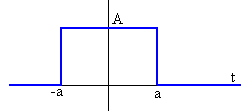
Sea un pulso rectangular tal que f(t) es cero excepto en el intervalo [-a,a] que vale A, tal como se muestra en la figura

La transformada de Fourier de f(t) vale

${\displaystyle \begin{array}{l}F(\omega )={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(t)\exp (-i\omega t)·dt}\\ F(\omega )={\displaystyle \underset{-a}{\overset{a}{\int }}A\exp (-i\omega t)·dt}=\frac{2A}{\omega }\sin (\omega a)\end{array}}$

>> syms a t w;
>> int('exp(-i*w*t)',t,-a,a)
ans =(2*sin(a*w))/w

Alternativamente, utilizamos la función fourier de MATLAB

syms a t;
ft=heaviside(t+a)-heaviside(t-a);
Fw=fourier(ft);
Fw=simplify(Fw)

ft=subs(ft,a,1);
subplot(2,1,1)
ezplot(ft,[-2,2]);
ylim([-0.2 1.2])
xlabel('t');
ylabel('f(t)')
title('Pulso rectangular')

Fw=subs(Fw,a,1);
subplot(2,1,2)
hg=ezplot(Fw,[-10,10]);
set(hg,'color','r')
ylim([-1 2.2])
xlabel('\omega');
ylabel('F(\omega)')
title('Transformada de Fourier')
grid on

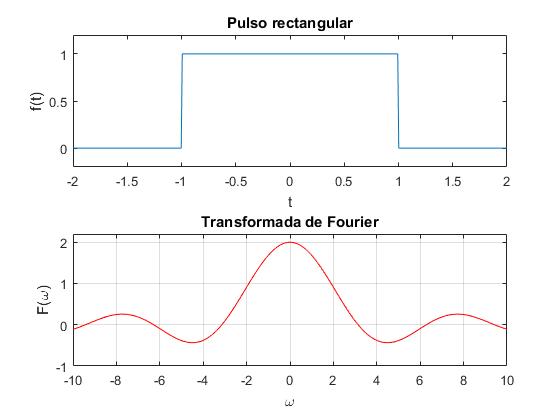
En la figura vemos un pulso rectangular de semianchura a=1 y su transformada de Fourier

No es necesario utilizar Math Symbolic Toolbox para dibujar la función y su transformada de Fourier como vemos en este script.

t=[-2 -1 -1 1 1 2];
ft=[0 0 1 1 0 0];
subplot(2,1,1)
plot(t,ft,'b');
ylim([-0.2 1.2])
xlabel('t');
ylabel('f(t)')
title('Pulso rectangular')

fw=@(w) 2*sin(w+eps)./w;
subplot(2,1,2)
fplot(fw,[-10,10], 'color','r');
ylim([-1,2.2])
xlabel('\omega');
ylabel('F(\omega)')
grid on

Pulso triangular

${\displaystyle f(t)=\{\begin{array}{l}1+\frac{t}{a}-a\le t<0\\ 1-\frac{t}{a}0\le t<a\\ 0\text{otros }t\end{array}}$

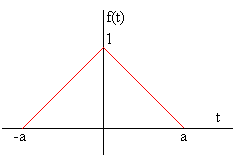
La transformada de Fourier es

${\displaystyle \begin{array}{l}F(\omega )={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(t)\exp (-i\omega t)dt=}\\ {\displaystyle \underset{-a}{\overset{0}{\int }}\left(1+\frac{t}{a}\right)\exp (-i\omega t)dt}+{\displaystyle \underset{0}{\overset{a}{\int }}\left(1-\frac{t}{a}\right)\exp (-i\omega t)dt=}\frac{4{\sin }^2\left(\omega a/2\right)}{a{\omega }^2}\end{array}}$

>> syms t a w;
>> f1=(1+t/a)*(heaviside(t+a)-heaviside(t))*exp(-i*w*t);
>> f2=(1-t/a)*(heaviside(t)-heaviside(t-a))*exp(-i*w*t);
>> Fw=int(f1,t,-a,0)+int(f2,t,0,a)
Fw =1/(a*w^2) - (1/exp(a*w*i))/(a*w^2) - (exp(a*w*i) - 1)/(a*w^2)
>> Fw=simplify(Fw)
Fw =(4*sin((a*w)/2)^2)/(a*w^2)

syms t;
ft=(1-t)*(heaviside(t)-heaviside(t-1))+(1+t)*(heaviside(t+1)-heaviside(t));
Fw=fourier(ft);
Fw=simplify(Fw)

subplot(2,1,1)
ezplot(ft,[-2,2]);
ylim([-0.2 1.2])
xlabel('t');
ylabel('f(t)')
title('Pulso triangular')

subplot(2,1,2)
hg=ezplot(Fw,[-10,10]);
set(hg,'color','r')
ylim([-0.1 1.1])
xlabel('\omega');
ylabel('F(\omega)')
title('Transformada de Fourier')
grid on

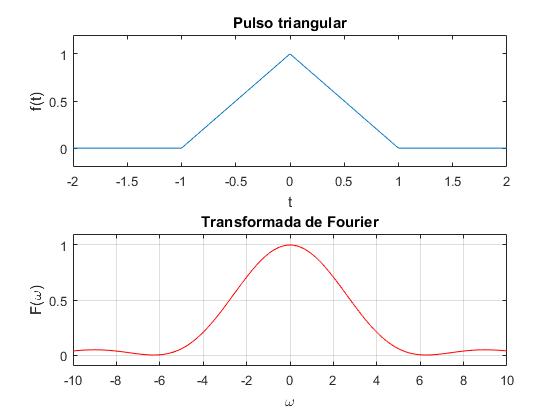
En la ventana de comandos aparece la transformada de Fourier, que es la misma que hemos deducido con a=1

>> Fw=-(2*cos(w) - 2)/w^2

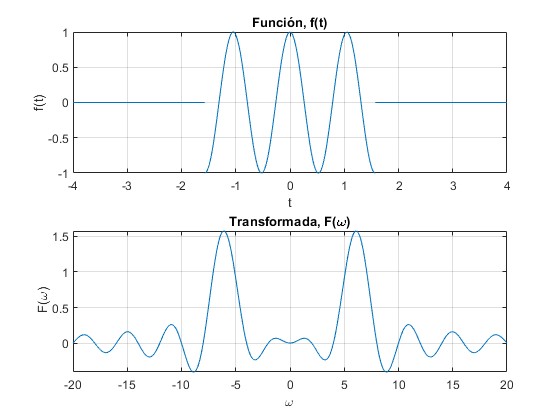
Función coseno limitado

Sea la función f(t) definida en el intervalo [-b/2, b/2]

${\displaystyle f(t)=\{\begin{array}{l}A\cos \left({\omega }_{0}t\right),-\frac{b}{2}\le t\le \frac{b}{2}\\ 0\end{array}}$

Su transformada de Fourier es

${\displaystyle \begin{array}{l}F\left(\omega \right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(t)\exp \left(-i\omega t\right)dt=A{\displaystyle \underset{-b/2}{\overset{b/2}{\int }}\cos \left({\omega }_{0}t\right)\exp \left(-i\omega t\right)dt}}\\ A\left\{{\displaystyle \underset{-b/2}{\overset{b/2}{\int }}\cos \left({\omega }_{0}t\right)\cos \left(\omega t\right)dt+i{\displaystyle \underset{-b/2}{\overset{b/2}{\int }}\cos \left({\omega }_{0}t\right)\sin \left(\omega t\right)dt}}\right\}\end{array}}$

La segunda integral es nula, el intervalo de integración es simétrico y la función es impar

>> syms w w0 b t;
>> int(cos(w0*t)*sin(w*t), t,-b/2, b/2)
ans =0

El resultado de la primera integral es

${\displaystyle \begin{array}{l}A{\displaystyle \underset{-b/2}{\overset{b/2}{\int }}\cos \left({\omega }_{0}t\right)\cos \left(\omega t\right)dt=}\frac{A}{2}{\displaystyle \underset{-b/2}{\overset{b/2}{\int }}\left(\cos \left(\left({\omega }_0-\omega \right)t\right)+\cos \left(\left({\omega }_0+\omega \right)t\right)\right)dt=}\\ \frac{A}{2}{\left\{\frac{\sin \left(\left({\omega }_0-\omega \right)t\right)}{{\omega }_0-\omega }+\frac{\sin \left(\left({\omega }_0+\omega \right)t\right)}{{\omega }_0+\omega }\right\}|}_{-b/2}^{b/2}\\ F\left(\omega \right)=A\frac{\sin \left(\left({\omega }_0-\omega \right)\frac{b}{2}\right)}{{\omega }_0-\omega }+\frac{\sin \left(\left({\omega }_0+\omega \right)\frac{b}{2}\right)}{{\omega }_0+\omega }\end{array}}$

b=pi;
w0=6;
subplot(2,1,1)
fplot(@(t) cos(w0*t),[-b/2,b/2])
line([-4,-b/2],[0,0])
line([b/2,4],[0,0])
grid on
xlabel('t')
ylabel('f(t)')
title('Función, f(t)')
subplot(2,1,2)
f=@(w) sin((w0+w)*b/2)./(w0+w)+sin((w0-w)*b/2)./(w0-w);
fplot(f,[-20,20])
grid on
xlabel('\omega')
ylabel(' F(\omega)')
title('Transformada, F(\omega)')

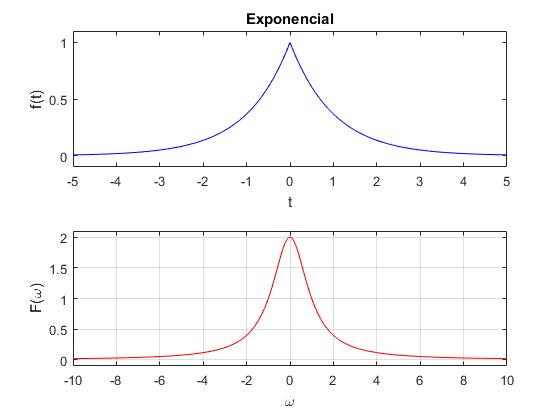
Función exponencial

Transformada de Fourier de la función f(t)=Aexp(-γ|t|)

Primero, calculamos la transformada de Fourier de la función f(t)=Aexp(-γt)·u(t). La integración de f(t) se extiende entre 0 e ∞

${\displaystyle \begin{array}{l}F(\omega )={\displaystyle \underset{0}{\overset{\infty }{\int }}A{e}^{-\gamma t}{e}^{-i\omega t}dt=}{\displaystyle \underset{0}{\overset{\infty }{\int }}A\exp \left(-(\gamma +i\omega )t\right)dt=}{-\frac{A}{\gamma +i\omega }\exp \left(-(\gamma +i\omega )t\right)|}_0^{\infty }=\\ \frac{A}{\gamma +i\omega }\gamma >0\end{array}}$

A continuación, tenemos en cuenta la propiedad de la transformada de Fourier de la función f(-t) es F(-ω), la transformada de las dos exponenciales es la suma

${\displaystyle F(\omega )=\frac{A}{\gamma +i\omega }+\frac{A}{\gamma -i\omega }=A\frac{2\gamma }{{\gamma }^2+{\omega }^2}}$

g=1;
ft=@(t) exp(-g*abs(t));
subplot(2,1,1)
fplot(ft,[-5,5],'color','b');
ylim([-0.1 1.1])
xlabel('t');
ylabel('f(t)')
title('Exponencial')

Fw=@(w) 2*g./(g^2+w.^2);
subplot(2,1,2)
fplot(Fw,[-10,10],'color','r');
ylim([-0.1 2.1])
xlabel('\omega');
ylabel('F(\omega)')
grid on

Oscilación amortiguada

En este ejemplo calculamos la trasnformada de Fourier de la función que describe una oscilación amortiguada que parte del instante t=0.

${\displaystyle f(t)=\exp (-\gamma t)\cos ({\omega }_{0}t)}$

Escribimos f(t) en forma equivalente y calculamos su transformada de Fourier

$$\begin{gathered} {\displaystyle \begin{array}{l}f(t)=\frac{1}{2}\exp (-\gamma t)\left(\exp (i{\omega }_{0}t)+\exp (-i{\omega }_{0}t)\right)\\ F(\omega )={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(t)\exp (-i\omega t)dt=} \\ \frac{1}{2}\left({\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\gamma t-i(\omega -{\omega }_0)t\right)dt+{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\gamma t-i(\omega +{\omega }_0)t\right)dt}}\right)=\\ \frac{1}{2}{\left(\frac{\exp \left(-\gamma t-i(\omega -{\omega }_0)t\right)}{-\gamma -i(\omega -{\omega }_0)}+\frac{\exp \left(-\gamma t-i(\omega +{\omega }_0)t\right)}{-\gamma -i(\omega +{\omega }_0)}\right)}_0^{\infty }=\\ \frac{1}{2}\left(\frac{1}{\gamma +i(\omega -{\omega }_0)}+\frac{1}{\gamma +i(\omega +{\omega }_0)}\right)=\frac{1}{2}\left(\frac{\gamma -i(\omega -{\omega }_0)}{{\gamma }^2+{(\omega -{\omega }_0)}^2}+\frac{\gamma -i(\omega +{\omega }_0)}{{\gamma }^2+{(\omega +{\omega }_0)}^2}\right)\end{array}} \end{gathered}$$

g=1; %amortiguamiento
w0=6; %frecuencia angular
ft=@(t) exp(-g*t).*cos(w0*t);
subplot(2,1,1)
fplot(ft,[0,5],'color','b');
ylim([-1 1.1])
xlabel('t');
ylabel('f(t)')
title('Oscilación amortiguada')

Fw=@(w) abs(((g-1i*(w-w0))./(g^2+(w-w0).^2)+(g-1i*(w+w0))./(g^2+(w+w0).^2))/2);
subplot(2,1,2)
fplot(Fw,[-10,10],'color','r');
ylim([-0.1 0.6])
xlabel('\omega');
ylabel('F(\omega)')
title('Transformada')
grid on

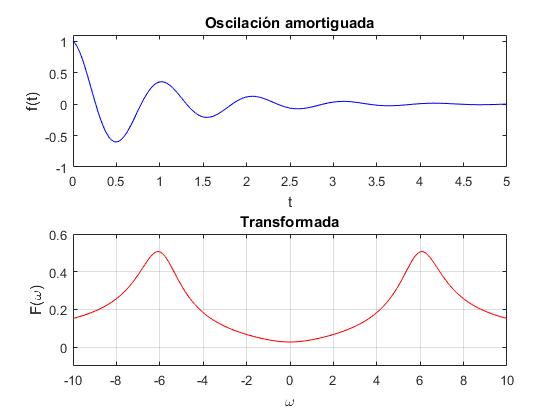
Como F(ω) es complejo, representamos el módulo

Función de Gauss

La función de Gauss es una de las funciones más importantes, se define

${\displaystyle f(x)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left(-\frac{{(x-\mu )}^2}{2{\sigma }^2}\right)}$

donde μ es la media y σ es la desviación estándar de acuerdo con su interpretación estadística.

x=-5:0.05:5;
s2=[0.2,1,5,0.5]; %cuadrado de la desviación estándar
mu=[0,0,0,-2]; %media 
col=['b','g','r','k'];
hold on
for k=1:length(s2)
    y=exp(-(x-mu(k)).^2/(2*s2(k)))/sqrt(s2(k)*2*pi);
    str=sprintf('\\mu=%1.1f, \\sigma^2=%1.1f',mu(k),s2(k));
    plot(x,y,col(k),'displayName',str)
end
hold off
xlabel('x')
ylabel('f(x)')
legend('-DynamicLegend','location','NorthEast')
title('Función de Gauss')
grid on

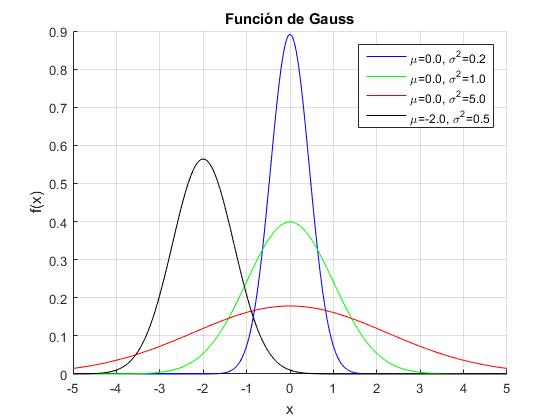
El máximo de la función se produce para x=μ. Denominamos Δx a la anchura de la función de Gauss para una ordenada igual a la mitad del máximo. Por ejemplo, en la curva de color verde el máximo vale y=0.4, aproximadamente. Determinamos el intervalo de valores de x, Δx cuya ordenada y≥0.2.

${\displaystyle \begin{array}{l}\frac{1}{2}\frac{1}{\sigma \sqrt{2\pi }}=\frac{1}{\sigma \sqrt{2\pi }}\exp \left(-\frac{x_1^2}{2{\sigma }^2}\right)\\ x_1=\sigma \sqrt{2\ln 2}\\ \Delta x=2\sigma \sqrt{2\ln 2}\end{array}}$

Sea f(t) una función de Gauss

${\displaystyle f(t)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left(-\frac{t^2}{2{\sigma }^2}\right){\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(t)·dt}=1}$

>> syms t;
>> syms s2 positive;
>> f=exp(-t^2/(2*s2))/(sqrt(2*pi*s2));
>> int(f,t,-inf,inf)
ans =1

Para calcular la transformada de Fourier tenemos que partir del resultado de la integral

${\displaystyle I={\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-\alpha x^2)dx}=\frac{1}{2}\sqrt{\frac{\pi }{\alpha }}}$

que se justifica del siguiente modo:

${\displaystyle \begin{array}{l}I={\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-\alpha x^2)dx}I={\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-\alpha y^2)dx}\\ I^2={\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\alpha (x^2+y^2)\right)dx·dy}}\\ x^2+y^2=r^{2}dx·dy=r·dr·d\theta \\ I^2={\displaystyle \underset{0}{\overset{\pi /2}{\int }}{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\alpha r^2\right)r·dr·d\theta =}}\frac{\pi }{2}{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\alpha r^2\right)r·dr=\frac{\pi }{4\alpha }}\\ I={\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-\alpha x^2)dx}=\frac{1}{2}\sqrt{\frac{\pi }{\alpha }}\end{array}}$

Con ayuda de este resultado calculamos la transformada de Fourier de un pulso descrito por una función de Gauss

${\displaystyle \begin{array}{l}F(\omega )={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(t)·\exp (-i\omega t)·dt}=\frac{1}{\sigma \sqrt{2\pi }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-\frac{t^2}{2{\sigma }^2}\right)}\exp (-i\omega t)·dt=\\ \frac{1}{\sigma \sqrt{2\pi }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-\frac{t^2}{2{\sigma }^2}-i\omega t\right)}·dt\\ F(\omega )=\frac{1}{\sigma \sqrt{2\pi }}\exp \left(-\frac{{\sigma }^2{\omega }^2}{2}\right){\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-\frac{{(t+i{\sigma }^2\omega )}^2}{2{\sigma }^2}\right)}·dt\\ F(\omega )=\exp \left(-\frac{{\sigma }^2{\omega }^2}{2}\right)\end{array}}$

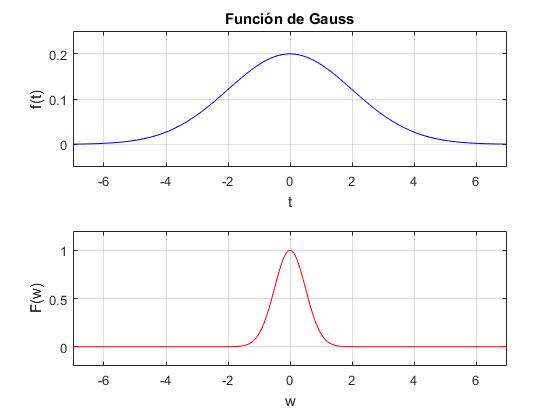
La tansformada de Fourier de una función de Gauss es otra función de Gauss

>> syms t;
>> syms s positive;
>> ft=exp(-t^2/(2*s^2))/(s*sym('sqrt(2*pi)'));
>> Fw=fourier(ft)
Fw =1/exp((s^2*w^2)/2)

Se sugiere comprobar que cuanto es mayor σ, más ancha es la curva f(t) y más estrecha es la curva F(ω) y viceversa.

sigma=2;
ft=@(t) exp(-t.^2/(2*sigma^2))/(sigma*sqrt(2*pi));
subplot(2,1,1)
fplot(ft,[-7,7],'color','b');
ylim([-0.05 0.25])
xlabel('t');
ylabel('f(t)')
title('Función de Gauss')
grid on

fw=@(w) exp(-w.^2*sigma^2/2);
subplot(2,1,2)
fplot(fw,[-7,7],'color','r');
ylim([-0.2,1.2])
xlabel('w');
ylabel('F(w)')
grid on

Función delta de Dirac δ(t)

La función delta de Dirac tiene la siguiente definición

${\displaystyle \begin{array}{l}\delta (t)=\{\begin{array}{l}0t\ne 0\\ \infty t=0\end{array}\\ {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\delta (t)·dt=1}\\ {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(t)\delta (t-a)·dt=f(a)}\end{array}}$

Se obtiene a partir de una función de Gauss cuyo parámetro σ tiende a cero

${\displaystyle \begin{array}{l}f(t)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left(-\frac{t^2}{2{\sigma }^2}\right)\\ \lim \underset{\sigma \to 0}{f(t,\sigma )}=\delta (t)\end{array}}$

Calculamos la transformada inversa de Fourier de la función delta de Dirac.

${\displaystyle \begin{array}{l}F(\omega )=2\pi ·\delta \left(\omega -{\omega }_0\right)\\ f(t)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\delta \left(\omega -{\omega }_0\right)\exp (-i\omega t)dt}=\exp (-i{\omega }_{0}t){\displaystyle \underset{{\omega }_0^{+}}{\overset{{\omega }_0^{-}}{\int }}\delta \left(\omega -{\omega }_0\right)dt}=\exp (-i{\omega }_{0}t)\end{array}}$

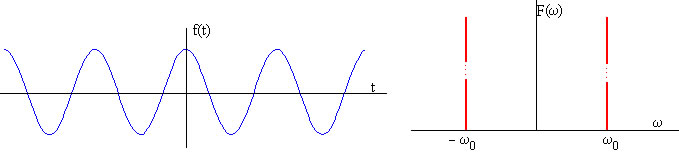
F(ω) es cero para todos los valores de ω, excepto para ω=ω₀. El área bajo la curva δ(ω-ω₀) es la unidad.

>> syms w w0;
>> Fw=2*pi*dirac(w-w0);
>> ft=ifourier(Fw)
ft =exp(w0*x*i)

Teniendo en cuenta que

${\displaystyle \cos \left({\omega }_{0}t\right)=\frac{1}{2}\left(\exp (i{\omega }_{0}t)+\exp (-i{\omega }_{0}t)\right)}$

la transformada de Fourier F(ω)=π[δ(ω-ω₀)+δ(ω+ω₀)]

>> syms w w0;
>> Fw=pi*(dirac(w-w0)+dirac(w+w0));
>> ft=ifourier(Fw)
ft =(1/exp(w0*x*i))/2 + exp(w0*x*i)/2
>> simplify(ft) 
ans =cos(w0*x)

De otro modo

${\displaystyle \begin{array}{l}f(x)=\cos (k_{0}x)=\frac{1}{2}\left(\exp (i{k}_{0}x)+\exp (i{k}_{0}x)\right)\\ F(k)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(x)\exp (-ikx)dx=}\\ \frac{1}{2}\left({\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-i(k-k_0)x\right)dx+{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-i(k+k_0)x\right)dx}}\right)=\\ \pi \left(\delta (k-k_0)+\delta (k+k_0)\right)\end{array}}$

Dos funciones delta de Dirac situadas en +k₀ y en -k₀.

>> syms k0 x;
>> fx=cos(k0*x);
>> Fk=fourier(fx)
Fk =pi*(dirac(k0 - w) + dirac(k0 + w))

Combinación de las funciones coseno y Gauss

En primer lugar, vamos a obtener el resultado de la integral

${\displaystyle \begin{array}{l}I={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-\frac{u^2}{2{\sigma }^2}+iuy\right)}du={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-{\left(\frac{u}{\sqrt{2}\sigma }-i\frac{y\sigma }{\sqrt{2}}\right)}^2-\frac{y^2{\sigma }^2}{2}\right)}du=\\ \exp \left(-\frac{y^2{\sigma }^2}{2}\right){\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-{\left(\frac{u}{\sqrt{2}\sigma }-i\frac{y\sigma }{\sqrt{2}}\right)}^2\right)}du\end{array}}$

Haciendo el cambio de variable

${\displaystyle x=\frac{u}{\sqrt{2}\sigma }-i\frac{y\sigma }{\sqrt{2}}dx=\frac{1}{\sqrt{2}\sigma }du}$

Obtenemos

${\displaystyle I=\sqrt{2}\sigma \exp \left(-\frac{y^2{\sigma }^2}{2}\right){\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-x^2\right)}dx}$

Sabiendo el resultado de la integral

${\displaystyle {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-x^2\right)}dx=\sqrt{\pi }}$

Obtenemos el resultado

${\displaystyle I=\sqrt{2\pi }\sigma \exp \left(-\frac{y^2{\sigma }^2}{2}\right)}$

que utlizaremos más adelante.

Transformada de Fourier

Vamos a obtener la transformada de Fourier de la función

${\displaystyle \begin{array}{l}f(x)=\exp \left(-\frac{{\left(x-x_0\right)}^2}{2{\sigma }_x^2}\right)\cos \left(k_{0}x\right)\\ =\frac{1}{2}\exp \left(-\frac{{\left(x-x_0\right)}^2}{2{\sigma }_x^2}\right)\left(\exp (i{k}_{0}x)+\exp (-i{k}_{0}x)\right)\end{array}}$

En primer lugar, obtenemos la transformada de Fourier F₁(k) de la función f₁(x)

${\displaystyle \begin{array}{l}{f}_1(x)=\exp \left(i{k}_{0}x-\frac{{\left(x-x_0\right)}^2}{2{\sigma }_x^2}\right)\\ F_1(k)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(x)\exp (-ikx)dx}={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-ikx+i{k}_{0}x\right)}\exp \left(-\frac{{\left(x-x_0\right)}^2}{2{\sigma }_x^2}\right)dx\\ F_1(k)=\exp \left(-i(k-k_0)x_0\right){\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(i(k_0-k)(x-x_0)-\frac{{\left(x-x_0\right)}^2}{2{\sigma }_x^2}\right)}dx\end{array}}$

Tenemos una integral del tipo descrito al principio de este apartado

${\displaystyle \begin{array}{l}u=x-x_{0}du=dx\\ y=k_0-k\sigma ={\sigma }_x\\ F_1(k)=\exp \left(-i(k-k_0)x_0\right){\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(iyu-\frac{u^2}{2{\sigma }^2}\right)}du\\ F_1(k)=\sqrt{2\pi }{\sigma }_x\exp \left(i{k}_0{x}_0\right)\exp \left(-ik{x}_0\right)\exp \left(-\frac{{\left(k_0-k\right)}^2{\sigma }_x^2}{2}\right)\end{array}}$

De modo análogo, obtenemos la transformada de Fourier de la función f₂(x)

${\displaystyle \begin{array}{l}{f}_2(x)=\exp \left(-i{k}_{0}x-\frac{{\left(x-x_0\right)}^2}{2{\sigma }_x^2}\right)\\ F_2(k)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(x)\exp (-ikx)dx}={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-ikx-i{k}_{0}x\right)}\exp \left(-\frac{{\left(x-x_0\right)}^2}{2{\sigma }_x^2}\right)dx\\ F_2(k)=\exp \left(-i(k+k_0)x_0\right){\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(i(-k_0-k)(x-x_0)-\frac{{\left(x-x_0\right)}^2}{2{\sigma }_x^2}\right)}dx\\ u=x-x_{0}du=dx\\ y=-(k_0+k)\sigma ={\sigma }_x\\ F_2(k)=\sqrt{2\pi }{\sigma }_x\exp \left(-i{k}_0{x}_0\right)\exp \left(-ik{x}_0\right)\exp \left(-\frac{{\left(k_0+k\right)}^2{\sigma }_x^2}{2}\right)\end{array}}$

La transformada de Fourier de la función f(x)= f₁(x)+ f₂(x) es F(k)=(F₁(k)+F₂(k))/2

x0=0;
k0=2;
s2=5;
x=-10:0.05:10;
fx=exp(-(x-x0).^2/(2*s2)).*cos(k0*x);
subplot(2,1,1)
plot(x,fx,'b')
grid on
xlabel('x')
ylabel('f(x)')
title('Función')

k=-5:0.05:5;
Fk=sqrt(2*pi*s2)*exp(-1i*k*x0).*(exp(1i*k0*x0)*exp(-(k-k0).^2*s2/2)...
+exp(-1i*k0*x0)*exp(-(k+k0).^2*s2/2))/2;
subplot(2,1,2)
plot(k,abs(Fk),'r')
grid on
xlabel('k')
ylabel('F(k)')
title('Transformada')

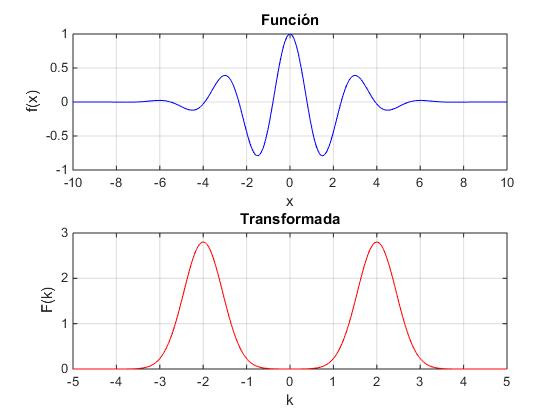
En la parte superior de la figura, vemos la función coseno, cuya envolvente (amplitud) es la función de Gauss.

No hay cambio apreciable en el valor absoluto de F(k) cuando se modifica la posición del centro de la función de Gauss, x₀ a un valor distinto de cero. La transformada de Fourier de esta función consiste en dos picos centrados en ±k₀.

Si incrementamos el parámetro σ² a una valor grande por ejemplo, 100, vemos que la amplitud de la función f(x) es casi constante, y su transformada de Fourier son dos picos puntiagudos centrados en ±k₀ que se van aproximando a una función delta de Dirac a medida que se incrementa σ²

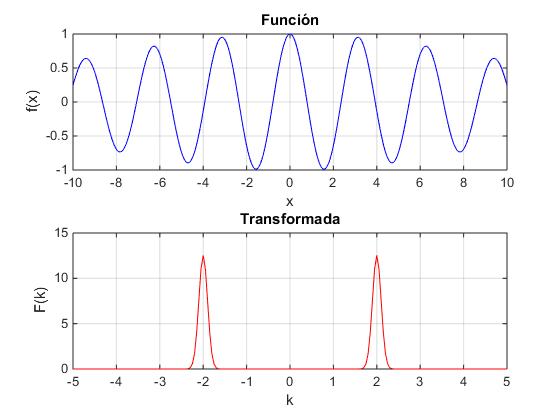
Tabla de transformadas de Fourier

>> ft=sym('1');
>> Fw=fourier(ft)
Fw =2*pi*dirac(w)

>> syms t;
>> ft=heaviside(t);
>> Fw=fourier(ft)
Fw =pi*dirac(w) - i/w
 
>> ft=dirac(t);
>> Fw=fourier(ft)
Fw =1

>> syms a positive;
>> ft=exp(-a*t)*heaviside(t);
>> Fw=fourier(ft)
Fw =1/(a + w*i)

>> ft=t*exp(-a*t)*heaviside(t);
>> Fw=fourier(ft)
Fw =1/(a + w*i)^2

Transformada de Fourier de una función periódica f(t) de semiperiodo P.

${\displaystyle f(t)={\displaystyle \sum _{-\infty }^{\infty }{c}_k\exp \left(ik\pi \frac{t}{P}\right)}F(\omega )=2\pi {\displaystyle \sum _{-\infty }^{\infty }{c}_k\delta \left(\omega -k{\omega }_0\right)}{\omega }_0=\frac{\pi }{P}}$

Transformada de f(t-T)

${\displaystyle \begin{array}{l}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(t-T)\exp \left(-i\omega t\right)dt}={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(\xi )\exp \left(-i\omega (\xi +T)\right)d\xi }=\\ \exp \left(-i\omega T\right){\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(\xi )\exp \left(-i\omega \xi \right)d\xi =}\exp \left(-i\omega T\right)F(\omega )\end{array}}$

Transformada de exp(iω₀t)f(t)

${\displaystyle {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(t)\exp \left(i{\omega }_{0}t\right)\exp \left(-i\omega t\right)dt}={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(t)\exp \left(-i(\omega -{\omega }_0)t\right)dt}=F(\omega -{\omega }_0)}$

Transformada de f(at) para a>0

${\displaystyle {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(at)\exp \left(-i\omega t\right)dt}=\frac{1}{a}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(\xi )\exp \left(-i\omega \xi /a\right)d\xi }=\frac{1}{a}F\left(\frac{\omega }{a}\right)}$