Modos normales de vibración de una barra elástica

Extremos fijos

Para encontrar los modos normales de vibración de una barra elástica con ambos extremos fijos seguimos un procedimiento similar

La ecuación diferencial del movimiento de un elemento de la barra es

$\frac{\partial^{4} ψ}{\partial x^{4}} + \frac{ρ a b}{Y I} \frac{\partial^{2} ψ}{\partial t^{2}} = 0$

Siendo ψ el desplazamiento trasversal de un punto x de la barra en el instante t.

ρ es la densidad de la barra

Y es el módulo de Young del material de la barra.

I=ab³/12 es el momento de inercia de la sección trasversal rectangular de la barra de anchura a y espesor b.

Estudiamos una solución de la forma

ψ(x,t)=y(x)·sin(ωt)

Cada punto x de la barra vibra con una amplitud y(x) y con frecuencia angular ω.

La ecuación diferencial se convierte en

$\frac{d^{4} y}{d x^{4}} - \frac{ρ a b}{Y I} ω^{2} y = 0$

Las raíces de la ecuación característica son

$r^{4} - q^{4} = 0 q = {(\frac{ρ a b}{Y I} ω^{2})}^{1 / 4}$

son dos raíces reales y dos imaginarias

r=q, r=-q, r=iq, r=-iq

La solución general es

$y (x) = C_{1} e^{q x} + C_{2} e^{- q x} + C_{3} e^{i q x} + C_{4} e^{- i q x}$

o de forma equivalente

y=A₁sinh(qx)+A₂·cosh(qx)+A₃·sin(qx)+A₄·cos(qx)

La pendiente o derivada de y es,

$\frac{d y}{d x} = q (A_{1} \cosh (q x) + A_{2} \sinh (q x) + A_{3} \cos (q x) - A_{4} \sin (q x))$

Condiciones de contorno.

La barra está firmemente sujeta por sus extremo x=0 y la pendiente en este punto es dy/dx=0.

0=A₂+A₄0=A₁+A₃

La barra está firmemente sujeta por sus extremo x=L, y la pendiente en este punto es dy/dx=0.

0=A₁(sinh(qL)-sin(qL))+A₂(cosh(qL)-cos(qL))
0=A₁(cosh(qL)-cos (qL))+A₂(sinh(qL)+sin(qL))

Eliminado A₁ y A₂ obtenemos una ecuación transcendente en qL

cosh(qL)·cos (qL)=1

Las raíces r_n=q_n·L de esta ecuación se calculan por algún procedimiento numérico, sus primeros cinco valores son:

r_n=4.73, 7.85, 11.00, 14.14, 17.27

Conocido los valores posibles de q_n se calculan las frecuencias de vibración ω_n=2πf_n

$f_{n} = \frac{r_{n}^{2}}{2 π} \sqrt{\frac{Y I}{ρ a b L^{4}}} = C_{n} \sqrt{\frac{Y I}{ρ a b L^{4}}}$

Donde f_n es la frecuencia del modo normal n de vibración y C_n es un número que corresponde a este modo. Sus primeros valores son:

C₁=3.56, C₂=9.82, C₃=19.2, C₄=31.8, C₅=47.5, etc.

El coeficiente C_n es independiente de las características de la barra y el segundo término, bajo la raíz, depende del material y de las dimensiones de la barra.

La amplitud de la vibración y(x) de los distintos puntos x de la barra en el modo normal de vibración n es:

$y_{n} (x) = A {(sinh (q_{n} x) - sin (q_{n} x)) - \frac{sinh (q_{n} L) - sin (q_{n} L)}{cosh (q_{n} L) - cos (q_{n} L)} (cosh (q_{n} x) - cos (q_{n} x))}$

El valor de la constante de proporcionalidad A es la escala vertical. Para que todos los modos de vibración estén dibujados a la misma escala, se calcula A por procedimientos numéricos, de modo que

$\int_{0}^{L} y_{n}^{2} (x) d x = cte$

%barra elástica de longitud 1
x=linspace(1,15,30);
f=@(x) cosh(x).*cos(x)-1;
r=raices(f,x);
hold on
for q=r
    g=@(x) (sinh(q*x)-sin(q*x))-(sinh(q)-sin(q))*
(cosh(q*x)-cos(q*x))/(cosh(q)-cos(q));
    h=@(x) g(x).^2;
    A=sqrt(integral(h,0,1));   %integral sustituye a quad
    x=linspace(0,1,100);
    plot(x, -g(x)/A, 'displayName',num2str(q^2/(2*pi)))
 end
 hold off
 grid on
 legend('-DynamicLegend','location','southwest')
 xlabel('x')
 ylabel('y')
 title('Modos de vibración de una barra')

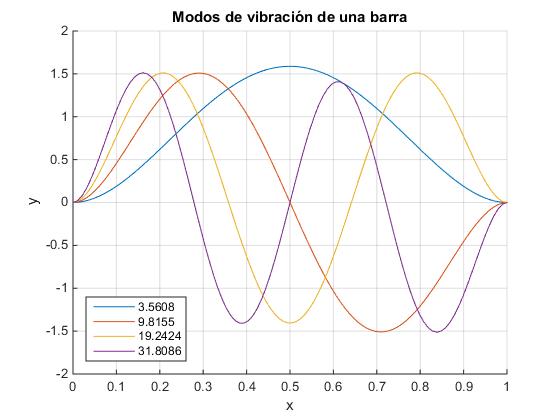
>> r =    4.7300    7.8532   10.9956   14.1372

Aproximaciones

Cuando qL es grande exp(-qL)≈0 y el seno y el coseno hiperbólico se pueden aproximar a exp(-qL)/2.

Con esta aproximación la ecuación transcendente

(sinh(qL)-sin(qL))·(sinh(qL)+sin(qL))-(cosh(qL)-cos (qL))²=0

se reduce a

cos(qL)=1/exp(qL).

Si qL es grande cos(qL)=0, Las raíces de esta ecuación son

q_nL=π/2+nπ

Los cinco primeros valores de r_n=q_nL son

r_n=4.71, 7.85, 11.00, 14.14, 17.28.

Son prácticamente los mismos, que los calculados resolviendo la ecuación transcendente por procedimientos numéricos

La amplitud y(x) de los distintos puntos x de la barra en el modo normal de vibración n se puede aproximar a

$\begin{array}{l} y_{n} (x) \approx A {(sinh (q_{n} x) - sin (q_{n} x)) - (cosh (q_{n} x) - cos (q_{n} x))} \\ = A (- \exp (- q_{n} x) + cos (q_{n} x) - sin (q_{n} x)) \end{array}$

Se puede calcular el valor aproximado de la integral

$\begin{array}{l} \int_{0}^{L} y_{n}^{2} (x) d x = \int_{0}^{L} {1 - sin (2 q_{n} x) + \exp (- 2 q_{n} x) + 2 \exp (- q_{n} x) (sin (q_{n} x) -cos (q_{n} x))} d x = \\ {x + \frac{\cos (2 q_{n} x)}{2 q_{n}} - \frac{\exp (- 2 q_{n} x)}{2 q_{n}} - 2 \frac{\exp (- q_{n} x)}{q_{n}} sin (q_{n} x)}_{0}^{L} \approx L \end{array}$

Para obtener el integrando, hay que integrar dos veces por partes exp(-q_nx)·sin(q_nx), y lo mismo, exp(-q_nx)·cos (q_nx).

Para calcular el valor aproximado de la integral, se ha despreciado los términos exp(-q_nL) y exp(-2q_nL) y por otra parte, cos(2q_nL)=0.

Ejemplo:

Sea una barra de acero densidad ρ=7.8 g/cm³, módulo de Young Y=20.6·10¹⁰ N/m²

de dimensiones a=2.54 cm de ancho, b=0.76 mm de espesor y longitud L=20.3 cm.

El momento de inercia de la sección trasversal es

I=ab³/12=9.29·10^-13 m⁴

La frecuencia del modo fundamental de vibración vale

$f_{1} = 3.56 \sqrt{\frac{20.6 \cdot 10^{10} \cdot 9.29 \cdot 10^{- 13}}{7800 \cdot 0.0254 \cdot 0.00076 \cdot {0.203}^{4}}} = 3.56 \cdot 27.36 = 97 Hz$

La frecuencia del segundo modo normal de vibración será

f₂=9.82·27.36=269 Hz

y así, sucesivamente.

Se puede diseñar una experiencia que permita excitar un modo normal de vibración de la barra, medir la frecuencia con un osciloscopio, y calcular el módulo de Young de la barra. Previamente, se miden las dimensiones de la barra (longitud, anchura y espesor) con los instrumentos adecuados y se pesa en una balanza para determinar su densidad (masa/volumen).

Un extremo libre

Para encontrar los modos normales de vibración de una barra elástica con un extremo libre seguimos un procedimiento similar

La solución general de la ecuación que describe las vibraciones de una barra es.

ψ(x,t)=y(x)·sin(ωt)

La solución de la ecuación diferencial, la amplitud y(x) de la vibración de los puntos x de la barra

y(x)=A₁sinh(qx)+A₂·cosh(qx)+A₃·sin(qx)+A₄·cos(qx)

Las condiciones de contorno cambian

La barra está firmemente sujeta por su extremo izquierdo x=0, y la pendiente en este punto es dy/dx=0.

$\frac{d y}{d x} = q (A_{1} \cosh (q x) + A_{2} sinh (q x) + A_{3} \cos (q x) - A_{4} sin (q x))$

0=A₂+A₄0=A₁+A₃

En el extremo derecho libre x=L, y(L) y su pendiente dy/dt no son cero, pero el momento y la fuerza son cero, lo que implica que d²y/dx²=0 y d³y/dx³=0

$\begin{array}{l} \frac{d^{2} y}{d x^{2}} = q^{2} (A_{1} \sinh (q x) + A_{2} \cosh (q x) - A_{3} \sin (q x) - A_{4} \cos (q x)) \\ \frac{d^{3} y}{d x^{3}} = q^{3} (A_{1} \cosh (q x) + A_{2} \sinh (q x) - A_{3} \cos (q x) + A_{4} \sin (q x)) \end{array}$

A₁(sinh(qL)+sin(qL))+A₂(cosh(qL)+cos(qL))=0
A₁(cosh(qL)+cos (qL))+A₂(sinh(qL)-sin(qL))=0

Eliminado A₁ yA₂ obtenemos una ecuación transcendente en qL

cosh(qL)·cos (qL)=-1

Las raíces r_n=q_n·L de esta ecuación se calculan por procedimientos numéricos, sus primeros valores son:

r_n=1.875, 4.693, 7.855, 10.996, …

Conocido los valores posibles de q_n se calculan las frecuencias de vibración ω_n=2πf_n

$f_{n} = \frac{r_{n}^{2}}{2 π} \sqrt{\frac{Y I}{ρ a b L^{4}}} = C_{n} \sqrt{\frac{Y I}{ρ a b L^{4}}}$

Donde f_n es la frecuencia del modo normal n de vibración y C_n es un número que corresponde a este modo. Sus primeros valores son:

C₁=0.56,C₂=3.51,C₃=9.82,C₄=19.24, …

El coeficiente C_n es independiente de las características de la barra y el segundo término, bajo la raíz, depende del material y de las dimensiones de la barra.

La amplitud y(x) de los distintos puntos x de la barra en el modo normal de vibración n es:

$y_{n} (x) = A {(sinh (q_{n} x) - sin (q_{n} x)) - \frac{sinh (q_{n} L) + sin (q_{n} L)}{cosh (q_{n} L) + cos (q_{n} L)} (cosh (q_{n} x) - cos (q_{n} x))}$

$\int_{0}^{L} y_{n}^{2} (x) d x = cte$

%barra elástica de longitud 1
f=@(x) cosh(x).*cos(x)+1;
x=linspace(1,10,30);
r=raices(f,x);
hold on
 for q=r
    g=@(x) (sinh(q*x)-sin(q*x))-(sinh(q)+sin(q))*(cosh(q*x)-cos(q*x))
/(cosh(q)+cos(q));
    h=@(x) g(x).^2;
    A=sqrt(integral(h,0,1));  
    x=linspace(0,1,100);
    plot(x, -g(x)/A, 'displayName',num2str(q^2/(2*pi)))
 end
 hold off
 grid on
 legend('-DynamicLegend','location','southwest')
 xlabel('x')
 ylabel('y')
 title('Modos de vibración de una barra')

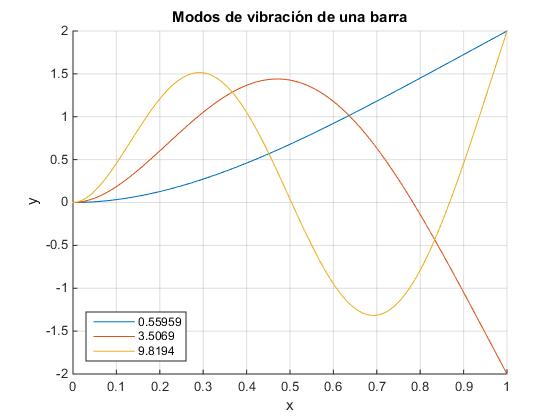
r =    1.8751    4.6941    7.8548

Ejemplo:

Sea una barra de acero del ejemplo del apartado anterior

Densidad ρ=7.8 g/cm³, módulo de Young Y=20.6·10¹⁰ N/m²

de dimensiones a=2.54 cm de ancho, b=0.76 mm de espesor y longitud L=20.3 cm.

El momento de inercia de la sección trasversal es

I=ab³/12=9.29·10^-13 m⁴

La frecuencia del modo fundamental de vibración es, f₁=0.56·27.36=15.3 Hz
La frecuencia del segundo modo normal de vibración es, f₂=3.51·27.36=96.0 Hz

y así, sucesivamente.

Los dos extremos libres

Para encontrar los modos normales de vibración de una barra elástica con los dos extremos libres seguimos un procedimiento similar

La solución general de la ecuación que describe las vibraciones de una barra es.

ψ(x,t)=y(x)·sin(ωt)

La solución de la ecuación diferencial, la amplitud y(x) de la vibración de los puntos x de la barra

$\begin{array}{l} y = A_{1} \sinh (q x) + A_{2} \cosh (q x) + A_{3} \sin (q x) + A_{4} \cos (q x) \\ \frac{d y}{d x} = q (A_{1} \cosh (q x) + A_{2} \sinh (q x) + A_{3} \cos (q x) - A_{4} \sin (q x)) \end{array}$

Las condiciones de contorno

El extremo izquierdo libre x=0, la ordenda y y la pendiente dy/dt no son cero, pero el momento y la fuerza son cero, lo que implica que d²y/dx²=0 y d³y/dx³=0

0=A₂-A₄0=A₁-A₃

En el extremo derecho libre x=L, y(L) y su pendiente dy/dt no son cero, pero el momento y la fuerza son cero, lo que implica que d²y/dx²=0 y d³y/dx³=0

A₁(sinh(qL)-sin(qL))+A₂(cosh(qL)-cos(qL))=0
A₁(cosh(qL)-cos (qL))+A₂(sinh(qL)+sin(qL))=0

Eliminado A₁ yA₂ obtenemos una ecuación transcendente en qL

cosh(qL)·cos (qL)=1

Ecuación que ya hemos obtenido para el caso de extremos fijos. Las raíces r_n=q_n·L de esta ecuación se calculan por procedimientos numéricos, sus primeros valores son:

r_n=4.7300, 7.8532, 10.99564, ....

Conocido los valores posibles de q_n se calculan las frecuencias de vibración ω_n=2πf_n

$f_{n} = \frac{r_{n}^{2}}{2 π} \sqrt{\frac{Y I}{ρ a b L^{4}}} = C_{n} \sqrt{\frac{Y I}{ρ a b L^{4}}}$

Donde f_n es la frecuencia del modo normal n de vibración y C_n es un número que corresponde a este modo. Sus primeros valores son:

C₁=3.56,C₂=9.82,C₃=19.24, …

El coeficiente C_n es independiente de las características de la barra y el segundo término, bajo la raíz, depende del material y de las dimensiones de la barra.

La amplitud y(x) de los distintos puntos x de la barra en el modo normal de vibración n es:

$y_{n} (x) = A {\cosh (q x) + \cos (q x) + \frac{\cosh (q_{n} L) - \cos (q_{n} L)}{\sin (q_{n} L) - \sinh (q_{n} L)} (\sinh (q x) + \sin (q x))}$

$\int_{0}^{L} y_{n}^{2} (x) d x = cte$

%barra elástica de longitud 1
f=@(x) cosh(x).*cos(x)-1;
x=linspace(1,11,30);
r=raices(f,x);
hold on
 for q=r
    g=@(x) (cosh(q*x)+cos(q*x))+(sinh(q*x)+sin(q*x))*
(cosh(q)-cos(q))/(sin(q)-sinh(q));
    h=@(x) g(x).^2;
    A=sqrt(integral(h,0,1));  
    x=linspace(0,1,100);
    plot(x, -g(x)/A, 'displayName',num2str(q^2/(2*pi)))
 end
 hold off
 grid on
 legend('-DynamicLegend','location','northwest')
 xlabel('x')
 ylabel('y')
 title('Modos de vibración de una barra')

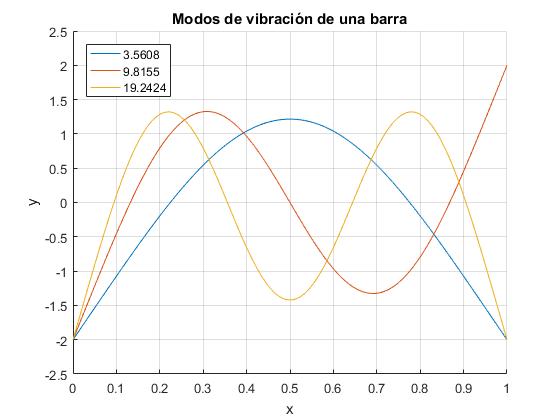
r =    4.7300    7.8532   10.9956

Ejemplo:

Sea una barra de acero del ejemplo del apartado anterior

Densidad ρ=7.8 g/cm³, módulo de Young Y=20.6·10¹⁰ N/m²

de dimensiones a=2.54 cm de ancho, b=0.76 mm de espesor y longitud L=20.3 cm.

El momento de inercia de la sección trasversal es

I=ab³/12=9.29·10^-13 m⁴

La frecuencia del modo fundamental de vibración es, f₁=3.56·27.36=97.4 Hz
La frecuencia del segundo modo normal de vibración es, f₂=3.51·27.36=268.5 Hz

y así, sucesivamente.

Referencias

Wilson F., Lord A. E.,Young's modulus determination via simple, inexpensive static and dynamic measurements. Am. J. Phys. 41, May 1973, pp. 653-656.

Turvey K. An undergraduate experiment on the vibration of a cantilever and its application to the determination of Young's modulus. Am. J. Phys. 58 (5) May 1990, pp. 483-487

G. William Baxter, Keith M. Hagenbuch. A Student Project on Wind Chimes. The Physics Teacher, Vol. 36, April 1998, pp. 204-208