Ecuaciones de Lagrange

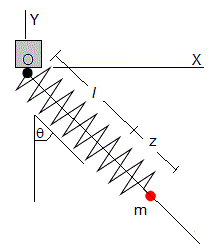
Consideremos un péndulo formado por una partícula de masa m que puede deslizar a lo largo de una varilla de masa despreciable, que oscila en el plano vertical. La partícula está unida al centro de oscilación O mediante un muelle de constante k.

La figura muestra el estado del sistema en un instante t. El muelle se ha deformado z, de modo que su longitud es l+z y la varilla forma un ángulo θ con la vertical.

Situamos el origen y los ejes en el centro de oscilación O, la posición de la partícula es

${\displaystyle \{\begin{array}{l}x=\left(l+z\right)\sin \theta \\ y=-\left(l+z\right)\cos \theta \end{array}}$

Derivando respecto del tiempo, obtenemos las componentes de su velocidad

${\displaystyle \{\begin{array}{l}\frac{dx}{dt}=\frac{dz}{dt}\sin \theta +\left(l+z\right)\cos \theta \frac{d\theta }{dt}\\ \frac{dy}{dt}=-\frac{dz}{dt}\cos \theta +\left(l+z\right)\sin \theta \frac{d\theta }{dt}\end{array}}$

Su energía cinética es

${\displaystyle T=\frac{1}{2}m\left({\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2\right)=\frac{1}{2}m\left({\left(\frac{dz}{dt}\right)}^2+{\left(l+z\right)}^2{\left(\frac{d\theta }{dt}\right)}^2\right)}$

Su energía potencial se compone de dos términos: la energía potencial gravitatoria y la energía potencial elástica del muelle deformado z

${\displaystyle V=mgy+\frac{1}{2}k{z}^2=-mg\left(l+z\right)\cos \theta +\frac{1}{2}k{z}^2}$

La lagrangiana es

${\displaystyle \begin{array}{l}L=T-V=\frac{1}{2}m\left({\left(\frac{dz}{dt}\right)}^2+{\left(l+z\right)}^2{\left(\frac{d\theta }{dt}\right)}^2\right)+mg\left(l+z\right)\cos \theta -\frac{1}{2}k{z}^2\\ L=\frac{1}{2}m\left({\dot{z}}^2+{\left(l+z\right)}^2{\dot{\theta }}^2\right)+mg\left(l+z\right)\cos \theta -\frac{1}{2}k{z}^2\end{array}}$

Las ecuaciones del movimiento de Lagrange nos llevan al sistema de dos ecuaciones diferenciales. La primera es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \left(l+z\right)\frac{d^2\theta }{d{t}^2}+2\frac{d\theta }{dt}\frac{dz}{dt}+g\sin \theta =0\end{array}}$

La segunda ecuación diferencial es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{z}}\right)-\frac{\partial L}{\partial z}=0\\ \frac{d^{2}z}{d{t}^2}+\frac{k}{m}z-(l+z){\left(\frac{d\theta }{dt}\right)}^2-g\cos \theta =0\end{array}}$

Resolveremos este sistema de dos ecuaciones diferenciales con las siguientes condiciones iniciales

${\displaystyle t=0\{\begin{array}{l}\theta ={\theta }_0\frac{d\theta }{dt}=0\\ z=z_0\frac{dz}{dt}=0\end{array}}$

donde z₀ es la deformación inicial del muelle y θ₀ el ángulo inicial que forma la varilla con la vertical.

Casos particulares

En el caso de un muelle muy rígido. La segunda ecuación diferencial se escribe

${\displaystyle \begin{array}{l}z=\frac{m}{k}\left(g\cos \theta +(l+z){\left(\frac{d\theta }{dt}\right)}^2-\frac{d^{2}z}{d{t}^2}\right)\\ k\to \infty z\to 0\end{array}}$

La primera ecuación diferencial se reduce a la del movimiento de un péndulo simple de longitud l. La frecuencia de las oscilaciones de pequeña amplitud sinθ≈θ es ${\omega }_1^2=g/l$

${\displaystyle l\frac{d^2\theta }{d{t}^2}+g\sin \theta =0}$

Cuando la varilla no se desvía de la posición de equilibrio, θ=0. La segunda ecuación diferencial se transfroma en

${\displaystyle \frac{d^{2}z}{d{t}^2}+\frac{k}{m}z-g=0}$

que es la ecuación del movimiento oscilatorio de una partícula unida a un muelle elástico. La frecuencia de la oscilación es ${\omega }_2^2=k/m$

Posiciones de equilibrio

Igualando a cero las derivadas de z y θ respecto del tiempo t

${\displaystyle \begin{array}{l}{\theta }_1=0z_1=\frac{mg}{k}\\ {\theta }_2=\pi z_2=-\frac{mg}{k}\end{array}}$

La primera, corresponde a un equilibrio estable y la segunda a un equilibrio inestable.

Solución numérica de las ecuaciones del movimiento

Para resolver este sistema de ecuaciones diferenciales. Despejamos d²θ/dt² en la primera ecuación y d²z/dt² en la segunda

${\displaystyle \begin{array}{l}\frac{d^2\theta }{d{t}^2}=-\frac{1}{l+z}\left(2\frac{d\theta }{dt}\frac{dz}{dt}+g\sin \theta \right)\\ \frac{d^{2}z}{d{t}^2}=(l+z){\left(\frac{d\theta }{dt}\right)}^2+g\cos \theta -\frac{k}{m}z\end{array}}$

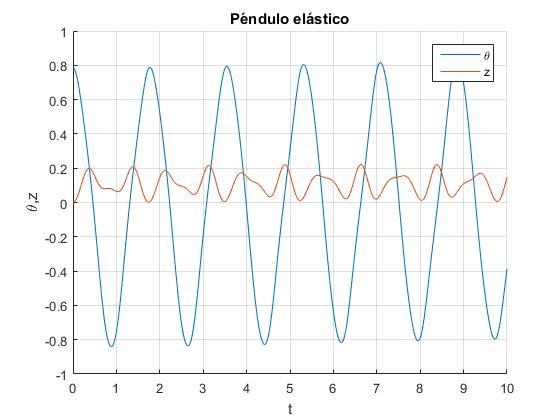
Elaboramos un script con los siguientes valores de los parámetros que podremos modificar: el cociente k/m=100, donde k es la constante del muelle y m la masa de la partícula, longitud del muelle sin deformar l=0.5. A continuación, las condiciones iniciales: Desplazamiento angular inicial del péndulo θ₀=π/4, deformación inicial del muelle z₀=0. Velocidadades iniciales a lo largo de la partícula en la dirección tangencial dθ/dt=0 y en la radial dz/dt=0.

Se resuelve el sistema de ecuaciones diferenciales mediante el procedimiento ode45, durante un tiempo de 10 s. Se representa la deformación del muelle z y la posición angular del péndulo θ en función del tiempo t.

k=100; %constante del muelle/masa partícula
L=0.5; %longitud del muelle sin deformar
%condiciones iniciales
x0=[pi/4,0,0,0]; %condiciones iniciales
tspan=[0,10];
% x(1)=theta, x(2)=dtheta/dt, x(3)=z; x(4)=dz/dt
fg=@(t,x)[x(2);-(9.8*sin(x(1))+2*x(2)*x(4))/(L+x(3)); x(4); 
(L+x(3))*x(2)^2+9.8*cos(x(1))-k*x(3)];
[t,x]=ode45(fg,tspan,x0);
hold on
plot(t,x(:,1)) 
plot(t,x(:,3))
%plot(t,x(:,2)) 
%plot(t,x(:,4))
hold off
grid on
legend('\theta','z');
xlabel('t')
ylabel('\theta,z')
title('Péndulo elástico')

Comprobamos que la energía total E=T+V permanece constante

${\displaystyle E=T+V=\frac{1}{2}m\left({\left(\frac{dz}{dt}\right)}^2+{\left(l+z\right)}^2{\left(\frac{d\theta }{dt}\right)}^2\right)-mg\left(l+z\right)\cos \theta +\frac{1}{2}k{z}^2}$

>> E=(x(:,4).^2+((L+x(:,3)).^2).*x(:,2).^2)/2
-9.8*(L+x(:,3)).*cos(x(:,1))+k*x(:,3).^2/2
E =
   -3.4648
   -3.4648
   -3.4648
   -3.4648
   -3.4648
   -3.4648
   ...

Actividades

En primer lugar, especificamos los parámetros del sistema

• El cociente k/m, la constante elástica k entre la masa m de la partícula, el control titulado Constante/masa
• La longitud del muelle sin deformar se ha fijado en l=0.5

En segundo lugar, especificamos las condiciones iniciales

• La desviación inicial θ₀ del péndulo en grados, en el control titulado Angulo péndulo
• La deformación inicial del muelle z₀, en el control titulado Deformación muelle
• La velocidades iniciales de la partícula a lo largo de la dirección tangencial dθ/dt=0 y radial dz/dt=0

Si queremos ver las gráficas de la deformación z del muelle (en color azul) y la posición angular θ del péndulo (en color rojo), activamos la casilla titulada Gráfica

Se resuelve el sistema de dos ecuaciones diferenciales por el procedimiento de Runge-Kutta. El programa calcula la energía del sistema E en cada instante y lo compara con la energía inicial E₀. Si la desviación es mayor que el 1% el programa se detiene.

${\displaystyle \left|\frac{E-E_0}{E_0}\right|<0.01}$

Segunda ley de Newton

Colocamos muelle elástico de constante k y longitud L₀ sin deformar en posición vertical, lo fijamos por el extremo superior y colocamos una partícula de masa m en su extremo libre inferior.

El muelle elástico se estira una longitud y_e=mg/k, la longitud del muelle es L_e=L₀+y_e.

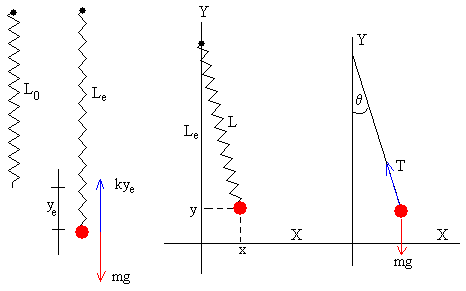
Situamos el origen del sistema de coordenadas en la posición de la partícula en equilibrio. Desplazamos la partícula a la posición (x₀, y₀) y la soltamos. Cuando la partícula está en la posición (x, y), la longitud del muelle deformado es L, las fuerzas sobre la partícula son:

• La fuerza T que ejerce el muelle deformado
• El peso mg de la partícula

Aplicamos la segunda ley de Newton

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-T\sin \theta \\ m\frac{d^{2}y}{d{t}^2}=T\text{cos}\theta -mg\end{array}}$

Sustituyendo T=k(L-L₀), mg=k(L_e-L₀), y teniendo en cuenta que sinθ=x/L, y cosθ=(L_e-y)/L, el sistema de ecuaciones diferenciales se escribe en función de la posición (x, y) de la partícula.

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=-\frac{k}{m}(L-L_0)\frac{x}{L}\\ \frac{d^{2}y}{d{t}^2}=\frac{k}{m}(L-L_0)\frac{(L_e-y)}{L}-\frac{k}{m}(L_e-L_0)\end{array}}$

La longitud del muelle deformado es

${\displaystyle L=\sqrt{{(L_e-y)}^2+x^2}}$

Es importante hacer notar, que la no linealidad de las ecuaciones diferenciales procede de la geometría no del muelle cuyo comportamiento se supone lineal.

Se resuelve el sistema de ecuaciones diferenciales por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, la posición inicial es x₀, y₀, y parte del reposo.

Aproximaciones

Cuando los desplazamientos x e y de la posición de equilibrio son pequeños en comparación con la longitud del muelle L₀, el sistema de ecuaciones diferenciales se puede expresar de forma más simple.

En la primera ecuación diferencial, el término

${\displaystyle \begin{array}{l}(L-L_0)\frac{x}{L}=x-\frac{L_0}{L}x\\ \frac{L_0}{L}=\frac{1}{\sqrt{\frac{x^2}{L_0^2}+\frac{y^2}{L_0^2}-\frac{2L_{e}y}{L_0^2}+\frac{L_e^2}{L_0^2}}}\approx \frac{1}{\sqrt{-\frac{2L_{e}y}{L_0^2}+\frac{L_e^2}{L_0^2}}}=\frac{L_0}{L_e}{\left(1-\frac{2y}{L_e}\right)}^{-1/2}\approx \frac{L_0}{L_e}+\frac{L_0}{L_e^2}y\end{array}}$

La primera ecuación diferencial, se escribe

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=-\frac{k}{m}\left(1-\frac{L_0}{L_e}\right)x+\frac{k}{m}\frac{L_0}{L_e^2}xy\\ \frac{d^{2}x}{d{t}^2}+\frac{g}{L_e}x=\frac{k}{m}\frac{L_0}{L_e^2}xy\end{array}}$

En la segunda ecuación diferencial, el término

${\displaystyle \begin{array}{l}(L-L_0)\frac{(L_e-y)}{L}-(L_e-L_0)=-y-\frac{L_0}{L}(L_e-y)+L_0=-y-L_0\frac{(L_e-y)}{\sqrt{{(L_e-y)}^2+x^2}}+L_0=\\ -y-L_0{\left(1+\frac{x^2}{{(L_e-y)}^2}\right)}^{-1/2}+L_0\approx -y-L_0\left(1-\frac{1}{2}\frac{x^2}{L_e^2}\right)+L_0=-y+\frac{1}{2}\frac{L_0}{L_e^2}{x}^2\end{array}}$

La segunda ecuación diferencial, se escribe

${\displaystyle \frac{d^{2}y}{d{t}^2}+\frac{k}{m}y=\frac{1}{2}\frac{k}{m}\frac{L_0}{L_e^2}{x}^2}$

Definimos ω_x la frecuencia de oscilación a largo del eje X, ω_y la frecuencia de oscilación a lo largo del eje Y, y λ la constante de proporcionalidad del acoplamiento como

${\displaystyle {\omega }_x^2=\frac{g}{L_e}{\omega }_y^2=\frac{k}{m}\lambda =\frac{k}{m}\frac{L_0}{L_e^2}}$

El sistema de dos ecuaciones diferenciales de segundo orden acopladas queda

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}+{\omega }_x^{2}x=\lambda xy\\ \frac{d^{2}y}{d{t}^2}+{\omega }_y^{2}y=\frac{\lambda }{2}{x}^2\end{array}}$

• La frecuencia ω_x corresponde a las oscilaciones de un péndulo de longitud L_e.

• La frecuencia ω_y corresponde a las oscilaciones de una masa m unida a un muelle elástico de constante k.

Supongamos que comenzamos a hacer oscilar la partícula muy próxima al eje Y, con x<<y. La solución de la segunda ecuación diferencial (se desprecia el término λx²) es, aproximadamente

y=Acos(ω_y·t)

La primera ecuación diferencial se convierte en

${\displaystyle \frac{d^{2}x}{d{t}^2}+\left({\omega }_x^2-\lambda A\cos ({\omega }_{y}t)\right)x=0}$

Esta ecuación diferencial se denomina del tipo Mathieu. Cuando

${\displaystyle \frac{{\omega }_y}{{\omega }_x}=\frac{2}{n}n=\text{1}\text{, 2}\text{, }\mathrm{..}}$

la solución es inestable incluso para pequeños valores del parámetro A (amplitud de la oscilación a lo largo del eje Y). Cuando menor sea n, más pronunciada es la inestabilidad. Así, para n=1, la relación entre las frecuencias angulares es

ω_y=2ω_x.

Los valores de la constante elástica k, de la longitud L₀ del muelle sin deformar, y de la masa m de la partícula que hacen que se cumpla esta relación son

${\displaystyle \begin{array}{l}{\omega }_y^2=4{\omega }_x^2\\ \frac{k}{m}=4\frac{g}{L_e}{L}_e=L_0+\frac{mg}{k}\\ L_0=\frac{3mg}{k}\end{array}}$

Energía del sistema

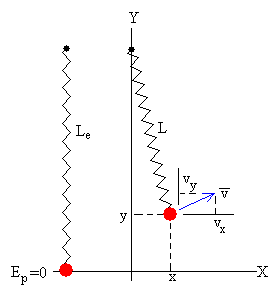
En la situación inicial, t=0,  la partícula unida al muelle elástica se libera (v=0) en la posición (x₀, y₀). Situamos el nivel cero de energía potencial E_p=0, en la posición de la partícula cuando se encuentra en equilibrio, tal como se muestra en la figura.

La energía inicial es

${\displaystyle E=mg{y}_0+\frac{1}{2}k{\left(\sqrt{x_0+{(L_e-y_0)}^2}-L_0\right)}^2}$

En el instante t la partícula se encuentra en la posición (x, y) y lleva una velocidad $\overrightarrow{v}=v_x\widehat{i}+v_y\widehat{j}$

La energía del sistema es

${\displaystyle E=\frac{1}{2}m(v_x^2+v_y^2)+mgy+\frac{1}{2}k{\left(\sqrt{x^2+{(L_e-y)}^2}-L_0\right)}^2}$

Actividades

Se introduce

• La constante elástica k del muelle en N/m, en el control titulado Constante k

• La masa m de la partícula, en g, en el control titulado Masa

• La longitud del muelle sin deformar se ha fijado en L₀=1 m

• Las coordenadas x₀ e y₀ de la posición inicial de la partícula en los controles titulados Posición x y Posición y

Se pulsa el botón titulado Nuevo

Se observa el movimiento de la partícula y su trayectoria

Ejemplo:

• La masa de la partícula m=300g=0.3 kg
• La longitud del muelle L₀=1.0 m

El valor de la constante k del muelle que hace que ω_y=2ω_x es k=8.82 N/m

En la posición de equilibrio el muelle se deforma y_e=mg/k=1/3 m. La longitud del muelle en la posición de equilibrio es L_e=1+1/3=4/3 m

Si partimos de una posición inicial muy próxima al eje vertical Y, por ejemplo, x₀=0.01 m e y₀=0.0, observamos como crecen las oscilaciones hacia uno y otro lado del eje vertical, del tipo péndulo, y disminuyen las oscilaciones tipo muelle. Luego, sucede el proceso inverso.

En la parte superior, se muestra la energía total de la partícula y la posición de la partícula (x, y) de la partícula en cada instante t.

En la parte derecha, se representan los tres tipos de energías mediante un diagrama de barras:

• energía cinética (color rojo)
• energía potencial gravitatoria (en color azul)
• energía potencial elástica (en color verde)

La suma de las tres clases de energía se mantiene constante.

Referencias

Del segundo apartado

Rusbridge M.G., Motion of the sprung pendulum. Am. J. Phys. 48 (2) February 1980, pp. 146-151.

Olsson M. G. Why does a mass on a spring sometimes misbehave?. Am. J. Phys. 44 (12) December 1976, pp. 1211-1212.