Un polinomio de grado n de coeficientes a₁,a₂...,a_n,a_n+1 es la expresión

a₁xⁿ+a₂x^n-1+...+a_nx+a_n+1

en MATLAB se representa por el vector fila p=[a₁,a₂...,a_n,a_n+1]

El polinomio p=x³-2x²+x-2 se representa por el vector p=[1 -2 1 -2]

Los polinomios se pueden representar de forma simbólica mediante la función poly2sym.

>> p=[1 -2 1 -2];
>> poly2sym(p)
ans =x^3 - 2*x^2 + x - 2

A su vez un polinomio en forma simbólica se puede convertir en el vector formado por sus coeficientes mediante sym2poly

>> syms x;
>> sym2poly(x^3-2*x-4)
ans =     1     0    -2    -4

Valor de un polinomio

Calculamos el valor de polinomio cuando se conoce el valor la variable x.

Sea p= x⁵- 3.5x⁴ + 2.75x³ + 2.125x² - 3.875x + 1.25

Cuando se expresa un polinomio de forma simbólica se utiliza la función subs

>> syms x;
>> p=x^5-3.5*x^4+2.75*x^3+2.125*x^2-3.875*x+1.25;
>> subs(p,x,1.5)
ans =   -0.6250

La función polyval nos proporciona este valor cuando se expresa el polinomio en forma de vector formado por los coeficientes.

>> p=[1 -3.5 2.75 2.125 -3.875 1.25];
>> x=1.5;
>> polyval(p,x)
ans =   -0.6250
>> x=0:0.5:2; 
>> polyval(p,x)
ans =    1.2500   0   -0.2500   -0.6250    0

La función ployval se puede utilizar para representar gráficamente un polinomio

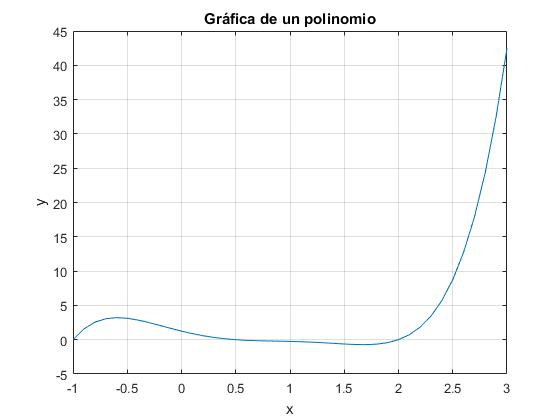
>> x=-1:0.1:3;
>> y=polyval([1 -3.5 2.75 2.125 -3.875 1.25],x);
>> plot(x,y)
>> grid on
>> xlabel('x')
>> ylabel('y')
>> title('Gráfica de un polinomio')

Suma de polinomios

Queremos sumar los polinomios p₁=x³-2x-4 y p₂=x²+3x+4

De forma simbólica

>> syms x;
>> p1=x^3-2*x-4;
>> p2=x^2+3*x+4;
>> p1+p2
ans =x^3 + x^2 + x

Para sumar dos polinomios en forma de vectores, los vectores tiene que tener las mismas dimensiones

>> p1=[1 0 -2 -4];
>> p2=[2 3 4];
>> p1+p2
??? Error using ==> plus
Matrix dimensions must agree.
>> p2=[0 2 3 4];
>> p1+p2
ans =     1     2     1     0

Producto de dos polinomios

Queremos multiplicar los polinomios p₁=x³-2x-4 y p₂=x²+3x+4

De forma simbólica

>> syms x;
>> p1=x^3-2*x-4;
>> p2=x^2+3*x+4;
>> p=p1*p2
p =-(x^2 + 3*x + 4)*(- x^3 + 2*x + 4)
>> expand(p)
ans =x^5 + 3*x^4 + 2*x^3 - 10*x^2 - 20*x - 16

Producto de dos polinomios mediante la función conv

>> p1=[1 0 -2 -4];
>> p2=[1 3 4];
>> p=conv(p1,p2)
p =     1     3     2   -10   -20   -16

Cociente

${\displaystyle \frac{x^3+5x^2+11x+13}{x^2+2x+4}=(x+3)+\frac{x+1}{x^2+2x+4}}$

De forma simbólica

>> syms x;
>> p1=x^3+5*x^2+11*x+13;
>> p2=x^2+2*x+4;
>> p=p1/p2
p =(x^3 + 5*x^2 + 11*x + 13)/(x^2 + 2*x + 4)
>> simplify(p)
ans =x + (x + 1)/(x^2 + 2*x + 4) + 3

La función deconv nos proporciona el cociente y el resto de la división entre dos polinomios.

>> p1=[1 5 11 13];
>> p2=[1 2 4];
>> [q r]=deconv(p1,p2)
q =     1     3
r =     0     0     1     1

Derivada

La regla de derivación de cada término de un polinomio es

${\displaystyle \frac{d}{dx}a{x}^n=n{a}^{n-1}}$

Mediante la función diff(p,n) calculamos la derivada n del polinomio p de forma simbólica

>> syms x;
>> p=x^3+4*x^2-3*x-2;
>> diff(p)
ans =3*x^2 + 8*x - 3
>> diff(p,2)
ans =6*x + 8

La función polyder calcula la derivada de un polinomio expresado en forma de vector formado por los coeficientes.

>> p=[1 4 -3 -2];
>> polyder(p)
ans =     3     8    -3

También calcula la derivada del producto de dos polinomios o del cociente de dos polinomios

${\displaystyle \begin{array}{l}\frac{d}{dx}(u·v)=u\frac{dv}{dx}+\frac{du}{dx}v\\ \frac{d}{dx}(x+1)(x-3)=2x-2\\ \frac{d}{dx}\left(\frac{u}{v}\right)=\frac{\frac{du}{dx}v-u\frac{dv}{dx}}{v^2}\\ \frac{d}{dx}\left(\frac{x+1}{x-3}\right)=\frac{-4}{{(x-3)}^2}=\frac{-4}{x^2-6x+9}\end{array}}$

>> p1=[1 1];
>> p2=[1 -3];
>> polyder(p1,p2)
ans =     2    -2
>> [q d]=polyder(p1,p2)
q =    -4
d =     1    -6     9

Integral

La integral de cada uno de los términos del polinomio se calcula mediante la fórmula

${\displaystyle {\displaystyle \int a{x}^{n}dx=}a\frac{x^{n+1}}{n+1}}$

La función int calcula la integral de forma analítica, suponiendo que la constante de integración vale 0

>> syms x;
>> p=4*x^3+4*x^2-2*x-2;
>> int(p)
ans =x^4 + (4*x^3)/3 - x^2 - 2*x

La función polyint calcula la integral cuando se expresa un polinomio como vector formado por los coeficientes

>> p=[4 4 -2 2];
>> polyint(p)
ans =    1.0000    1.3333   -1.0000    2.0000         0

Raíces de un polinomio

Cuando se expresa un polinomio de forma simbólica se utiliza la función solve

>> syms x;
>> p=x^5-3.5*x^4+2.75*x^3+2.125*x^2-3.875*x+1.25;
>> solve(p)
ans =
       2
      -1
     1/2
 i/2 + 1
 1 - i/2

Cuando se expresa un polinomio como vector formado por los coeficientes, se emplea la función roots.

>> p=[1 -3.5 2.75 2.125 -3.875 1.25];
>> roots(p)
ans =
   2.0000          
  -1.0000          
   1.0000 + 0.5000i
   1.0000 - 0.5000i
   0.5000   

Conocidas las raíces del polinomio podemos calcular el vector que guarda los coeficientes mediante poly

>> r=[2 -1 1+0.5i 1-0.5i 0.5]; %raíces del polinomio
>> poly(r)
ans =    1.0000   -3.5000    2.7500    2.1250   -3.8750    1.2500

Obtenemos el polinomio p a partir de sus raíces

Factorización

La función factor convierte un polinomio expresado en forma simbólica en factores

>> syms x;
>> p=x^3-6*x^2+11*x-6;
>> factor(p)
ans =(x - 3)*(x - 1)*(x - 2)

Expansión

La función expand realiza operaciones con polinomios, por ejemplo, devuelve el polinomio p a partir de sus factores

>> syms x;
>> p=(x - 3)*(x - 1)*(x - 2);
>> expand(p)
ans =x^3 - 6*x^2 + 11*x - 6
>> p=(x-1)^3+2*(x+3)^2+x^2-2*x-2;
>> expand(p) 
ans =x^3 + 13*x + 15

Fracciones polinómicas

La expansión de una fracción polinómica en fracciones más simples, [r,p,k]=residue(num,den) es una operación muy útil para las integrales de funciones racionales y las transformadas inversas de Laplace.

${\displaystyle \frac{A(x)}{B(x)}=\frac{a_1{x}^m+a_2{x}^{m-1}+\mathrm{....}+a_{m}x+a_{m+1}}{b_1{x}^n+b_2{x}^{n-1}+\mathrm{....}+b_{n}x+b_{n+1}}}$

Si m<n es una fracción propia y si m≥n se conoce como fracción impropia.Trataremos en primer lugar, las fracciones propias.

1.-Raíces reales distintas

Cuando las raíces son r₁, r₂,...r_n, son reales y distintas, expresamos el cociente como

${\displaystyle \frac{A(x)}{B(x)}=\frac{c_1}{x-r_1}+\frac{c_2}{x-r_2}+\mathrm{...}+\frac{c_n}{x-r_n}}$

Las constantes c₁, c₂,...c_n, se denominan residuos.

[c,r]=residue(a,b) calcula los residuos c y las raíces r de una fracción polinómica

${\displaystyle \frac{x-2}{x^3-x^2-6x}}$

>> a=[1 -2];
>> b=[1 -1 -6 0];
>> [c,r]=residue(a,b)
c =
    0.0667
   -0.4000
    0.3333
r =
     3
    -2
     0

${\displaystyle \frac{x-2}{x^3-x^2-6x}=\frac{0.0667}{x-3}+\frac{-0.4}{x-(-2)}+\frac{0.333}{x-0}}$

2.-Raíces complejas distintas

Si r es la raíz compleja de una ecuación, también es raíz su compleja conjugada r^*. Entonces el residuo c correpondiente a la raíz r es igual al conjugado c^* del residuo correpondiente a la raíz r^*.

${\displaystyle \frac{x^2-2x+1}{x^3+3x^2+4x+2}}$

>> a=[1 -2 1];
>> b=[1 3 4 2];
>> [c,r]=residue(a,b)
c =
  -1.5000 + 2.0000i
  -1.5000 - 2.0000i
   4.0000          
r =
  -1.0000 + 1.0000i
  -1.0000 - 1.0000i
  -1.0000       

${\displaystyle \frac{x^2-2x+1}{x^3+3x^2+4x+2}=\frac{-1.5+2i}{x-(-1+i)}+\frac{-1.5-2i}{x-(-1-i)}+\frac{4}{x-(-1)}}$

Para eliminar los números complejos, sumamos las dos primeras fracciones, que en general se expresan

${\displaystyle \begin{array}{l}\frac{c+di}{x-(a+bi)}+\frac{c-di}{x-(a-bi)}=\frac{c+di}{(x-a)-bi}+\frac{c-di}{(x-a)+bi}=\\ \frac{2(cx-ca-bd)}{{(x-a)}^2+b^2}\end{array}}$

Con c=-1.5, d=2, a=-1, b=1, obtenemos

${\displaystyle \frac{-1.5+2i}{x-(-1+i)}+\frac{-1.5-2i}{x-(-1-i)}=-\frac{3x+7}{{(x+1)}^2+1}}$

Finalmente,

${\displaystyle \frac{x^2-2x+1}{x^3+3x^2+4x+2}=-\frac{3x+7}{x^2+2x+2}+\frac{4}{x+1}}$

3.-Raíces repetidas

Supongamos que la raíz r₁ se ha repetido k veces y las otras raices serán r_k+1, r_k+2...r_n

${\displaystyle \frac{A(x)}{B(x)}=\frac{c_1}{(x-r_1)}+\frac{c_2}{{(x-r_1)}^2}+\mathrm{...}\frac{c_k}{{(x-r_1)}^k}+\frac{c_{k+1}}{(x-r_{k+1})}+\mathrm{...}\frac{c_n}{(x-r_n)}}$

Sea

${\displaystyle \frac{5x-1}{x^3-3x-2}}$

>> a=[5 -1];
>> b=[1 0 -3 -2]; 
>> [c,r]=residue(a,b)
c =
    1.0000
   -1.0000
    2.0000
r =
    2.0000
   -1.0000
   -1.0000

${\displaystyle \frac{5x-1}{x^3-3x-2}=\frac{1}{x-2}+\frac{-1}{x+1}+\frac{2}{{(x+1)}^2}}$

4.-Fracciones impropias

Si el grado m del polinomio A es mayor que el grado n del polinomio B (m≥n), entonces

${\displaystyle \frac{A(x)}{B(x)}=Q(x)+\frac{R(x)}{B(x)}}$

Donde Q(x) es un polinomio de grado m-n, y el resto R(x) es un polinomio de gardo inferior a n.

${\displaystyle \frac{x^2+2x+3}{x^2+x-6}}$

La función residue devuelve un tercer parámetro q que contiene los coeficientes del polinomio cociente

>> a=[1 2 3];
>> b=[1 1 -6];
>> [c,r,q]=residue(a,b)
c =
   -1.2000
    2.2000
r =
    -3
     2
q =
     1

${\displaystyle \frac{x^2+2x+3}{x^2+x-6}=1+\frac{-1.2}{x+3}+\frac{2.2}{x-2}}$

Recuperando la fracción polinómica original

La función residue nos permite recuperar la fracción original, tal como se muestra a continuación

>> c=[-1.2 2.2];
>> r=[-3 2];
>> q=[1];
>> [a b]=residue(c,r,q)
a =     1     2     3
b =     1     1    -6