Sea f(t) una función definida en el intervalo [0, ∞). La transformada de Laplace F(s) de f(t) se define:

${\displaystyle F(s)={\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-st}f(t)dt}}$

Transformada de Laplace de algunas funciones

1.-Transformada de Laplace de f(t)=1

${\displaystyle F(s)={\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-st}dt}=-{\frac{1}{s}{e}^{-st}|}_0^{\infty }=\frac{1}{s}(s>0)}$

>> ft=sym('1');
>> Fs=laplace(ft)
Fs =1/s

2.-Transformada de Laplace de f(t)=exp(at)

${\displaystyle F(s)={\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-st}{e}^{at}dt}={\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{(a-s)t}dt}={\frac{1}{a-s}{e}^{(a-s)t}|}_0^{\infty }=\frac{1}{s-a}(s>a)}$

>> syms a t;
>> ft=exp(a*t);
>> Fs=laplace(ft)
Fs =-1/(a - s)

Vamos a comprobar la propiedad de linealidad de la transformada de Laplace

${\displaystyle \begin{array}{l}g(t)=c_1{f}_1(t)+c_2{f}_2(t)\\ G(s)=c_1{F}_1(s)+c_2{F}_2(s)\end{array}}$

G(s) es la transformada de Laplace de g(t). F₁(s) y F₂(s) son las transformdas de Laplace de f₁(t) y f₂(t) respectivamente. Calculamos la transformada de Laplace de cosh(at)

${\displaystyle \begin{array}{l}g(t)=\cosh (at)=\frac{1}{2}\left(e^{at}+e^{-at}\right)\\ G(s)=\frac{1}{2}\left(\frac{1}{s-a}+\frac{1}{s+a}\right)=\frac{s}{s^2-a^2}\\ g(t)=\sinh (at)=\frac{1}{2}\left(e^{at}-e^{-at}\right)\\ G(s)=\frac{1}{2}\left(\frac{1}{s-a}-\frac{1}{s+a}\right)=\frac{a}{s^2-a^2}\end{array}}$

>> syms a t;
>> ft=cosh(a*t);
>> Fs=laplace(ft)
Fs =-s/(a^2 - s^2)
>> ft=sinh(a*t);
>> Fs=laplace(ft)
Fs =-a/(a^2 - s^2)

3. Transformada de Laplace de f(t)=exp(iωt)

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{i\omega t}{e}^{-st}dt=}{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-(s-i\omega )t}dt=}-\frac{1}{s-i\omega }{e^{-(s-i\omega )t}|}_0^{\infty }=\\ \frac{1}{s-i\omega }=\frac{s}{s^2+{\omega }^2}+i\frac{\omega }{s^2+{\omega }^2}\\ e^{i\omega t}=\cos (\omega t)+i\sin (\omega t)\\ f(t)=\cos (\omega t)F(s)=\frac{s}{s^2+{\omega }^2}\\ f(t)=\sin (\omega t)F(s)=\frac{\omega }{s^2+{\omega }^2}\end{array}}$

>> syms t w;
>> ft=cos(w*t);
>> Fs=laplace(ft)
Fs =s/(s^2 + w^2)
>> ft=sin(w*t);
>> Fs=laplace(ft)
Fs =w/(s^2 + w^2)

4.-Transformada de Laplace de f(t)=exp(at)·exp(iωt)=exp((a+iω)t)

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{(a+i\omega )t}{e}^{-st}dt=}\frac{1}{s-(a+i\omega )}=\\ \frac{1}{(s-a)-i\omega }=\frac{s-a}{{(s-a)}^2+{\omega }^2}+i\frac{\omega }{{(s-a)}^2+{\omega }^2}\\ e^{(a+i\omega )t}=e^{at}·e^{i\omega t}=e^{at}\left(\cos (\omega t)+i\sin (\omega t)\right)\\ f(t)=e^{at}\cos (\omega t)F(s)=\frac{s-a}{{(s-a)}^2+{\omega }^2}\\ f(t)=e^{at}\sin (\omega t)F(s)=\frac{\omega }{{(s-a)}^2+{\omega }^2}\end{array}}$

>> syms a w t;
>> ft=exp(a*t)*sin(w*t);
>> Fs=laplace(ft)
Fs =w/(w^2 + (a - s)^2)
>> ft=exp(a*t)*cos(w*t);
>> Fs=laplace(ft)
Fs =-(a - s)/(w^2 + (a - s)^2)

5.-Transformada de Laplace de f(t)=tⁿ

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}{t}^n{e}^{-st}dt=}{-\frac{1}{s}{e}^{-st}{t}^n|}_0^{\infty }+\frac{n}{s}{\displaystyle \underset{0}{\overset{\infty }{\int }}{t}^{n-1}{e}^{-st}dt=}\\ \frac{n}{s}\frac{n-1}{s}{\displaystyle \underset{0}{\overset{\infty }{\int }}{t}^{n-2}{e}^{-st}dt=}\mathrm{...}\frac{n}{s}\frac{n-1}{s}\mathrm{...}\frac{1}{s}{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-st}dt=}\frac{n!}{s^n}\frac{1}{s}=\frac{n!}{s^{n+1}}\end{array}}$

>> syms t n;
>> ft=t^n;
>> Fs=laplace(ft)
Fs =piecewise([-1 < Re(n), gamma(n + 1)/s^(n + 1)])
>> ft=t^6;
>> Fs=laplace(ft)
Fs =720/s^7

6.-Transformada de Laplace de f(t)=tⁿ·exp(at)

Como se puede fácilmente comprobar

${\displaystyle f(t)=e^{at}{t}^{n}F(s)=\frac{n!}{{(s-a)}^{n+1}}}$

>> syms t a;
>> ft=exp(a*t)*t^6;
>> Fs=laplace(ft)
Fs =-720/(a - s)^7 

En general, tendremos que

${\displaystyle F(s-a)={\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-(s-a)t}f(t)dt=}{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-st}\left(e^{at}f(t)\right)dt}}$

Función escalón

Sea u(t) la función escalón, o función de Heaviside, definida del siguiente modo

${\displaystyle u(t)=\{\begin{array}{l}1t\ge 0\\ 0t<0\end{array}}$

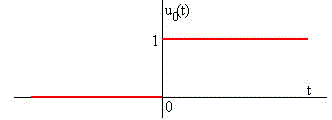
La función u(t-a), es una traslación a de la función escalón, se define de forma análoga

${\displaystyle u(t-a)=\{\begin{array}{l}1t\ge a\\ 0t<a\end{array}}$

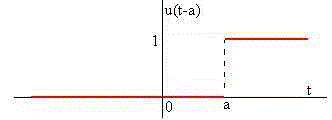
La transformada de Laplace de esta función es

${\displaystyle \underset{0}{\overset{\infty }{{\displaystyle \int }}}{e}^{-st}u(t-a)dt=\underset{a}{\overset{\infty }{{\displaystyle \int }}}{e}^{-st}dt=-\frac{1}{s}{e}^{-st}{|}_a^{\infty }=\frac{e^{-as}}{s}}$

>> syms t;
>> laplace(heaviside(t-2))
ans =exp(-2*s)/s
>> syms a positive;
>> laplace(heaviside(t-a))
ans =exp(-a*s)/s

Fijarse en la forma de obtener la transformda de Laplace de la la función Heaviside u(t-a), hay que especificar que a es una variable simbólica positiva, en caso contrario, no sabe calcular su transformada de Laplace.

La función escalón u(t-a) es importante para definir funciones por intervalos, como el pulso rectangular

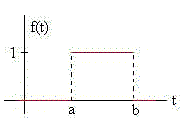
La función representada en la figura se escribe

${\displaystyle f(t)=u(t-a)-u(t-b)=\{\begin{array}{l}0t<a\\ 1a\le t\le b\\ 0t>b\end{array}}$

La transformada de Laplace de esta función es la diferencia

${\displaystyle F(s)=\frac{e^{-as}}{a}-\frac{e^{-bs}}{b}}$

Consideremos ahora, que la función f(t) es una sucesión de pulsos rectangulares, tal como se muestra en la figura

${\displaystyle f(t)={\displaystyle \sum _{n=0}^{\infty }\left\{u\left(t-2na\right)-u\left(t-(2n+1)a\right)\right\}}}$

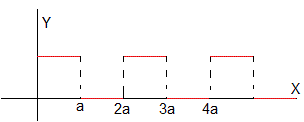
La transformada de Laplace es la suma

${\displaystyle \begin{array}{l}F(s)={\displaystyle \sum _{n=0}^{\infty }\left\{\frac{\exp (-2nas)}{s}-\frac{\exp (-(2n+1)as)}{s}\right\}}=\\ \frac{1-\exp (-as)}{s}{\displaystyle \sum _{n=0}^{\infty }{\left(\exp \left(-2as\right)\right)}^n}=\frac{1-\exp (-as)}{s}\frac{1}{1-\exp (-2as)}=\\ \frac{1-e^{-as}}{s\left(1-e^{-2as}\right)}\end{array}}$

Se ha utilizado la fórmula de la suma de los infinitos términos de una progresión geométrica cuyo primer término es 1 y la razón es exp(-2as)

La función u(t-a) cumple la siguiente propiedad

${\displaystyle \begin{array}{l}\underset{0}{\overset{\infty }{{\displaystyle \int }}}{e}^{-st}u(t-a)f(t-a)dt=\underset{a}{\overset{\infty }{{\displaystyle \int }}}{e}^{-st}f(t-a)dt=\\ \underset{0}{\overset{\infty }{{\displaystyle \int }}}{e}^{-s(\tau +a)}f(\tau )d\tau =e^{-as}\underset{0}{\overset{\infty }{{\displaystyle \int }}}{e}^{-s\tau }f(\tau )d\tau =e^{-as}\underset{0}{\overset{\infty }{{\displaystyle \int }}}{e}^{-st}f(t)dt=e^{-as}F(s)\end{array}}$

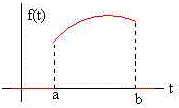
Sea la función f(t) cualesquiera que toma valores distintos de cero en el intervalo [a,b] se escribe

${\displaystyle \left(u(t-a)-u(t-b)\right)f(t)=\{\begin{array}{l}0t<a\\ f(t)a\le t\le b\\ 0t>b\end{array}}$

Consideremos la función

${\displaystyle \begin{array}{l}f(t)=\{\begin{array}{l}2t0<t<2\\ 42\le t\end{array}\\ f(t)=\left(u(t-0)-u(t-2)\right)(2t)+u(t-2)·4=\\ 2t-2(t-2)·u(t-2)t>0\end{array}}$

Cuya representación gráfica es

>> f=@(t) 2*t+2*(2-t).*heaviside(t-2);
>> fplot(f,[0,10])
>> ylim([0 5])

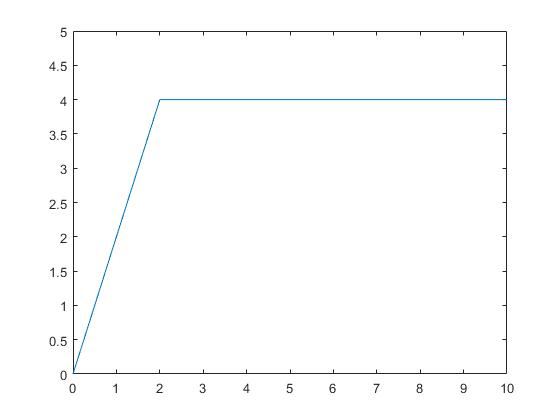
La transformada de Laplace de la función f(t) es

${\displaystyle F(s)=2\frac{1!}{s^2}-2e^{-2s}\frac{1!}{s^2}=\frac{2}{s^2}\left(1-e^{-2s}\right)}$

>> syms t;
>> ft=2*t+2*(2-t)*heaviside(t-2);
>> Fs=laplace(ft)
Fs =2/s^2 - 2/(s^2*exp(2*s))

8.-Transformada de Laplace de la función delta de Dirac, δ(t-a)

${\displaystyle \delta (t-a)=\{\begin{array}{l}\infty t=a\\ 0t\ne a\end{array}{\displaystyle \underset{0}{\overset{\infty }{\int }}\delta (t-a)dt}=1}$

Consideremos la función denominada impulso unidad, cuya área es la unidad

${\displaystyle \begin{array}{l}f(t)=\{\begin{array}{l}\frac{1}{k}a\le t\le a+k\\ 0t<at>a+k\end{array}\\ f(t)=\frac{1}{k}\left(u(t-a)-u(t-(a+k))\right)\end{array}}$

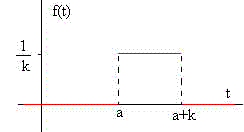
La transformada de Laplace de esta función es

${\displaystyle \begin{array}{l}F(s)=\frac{1}{k}\left(\frac{e^{-as}}{s}-\frac{e^{-(a+k)s}}{s}\right)=e^{-as}\frac{1-e^{-ks}}{ks}\\ \underset{k\to 0}{\lim }\left(\frac{1-e^{-ks}}{ks}\right)=\underset{k\to 0}{\lim }\left(\frac{s{e}^{-ks}}{s}\right)=\underset{k\to 0}{\lim }{e}^{-ks}=1\\ \underset{k\to 0}{\lim }f(t,a)=\delta (t-a)\\ \underset{k\to 0}{\lim F(s)}=e^{-as}\end{array}}$

Para calcular el límite cuando k tiende a cero en la segunda línea hemos aplicado la regla de L'Hôpital.

>> syms t a;
>> laplace(dirac(t-a))
ans =exp(-a*s)

Transformada de Laplace de una función periódica

Una función f(t) es periódica de periodo p, si cumple que f(t+p)=f(t). La función sin(t) es periódica de periodo 2π y la función sin(ωt) es periódica de periodo p=2π/ω.

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-st}f(t)dt}={\displaystyle \underset{0}{\overset{p}{\int }}{e}^{-st}f(t)dt}+{\displaystyle \underset{p}{\overset{2p}{\int }}{e}^{-st}f(t)dt}+{\displaystyle \underset{2p}{\overset{3p}{\int }}{e}^{-st}f(t)dt}+\mathrm{...}=\\ {\displaystyle \underset{0}{\overset{p}{\int }}{e}^{-st}f(t)dt}+{\displaystyle \underset{0}{\overset{p}{\int }}{e}^{-s(t+p)}f(t+p)dt}+{\displaystyle \underset{0}{\overset{p}{\int }}{e}^{-s(t+2p)}f(t+2p)dt}+\mathrm{...}=\\ {\displaystyle \underset{0}{\overset{p}{\int }}{e}^{-st}f(t)dt}+{\displaystyle \underset{0}{\overset{p}{\int }}{e}^{-s(t+p)}f(t)dt}+{\displaystyle \underset{0}{\overset{p}{\int }}{e}^{-s(t+2p)}f(t)dt}+\mathrm{...}=\\ {\displaystyle \underset{0}{\overset{p}{\int }}{e}^{-st}f(t)dt}+e^{-sp}{\displaystyle \underset{0}{\overset{p}{\int }}{e}^{-st}f(t)dt}+e^{-2sp}{\displaystyle \underset{0}{\overset{p}{\int }}{e}^{-st}f(t)dt}+\mathrm{...}=\\ \left(1+e^{-sp}+e^{-2sp}+e^{-3sp}+\mathrm{...}\right){\displaystyle \underset{0}{\overset{p}{\int }}{e}^{-st}f(t)dt}=\\ \frac{1}{1-e^{-sp}}{\displaystyle \underset{0}{\overset{p}{\int }}{e}^{-st}f(t)dt}\end{array}}$

Entre paréntesis tenemos la suma de infinitos términos de una progresión geométrica cuyo primer término es 1 y cuya razón es e^-sp.

${\displaystyle S_{\infty }=\frac{a_0}{1-r}=\frac{1}{1-e^{-sp}}}$

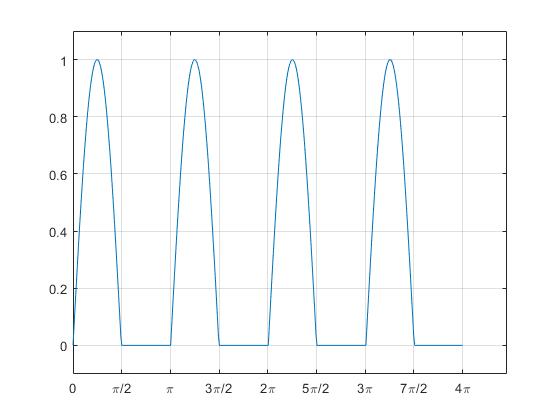
Calcular la transformada de Laplace de la función

${\displaystyle \begin{array}{l}f(t)=\{\begin{array}{l}\sin (\omega t)0\le t\le \pi /\omega \\ 0\pi /\omega <t<2\pi /\omega \end{array}\\ f(t)=f\left(t+\frac{2\pi }{\omega }\right)\\ F(s)=\frac{1}{1-e^{-sp}}{\displaystyle \underset{0}{\overset{p}{\int }}{e}^{-st}f(t)dt}=\frac{1}{1-e^{-2\pi s/\omega }}{\displaystyle \underset{0}{\overset{\pi /\omega }{\int }}{e}^{-st}\sin (\omega t)dt}\\ \frac{1}{1-e^{-2\pi s/\omega }}{\left(-e^{-st}\frac{\omega \cos (\omega t)+s\sin (\omega t)}{{\omega }^2+s^2}\right)|}_0^{\pi /\omega }=\frac{\omega }{\left({\omega }^2+s^2\right)\left(1-e^{-\pi s/\omega }\right)}\end{array}}$

Se ha integrado dos veces por partes exp(-st)·sin(ωt)

Tomando ω=2

t=linspace(0,pi,100);
x=sin(2*t).*(t>=0 & t<=pi/2);
t=linspace(0,4*pi,400);
xx=[x x x x]; %se repite la función cuatro veces
plot(t,xx)
ylim([-0.1 1.1])
set(gca,'xtick',0:pi/2:4*pi)
set(gca,'xticklabel',{'0','\pi/2','\pi','3\pi/2','2\pi','5\pi/2',
'3\pi','7\pi/2','4\pi'})
grid on

Calculamos la transformada de Laplace del siguiente modo:

>> syms pi s t w;
>> g=int(exp(-s*t)*sin(w*t),t,0,pi/w)/(1-exp(-2*pi*s/w))
g =-(w*(1/exp((pi*s)/w) + 1))/((s^2 + w^2)*(1/exp((2*pi*s)/w) - 1))
>> simplify(g)
ans =(w*exp((pi*s)/w))/((s^2 + w^2)*(exp((pi*s)/w) - 1))

Transformada de Laplace de derivadas e integrales

1.-Transformada de Laplace de una derivada

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}f\text{'}(t)e^{-st}dt=}{e^{-st}f(t)|}_0^{\infty }+s{\displaystyle \underset{0}{\overset{\infty }{\int }}f(t)e^{-st}dt=}s{\displaystyle \underset{0}{\overset{\infty }{\int }}f(t)e^{-st}dt-f(0)}\\ {\displaystyle \underset{0}{\overset{\infty }{\int }}f\text{'}\text{'}(t)e^{-st}dt=}s{\displaystyle \underset{0}{\overset{\infty }{\int }}f\text{'}(t)e^{-st}dt-f\text{'}(0)}=s\left(s{\displaystyle \underset{0}{\overset{\infty }{\int }}f(t)e^{-st}dt-f(0)}\right)-f(0)=\\ s^2{\displaystyle \underset{0}{\overset{\infty }{\int }}f(t)e^{-st}dt-s}f(0)-f\text{'}(0)\\ {\displaystyle \underset{0}{\overset{\infty }{\int }}{f}^{(n)}(t)e^{-st}dt=}{s}^n{\displaystyle \underset{0}{\overset{\infty }{\int }}f(t)e^{-st}dt-s^{n-1}}f(0)-s^{n-2}{f}^{(1)}(0)-f^{(n-1)}(0)\end{array}}$

Vamos a aplicar la transformada de Laplace a una ecuación diferencial con las condiciones iniciales especificadas. En la siguiente página aprenderemos a obtener la solución de la ecuación diferencial, aplicando la transformada inversa de Laplace.

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}+4\frac{dx}{dt}+3x=0t=0\{\begin{array}{l}x=3\\ \frac{dx}{dt}=1\end{array}\\ \left(s^{2}F(s)-sx(0)-x\text{'}(0)\right)+4\left(sF(s)-x(0)\right)+3F(s)=0\\ \left(s^{2}F(s)-3s-1\right)+4\left(sF(s)-3\right)+3F(s)=0\\ s^{2}F(s)+4sF(s)-3s-13+3F(s)=0\\ F(s)=\frac{3s+13}{s^2+4s+3}\end{array}}$

2.-Transformada de Laplace de una integral

Sea la función

${\displaystyle g(t)={\displaystyle \underset{0}{\overset{t}{\int }}f(\tau )d\tau }}$

La transformada de Laplace se calcula del siguiente modo

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-st}f(t)dt=}{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-st}g\text{'}(t)dt=}s{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-st}g(t)dt-g(0)}=s{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-st}g(t)dt}\\ {\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-st}g(t)dt=\frac{1}{s}}{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-st}f(t)dt}\end{array}}$

Comprobamos esta relación con el siguiente ejemplo

${\displaystyle \begin{array}{l}f(t)=\cos (\omega t)F(s)=\frac{s}{s^2+{\omega }^2}\\ g(t)={\displaystyle \underset{0}{\overset{t}{\int }}\cos (\omega t)dt=\frac{1}{\omega }}\sin (\omega t)G(s)=\frac{1}{s^2+{\omega }^2}\end{array}}$