Valores propios reales y distintos

Comencemos con un sistema de dos ecuaciones diferenciales, con las condiciones iniciales especificadas.

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{dx}{dt}=x+2y\\ \frac{dy}{dt}=3x+2y\end{array}\\ t=0\{\begin{array}{l}x=0\\ y=-4\end{array}\end{array}}$

Resolvemos el sistema de forma analítica

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=\frac{dx}{dt}+2\frac{dy}{dt}\\ \frac{d^{2}x}{d{t}^2}-\frac{dx}{dt}-2(3x+2y)=0\\ \frac{d^{2}x}{d{t}^2}-\frac{dx}{dt}-6x-4\frac{1}{2}\left(\frac{dx}{dt}-x\right)=0\\ \frac{d^{2}x}{d{t}^2}-3\frac{dx}{dt}-4x=0\\ s^2-3s-4=0\{\begin{array}{l}{s}_1=4\\ s_2=-1\end{array}\\ x=C_1{e}^{4t}+C_2{e}^{-t}\\ y=\frac{1}{2}\left(\frac{dx}{dt}-x\right)=\frac{3}{2}{C}_1{e}^{4t}-C_2{e}^{-t}\end{array}}$

Determinamos C₁ y C₂ a partir de las condiciones iniciales

${\displaystyle \begin{array}{l}\{\begin{array}{l}0=C_1+C_2\\ -4=\frac{3}{2}{C}_1-C_2\end{array}\\ x=\frac{8}{5}\left(-e^{4t}+e^{-t}\right)\\ y=-\frac{4}{5}\left(3e^{4t}+2e^{-t}\right)\end{array}}$

Resolvemos el sistema de las dos ecuaciones diferenciales utilizando la función dsolve de MATLAB

>> syms x y t;
>> eq1='Dx=x+2*y';
>> eq2='Dy=3*x+2*y';
>> [x1 y1]=dsolve(eq1,eq2,'x(0)=0','y(0)=-4')
x1 =8/(5*exp(t)) - (8*exp(4*t))/5
y1 =- 8/(5*exp(t)) - (12*exp(4*t))/5

Escribimos el sistema de dos ecuaciones diferenciales lineales en forma matricial

${\displaystyle \begin{array}{l}\left(\begin{array}{c}\frac{dx}{dt}\\ \frac{dy}{dt}\end{array}\right)=\left(\begin{array}{cc}1& 2\\ 3& 2\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\\ \dot{u}=Au\end{array}}$

Calculamos los valores y vectores propios de la matriz A mediante la función eig de MATLAB

>> A=sym('[1,2;3,2]');
>> [V D]=eig(A)
V =
[ -1, 2/3]
[  1,   1]
D =
[ -1, 0]
[  0, 4]

Los valores propios son λ₁=-1 y λ₂=4 y los correspondientes vectores propios son v₁=[-1, 2/3] y v₂=[1, 1]. La solución del sistema de ecuaciones diferenciales se escribe

${\displaystyle \begin{array}{l}x=C_1{v}_1{e}^{{\lambda }_{1}t}+C_2{v}_2{e}^{{\lambda }_{2}t}\\ \left(\begin{array}{c}x\\ y\end{array}\right)=C_1\left(\begin{array}{c}-1\\ 1\end{array}\right)e^{-t}+C_2\left(\begin{array}{c}2/3\\ 1\end{array}\right)e^{4t}\end{array}}$

Determinamos C₁ y C₂ a partir de las condiciones iniciales

${\displaystyle \begin{array}{l}\left(\begin{array}{c}0\\ -4\end{array}\right)=C_1\left(\begin{array}{c}-1\\ 1\end{array}\right)+C_2\left(\begin{array}{c}2/3\\ 1\end{array}\right)\{\begin{array}{l}{C}_1=-\frac{8}{5}\\ C_2=-\frac{12}{5}\end{array}\\ x=\frac{8}{5}\left(-e^{4t}+e^{-t}\right)\\ y=-\frac{4}{5}\left(3e^{4t}+2e^{-t}\right)\end{array}}$

Elaboramos un script para obtener la solución final de x denominada x(1) en el código y de y, denominada x(2) en funcion del tiempo t.

syms t;
A=sym('[1,2;3,2]');
[V D]=eig(A); %vectores propios y valores propios
x0=sym('[0;-4]'); %condiciones inciales
C=V\x0;  %coeficientes C1 y C2
C=C.*exp(diag(D)*t); %multiplica cada coeficiente por la exponencial
x=V*C;
x=simplify(x)

Corremos el script en la ventana de comandos y obtenemos el resultado para x y para y.

Valores propios complejos conjugados

Sea el sistema homogéneo de dos ecuaciones diferenciales lineales, con las condiciones iniciales especificadas

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{dx}{dt}=3x-13y\\ \frac{dy}{dt}=5x+y\end{array}\\ t=0\{\begin{array}{l}x=3\\ y=-10\end{array}\end{array}}$

Resolvemos este sistema con la función dsolve de MATLAB

>> syms x y t;
>> eq1='Dx=3*x-13*y';
>> eq2='Dy=5*x+y';
>> [x1 y1]=dsolve(eq1,eq2,'x(0)=3','y(0)=-10')
x1 =3*cos(8*t)*exp(2*t) + (133*sin(8*t)*exp(2*t))/8
y1 =(25*sin(8*t)*exp(2*t))/8 - 10*cos(8*t)*exp(2*t) 

Escribimos el sistema de dos ecuaciones diferenciales lineales en forma matricial

${\displaystyle \begin{array}{l}\left(\begin{array}{c}\frac{dx}{dt}\\ \frac{dy}{dt}\end{array}\right)=\left(\begin{array}{cc}3& -13\\ 5& 1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\\ \dot{u}=Au\end{array}}$

Calculamos los valores y vectores propios de la matriz A mediante la función eig de MATLAB

>> A=sym('[3,-13;5,1]')
>> [V D]=eig(A) 
V = 
[ 1/5 - (8*i)/5, (8*i)/5 + 1/5]
[             1,             1]
D =
[ 2 - 8*i,       0]
[       0, 8*i + 2] 

Los valores propios son λ₁=2-8i y λ₂=2+8i. y los correspondientes vectores propios son v₁=[(1-8i)/5, 1] y v₂=[(1+8i)/5, 1]. La solución del sistema de ecuaciones diferenciales se escribe

${\displaystyle \begin{array}{l}x=C_1{v}_1{e}^{{\lambda }_{1}t}+C_2{v}_2{e}^{{\lambda }_{2}t}\\ \left(\begin{array}{c}x\\ y\end{array}\right)=C_1\left(\begin{array}{c}\frac{1-8i}{5}\\ 1\end{array}\right)e^{(2-8i)t}+C_2\left(\begin{array}{c}\frac{1+8i}{5}\\ 1\end{array}\right)e^{(2+8i)t}\end{array}}$

Determinamos C₁ y C₂ con las condiciones iniciales

${\displaystyle \begin{array}{l}\left(\begin{array}{c}3\\ -10\end{array}\right)=C_1\left(\begin{array}{c}\frac{1-8i}{5}\\ 1\end{array}\right)+C_2\left(\begin{array}{c}\frac{1+8i}{5}\\ 1\end{array}\right)\{\begin{array}{l}{C}_1=\frac{-80+25i}{16}\\ C_2=-\frac{80+25i}{16}\end{array}\\ x=\frac{-80+25i}{16}·\frac{1-8i}{5}{e}^{(2-8i)t}-\frac{80+25i}{16}·\frac{1+8i}{5}{e}^{(2+8i)t}=\\ x=\frac{1}{8}{e}^{2t}\left(24\cos (8t)+\frac{133}{8}\sin (8t)\right)\\ y=\frac{-80+25i}{16}{e}^{(2-8i)t}-\frac{80+25i}{16}{e}^{(2+8i)t}=\\ y=\frac{5}{8}{e}^{2t}\left(-16\cos (8t)+5\sin (8t)\right)\end{array}}$

El cálculo de las expresiones de x e y en función del tiempo t es bastante largo. Podemos utilizar la función simplify de MATLAB para efectuar las operaciones con números complejos y simplificarla.

>> syms t;
>> x=(-80+25*i)*(1-8*i)*exp((2-8*i)*t)/80-(80+25*i)*(1+8*i)*exp((2+8*i)*t)/80;
>> simplify(x) 
ans =(exp(2*t)*(24*cos(8*t) + 133*sin(8*t)))/8
>> y=(-80+25*i)*exp((2-8*i)*t)/16-(80+25*i)*exp((2+8*i)*t)/16;
>> simplify(y)
ans =-(5*exp(2*t)*(16*cos(8*t) - 5*sin(8*t)))/8

Utilizamos el script anterior cambiando los valores de los elementos de la matriz A, y del vector x₀ de los valores iniciales, obtenemos el mismo resultado para x y para y

....
A=sym('[3,-13;5,1]');
x0=sym('[3;-10]'); %condiciones inciales
....

Valores propios reales repetidos

Sea el sistema homogéneo de dos ecuaciones diferenciales lineales, con las condiciones iniciales especificadas

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{dx}{dt}=7x+y\\ \frac{dy}{dt}=-4x+3y\end{array}\\ t=0\{\begin{array}{l}x=2\\ y=-5\end{array}\end{array}}$

Resolvemos el sistema de forma analítica

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=7\frac{dx}{dt}+\frac{dy}{dt}\\ \frac{d^{2}x}{d{t}^2}=7\frac{dx}{dt}+\left(-4x+3y\right)=7\frac{dx}{dt}-4x+3y\\ \frac{d^{2}x}{d{t}^2}=7\frac{dx}{dt}-4x+3\left(\frac{dx}{dt}-7x\right)\\ \frac{d^{2}x}{d{t}^2}-10\frac{dx}{dt}+25x=0\\ s^2-10s+25=0\{\begin{array}{l}{\lambda }_1=5\\ {\lambda }_2=5\end{array}\\ x=\left(C_1+C_{2}t\right)e^{5t}\\ y=\frac{dx}{dt}-7x=\left(C_2-2C_1-2C_{2}t\right)e^{5t}\end{array}}$

Determinamos C₁ y C₂ con las condiciones iniciales

${\displaystyle \begin{array}{l}\{\begin{array}{l}2=C_1\\ -5=C_2-2C_1\end{array}\\ C_1=2C_2=-1\\ x=\left(2-t\right)e^{5t}\\ y=\left(-5+2t\right)e^{5t}\end{array}}$

Intentamos resolver este sistema con la función dsolve de MATLAB

>> syms x y t;
>> eq1='Dx=7*x+y';
>> eq2='Dx=-4*x+3*y';
>> [x1 y1]=dsolve(eq1,eq2,'x(0)=2','y(0)=-5')
Warning: more equations than unknowns: trying heuristics to reduce 
to square system [ode::solve_intern] 

Obtenemos un aviso Warning y no aparece la solución analítica

Escribimos el sistema de las dos ecuaciones diferenciales lineales en forma matricial

${\displaystyle \begin{array}{l}\left(\begin{array}{c}\frac{dx}{dt}\\ \frac{dy}{dt}\end{array}\right)=\left(\begin{array}{cc}7& 1\\ -4& 3\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\\ \dot{u}=Au\end{array}}$

Calculamos los valores y vectores propios de la matriz A mediante la función eig de MATLAB

>> A=sym('[7,1;-4,3]');
>> [V D]=eig(A)
V =
 -1/2
    1
D =
[ 5, 0]
[ 0, 5]

Los valores propios son λ₁=5 y λ₂=5, repetidos y el correspondiente vector propio son v₁=[-1/2, 1] . La solución del sistema de ecuaciones diferenciales se escribe

${\displaystyle x=C_1{v}_1{e}^{\lambda t}+C_2\left(t{v}_1+v_2\right)e^{\lambda t}}$

El vector v₂ se calcula del siguiente modo:

${\displaystyle \begin{array}{l}({\rm A}-\lambda I)v_2=v_1\\ \left(\begin{array}{cc}7& 1\\ -4& 3\end{array}\right)-5\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)=\left(\begin{array}{cc}2& 1\\ -4& -2\end{array}\right)\\ \left(\begin{array}{cc}2& 1\\ -4& -2\end{array}\right)\left(\begin{array}{c}{v}_{2x}\\ v_{2y}\end{array}\right)=\left(\begin{array}{c}-1/2\\ 1\end{array}\right)\end{array}}$

obtenemos la misma ecuación, una relación entre las dos componentes del vector v₂, 2v_2x+v_2y=-1/2. Un posible vector sería v₂=[0 -1/2].

Determinamos C₁ y C₂ con las condiciones iniciales

${\displaystyle \begin{array}{l}\left(\begin{array}{c}x\\ y\end{array}\right)=C_1\left(\begin{array}{c}-1/2\\ 1\end{array}\right)e^{5t}+C_2\left(t\left(\begin{array}{c}-1/2\\ 1\end{array}\right)+\left(\begin{array}{c}0\\ -1/2\end{array}\right)\right)e^{5t}\\ \left(\begin{array}{c}2\\ -5\end{array}\right)=C_1\left(\begin{array}{c}-1/2\\ 1\end{array}\right)+C_2\left(\begin{array}{c}0\\ -1/2\end{array}\right)\{\begin{array}{l}{C}_1=-4\\ C_2=2\end{array}\\ \left(\begin{array}{c}x\\ y\end{array}\right)=-4\left(\begin{array}{c}-1/2\\ 1\end{array}\right)e^{5t}+2\left(t\left(\begin{array}{c}-1/2\\ 1\end{array}\right)+\left(\begin{array}{c}0\\ -1/2\end{array}\right)\right)e^{5t}\\ x=(2-t)e^{5t}\\ y=(-5+2t)e^{5t}\end{array}}$

Los casos de raíces repetidas tres veces o más han de ser estudiados cuidadosamente, remitimos a la segunda referencia al final de esta página.

Ejemplos

Oscilaciones amortiguadas

Sea la ecuación diferencial de segundo orden que describe un oscilador amortiguado

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}+4\frac{dx}{dt}+68x=0\\ s^2+4s+68=0\{\begin{array}{l}{s}_1=-2+8i\\ s_2=-2-8i\end{array}\\ x=C_1{e}^{(-2+8i)t}+C_2{e}^{(-2-8i)t}\end{array}}$

Escribimos la ecuación diferencial de segundo orden en forma de sistema de dos ecuaciones diferenciales de primer orden y en forma matricial

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{dx}{dt}=y\\ \frac{dy}{dt}=-68x-4y\end{array}\\ \left(\begin{array}{c}\frac{dx}{dt}\\ \frac{dy}{dt}\end{array}\right)=\left(\begin{array}{cc}0& 1\\ -68& -4\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\end{array}}$

Calculamos los valores y vectores propios de la matriz A mediante la función eig de MATLAB

>> A=sym('[0,1;-68,-4]');
>> [V D]=eig(A)
V =
[ (2*i)/17 - 1/34, - (2*i)/17 - 1/34]
[               1,                 1]
D =
[ - 8*i - 2,       0]
[         0, 8*i - 2]

Los valores propios son λ₁=-2-8i y λ₂=-2+8i. y los correspondientes vectores propios son v₁=[(-1+4i)/34, 1] y v₂=[(-1-4i)/34, 1], o mejor, v₁=[1, (-2-8i)] y v₂=[1, (-2+8i)].

La solución del sistema de ecuaciones diferenciales se escribe

${\displaystyle \begin{array}{l}x=C_1{v}_1{e}^{{\lambda }_{1}t}+C_2{v}_2{e}^{{\lambda }_{2}t}\\ \left(\begin{array}{c}x\\ y\end{array}\right)=C_1\left(\begin{array}{c}1\\ -2-8i\end{array}\right)e^{(-2-8i)t}+C_2\left(\begin{array}{c}1\\ -2+8i\end{array}\right)e^{(-2+8i)t}\\ x=C_1{e}^{(-2-8i)t}+C_2{e}^{(-2+8i)t}\\ y=(-2-8i)C_1{e}^{(-2-8i)t}+(-2+8i)C_2{e}^{(-2+8i)t}\end{array}}$

Dadas las condiciones iniciales, posición y velocidad inicial, calculamos las constantes C₁ y C₂.

${\displaystyle \begin{array}{l}t=0\{\begin{array}{l}x=1\\ \frac{dx}{dt}=y=0\end{array}\\ C_1=\frac{4+i}{8}{C}_2=\frac{4-i}{8}\end{array}}$

Obtenemos las expresiones de x e y realizando las siguientes operaciones en la ventana de comandos

>> syms t;
>> x=(4+i)*exp((-2-8*i)*t)/8+(4-i)*exp((-2+8*i)*t)/8;
>> simplify(x)
ans =(4*cos(8*t) + sin(8*t))/(4*exp(2*t))
>> y=(-2-8*i)*(4+i)*exp((-2-8*i)*t)/8+(-2+8*i)*(4-i)*exp((-2+8*i)*t)/8; 
>> simplify(y)
ans =-(17*sin(8*t))/(2*exp(2*t))

Utilizamos el primer script cambiando los valores de los elementos de la matriz A y del vector x₀ de los valores iniciales, obtenemos la expresión de x y de y=dx/dt en función del tiempo.

....
A=sym('[3,-13;5,1]');
x0=sym('[1;0]'); %condiciones inciales
....

Corremos el script modificado en la ventana de comandos

Resultado
ans =
 (4*cos(8*t) + sin(8*t))/(4*exp(2*t))
          -(17*sin(8*t))/(2*exp(2*t))

Series de desintegración radioactiva

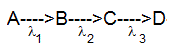
Sea una sustancia radioactiva A que al desintegrarse produce una sustancia radioactiva B, que al desintegrarse produce otra sustancia radioactiva C, que al desintegrarse da lugar a una sustancia estable D. El primer proceso A--->B de la serie está caracterizado por la constante λ₁, el segundo B--->C, por la constante λ₂ y el tercero C--->D, por la constante λ₃, tal como se ve en la figura. Las ecuaciones diferenciales que describen la variación con el tiempo t del número de núcleos de la sustancia A, x₁, de la sustancia B, x₂, de la sustancia C, x₃ y de la sustancia estable D, x₄ son

${\displaystyle \begin{array}{l}\frac{d{x}_1}{dt}=-{\lambda }_1{x}_1\\ \frac{d{x}_2}{dt}={\lambda }_1{x}_1-{\lambda }_2{x}_2\\ \frac{d{x}_3}{dt}={\lambda }_2{x}_2-{\lambda }_3{x}_3\\ \frac{d{x}_4}{dt}={\lambda }_3{x}_3\end{array}}$

Resolveremos el sistema de cuatro ecuaciones diferenciales con las siguientes condiciones iniciales: en el instante t=0, el número de núcleos de A es x₁=x₁₀, el de B es x₂=0, el de C, x₃=0, y el de D, x₄=0

Escribimos el sistema de ecuaciones diferenciales de forma matricial y supondremos que λ₁≠λ₂≠λ₃

${\displaystyle \left(\begin{array}{c}\frac{d{x}_1}{dt}\\ \frac{d{x}_2}{dt}\\ \frac{d{x}_3}{dt}\\ \frac{d{x}_4}{dt}\end{array}\right)=\left(\begin{array}{cccc}-{\lambda }_1& 0& 0& 0\\ {\lambda }_1& -{\lambda }_2& 0& 0\\ 0& {\lambda }_2& -{\lambda }_3& 0\\ 0& 0& {\lambda }_3& 0\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right)}$

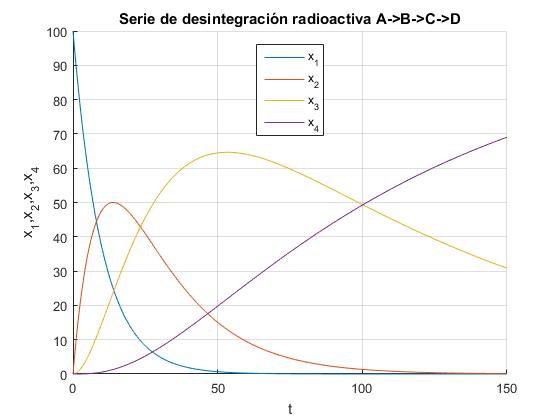
Elaboramos un script para hallar la solución del sistema de ecuaciones diferenciales y representar x₁, x₂, x₃ y x₄ en función del tiempo t

syms k1 k2 k3 t;
A=[-k1,0,0,0;k1,-k2,0,0;0,k2,-k3,0;0,0,k3,0];
A=subs(A,{k1,k2,k3},{0.1,0.05,0.01}); 
[V,D]=eig(A); %valores propios y vectores propios
x0=[100;0;0;0];  % condiciones iniciales
C=V\x0;  %coeficientes 
C=C.*exp(diag(D)*t);
x=V*C;
disp('Resultado')
x=simplify(x)
%gráfica
hold on
for i=1: length(x)
    ezplot(x(i),[0,150]);
end
ylim([0,100])
legend('x_1','x_2','x_3','x_4', 'location','north')
hold off
grid on
xlabel('t')
ylabel('x_1,x_2,x_3,x_4')
title('Serie de desintegración radioactiva A->B->C->D')

x =
                                                  100*exp(-t/10)
                                  200*exp(-t/10)*(exp(t/20) - 1)
     (1000*exp(-t/10))/9 - 250*exp(-t/20) + (1250*exp(-t/100))/9
 50*exp(-t/20) - (100*exp(-t/10))/9 - (1250*exp(-t/100))/9 + 100

Obtenemos el mismo resultado, resolviendo el sistema de cuatro ecuaciones diferenciales con dsolve

syms x1 x2 x3 x4 t;
eq1='Dx1=-0.1*x1';
eq2='Dx2=0.1*x1-0.05*x2';
eq3='Dx3=0.05*x2-0.01*x3';
eq4='Dx4=0.01*x3';
[x1,x2,x3,x4]=dsolve(eq1,eq2,eq3,eq4,'x1(0)=100','x2(0)=0','x3(0)=0'
,'x4(0)=0')

Oscilaciones de tres partículas

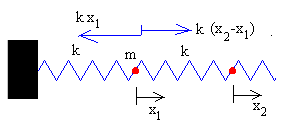
Vamos a estudiar un sistema formado por tres partículas de la misma masa m unidas por muelles elásticos iguales de constante k, tal como se muestra en la figura.

Supongamos que la primera partícula se desplaza x₁ de la posición de equilibrio, que la segunda se desplaza x₂ y la tercera, se desplaza x_3.

En las figuras, se muestra las fuerzas sobre cada una de las partículas

	Ecuación del movimiento de la primera partícula ${\displaystyle m\frac{d^2{x}_1}{d{t}^2}=-k{x}_1+k(x_2-x_1)}$
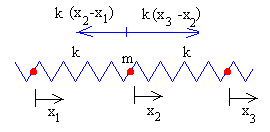	Ecuación del movimiento de la segunda partícula ${\displaystyle m\frac{d^2{x}_2}{d{t}^2}=-k(x_2-x_1)+k(x_3-x_2)}$
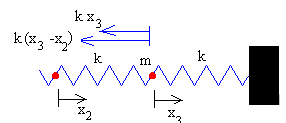	Ecuación del movimiento de la tercera partícula ${\displaystyle m\frac{d^2{x}_3}{d{t}^2}=-k(x_3-x_2)-k{x}_3}$

Para simplificar la notación, escribimos el cociente k/m como k, el sistema de tres ecuaciones diferenciales de segundo orden se puede convertir en un sistema homogéneo de seis ecuaciones diferenciales de primer orden cuya representación matricial es la siguinte:

${\displaystyle \begin{array}{l}\frac{d{x}_1}{dt}=y_1\frac{d{y}_1}{dt}=-2k{x}_1+k{x}_2\\ \frac{d{x}_2}{dt}=y_2\frac{d{y}_2}{dt}=k{x}_1-2k{x}_2+k{x}_3\\ \frac{d{x}_3}{dt}=y_3\frac{d{y}_3}{dt}=k{x}_2-2k{x}_3\\ \left(\begin{array}{c}\frac{d{x}_1}{dt}\\ \frac{d{y}_1}{dt}\\ \frac{d{x}_2}{dt}\\ \frac{d{y}_2}{dt}\\ \frac{d{x}_3}{dt}\\ \frac{d{y}_3}{dt}\end{array}\right)=\left(\begin{array}{cccccc}0& 1& 0& 0& 0& 0\\ -2k& 0& k& 0& 0& 0\\ 0& 0& 0& 1& 0& 0\\ k& 0& -2k& 0& k& 0\\ 0& 0& 0& 0& 0& 1\\ 0& 0& k& 0& -2k& 0\end{array}\right)\left(\begin{array}{c}{x}_1\\ y_1\\ x_2\\ y_2\\ x_3\\ y_3\end{array}\right)\end{array}}$

Calculamos los valores y vectores propios de la matriz A mediante la función eig de MATLAB

>> syms k;
>> A=[0,1,0,0,0,0;-2*k,0,k,0,0,0;0,0,0,1,0,0;k,0,-2*k,0,k,0;0,0,0,0,0,1
;0,0,k,0,-2*k,0];
>> [V D]=eig(A)
 V =...
 D=...

Podemos observar que los valores propios se corresponden con las frecuencias de los modos normales de vibración. La solución de este sistema de ecuaciones diferenciales se escribe

${\displaystyle \begin{array}{l}x={\displaystyle \sum _{i=1}^6{C}_i{v}_i{e}^{{\lambda }_{i}t}}\\ {\lambda }_1=-\sqrt{k\left(2-\sqrt{2}\right)}i{\lambda }_2=\sqrt{k\left(2-\sqrt{2}\right)}i\\ {\lambda }_3=\sqrt{k\left(2+\sqrt{2}\right)}i{\lambda }_4=-\sqrt{k\left(2+\sqrt{2}\right)}i\\ {\lambda }_5=\sqrt{2k}i{\lambda }_6=-\sqrt{2k}i\end{array}}$

v_i es el vector propio correspondiente al valor propio λ_i. Dadas las condiciones iniciales, posición y velocidad inicial de cada una de las tres partículas, calculamos las constantes C₁... C₆ y obtenemos la expresión de la posición y velocidad de cada una de las partículas en función del tiempo.

Las condiciones iniciales las especificamos en un vector x₀, que tiene seis elementos: [x₀₁,v₀₁,x₀₂,v₀₂,x₀₃,v₀₃]. x_i significa posición inicial y v_i velocidad incicial de la partícula i.

Creamos un script para resolver este problema y representar x₁, x₂ y x₃ en función del tiempo t. Se sugiere probar con otras condicions iniciales, por ejemplo.

${\displaystyle \begin{array}{l}{x}_{01}=1x_{02}=\sqrt{2}{x}_{03}=1\\ x_{01}=1x_{02}=0x_{03}=-1\\ x_{01}=1x_{02}=-\sqrt{2}{x}_{03}=1\end{array}}$

syms k t;
A=[0,1,0,0,0,0;-2*k,0,k,0,0,0;0,0,0,1,0,0;k,0,-2*k,0,k,0;0,0,0,0,0,1;
0,0,k,0,-2*k,0];
%para cambiar el valor de k/m, es distinto a subs(A,k,1)
A=subs(A,k,sym('1')); 
[V D]=eig(A); %valores propios y vectores propios
x0=sym('[1;0;0;0;-1;0]');  %para cambiar las condiciones iniciales
%x0=sym('[1;0;sqrt(2);0;1;0]');  %para cambiar las condiciones iniciales
C=V\x0;  %coeficientes C1 y C2
C=C.*exp(diag(D)*t); %multiplica cada coeficiente por la exp
x=V*C;
disp('Resultado')
x=simplify(x)
%gráfica
hold on
ezplot(x(1));
ezplot(x(3));
ezplot(x(5));
hold off
grid on
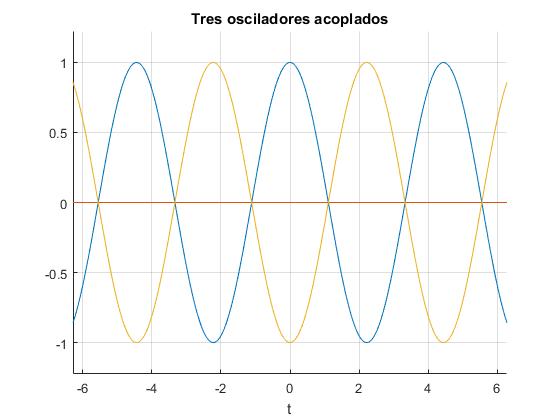
title('Tres osciladores acoplados')

Corremos el script en la ventana de comandos

Resultado
x = 
          cos(2^(1/2)*t)
 -2^(1/2)*sin(2^(1/2)*t)
                       0
                       0
         -cos(2^(1/2)*t)
  2^(1/2)*sin(2^(1/2)*t)

En este modo normal de oscilación las ecuaciones del movimiento de cada partícula son:

${\displaystyle \begin{array}{l}{x}_1=\cos \left(\sqrt{2}t\right)\\ x_2=0\\ x_3=-\cos \left(\sqrt{2}t\right)\end{array}}$

La segunda partícula permanece en reposo, tal como podemos apreciar en la figura: en rojo, la primera partícula, en azul, la segunda y en negro, la tercera.

Referencias

Paul Dawkins. Differential equations.

Steven J. Desjardins, Rémi Vaillancourt. Ordinary differential equations. Laplace transforms and Numerical methods for engineers.. University of Ottawa (2011). www.site.uottawa.ca/~remi/ode.pdf.

Barenkov, Demidovich, Efimenko...Problemas y ejercicios de Análisis Matemático. Paraninfo (1975)